14.1E: Exercícios para a Seção 14.1

Last updated
Save as PDF

Page ID: 187983

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para os exercícios a seguir, avalie cada função nos valores indicados.

1)$ W(x,y)=4x^2+y^2.$ Encontre$ W(2,−1), W(−3,6)$.

Resposta: $ W(2,−1) = 17,\quad W(−3,6) = 72$

2)$ W(x,y)=4x^2+y^2$. Encontre$ W(2+h,3+h).$

3) O volume de um cilindro circular reto é calculado por uma função de duas variáveis,$ V(x,y)=πx^2y,$ onde$ x$ é o raio do cilindro circular direito e$ y$ representa a altura do cilindro. Avalie$ V(2,5)$ e explique o que isso significa.

Resposta: $ V(2,5) = 20π\,\text{units}^3$Esse é o volume quando o raio é$ 2$ e a altura é$ 5$.

4) Um tanque de oxigênio é construído com um cilindro direito de altura$ y$ e raio$ x$ com dois hemisférios de raio$ x$ montados na parte superior e inferior do cilindro. Expresse o volume do cilindro em função de duas variáveis$ x$ e$ y$ encontre$ V(10,2)$ e explique o que isso significa.

Para os exercícios 5 a 10, encontre o domínio e o alcance da função dada. Indique o domínio na notação do construtor de conjuntos e o intervalo na notação de intervalo.

5)$ V(x,y)=4x^2+y^2$

Resposta: Domínio:$\big\{(x, y) \, | \, x \in \rm I\!R, y \in \rm I\!R\big\}$ Ou seja, todos os pontos na
faixa$xy$ -plane:$ [0, \infty) $

6)$ f(x,y)=\sqrt{x^2+y^2−4}$

Resposta: Domínio:$ \big\{(x, y) \, | \, x^2+y^2 \ge 4\big\}$
Alcance:$ [0, \infty) $

7)$ f(x,y)=4\ln(y^2−x)$

Resposta: Domínio:$ \big\{(x, y) \, | \, x<y^2 \big\}$
Alcance:$ (-\infty, \infty) $

8)$ g(x,y)=\sqrt{16−4x^2−y^2}$

Resposta: Domínio:$ \big\{(x, y) \, | \, \dfrac{x^2}{4} + \dfrac{y^2}{16} \le 1\big\}$
Alcance:$ [0, 4] $

9)$ z=\arccos(y−x)$

Resposta: Domínio:$ \big\{(x, y) \, | \, x - 1 \le y \le x + 1\big\}$ Ou seja, todos os pontos entre os gráficos de$y = x -1$$y = x +1 $ e.
Alcance:$ [0, \pi] $

10)$ f(x,y)=\dfrac{y+2}{x^2}$

Resposta: Domínio:$ \big\{(x, y) \, | \, x\neq 0 \big\}$
Alcance:$ (-\infty, \infty) $

Encontre a variedade das funções.

11)$ g(x,y)=\sqrt{16−4x^2−y^2}$

Resposta: $ \big\{z \, | \, 0≤z≤4\big\}$ou em notação de intervalo:$[0,4]$

12)$ V(x,y)=4x^2+y^2$

13)$ z=y^2−x^2$

Resposta: O conjunto$\rm I\!R$

Nos exercícios 14 a 29, encontre as curvas de nível de cada função nos valores indicados de$ c$ para visualizar a função dada. Esboce um gráfico de contorno para os exercícios em que são solicitados mais de 3 valores de$c$.

14)$ z(x,y)=y^2−x^2, \quad c=1$

15)$ z(x,y)=y^2−x^2,\quad c=4$

Resposta: $ y^2−x^2=4,$uma hipérbole

16)$ g(x,y)=x^2+y^2;\quad c=0, 1, 2, 3, 4, 9$

17)$ g(x,y)=4−x−y;\quad c=0,1, 2, 3, 4$

Resposta: As curvas de nível são linhas com$ y = -x + (4 - c) $.
Para cada valor,$c$ eles são:
$ c = 0: \, y = -x + 4$,
$ c = 1: \, y = -x + 3$,
$ c = 2: \, y = -x + 2$,
$ c = 3: \, y = -x + 1$,
$ c = 4: \, y = -x $.
O gráfico de contorno consiste em uma série de linhas paralelas.
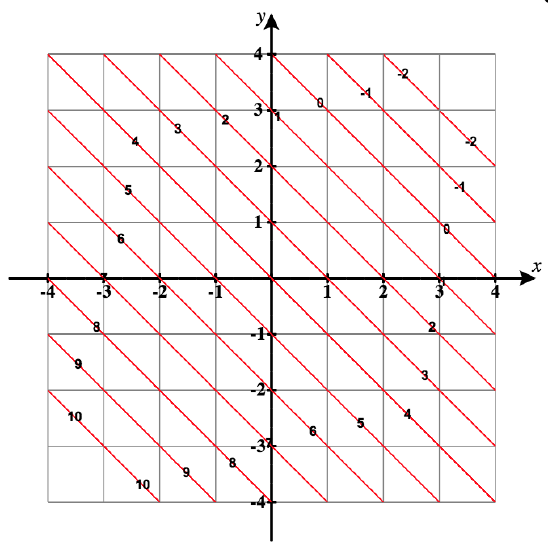
$Gráfico de contorno da função g (x, y) =4−x−y$

18)$ f(x,y)=xy;c=1;\quad c=−1$

19)$ h(x,y)=2x−y;\quad c=-2,0,2$

Resposta: $ 2x−y=0,2x−y=−2,2x−y=2;$três linhas

20)$ f(x,y)=x^2−y;\quad c=1,2$

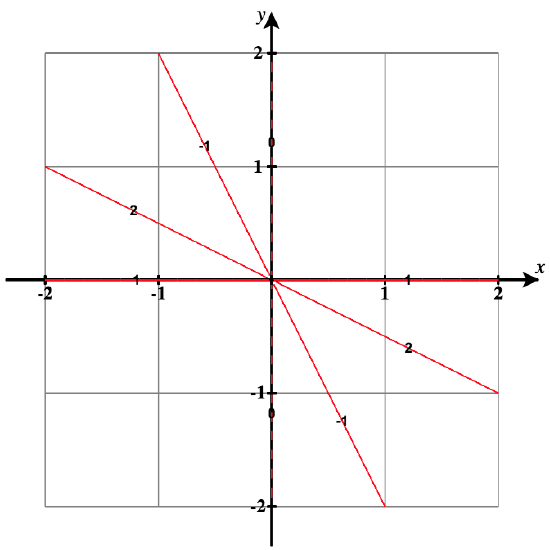
21)$ g(x,y)=\dfrac{x}{x+y};c=−1,0,1,2$

Resposta: As curvas de nível são linhas com a forma$ y = x \left( \dfrac{1-c}{c} \right) $. Em$c = 0$, resolvemos isso diretamente da equação$\dfrac{x}{x+y}=0$ para obter$x = 0$.
Para cada valor,$c$ eles são:
$ c = -1: \, y = -2x$,
$ c = 0: \, x = 0,\text{ with }y \ne 0$,
$ c = 1: \, y = 0,\text{ with }x \ne 0$,
$ c = 2: \, y = -\frac{1}{2}x$.
$Gráfico de contorno da função g (x, y) = x/ (x+y)$

22)$ g(x,y)=x^3−y;\quad c=−1,0,2$

23)$ g(x,y)=e^{xy};\quad c=\frac{1}{2},3$

Resposta: As curvas de nível têm a forma,$ y = \dfrac{\ln c}{x}$.
Para cada valor,$c$ eles são:
$ c = \frac{1}{2}: \, y = \dfrac{\ln \frac{1}{2}}{x}$ que podem ser reescritos como,$y = -\dfrac{\ln 2}{x}$

$ c = 3: \, y = \dfrac{\ln 3}{x}$.

24)$ f(x,y)=x^2;\quad c=4,9$

25)$ f(x,y)=xy−x;\quad c=−2,0,2$

Resposta: As curvas de nível têm a forma:$ y = \dfrac{c}{x} + 1$.
Aqui$y = \dfrac{-2}{x} + 1,\quad y = 1,\quad y = \dfrac{2}{x} + 1$ ou$ xy−x=−2,\,xy−x=0,\,xy−x=2$

26)$ h(x,y)=\ln(x^2+y^2);\quad c=−1,0,1$

27)$ g(x,y)=\ln\left(\dfrac{y}{x^2}\right);\quad c=−2,0,2$

Resposta: As curvas de nível têm a forma,$ y =e^c x^2$.
Para cada valor,$c$ eles são:
$ c = -2: \, y = e^{-2} x^2 $,
$ c = 0: \, y = x^2 $,
$ c = 2: \, y = e^{2} x^2 $.

28)$ z=f(x,y)=\sqrt{x^2+y^2},\quad c=3$

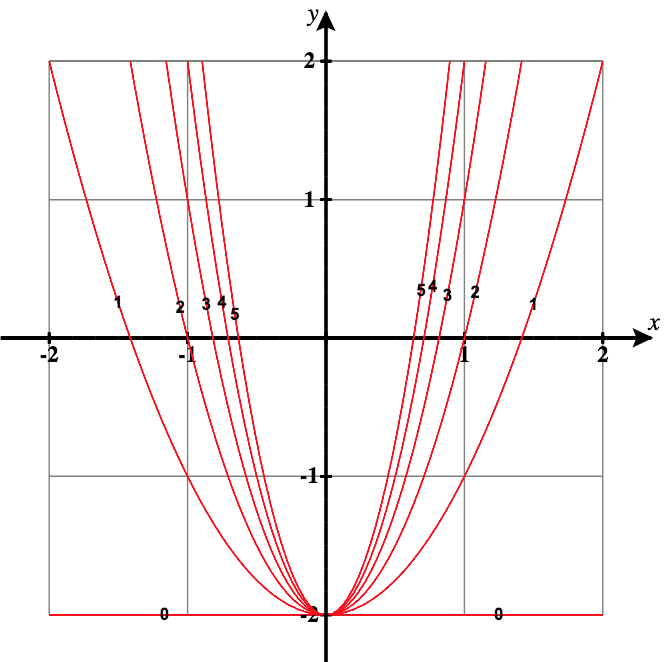
29)$ f(x,y)=\dfrac{y+2}{x^2},\quad c=$ qualquer constante

Resposta: As curvas de nível são parábolas do formulário$ y=cx^2−2,\text{ with }x \ne 0$.
$Gráfico de contorno da função f (x, y) = (y + 2) /x^2$

Nos exercícios 30-32, encontre os traços verticais das funções nos valores indicados de$ x$ e e$ y$ e plote os traços.

30)$ z=4−x−y, \quad x=2$

31)$ f(x,y)=3x+y^3, \quad x=1$

Resposta

$ z=3+y^3,$uma curva no $zy$plano -com regras paralelas ao$x$ eixo -

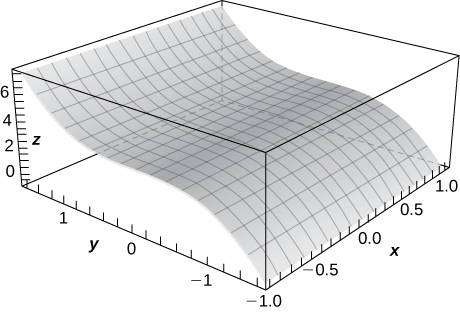
$Gráfico de superfície da função f (x, y) =3x+y^3$

32)$ z=\cos\sqrt{x^2+y^2}, \quad x=1$

Nos exercícios 33 a 38, encontre o domínio e o alcance de cada função.

33)$ z=\sqrt{100−4x^2−25y^2}$

Resposta: Domínio:$ \big\{(x, y) \, | \, \dfrac{x^2}{25}+\dfrac{y^2}{4}≤1\big\}$
Alcance:$ [0, 10] $

34)$ z=\ln(x−y^2)$

(35)$ f(x,y,z)=\dfrac{1}{\sqrt{36−4x^2−9y^2−z^2}}$

Resposta: Domínio:$ \big\{(x, y, z) \, | \, \dfrac{x^2}{9}+\dfrac{y^2}{4}+\dfrac{z^2}{36}<1\big\}$
Alcance:$ \big[\frac{1}{6}, \infty\big) $

36)$ f(x,y,z)=\sqrt{49−x^2−y^2−z^2}$

37)$ f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}$

Resposta: Domínio: Todos os pontos em$ xyz$ -space
Intervalo:$ \big(-\infty, \sqrt[3]{16}\,\big] $

38)$ f(x,y)=\cos\sqrt{x^2+y^2}$

Nos exercícios 39 a 40, desenhe um gráfico da função.

39)$ z=f(x,y)=\sqrt{x^2+y^2}$

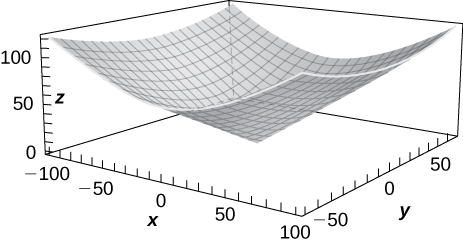
Resposta: $Gráfico de superfície da superfície f (x, y) =sqrt (x^2+y^2)$

40)$ z=x^2+y^2$

41) Use a tecnologia para representar graficamente$ z=x^2y.$

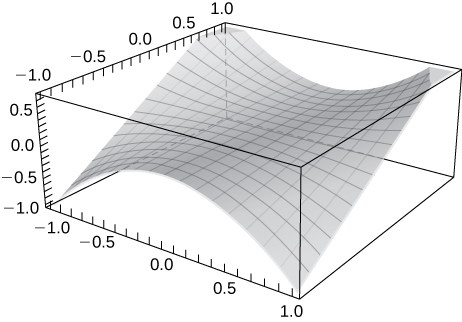
Resposta: $Gráfico de superfície da função z=x^2y$

Nos exercícios 42 a 46, esboce a função encontrando suas curvas de nível. Verifique o gráfico usando tecnologia, como CalcPlot3d.

(42)$ f(x,y)=\sqrt{4−x^2−y^2}$

43)$ f(x,y)=2−\sqrt{x^2+y^2}$

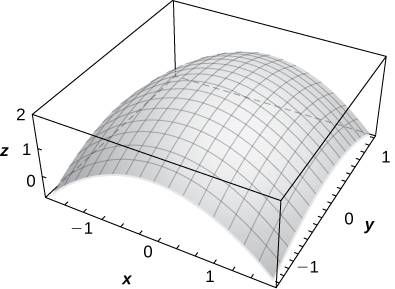
Resposta: $Gráfico de superfície da função f (x, y) =2−sqrt (x^2+y^2)$

44)$ z=1+e^{−x^2−y^2}$

45)$ z=\cos\sqrt{x^2+y^2}$

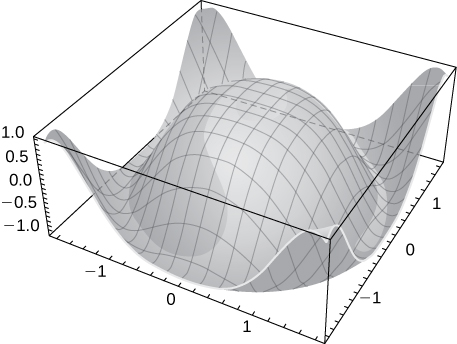
Resposta: $Gráfico de superfície da função z=cos (sqrt (x^2+y^2))$

(46)$ z=y^2−x^2$

47) Descreva as linhas de contorno para vários valores de$ c$$ z=x^2+y^2−2x−2y.$

Resposta: As linhas de contorno são círculos concêntricos centrados no ponto,$ (1, 1) $.
Você pode ver isso completando o quadrado depois de definir essa função igual$c$ a.
Ou seja, escrevemos$ x^2-2x+1+y^2−2y+1 = c + 2 $ o que pode ser reescrito como,$ (x - 1)^2 + (y - 1)^2 = c + 2 $.
Isso nos dá círculos centrados no ponto$ (1, 1) $, cada um com um raio de$ \sqrt{c+2} $.

Nos exercícios, 48 - 52, encontre a superfície nivelada para o valor dado de$c$ para cada função de três variáveis e descreva-a.

48)$ w(x,y,z)=x−2y+z,\quad c=4$

49)$ w(x,y,z)=x^2+y^2+z^2,\quad c=9$

Resposta: $ x^2+y^2+z^2=9$, uma esfera de raio$ 3$

50)$ w(x,y,z)=x^2+y^2−z^2,\quad c=−4$

51)$ w(x,y,z)=x^2+y^2−z^2,\quad c=4$

Resposta: $ x^2+y^2−z^2=4,$um hiperbolóide de uma folha

52)$ w(x,y,z)=9x^2−4y^2+36z^2,\quad c=0$

Nos exercícios 53 a 55, encontre uma equação da curva de nível$ f$ que contém o ponto$ P$.

53)$ f(x,y)=1−4x^2−y^2,\quad P(0,1)$

Resposta: $ 4x^2+y^2=1,$

54)$ g(x,y)=y^2\arctan x,\quad P(1,2)$

55)$ g(x,y)=e^{xy}(x^2+y^2),\quad P(1,0)$

Resposta: $ 1=e^{xy}(x^2+y^2)$

56) A intensidade$ E$ de um campo elétrico no ponto$ (x,y,z)$ resultante de um fio carregado infinitamente longo ao longo do$y$ eixo -é dada por$ E(x,y,z)=k/\sqrt{x^2+y^2}$, onde$ k$ está uma constante positiva. Para simplificar, deixe$ k=1$ e encontre as equações das superfícies niveladas para$ E=10$ e$ E=100.$

57) Uma placa fina feita de ferro está localizada no$xy$ plano A temperatura$ T$ em graus Celsius em um ponto$ P(x,y)$ é inversamente proporcional ao quadrado de sua distância da origem. $ T$Expresse em função de$ x$$ y$ e.

Resposta: $ T(x,y)=\dfrac{k}{x^2+y^2}$

58) Consulte o problema anterior. Usando a função de temperatura encontrada lá, determine a constante de proporcionalidade se a temperatura no ponto$ P(1,2)$ for$ 50°C.$ Use esta constante para determinar a temperatura no ponto$ Q(3,4).$

59) Consulte o problema anterior. Encontre as curvas de nível para$ T=40°C$$ T=100°C,$ e descreva o que as curvas de nível representam.

Resposta: $ x^2+y^2=\dfrac{k}{40}, \quad x^2+y^2=\dfrac{k}{100}$. As curvas de nível representam círculos de raios$ \sqrt{10k}/20$ e$ \sqrt{k}/10$

Colaboradores

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added the contour plots to answers for problems 17, 21 and 29.