13.5: Capítulo 13 Exercícios de revisão
- Page ID
- 187857
Verdadeiro ou falso? Justifique sua resposta com uma prova ou um contra-exemplo.
1. Uma equação paramétrica que passa por pontos\(P\) e\(Q\) pode ser dada por\(\vecs r(t)=⟨t^2,\, 3t+1,\, t−2⟩,\) onde\(P(1,4,−1)\) e\(Q(16,11,2).\)
2. \(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=2\vecs u′(t)×\vecs u(t)\)
- Responda
- Falso,\(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=\vecs 0.\)
3. A curvatura de um círculo de raio\(r\) é constante em todos os lugares. Além disso, a curvatura é igual a\(1/r.\)
4. A velocidade de uma partícula com uma função de posição\(\vecs r(t)\) é\(\dfrac{\vecs r′(t)}{\|\vecs r′(t)\|}.\)
- Responda
- Falso, é\(\|\vecs r′(t)\|\)
Encontre os domínios das funções com valores vetoriais.
5. \(\vecs r(t)=⟨\sin(t),\, \ln(t),\, \sqrt{t}⟩\)
6. \(\vecs r(t)=\left\langle e^t,\,\dfrac{1}{\sqrt{4−t}},\,\sec t\right\rangle\)
- Responda
- \(t<4, \; t≠\dfrac{nπ}{2}\)
Esboce as curvas para as seguintes equações vetoriais. Use uma calculadora, se necessário.
7. [T]\(\vecs r(t)=⟨t^2,\, t^3⟩\)
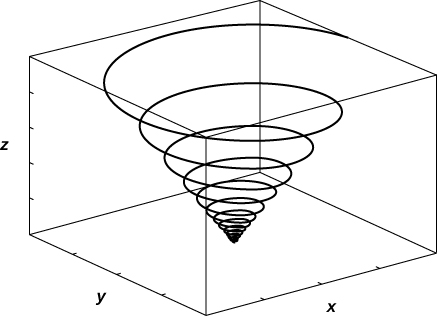
8. [T]\(\vecs r(t)=⟨\sin(20t)e^{−t}, \, \cos(20t)e^{−t}, \, e^{−t}⟩\)
- Responda
Encontre uma função vetorial que descreva as seguintes curvas.
9. Interseção do cilindro\(x^2+y^2=4\) com o plano\(x+z=6\)
10. Interseção do cone\(z=\sqrt{x^2+y^2}\) e do plano\(z=y−4\)
- Responda
- \(\vecs r(t)=\left\langle t, \, 2-\frac{t^2}{8},\, -2 - \frac{t^2}{8}\right\rangle\)
Encontre as derivadas de\(\vecs u(t), \, \vecs u′(t), \, \vecs u′(t)×\vecs u(t), \, \vecs u(t)×\vecs u′(t),\) e\(\vecs u(t)·\vecs u′(t).\) encontre o vetor tangente unitário.
11. \(\vecs u(t)=⟨e^t, \, e^{−t}⟩\)
12. \(\vecs u(t)=⟨t^2,\, 2t+6, \, 4t^5−12⟩\)
- Responda
- \(\vecs u′(t)=⟨2t, \, 2, \, 20t^4⟩,\)
\(\vecs u″(t)=⟨2, \, 0, \, 80t^3⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u′(t)×\vecs u(t)\Big]=⟨−480t^3−160t^4, \, 24+75t^2, \, 12+4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u′(t)\Big]=⟨480t^3+160t^4, \, -24-75t^2, \, -12-4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)⋅\vecs u′(t)\Big]=720t^8−9600t^3+6t^2+4,\)
vetor tangente unitário:\(\vecs T(t)=\dfrac{2t}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat i}+\dfrac{2}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat j}+\dfrac{20t^4}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat k}\)
Avalie os seguintes integrais.
13. \(\displaystyle ∫\left(\tan(t)\sec(t)\,\mathbf{\hat i}−te^{3t}\,\mathbf{\hat j}\right)\, dt\)
14. \(\displaystyle ∫_1^4 \vecs u(t) \, dt,\)com\(\vecs u(t)=\left\langle\dfrac{\ln t}{t}, \, \dfrac{1}{\sqrt{t}}, \, \sin\left(\frac{tπ}{4}\right)\right\rangle\)
- Responda
- \(\dfrac{\ln(4^2)}{2}\,\mathbf{\hat i}+2\,\mathbf{\hat j}+\dfrac{2(2+\sqrt{2})}{\pi}\,\mathbf{\hat k}\)
Encontre o comprimento das curvas a seguir.
15. \(\vecs r(t)=⟨3t,\, 4\cos t, \, 4\sin t ⟩\)para\(1≤t≤4\)
16. \(\vecs r(t)=2\,\mathbf{\hat i}+t\,\mathbf{\hat j}+3t^2\,\mathbf{\hat k}\)para\(0≤t≤1\)
- Responda
- \(\dfrac{\sqrt{37}}{2}+\frac{1}{12}\sinh^{−1} 6\)
Reparametrize as seguintes funções com relação ao comprimento do arco medido\(t=0\) na direção do aumento\(t.\)
17. \(\vecs r(t)=2t\,\mathbf{\hat i}+(4t−5)\,\mathbf{\hat j}+(1−3t)\,\mathbf{\hat k}\)
18. \(\vecs r(t)=\cos(2t)\,\mathbf{\hat i}+8t\,\mathbf{\hat j}−\sin(2t)\,\mathbf{\hat k}\)
- Responda
- \(\vecs r(t(s))=\cos\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat i}+\frac{8s}{\sqrt{65}}\,\mathbf{\hat j}−\sin\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat k}\)
Encontre a curvatura para as seguintes funções vetoriais.
19. \(\vecs r(t)=(2\sin t)\,\mathbf{\hat i}−4t\,\mathbf{\hat j}+(2\cos t)\,\mathbf{\hat k}\)
20. \(\vecs r(t)=\sqrt{2}e^t\,\mathbf{\hat i}+\sqrt{2}e^{−t}\,\mathbf{\hat j}+2t\,\mathbf{\hat k}\)
- Responda
- \(\dfrac{e^{2t}}{\left(e^{2t}+1\right)^2}\)
21. Encontre o vetor tangente unitário, o vetor normal unitário e o vetor binormal para\(\vecs r(t)=2\cos t\,\mathbf{\hat i} +3t\,\mathbf{\hat j}+2sint\,\mathbf{\hat k}.\)
22. Encontre os componentes de aceleração tangencial e normal com o vetor de posição\(\vecs r(t)=⟨\cos t,\, \sin t, \, e^t⟩.\)
- Responda
- \(a_T=\dfrac{e^{2t}}{1+e^{2t}},\)
\(a_N=\dfrac{\sqrt{2e^{2t}+4e^{2t}\sin t\cos t+1}}{1+e^{2t}}\)
23. Um carro de roda gigante está se movendo a uma velocidade constante\(v\) e tem um raio constante.\(r.\) Encontre a aceleração tangencial e normal do carro de roda gigante.
24. A posição de uma partícula é dada por\(\vecs r(t)=⟨t^2, \, \ln t, \, \sin(πt)⟩,\) onde\(t\) é medida em segundos e\(r\) é medida em metros. Encontre as funções de velocidade, aceleração e velocidade. Qual é a posição, velocidade, velocidade e aceleração da partícula em 1 segundo?
- Responda
- \(\vecs v(t)=\left\langle 2t,\, \frac{1}{t}, \, \pi\cos(πt)\right\rangle\text{ m/sec},\)
\(\vecs a(t)=\left\langle 2, \, −\frac{1}{t^2}, \, −\pi^2\sin(πt) \right\rangle\text{ m/sec}^2,\)
\(\text{speed}(t)=\sqrt{4t^2+\frac{1}{t^2}+\pi^2\cos^2(πt)}\text{ m/sec}\);
Em\(t=1,\; \vecs r(1)=⟨1,0,0⟩\) m,\(\vecs v(1)=⟨2,−1,\pi⟩\) m/seg,\(\vecs a(1)=⟨2,−1,0⟩\) m/sec 2 e\(\text{speed}(1) =\sqrt{5+\pi^2}\) m/seg
Os problemas a seguir consideram o lançamento de uma bala de canhão a partir de um canhão. A bala de canhão é disparada para fora do canhão com um ângulo\(θ\) e velocidade inicial.\(\vecs v_0.\) A única força que atua sobre a bala de canhão é a gravidade, então começamos com uma aceleração constante\(\vecs a(t)=−g\,\mathbf{\hat j}.\)
25. Encontre a função vetorial de velocidade\(\vecs v(t).\)
26. Encontre o vetor de posição\(\vecs r(t)\) e a representação paramétrica da posição.
- Responda
- \(\vecs r(t)=\vecs v_0t−\dfrac{gt^2}{2}\,\mathbf{\hat j},\)
\(\vecs r(t)=⟨v_0(\cos θ)t,\,v_0(\sin θ)t,−\dfrac{gt^2}{2}⟩\)onde\(v_0 = \|\vecs v_0\|.\)
27. Em que ângulo você precisa disparar a bala de canhão para que a distância horizontal seja maior? Qual é a distância total que ele percorreria?


