Skip to main content
Global

12.8: Capítulo 12 Exercícios de revisão

  1. Last updated
  2. Save as PDF
  • Page ID
    187790

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Para os exercícios 1 a 4, determine se a afirmação é verdadeira ou falsa. Justifique a resposta com uma prova ou um contra-exemplo.

    1) Para vetores\(\vecs a\)\(\vecs b\) e qualquer escalar dado\( c, \, c(\vecs a⋅\vecs b)=(c\vecs a)⋅\vecs b.\)

    Responda
    Verdadeiro; veja a prova na Seção 11.3

    2) Para vetores\(\vecs a\)\(\vecs b\) e qualquer escalar dado\( c, \, c(\vecs a×\vecs b)=(c\vecs a)×\vecs b\).

    3) A equação simétrica para a linha de interseção entre dois planos\( x+y+z=2\) e\( x+2y−4z=5\) é dada por\( −\frac{x−1}{6}=\frac{y−1}{5}=z.\)

    Responda
    Falso, convertendo as equações simétricas acima para as equações paramétricas da reta, obtemos:
    \(x = 1 - 6t\)
    \(y = 1 + 5t\)
    \(z = t\)

    Se essa linha estiver em cada plano, devemos obter uma identidade (como 5 = 5) quando substitua cada expressão de\(t\) na equação de cada plano.

    Substituindo na equação do primeiro plano, obtemos:\( (1-6t) + (1+5t) + t = 2\,\checkmark\)

    Assim, sabemos que essa linha está no primeiro plano.

    Mas quando substituímos a equação do segundo plano, obtemos:\( (1 - 6t) + 2(1 + 5t) - 4(t) = 1 - 6t + 2 + 10t - 4t = 3 \neq 5\)

    Como não obtemos uma identidade, sabemos que essa linha não está no segundo plano e, portanto, não pode ser a linha de interseção do dois aviões.

    4) Se\(\vecs a⋅\vecs b=0,\) então\(\vecs a\) for perpendicular\(\vecs b\) a.

    Responda
    Falso, já que\(\vecs a\) ou também\(\vecs b\) pode ser o vetor zero.

    Para os exercícios 5 e 6, use os vetores fornecidos para encontrar as quantidades.

    5)\(\vecs a=9\hat{\mathbf{i}}−2\hat{\mathbf{j}},\quad \vecs b=−3\hat{\mathbf{i}}+\hat{\mathbf{k}}\)

    uma.\( 3\vecs a+\vecs b\)

    b.\( \|\vecs a\|\)

    c.\(\vecs a×\|\vecs b×\vecs a\|\)

    d.\( \|\vecs b×\vecs a\|\)

    Responda
    a.\( ⟨24,−6, 1⟩\)
    b.\( \sqrt{85}\)
    c. Não é possível cruzar um vetor com um escalar
    d.\( 11\)

    6)\(\vecs a=2\hat{\mathbf{i}}+\hat{\mathbf{j}}−9\hat{\mathbf{k}},\quad \vecs b=−\hat{\mathbf{i}}+2\hat{\mathbf{k}},\quad \vecs c=4\hat{\mathbf{i}}−2\hat{\mathbf{j}}+\hat{\mathbf{k}}\)

    uma.\( 2\vecs a−\vecs b\)

    b.\( \|\vecs b×\vecs c\|\)

    c.\( \vecs b×\left(\vecs b×\vecs c\right)\)

    d.\( \vecs c×\|\vecs b×\vecs a\|\)

    e.\( \text{Proj}_\vecs{a}\vecs b\)

    7) Encontre os valores de\(a\) tal que os\( ⟨2,4,a⟩\) vetores\( ⟨0,−1,a⟩\) sejam ortogonais.

    Responda
    \( a=±2\)

    Para os exercícios 8 e 9, encontre os vetores unitários.

    8) Encontre o vetor unitário que tem a mesma direção do vetor\(\vecs v\) que começa\( (0,−3)\) e termina em\( (4,10).\)

    9) Encontre o vetor unitário que tem a mesma direção do vetor\(\vecs v\) que começa\( (1,4,10)\) e termina em\( (3,0,4).\)

    Responda
    \( ⟨\frac{1}{\sqrt{14}},−\frac{2}{\sqrt{14}},−\frac{3}{\sqrt{14}}⟩ = ⟨\frac{\sqrt{14}}{14},−\frac{\sqrt{14}}{7},−\frac{3\sqrt{14}}{14}⟩ \)

    Para os exercícios 10 e 11, encontre a área ou o volume das formas dadas.

    10) O paralelogramo abrangido por vetores\(\vecs a=⟨1,13⟩\) e\(\vecs b=⟨3,21⟩\)

    11) O paralelepípedo formado por\(\vecs a=⟨1,4,1⟩\) e\(\vecs b=⟨3,6,2⟩,\) e\(\vecs c=⟨−2,1,−5⟩\)

    Responda
    \( 27\)unidades\(^2\)

    Para os exercícios 12 e 13, encontre as equações paramétricas e a equação vetorial da linha com as propriedades dadas.

    12) A linha que passa pelo ponto\( (2,−3,7)\) que é paralelo ao vetor\( ⟨1,3,−2⟩\)

    13) A linha que passa por pontos\( (1,3,5)\) e\( (−2,6,−3)\)

    Responda
    \( x=1−3t,y=3+3t,z=5−8t,\quad \vecs r(t)=(1−3t)\hat{\mathbf{i}}+3(1+t)\hat{\mathbf{j}}+(5−8t)\hat{\mathbf{k}}\)

    Para os exercícios 14 e 15, encontre a equação do plano com as propriedades dadas.

    14) O plano que passa pelo ponto\( (4,7,−1)\) e tem vetor normal\(\vecs n=⟨3,4,2⟩\)

    15) O avião que passa por pontos\( (0,1,5),(2,−1,6),\) e\( (3,2,5).\)

    Responda
    \( −x+3y+8z=43\)

    Para os exercícios 16 e 17, encontre os traços das superfícies em planos e\( x=k,y=k\), em\( z=k.\) seguida, descreva e desenhe as superfícies.

    16)\( 9x^2+4y^2−16y+36z^2=20\)

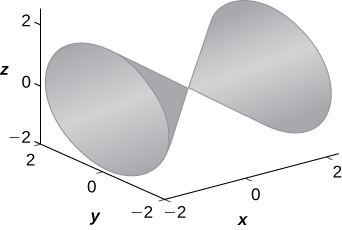
    17)\( x^2=y^2+z^2\)

    Responda
    \( x=k\)trace:\( k^2=y^2+z^2\) é um círculo,\( y=k\) trace:\( x^2−z^2=k^2\) é uma hipérbole (ou um par de linhas se\( k=0), z=k\) traço:\( x^2−y^2=k^2\) é uma hipérbole (ou um par de linhas se\( k=0\)). A superfície é um cone.

    Para os exercícios 18 e 19, escreva a equação dada em coordenadas cilíndricas e coordenadas esféricas.

    18)\( x^2+y^2+z^2=144\)

    19)\( z=x^2+y^2−1\)

    Responda
    Cilíndrico:\( z=r^2−1,\) esférico:\( \cos φ=ρ\sin^2 φ−\frac{1}{ρ}\)

    Para os exercícios 20 e 21, converta as equações dadas de coordenadas cilíndricas ou esféricas em coordenadas retangulares. Identifique a superfície dada.

    20)\( ρ^2(\sin^2(φ)−\cos^2(φ))=1\)

    21)\( r^2−2r\cos(θ)+z^2=1\)

    Responda
    \( x^2−2x+y^2+z^2=1\), esfera

    Para os exercícios 22 e 23, considere um pequeno barco atravessando um rio.

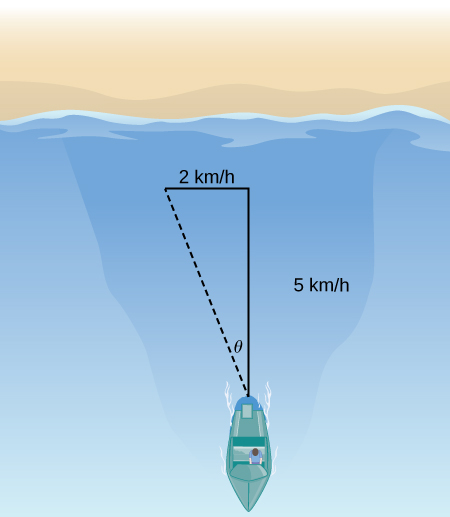
    22) Se a velocidade do barco for\( 5\) km/h para o norte em água parada e a água tiver uma corrente de\( 2\) km/h para oeste (veja a figura a seguir), qual é a velocidade do barco em relação à costa? Qual é o ângulo em\( θ\) que o barco está realmente viajando?

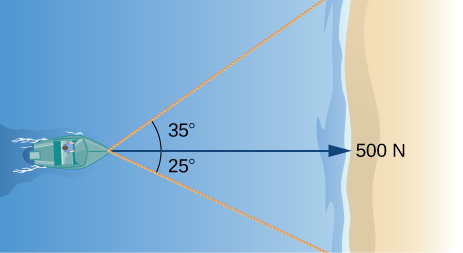
    23) Quando o barco chega à costa, duas cordas são lançadas às pessoas para ajudar a puxar o barco para a costa. Uma corda está em um ângulo de\( 25°\) e a outra está em\( 35°\). Se o barco precisar ser puxado em linha reta e com uma força de\( 500\) N, determine a magnitude da força para cada corda (veja a figura a seguir).

    Responda
    331 N e 244 N

    24) Um avião está voando na direção de 52° leste do norte com uma velocidade de 450 mph. Um vento forte tem um rumo de 33° a leste do norte com uma velocidade de 50 mph. Qual é a velocidade de solo e o rumo resultantes do avião?

    25) Calcule o trabalho realizado movendo uma partícula da posição\( (1,2,0)\) para a ao\( (8,4,5)\) longo de uma linha reta com uma força\(\vecs F=2\hat{\mathbf{i}}+3\hat{\mathbf{j}}−\hat{\mathbf{k}}.\)

    Responda
    \( 15\)J

    Nos problemas 26 e 27, considere sua tentativa malsucedida de tirar o pneu do carro usando uma chave inglesa para soltar os parafusos. Suponha que a chave tenha\( 0.3\) m de comprimento e você possa aplicar uma força de 200 N.

    26) Como seu pneu está furado, você só pode aplicar sua força em um\( 60°\) ângulo. Qual é o torque no centro do parafuso? Suponha que essa força não seja suficiente para soltar o parafuso.

    27) Alguém lhe empresta um macaco de pneu e agora você pode aplicar uma força de 200-N em um\( 80°\) ângulo. O torque resultante será maior ou menor? Qual é o novo torque resultante no centro do parafuso? Suponha que essa força não seja suficiente para soltar o parafuso.

    Responda
    Mais,\( 59.09\) J