Skip to main content
Global

12.7E: Exercícios para a Seção 12.7

  1. Last updated
  2. Save as PDF
  • Page ID
    187778

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Use a figura a seguir como auxílio na identificação da relação entre os sistemas de coordenadas retangulares, cilíndricas e esféricas.

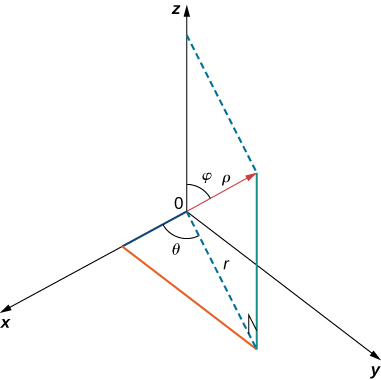
    Para os exercícios 1 a 4, as coordenadas cilíndricas\( (r,θ,z)\) de um ponto são fornecidas. Encontre as coordenadas retangulares\( (x,y,z)\) do ponto.

    1)\( \left(4,\frac{π}{6},3\right)\)

    Resposta
    \( (2\sqrt{3},2,3)\)

    2)\( \left(3,\frac{π}{3},5\right)\)

    3)\( \left(4,\frac{7π}{6},3\right)\)

    Resposta
    \( (−2\sqrt{3},−2,3)\)

    4)\( (2,π,−4)\)

    Para os exercícios 5 a 8, as coordenadas retangulares\( (x,y,z)\) de um ponto são fornecidas. Encontre as coordenadas cilíndricas\( (r,θ,z)\) do ponto.

    5)\( (1,\sqrt{3},2)\)

    Resposta
    \( \left(2,\frac{π}{3},2\right)\)

    6)\( (1,1,5)\)

    7)\( (3,−3,7)\)

    Resposta
    \( \left(3\sqrt{2},−\frac{π}{4},7\right)\)

    8)\( (−2\sqrt{2},2\sqrt{2},4)\)

    Para os exercícios 9 a 16, a equação de uma superfície em coordenadas cilíndricas é dada. Encontre a equação da superfície em coordenadas retangulares. Identifique e faça um gráfico da superfície.

    9) [T]\( r=4\)

    Resposta

    Um cilindro de equação\( x^2+y^2=16,\) com seu centro na origem e regras paralelas ao\(z\) eixo -,

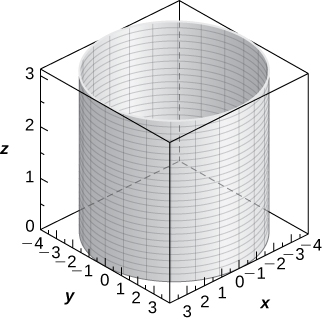
    10) [T]\( z=r^2\cos^2θ\)

    11) [T]\( r^2\cos(2θ)+z^2+1=0\)

    Resposta

    Hiperbolóide de duas folhas de equação\( −x^2+y^2−z^2=1,\) com o\(y\) eixo -como eixo de simetria,

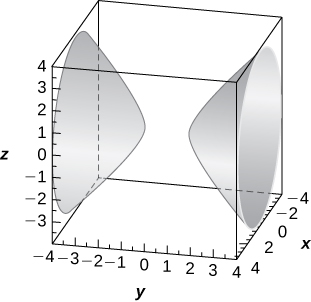
    12) [T]\( r=3\sin θ\)

    13) [T]\( r=2\cos θ\)

    Resposta

    Cilindro de equação\( x^2−2x+y^2=0,\) com centro em\( (1,0,0)\) e raio\( 1\), com decisões paralelas ao\(z\) eixo -,

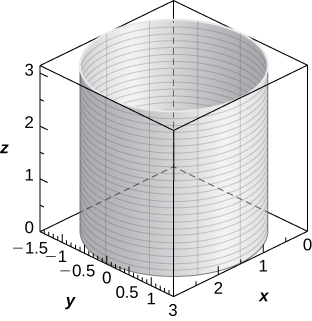
    14) [T]\( r^2+z^2=5\)

    15) [T]\( r=2\sec θ\)

    Resposta

    Plano da equação\( x=2,\)

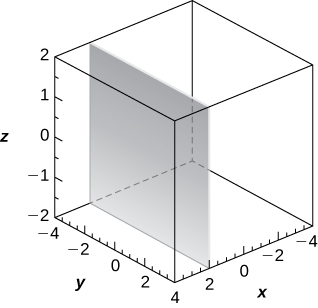
    16) [T]\( r=3\csc θ\)

    Para os exercícios 17 a 22, a equação de uma superfície em coordenadas retangulares é dada. Encontre a equação da superfície em coordenadas cilíndricas.

    17)\( z=3\)

    Resposta
    \( z=3\)

    18)\( x=6\)

    19)\( x^2+y^2+z^2=9\)

    Resposta
    \( r^2+z^2=9\)

    20)\( y=2x^2\)

    21)\( x^2+y^2−16x=0\)

    Resposta
    \( r=16\cos θ,\quad r=0\)

    22)\( x^2+y^2−3\sqrt{x^2+y^2}+2=0\)

    Para os exercícios 23 a 26, as coordenadas esféricas\( (ρ,θ,φ)\) de um ponto são fornecidas. Encontre as coordenadas retangulares\( (x,y,z)\) do ponto.

    23)\( (3,0,π)\)

    Resposta
    \( (0,0,−3)\)

    24)\( \left(1,\frac{π}{6},\frac{π}{6}\right)\)

    25)\( \left(12,−\frac{π}{4},\frac{π}{4}\right)\)

    Resposta
    \( (6,−6,\sqrt{2})\)

    26)\( \left(3,\frac{π}{4},\frac{π}{6}\right)\)

    Para os exercícios 27 a 30, as coordenadas retangulares\( (x,y,z)\) de um ponto são fornecidas. Encontre as coordenadas esféricas\( (ρ,θ,φ)\) do ponto. Expresse a medida dos ângulos em graus arredondados para o número inteiro mais próximo.

    27)\( (4,0,0)\)

    Resposta
    \( (4,0,90°)\)

    28)\( (−1,2,1)\)

    29)\( (0,3,0)\)

    Resposta
    \( (3,90°,90°)\)

    30)\( (−2,2\sqrt{3},4)\)

    Para os exercícios 31 a 36, a equação de uma superfície em coordenadas esféricas é dada. Encontre a equação da superfície em coordenadas retangulares. Identifique e faça um gráfico da superfície.

    31) [T]\( ρ=3\)

    Resposta

    Esfera da equação\( x^2+y^2+z^2=9\) centrada na origem com raio\( 3\),

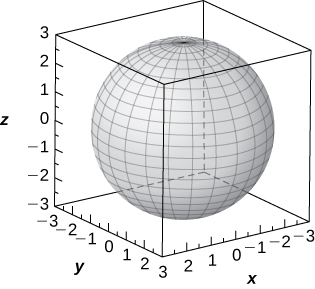
    32) [T]\( φ=\frac{π}{3}\)

    33) [T]\( ρ=2\cos φ\)

    Resposta

    Esfera da equação\( x^2+y^2+(z−1)^2=1\) centrada em\( (0,0,1)\) com raio\( 1\),

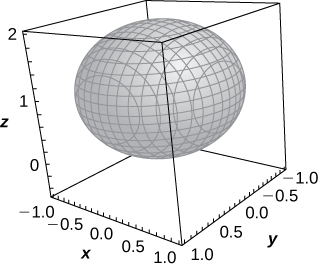
    34) [T]\( ρ=4\csc φ\)

    35) [T]\( φ=\frac{π}{2}\)

    Resposta

    O\(xy\) plano -da equação\( z=0,\)

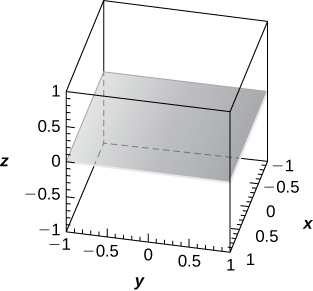
    36) [T]\( ρ=6\csc φ\sec θ\)

    Para os exercícios 37 a 40, a equação de uma superfície em coordenadas retangulares é dada. Encontre a equação da superfície em coordenadas esféricas. Identifique a superfície.

    37)\( x^2+y^2−3z^2=0, \quad z≠0\)

    Resposta
    \( φ=\frac{π}{3}\)ou cone\( φ=\frac{2π}{3};\) elíptico

    38)\( x^2+y^2+z^2−4z=0\)

    39)\( z=6\)

    Resposta
    \( ρ\cos φ=6;\)Avião em\( z=6\)

    40)\( x^2+y^2=9\)

    Para os exercícios 41 a 44, as coordenadas cilíndricas de um ponto são fornecidas. Encontre suas coordenadas esféricas associadas, com a medida do ângulo φ em radianos arredondada para quatro casas decimais.

    41) [T]\( \left(1,\frac{π}{4},3\right)\)

    Resposta
    \( \left(\sqrt{10},\frac{π}{4},0.3218\right)\)

    42) [T]\( (5,π,12)\)

    43)\( \left(3,\frac{π}{2},3\right)\)

    Resposta
    \( (3\sqrt{2},\frac{π}{2},\frac{π}{4})\)

    44)\( \left(3,−\frac{π}{6},3\right)\)

    Para os exercícios 45 a 48, as coordenadas esféricas de um ponto são fornecidas. Encontre suas coordenadas cilíndricas associadas.

    45)\( \left(2,−\frac{π}{4},\frac{π}{2}\right)\)

    Resposta
    \( \left(2,−\frac{π}{4},0\right)\)

    (46)\( \left(4,\frac{π}{4},\frac{π}{6}\right)\)

    47)\( \left(8,\frac{π}{3},\frac{π}{2}\right)\)

    Resposta
    \( \left(8,\frac{π}{3},0\right)\)

    48)\( \left(9,−\frac{π}{6},\frac{π}{3}\right)\)

    Para os exercícios 49 a 52, encontre o sistema de coordenadas mais adequado para descrever os sólidos.

    49) O sólido situado no primeiro octante com um vértice na origem e cercado por um cubo de comprimento de aresta\( a\), onde\( a>0\)

    Resposta
    Sistema cartesiano,\( \big\{(x,y,z)\,|\,0≤x≤a,\;0≤y≤a,\;0≤z≤a\big\}\)

    50) Uma concha esférica determinada pela região entre duas esferas concêntricas centradas na origem, de raios de\( a\) e\( b\), respectivamente, onde\( b>a>0\)

    51) Uma esfera interna sólida\( x^2+y^2+z^2=9\) e um cilindro externo\( \left(x−\frac{3}{2}\right)^2+y^2=\frac{9}{4}\)

    Resposta
    Sistema cilíndrico,\( \big\{(r,θ,z)\,|\,r^2+z^2≤9,\;r≥3\cos θ,\;0≤θ≤2π\big\}\)

    52) Uma concha cilíndrica de altura\( 10\) determinada pela região entre dois cilindros com o mesmo centro, réguas paralelas e raios de\( 2\) e\( 5\), respectivamente

    53) [T] Use um CAS ou Calcplot3d para representar graficamente em coordenadas cilíndricas a região entre o parabolóide elíptico\( z=x^2+y^2\) e o cone\( x^2+y^2−z^2=0.\)

    Resposta

    A região é descrita pelo conjunto de pontos\( \big\{(r,θ,z)\,|\,0≤r≤1,\;0≤θ≤2π,\;r^2≤z≤r\big\}.\)

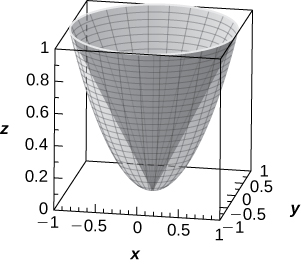
    54) [T] Use um CAS ou Calcplot3d para representar graficamente em coordenadas esféricas a “região do cone de sorvete” situada acima do plano xy entre a esfera\( x^2+y^2+z^2=4\) e o cone elíptico\( x^2+y^2−z^2=0.\)

    55) Washington, DC, está localizada em\( 39°\) N e\( 77°\) W (veja a figura a seguir). Suponha que o raio da Terra seja\( 4000\) mi. Expresse a localização de Washington, DC, em coordenadas esféricas.

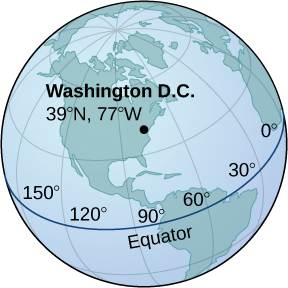
    Resposta
    \( (4000,−77°,51°)\)

    56) São Francisco está localizado em\( 37.78°N\) e\( 122.42°W.\) suponha que o raio da Terra seja\( 4000\) mi. Expresse a localização de São Francisco em coordenadas esféricas.

    57) Encontre a latitude e longitude do Rio de Janeiro se suas coordenadas esféricas forem\( (4000,−43.17°,102.91°).\)

    Resposta
    \( 43.17°W, 22.91°S\)

    58) Encontre a latitude e longitude de Berlim se suas coordenadas esféricas forem\( (4000,13.38°,37.48°).\)

    59) [T] Considere o toro da equação\( \big(x^2+y^2+z^2+R^2−r^2\big)^2=4R^2(x^2+y^2),\) onde\( R≥r>0.\)

    a. Escreva a equação do toróide em coordenadas esféricas.

    b. Se\( R=r,\) a superfície for chamada de toróide de chifre. Mostre que a equação de um toróide de chifre em coordenadas esféricas é\( ρ=2R\sin φ.\)

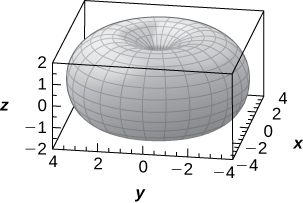
    c. Use um CAS ou CalcPlot3d para representar graficamente o toróide da buzina\( R=r=2\) em coordenadas esféricas.

    Resposta

    uma.\(ρ=0, \quad ρ+R^2−r^2−2R\sin φ=0\)

    c.

    60) [T] A “esfera irregular” com uma equação em coordenadas esféricas é\( ρ=a+b\cos(mθ)\sin(nφ)\), com\( θ∈[0,2π]\) e\( φ∈[0,π]\), onde e são números positivos\( a\) e\( b\) são números inteiros positivos, pode ser usada em matemática aplicada para modelar o crescimento tumoral.\( m\)\( n\)

    a. Mostre que a “esfera irregular” está contida dentro de uma esfera de equação\( ρ=a+b.\) Encontre os valores\( θ\) e\( φ\) nos quais as duas superfícies se cruzam.

    b. Use um CAS ou CalcPlot3d para representar graficamente a superfície para\( a=14, b=2, m=4,\) e\( n=6\) junto com a esfera\( ρ=a+b.\)

    c. Encontre a equação da curva de interseção da superfície em b. com o cone\( φ=\frac{π}{12}\). Faça um gráfico da curva de interseção no plano de interseção.

    Colaboradores

    Template:ContribOpenStaxCalc

    Links para Calcplot3d adicionados por Paul Seeburger (Monroe Community College).