12.2: Vetores em três dimensões

Last updated
Save as PDF

Page ID: 187763

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Descreva o espaço tridimensional matematicamente.
Localize pontos no espaço usando coordenadas.
Escreva a fórmula da distância em três dimensões.
Escreva as equações para planos e esferas simples.
Execute operações vetoriais em$\mathbb{R}^{3}$.

Os vetores são ferramentas úteis para resolver problemas bidimensionais. A vida, no entanto, acontece em três dimensões. Para expandir o uso de vetores para aplicações mais realistas, é necessário criar uma estrutura para descrever o espaço tridimensional. Por exemplo, embora um mapa bidimensional seja uma ferramenta útil para navegar de um lugar para outro, em alguns casos a topografia da terra é importante. Sua rota planejada passa pelas montanhas? Você tem que atravessar um rio? Para apreciar totalmente o impacto dessas características geográficas, você deve usar três dimensões. Esta seção apresenta uma extensão natural do plano coordenado cartesiano bidimensional em três dimensões.

Sistemas de coordenadas tridimensionais

Como aprendemos, o sistema de coordenadas retangulares bidimensional contém dois eixos perpendiculares: o$x$ eixo horizontal e o $y$eixo vertical. Podemos adicionar uma terceira dimensão, o$z$ eixo -, que é perpendicular ao$x$ eixo -e ao$y$ eixo -. Chamamos esse sistema de sistema de coordenadas retangulares tridimensionais. Ela representa as três dimensões que encontramos na vida real.

Definição: Sistema de coordenadas retangulares tridimensional

O sistema de coordenadas retangulares tridimensional consiste em três eixos perpendiculares: o$x$ eixo$y$ -, o eixo -e o$z$ eixo -. Como cada eixo é uma linha numérica representando todos os números reais em$ℝ$, o sistema tridimensional geralmente é indicado por$ℝ^3$.

Na Figura$\PageIndex{1a}$, o $z$eixo -positivo é mostrado acima do plano que contém os$y$ eixos$x$ - e -. O$x$ eixo -positivo aparece à esquerda e o$y$ eixo -positivo está à direita. Uma pergunta natural a ser feita é: Como esse arranjo foi determinado? O sistema exibido segue a regra da mão direita. Se pegarmos nossa mão direita e alinharmos os dedos com o$x$ eixo positivo, então enrole os dedos para que eles apontem na direção do $y$eixo positivo, nosso polegar aponta na direção do$z$ eixo positivo (Figura$\PageIndex{1b}$). Neste texto, sempre trabalhamos com sistemas de coordenadas configurados de acordo com a regra da mão direita. Alguns sistemas seguem uma regra da mão esquerda, mas a regra da mão direita é considerada a representação padrão.

Esta figura tem duas imagens. O primeiro é um sistema de coordenadas tridimensional. O eixo x está para frente, o eixo y é horizontal para a esquerda e para a direita e o eixo z é vertical. A segunda imagem são os eixos tridimensionais do sistema de coordenadas com a mão direita. O polegar está apontando para o eixo z positivo, com os dedos enrolando o eixo z do eixo x positivo para o eixo y positivo. — Figura$\PageIndex{1}$: (a) Podemos estender o sistema de coordenadas retangulares bidimensional adicionando um terceiro eixo, o$z$ eixo -, que é perpendicular ao$x$ eixo -e ao$y$ eixo -. (b) A regra da mão direita é usada para determinar o posicionamento dos eixos de coordenadas no plano cartesiano padrão.

Em duas dimensões, descrevemos um ponto no plano com as coordenadas$(x,y)$. Cada coordenada descreve como o ponto se alinha com o eixo correspondente. Em três dimensões, uma nova coordenada,$z$, é anexada para indicar o alinhamento com o$z$ eixo -:$(x,y,z)$. Um ponto no espaço é identificado pelas três coordenadas (Figura$\PageIndex{2}$). Para traçar o ponto$(x,y,z)$, coloque$x$ as unidades ao longo do $x$eixo -, depois $y$as unidades na direção do$y$ eixo -e, em seguida, as$z$ unidades na direção do$z$ eixo.

Essa figura é a octante positiva do sistema de coordenadas tridimensional. No primeiro octante, há um sólido retangular desenhado com linhas quebradas. Um canto é rotulado (x, y, z). A altura da caixa é rotulada como “unidades z”, a largura é rotulada como “x unidades” e o comprimento é rotulado como “unidades y”. — Figura$\PageIndex{2}$: Para traçar o ponto$(x,y,z)$,$x$ coloque unidades ao longo do$x$ eixo -, depois$y$ unidades na direção do$y$ eixo -e, em seguida,$z$ unidades na direção do$z$ eixo -.

Exemplo$\PageIndex{1}$: Locating Points in Space

Esboce o ponto$(1,−2,3)$ no espaço tridimensional.

Solução

Para esboçar um ponto, comece desenhando três lados de um prisma retangular ao longo dos eixos coordenados: uma unidade na$x$ direção positiva,$2$ unidades na$y$ direção negativa e$3$ unidades na$z$ direção positiva. Complete o prisma para traçar o ponto (Figura$\PageIndex{3}$).

Esta figura é o sistema de coordenadas tridimensional. No quarto octante há um sólido retangular desenhado. Um canto é rotulado (1, -2, 3). — Figura$\PageIndex{3}$: Esboçando o ponto$(1,−2,3).$

Exercício$\PageIndex{1}$

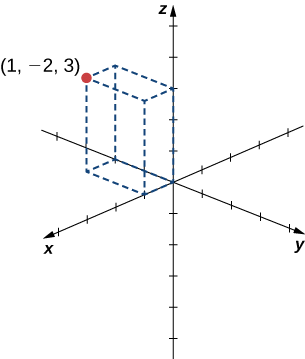
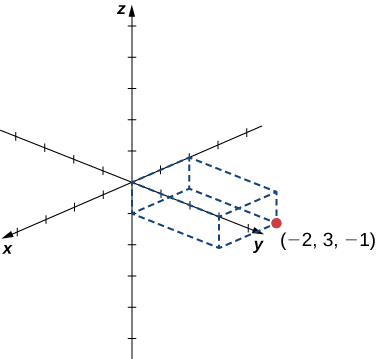
Esboce o ponto$(−2,3,−1)$ no espaço tridimensional.

Dica: Comece desenhando os eixos coordenados. por exemplo, Figura$\PageIndex{3}$. Em seguida, desenhe um prisma retangular para ajudar a encontrar o ponto no espaço.
Responda: $Esta figura é o sistema de coordenadas tridimensional. No primeiro octante, há um sólido retangular desenhado. Um canto é rotulado (-2, 3, -1).$

No espaço bidimensional, o plano coordenado é definido por um par de eixos perpendiculares. Esses eixos nos permitem nomear qualquer local dentro do avião. Em três dimensões, definimos planos de coordenadas pelos eixos coordenados, assim como em duas dimensões. Existem três eixos agora, então há três pares de eixos que se cruzam. Cada par de eixos forma um plano coordenado: o$xy$ plano -, o $xz$plano -e o$yz$ plano -( Figura$\PageIndex{4}$). Definimos o$xy$ plano -formalmente como o seguinte conjunto:$\{(x,y,0):x,y∈ℝ\}.$ Da mesma forma, o $xz$-plane e o$yz$ -plane são definidos como$\{(x,0,z):x,z∈ℝ\}$ e$\{(0,y,z):y,z∈ℝ\},$ respectivamente.

Para visualizar isso, imagine que você está construindo uma casa e está em uma sala com apenas duas das quatro paredes acabadas. (Suponha que as duas paredes acabadas sejam adjacentes uma à outra.) Se você ficar de costas para o canto onde as duas paredes acabadas se encontram, voltadas para a sala, o chão é o$xy$ plano -, a parede à sua direita é o $xz$plano -e a parede à sua esquerda é o $yz$plano -.

Essa figura é a primeira octante de um sistema de coordenadas tridimensional. Além disso, há o plano x y representado por um retângulo com os eixos x e y no plano. Há também o plano x z nos eixos x e z e o plano y z nos eixos y e z. — Figura$\PageIndex{4}$: O plano contendo os eixos$x$ *$y$- e -* é chamado de$xy$ plano -. O plano contendo os$z$ eixos$x$ - e -é chamado de$xz$ plano -, e os$z$ eixos$y$ - e -definem o$yz$ plano -.

Em duas dimensões, os eixos de coordenadas dividem o plano em quatro quadrantes. Da mesma forma, os planos coordenados dividem o espaço entre eles em oito regiões sobre a origem, chamadas octantes. Os octantes são$ℝ^3$ preenchidos da mesma forma que os quadrantes$ℝ^2$, conforme mostrado na Figura$\PageIndex{5}$.

Esta figura é o sistema de coordenadas tridimensional com o primeiro octante marcado com um número romano I, I, II, III, IV, V, VI, VII e VIII. Além disso, para cada quadrante existem os sinais dos valores de x, y e z. Eles são: I (+, +, +); 2º (-, +, +); 3º (-, -, +); 4º (+, -, +); 5º (+, +, -); 6º (-, +, -); 7º (-, -, -); e 8º (+, -, -) -, -). — Figura$\PageIndex{5}$: Os pontos que estão em octantes têm três coordenadas diferentes de zero.

A maioria dos trabalhos no espaço tridimensional é uma extensão confortável dos conceitos correspondentes em duas dimensões. Nesta seção, usamos nosso conhecimento de círculos para descrever esferas e, em seguida, expandimos nossa compreensão dos vetores para três dimensões. Para atingir esses objetivos, começamos adaptando a fórmula da distância ao espaço tridimensional.

Se dois pontos estiverem no mesmo plano de coordenadas, é fácil calcular a distância entre eles. Sabemos que a distância$d$ entre dois pontos$(x_1,y_1)$ e$(x_2,y_2)$ no plano da$xy$ coordenada -é dada pela fórmula

\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]

A fórmula para a distância entre dois pontos no espaço é uma extensão natural dessa fórmula.

A distância entre dois pontos no espaço

A distância$d$ entre os pontos$(x_1,y_1,z_1)$ e$(x_2,y_2,z_2)$ é dada pela fórmula

\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}. \label{distanceForm} \]

A prova desse teorema é deixada como um exercício. (Dica: primeiro encontre a distância$d_1$ entre os pontos$(x_1,y_1,z_1)$ e$(x_2,y_2,z_1)$ conforme mostrado na Figura$\PageIndex{6}$.)

Esta figura é um prisma retangular. O canto inferior esquerdo traseiro é rotulado como “P sub 1= (x sub 1, y sub 1, z sub 1). O canto inferior frontal direito é rotulado como “(x sub 2, y sub 2, z sub 1)”. Há uma linha entre P sub 1 e P sub 2 e é rotulada como “d sub 1”. O canto superior direito frontal é rotulado como “P sub 2= (x sub 2, y sub 2, z sub 2)”. Há uma linha de P sub 1 a P sub 2 e é rotulada como “d (P sub 1, P sub 2)”. O lado vertical frontal direito é rotulado como “|z sub 2-z sub 1|”. — Figura$\PageIndex{6}$: A distância entre$P_1$ e$P_2$ é o comprimento da diagonal do prisma retangular com$P_1$ e$P_2$ como cantos opostos.

Exemplo$\PageIndex{2}$: Distance in Space

Encontre a distância entre os pontos$P_1=(3,−1,5)$ e$P_2=(2,1,−1).$

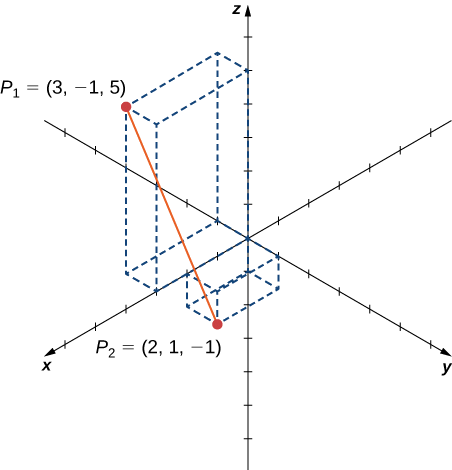
Esta figura é o sistema de coordenadas tridimensional. Há dois pontos. O primeiro é rotulado como “P sub 1 (3, -1, 5)” e o segundo é rotulado como “P sub 2 (2, 1, -1)”. Há um segmento de linha entre os dois pontos. — Figura$\PageIndex{7}$: Encontre a distância entre os dois pontos.

Solução

Substitua os valores diretamente na fórmula da distância (Equation\ ref {DistanceForm}):

\[\begin{align*} d(P_1,P_2) &=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \\[4pt] &=\sqrt{(2−3)^2+(1−(−1))^2+(−1−5)^2} \\[4pt] &=\sqrt{(-1)^2+2^2+(−6)^2} \\[4pt] &=\sqrt{41}. \end{align*}\]

Exercício$\PageIndex{2}$

Encontre a distância entre os pontos$P_1=(1,−5,4)$$P_2=(4,−1,−1)$ e.

Dica: $d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}$
Responda: $5\sqrt{2}$

Antes de passar para a próxima seção, vamos ter uma ideia de como é$ℝ^3$ diferente de$ℝ^2$. Por exemplo, em$ℝ^2$, linhas que não são paralelas devem sempre se cruzar. Esse não é o caso em$ℝ^3$. Por exemplo, considere as linhas mostradas na Figura$\PageIndex{8}$. Essas duas linhas não são paralelas nem se cruzam.

Figura$\PageIndex{8}$: Essas duas linhas não são paralelas, mas ainda não se cruzam.

Você também pode ter círculos que estão interconectados, mas não têm pontos em comum, como na Figura$\PageIndex{9}$.

Figura$\PageIndex{9}$: Esses círculos estão interconectados, mas não têm pontos em comum.

Temos muito mais flexibilidade trabalhando em três dimensões do que quando trabalhamos com apenas duas dimensões.

Escrevendo equações em$ℝ^3$

Agora que podemos representar pontos no espaço e determinar a distância entre eles, podemos aprender a escrever equações de objetos geométricos, como linhas, planos e superfícies curvas$ℝ^3$. Primeiro, começamos com uma equação simples. Compare os gráficos da equação$x=0$ em$ℝ$$ℝ^2$, e$ℝ^3$ (Figura$\PageIndex{10}$). A partir desses gráficos, podemos ver que a mesma equação pode descrever um ponto, uma linha ou um plano.

Esta figura tem três imagens. O primeiro é um eixo horizontal com um ponto desenhado em 0. O segundo é o plano de coordenadas cartesiano bidimensional. O terceiro é o sistema de coordenadas tridimensional. Ele está dentro de uma caixa e tem uma grade desenhada no plano y z. — Figura$\PageIndex{10}$: (a) Em$ℝ$, a equação$x=0$ descreve um único ponto. (b) Em$ℝ^2$, a equação$x=0$ descreve uma linha, o$y$ eixo. (c) Em$ℝ^3$, a equação$x=0$ descreve um plano, o$yz$ plano.

No espaço, a equação$x=0$ descreve todos os pontos$(0,y,z)$. Essa equação define o$yz$ plano. Da mesma forma, o$xy$ plano -contém todos os pontos do formulário$(x,y,0)$. A equação$z=0$ define o $xy$plano -e a equação$y=0$ descreve o$xz$ plano -( Figura$\PageIndex{11}$).

Esta figura tem duas imagens. O primeiro é o sistema de coordenadas tridimensional. Ele está dentro de uma caixa e tem uma grade desenhada no plano x y. O segundo é o sistema de coordenadas tridimensional. Ele está dentro de uma caixa e tem uma grade desenhada no plano x z. — Figura$\PageIndex{11}$: (a) No espaço, a equação$z=0$ descreve o$xy$ plano. (b) Todos os pontos no$xz$ plano C satisfazem a equação$y=0$.

Entender as equações dos planos coordenados nos permite escrever uma equação para qualquer plano que seja paralelo a um dos planos coordenados. Quando um plano é paralelo ao $xy$plano -, por exemplo, a coordenada$z$ - de cada ponto no plano tem o mesmo valor constante. Somente as coordenadas$x$ $y$- e - dos pontos nesse plano variam de ponto a ponto.

Equações de planos paralelos a planos coordenados

O plano no espaço que é paralelo ao$xy$ plano -e contém o ponto$(a,b,c)$ pode ser representado pela equação$z=c$.
O plano no espaço que é paralelo ao$xz$ plano -e contém o ponto$(a,b,c)$ pode ser representado pela equação$y=b$.
O plano no espaço que é paralelo ao$yz$ plano -e contém o ponto$(a,b,c)$ pode ser representado pela equação$x=a$.

Exemplo$\PageIndex{3}$: Writing Equations of Planes Parallel to Coordinate Planes

Escreva uma equação do plano passando por um ponto$(3,11,7)$ que é paralelo ao$yz$ plano.
Encontre uma equação do plano passando por pontos$(6,−2,9), (0,−2,4),$ e$(1,−2,−3).$

Solução

Quando um plano é paralelo ao$yz$ plano -, somente as$z$ coordenadas $y$- e -podem variar. A$x$ coordenada -tem o mesmo valor constante para todos os pontos nesse plano, então esse plano pode ser representado pela equação$x=3$.
Cada um dos pontos$(6,−2,9), (0,−2,4),$$(1,−2,−3)$ tem a mesma$y$ coordenada. Esse plano pode ser representado pela equação$y=−2$.

Exercício$\PageIndex{3}$

Escreva uma equação do plano passando por um ponto$(1,−6,−4)$ que é paralelo ao$xy$ plano.

Dica: Se um plano for paralelo ao$xy$ plano -, as coordenadas z dos pontos nesse plano não variam.
Responda: $z=−4$

Como vimos, na$ℝ^2$ equação$x=5$ descreve a linha vertical passando pelo ponto$(5,0)$. Essa linha é paralela ao$y$ eixo -. Em uma extensão natural, a equação$x=5$ em$ℝ^3$ descreve o plano que passa pelo ponto$(5,0,0)$, que é paralelo ao $yz$plano. Outra extensão natural de uma equação familiar é encontrada na equação de uma esfera.

Definição: Esfera

Uma esfera é o conjunto de todos os pontos no espaço equidistantes de um ponto fixo, o centro da esfera (Figura$\PageIndex{12}$), assim como o conjunto de todos os pontos em um plano que estão equidistantes do centro representa um círculo. Em uma esfera, como em um círculo, a distância do centro até um ponto na esfera é chamada de raio.

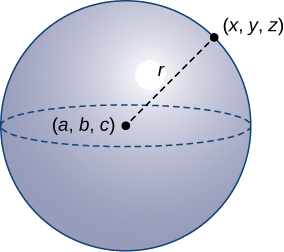
Essa imagem é uma esfera. Tem centro em (a, b, c) e tem um raio representado por uma linha quebrada do ponto central (a, b, c) até a borda da esfera em (x, y, z). O raio é rotulado como “r”. — Figura$\PageIndex{12}$: Cada ponto$(x,y,z)$ na superfície de uma esfera está a$r$ unidades de distância do centro$(a,b,c)$.

A equação de um círculo é derivada usando a fórmula da distância em duas dimensões. Da mesma forma, a equação de uma esfera é baseada na fórmula tridimensional da distância.

Equação padrão de uma esfera

A esfera com centro$(a,b,c)$ e raio$r$ pode ser representada pela equação

\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]

Essa equação é conhecida como a equação padrão de uma esfera.

Exemplo$\PageIndex{4}$: Finding an Equation of a Sphere

Encontre a equação padrão da esfera com centro$(10,7,4)$ e ponto$(−1,3,−2)$, conforme mostrado na Figura$\PageIndex{13}$.

Figura$\PageIndex{13}$: A esfera centrada no ponto de$(10,7,4)$ contenção$(−1,3,−2).$

Solução

Use a fórmula da distância para encontrar o raio$r$ da esfera:

\[\begin{align*} r &=\sqrt{(−1−10)^2+(3−7)^2+(−2−4)^2} \\[4pt] &=\sqrt{(−11)^2+(−4)^2+(−6)^2} \\[4pt] &=\sqrt{173} \end{align*} \nonumber \]

A equação padrão da esfera é

\[(x−10)^2+(y−7)^2+(z−4)^2=173. \nonumber \]

Exercício$\PageIndex{4}$

Encontre a equação padrão da esfera com o centro$(−2,4,−5)$ contendo o ponto$(4,4,−1).$

Dica: Primeiro, use a fórmula da distância para encontrar o raio da esfera.
Responda: \[(x+2)^2+(y−4)^2+(z+5)^2=52 \nonumber \]

Exemplo$\PageIndex{5}$: Finding the Equation of a Sphere

Deixe$P=(−5,2,3)$ e$Q=(3,4,−1)$, e suponha que o segmento de linha$\overline{PQ}$ forme o diâmetro de uma esfera (Figura$\PageIndex{14}$). Encontre a equação da esfera.

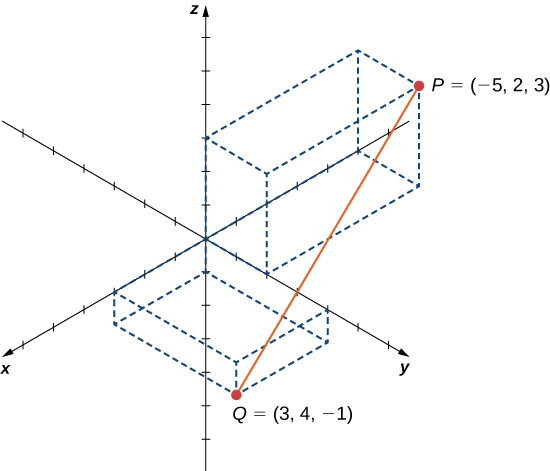
Esta figura é o sistema de coordenadas tridimensional. Há dois pontos rotulados. O primeiro ponto é P = (-5, 2, 3). O segundo ponto é Q = (3, 4, -1). Há um segmento de linha desenhado entre os dois pontos. — Figura$\PageIndex{14}$: Segmento de linha$\overline{PQ}$.

Solução:

Como$\overline{PQ}$ é o diâmetro da esfera, sabemos que o centro da esfera é o ponto médio de$\overline{PQ}$. Então,

\[C=\left(\dfrac{−5+3}{2},\dfrac{2+4}{2},\dfrac{3+(−1)}{2}\right)=(−1,3,1). \nonumber \]

Além disso, sabemos que o raio da esfera é metade do comprimento do diâmetro. Isso dá

\[\begin{align*} r &=\dfrac{1}{2}\sqrt{(−5−3)^2+(2−4)^2+(3−(−1))^2} \\[4pt] &=\dfrac{1}{2}\sqrt{64+4+16} \\[4pt] &=\sqrt{21} \end{align*}\]

Então, a equação da esfera é$(x+1)^2+(y−3)^2+(z−1)^2=21.$

Exercício$\PageIndex{5}$

Encontre a equação da esfera com diâmetro$\overline{PQ}$, onde$P=(2,−1,−3)$ e$Q=(−2,5,−1).$

Dica: Encontre primeiro o ponto médio do diâmetro.
Responda: \[x^2+(y−2)^2+(z+2)^2=14 \nonumber \]

Exemplo$\PageIndex{6}$: Graphing Other Equations in Three Dimensions

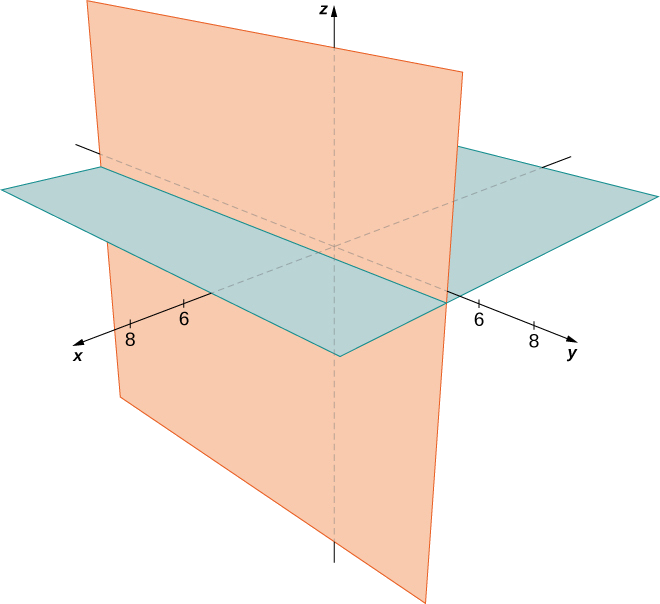
Descreva o conjunto de pontos que satisfaz$(x−4)(z−2)=0,$ e represente graficamente o conjunto.

Solução

Devemos ter um$x−4=0$ ou$z−2=0$, então o conjunto de pontos forma os dois planos$x=4$ e$z=2$ (Figura$\PageIndex{15}$).

Esta figura é o sistema de coordenadas tridimensional. Tem dois planos de interseção desenhados. O primeiro é o plano x y. O segundo é o plano y z. Eles são perpendiculares entre si. — Figura$\PageIndex{15}$: O conjunto de pontos satisfatórios$(x−4)(z−2)=0$ forma os dois planos$x=4$$z=2$ e.

Exercício$\PageIndex{6}$

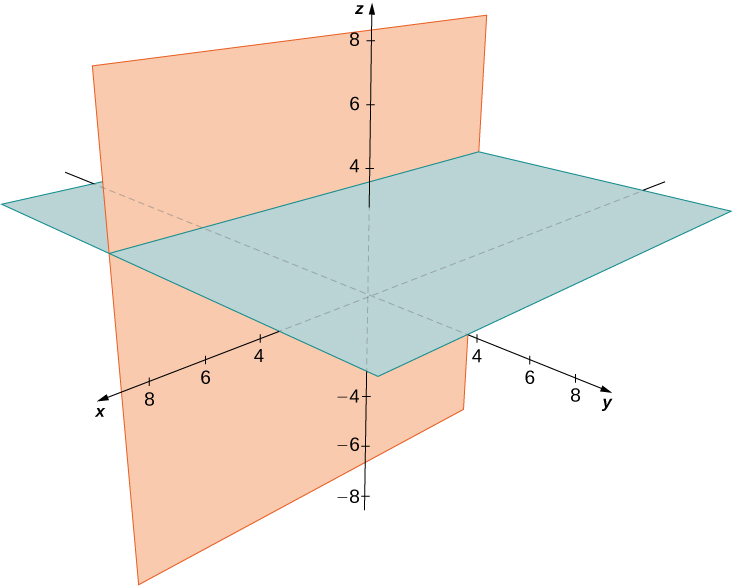
Descreva o conjunto de pontos que satisfaz$(y+2)(z−3)=0,$ e represente graficamente o conjunto.

Dica

Um dos fatores deve ser zero.

Responda

O conjunto de pontos forma os dois planos$y=−2$$z=3$ e.

$Esta figura é o sistema de coordenadas tridimensional. Tem dois planos de interseção desenhados. O primeiro é o plano x z. O segundo é paralelo ao plano y z no valor de z = 3. Eles são perpendiculares entre si.$

Exemplo$\PageIndex{7}$: Graphing Other Equations in Three Dimensions

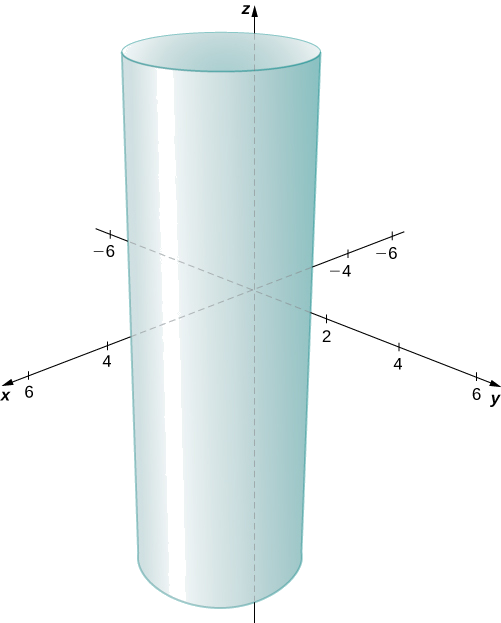
Descreva o conjunto de pontos no espaço tridimensional que satisfaz$(x−2)^2+(y−1)^2=4,$ e represente graficamente o conjunto.

Solução

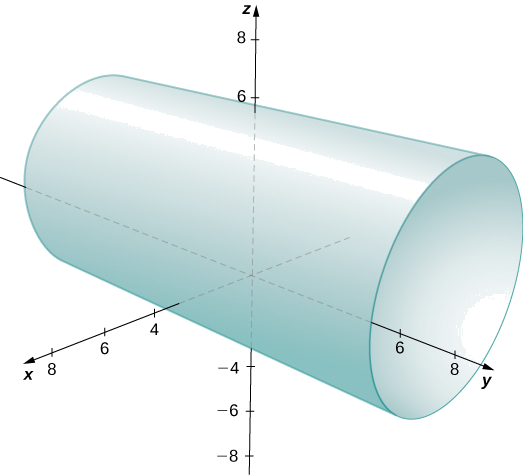
As $y$coordenadas$x$ - e -formam um círculo no $xy$plano -do raio$2$, centrado em$(2,1)$. Como não há restrição na $z$coordenada -, o resultado tridimensional é um cilindro circular de raio$2$ centrado na linha com$x=2$$y=1$ e. O cilindro se estende indefinidamente na$z$ direção -( Figura$\PageIndex{16}$).

Esta figura é o sistema de coordenadas tridimensional. Tem um cilindro vertical paralelo ao eixo z e centrado em torno da linha paralela ao eixo z com x = 2 e y = 1. — Figura$\PageIndex{16}$: O conjunto de pontos satisfatório$(x−2)^2+(y−1)^2=4$. Este é um cilindro de raio$2$ centrado na linha com$x=2$$y=1$ e.

Exercício$\PageIndex{7}$

Descreva o conjunto de pontos no espaço tridimensional que satisfaz e$x^2+(z−2)^2=16$ represente graficamente a superfície.

Dica

Pense no que acontece se você traçar essa equação em duas dimensões no$xz$ plano -.

Responda

Um cilindro de raio 4 centrado na linha com$x=0$$z=2$ e.

$Esta figura é o sistema de coordenadas tridimensional. Ele tem um cilindro paralelo ao eixo y e centrado em torno do eixo y.$

Trabalhando com vetores em$ℝ^3$

Assim como os vetores bidimensionais, os vetores tridimensionais são quantidades com magnitude e direção e são representados por segmentos de linha direcionados (setas). Com um vetor tridimensional, usamos uma seta tridimensional.

Vetores tridimensionais também podem ser representados na forma de componentes. A notação$\vecs{v}=⟨x,y,z⟩$ é uma extensão natural do caso bidimensional, representando um vetor com o ponto inicial na origem e o ponto terminal$(x,y,z)$.$(0,0,0)$ O vetor zero é$\vecs{0}=⟨0,0,0⟩$. Assim, por exemplo, o vetor tridimensional$\vecs{v}=⟨2,4,1⟩$ é representado por um segmento de linha direcionado de um ponto$(0,0,0)$ a$(2,4,1)$ outro (Figura$\PageIndex{17}$).

Esta figura é o sistema de coordenadas tridimensional. Tem um vetor desenhado. O ponto inicial do vetor é a origem. O ponto terminal do vetor é (2, 4, 1). O vetor é rotulado como “v = <2, 4, 1 — Figura$\PageIndex{17}$:$\vecs{v}=⟨2,4,1⟩$ O vetor é representado por um segmento de linha direcionado de ponto$(0,0,0)$ a ponto$(2,4,1).$

A adição vetorial e a multiplicação escalar são definidas de forma análoga ao caso bidimensional. Se$\vecs{v}=⟨x_1,y_1,z_1⟩$ e$\vecs{w}=⟨x_2,y_2,z_2⟩$ são vetores, e$k$ é um escalar, então

\[\vecs{v}+\vecs{w}=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]

\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩. \nonumber \]

Se$k=−1,$ então$k\vecs{v}=(−1)\vecs{v}$ for escrito como$−\vecs{v}$, e a subtração vetorial for definida por$\vecs{v}−\vecs{w}=\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}$.

Os vetores unitários padrão também se estendem facilmente em três dimensões$\hat{\mathbf i}=⟨1,0,0⟩$$\hat{\mathbf j}=⟨0,1,0⟩$,, e$\hat{\mathbf k}=⟨0,0,1⟩$, e nós os usamos da mesma forma que usamos os vetores unitários padrão em duas dimensões. Assim, podemos representar um vetor$ℝ^3$ das seguintes formas:

\[\vecs{v}=⟨x,y,z⟩=x\hat{\mathbf i}+y\hat{\mathbf j}+z\hat{\mathbf k} \nonumber \].

Exemplo$\PageIndex{8}$: Vector Representations

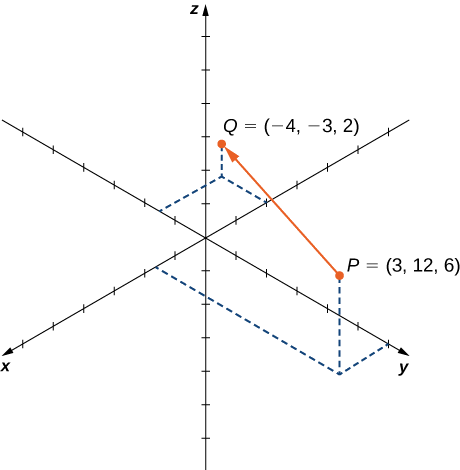
$\vecd{PQ}$Seja o vetor com ponto inicial$P=(3,12,6)$ e ponto terminal$Q=(−4,−3,2)$, conforme mostrado na Figura$\PageIndex{18}$. Expresse$\vecd{PQ}$ na forma de componente e usando vetores unitários padrão.

Esta figura é o sistema de coordenadas tridimensional. Tem dois pontos rotulados. O primeiro ponto é P = (3, 12, 6). O segundo ponto é Q = (-4, -3, 2). Há um vetor de P a Q. — Figura$\PageIndex{18}$: O vetor com ponto inicial$P=(3,12,6)$ e ponto terminal$Q=(−4,−3,2)$.

Solução

Em forma de componente,

\[\begin{align*} \vecd{PQ} =⟨x_2−x_1,y_2−y_1,z_2−z_1⟩ \\[4pt] =⟨−4−3,−3−12,2−6⟩ \\[4pt] =⟨−7,−15,−4⟩. \end{align*}\]

Na forma de unidade padrão,

\[\vecd{PQ}=−7\hat{\mathbf i}−15\hat{\mathbf j}−4\hat{\mathbf k}. \nonumber \]

Exercício$\PageIndex{8}$

Deixe$S=(3,8,2)$$T=(2,−1,3)$ e. Expresse$\vec{ST}$ em forma de componente e em forma de unidade padrão.

Dica: Escreva primeiro$\vecd{ST}$ na forma de componente. $T$é o ponto terminal de$\vecd{ST}$.
Responda: $\vecd{ST}=⟨−1,−9,1⟩=−\hat{\mathbf i}−9\hat{\mathbf j}+\hat{\mathbf k}$

Conforme descrito anteriormente, vetores em três dimensões se comportam da mesma forma que vetores em um plano. A interpretação geométrica da adição vetorial, por exemplo, é a mesma no espaço bidimensional e tridimensional (Figura$\PageIndex{19}$).

Essa figura é a primeira octante do sistema de coordenadas tridimensional. Ele tem três vetores na posição padrão. O primeiro vetor é rotulado como “A”. O segundo vetor é rotulado como “B”. O terceiro vetor é rotulado como “A + B.” Esse vetor está entre os vetores A e B. — Figura$\PageIndex{19}$: Para adicionar vetores em três dimensões, seguimos os mesmos procedimentos que aprendemos para duas dimensões.

Já vimos como algumas das propriedades algébricas dos vetores, como adição de vetores e multiplicação escalar, podem ser estendidas para três dimensões. Outras propriedades podem ser ampliadas de forma semelhante. Eles estão resumidos aqui para nossa referência.

Propriedades dos vetores no espaço

$\vecs{w}=⟨x_2,y_2,z_2⟩$Seja$\vecs{v}=⟨x_1,y_1,z_1⟩$ e seja vetores e$k$ seja um escalar.

Multiplicação escalar:\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
Adição de vetores:\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
Subtração vetorial:\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
Magnitude vetorial:\[\|\vecs{v}\|=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
Vetor unitário na direção de$\vecs{v}$:\[\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\|\vecs{v}\|}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{\|\vecs{v}\|},\dfrac{y_1}{\|\vecs{v}\|},\dfrac{z_1}{\|\vecs{v}\|}⟩, \quad \text{if} \, \vecs{v}≠\vecs{0} \nonumber \]

Vimos que a adição vetorial em duas dimensões satisfaz as propriedades inversas comutativas, associativas e aditivas. Essas propriedades das operações vetoriais também são válidas para vetores tridimensionais. A multiplicação escalar de vetores satisfaz a propriedade distributiva e o vetor zero atua como uma identidade aditiva. As provas para verificar essas propriedades em três dimensões são extensões diretas das provas em duas dimensões.

Exemplo$\PageIndex{9}$: Vector Operations in Three Dimensions

Deixe$\vecs{v}=⟨−2,9,5⟩$ e$\vecs{w}=⟨1,−1,0⟩$ (Figura$\PageIndex{20}$). Encontre os seguintes vetores.

$3\vecs{v}−2\vecs{w}$
$5\|\vecs{w}\|$
$\|5 \vecs{w}\|$
Um vetor unitário na direção de$\vecs{v}$

Esta figura é o sistema de coordenadas tridimensional. Ele tem dois vetores na posição padrão. O primeiro vetor é rotulado como “v = <-2, 9, 5 — Figura$\PageIndex{20}$: Os vetores$\vecs{v}=⟨−2,9,5⟩$$\vecs{w}=⟨1,−1,0⟩$ e.

Solução

a. Primeiro, use a multiplicação escalar de cada vetor e depois subtraia:

\[\begin{align*} 3\vecs{v}−2\vecs{w} =3⟨−2,9,5⟩−2⟨1,−1,0⟩ \\[4pt] =⟨−6,27,15⟩−⟨2,−2,0⟩ \\[4pt] =⟨−6−2,27−(−2),15−0⟩ \\[4pt] =⟨−8,29,15⟩. \end{align*}\]

b. Escreva a equação para a magnitude do vetor e, em seguida, use a multiplicação escalar:

\[5\|\vecs{w}\|=5\sqrt{1^2+(−1)^2+0^2}=5\sqrt{2}. \nonumber \]

c. Primeiro, use a multiplicação escalar e, em seguida, determine a magnitude do novo vetor. Observe que o resultado é o mesmo da parte b.:

\[\|5 \vecs{w}\|=∥⟨5,−5,0⟩∥=\sqrt{5^2+(−5)^2+0^2}=\sqrt{50}=5\sqrt{2} \nonumber \]

d. Lembre-se de que, para encontrar um vetor unitário em duas dimensões, dividimos um vetor por sua magnitude. O procedimento é o mesmo em três dimensões:

\[\begin{align*} \dfrac{\vecs{v}}{\|\vecs{v}\|} =\dfrac{1}{\|\vecs{v}\|}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{(−2)^2+9^2+5^2}}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{110}}⟨−2,9,5⟩ \\[4pt] =⟨\dfrac{−2}{\sqrt{110}},\dfrac{9}{\sqrt{110}},\dfrac{5}{\sqrt{110}}⟩ . \end{align*}\]

Exercício$\PageIndex{9}$:

Deixe$\vecs{v}=⟨−1,−1,1⟩$$\vecs{w}=⟨2,0,1⟩$ e. Encontre um vetor unitário na direção de$5\vecs{v}+3\vecs{w}.$

Dica: Comece escrevendo$5\vecs{v}+3\vecs{w}$ em forma de componente.
Responda: $⟨\dfrac{1}{3\sqrt{10}},−\dfrac{5}{3\sqrt{10}},\dfrac{8}{3\sqrt{10}}⟩$

Exemplo$\PageIndex{10}$: Throwing a Forward Pass

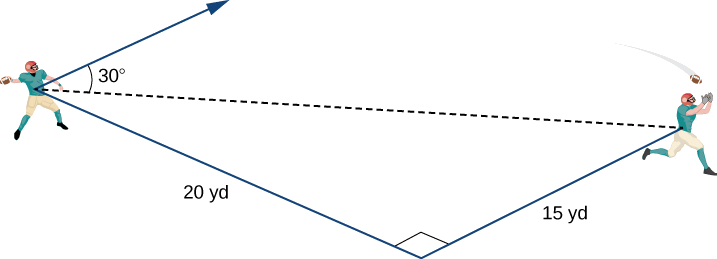
Um zagueiro está parado no campo de futebol se preparando para lançar um passe. Seu receptor está a 20 metros do campo e 15 jardas à esquerda do zagueiro. O zagueiro lança a bola a uma velocidade de 60 mph em direção ao receptor em um ângulo ascendente de$30°$ (veja a figura a seguir). Escreva o vetor de velocidade inicial da bola,$\vecs{v}$, na forma de componente.

$Esta figura é uma imagem de dois jogadores de futebol com o primeiro jogando a bola para o segundo. Há um segmento de linha de cada jogador na parte inferior da imagem. A distância do primeiro jogador até a parte inferior da imagem é de 20 jardas. A distância do segundo jogador até o mesmo ponto na parte inferior da imagem é de 15 jardas. Os dois segmentos de linha são perpendiculares. Há um segmento de linha quebrado do primeiro jogador para o segundo jogador. Há um vetor do primeiro jogador. O ângulo entre a linha quebrada e o vetor é de 30 graus.$

Solução

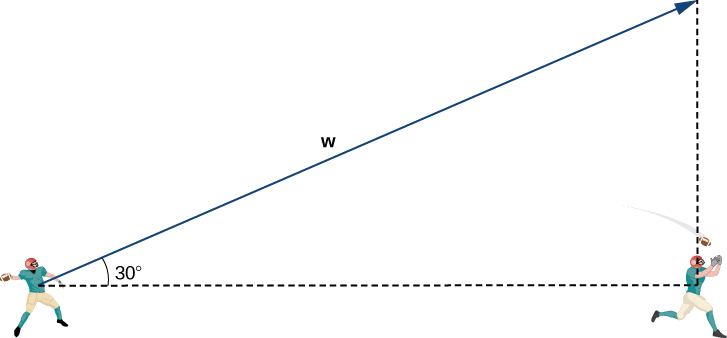
A primeira coisa que queremos fazer é encontrar um vetor na mesma direção do vetor de velocidade da bola. Em seguida, dimensionamos o vetor adequadamente para que ele tenha a magnitude correta. Considere o vetor$\vecs{w}$ que se estende do braço do zagueiro até um ponto diretamente acima da cabeça do receptor em um ângulo de$30°$ (veja a figura a seguir). Esse vetor teria a mesma direção que$\vecs{v}$, mas pode não ter a magnitude correta.

$Esta figura é a imagem de dois jogadores de futebol com o primeiro jogador jogando a bola para o segundo jogador. A distância entre os dois jogadores é representada por um segmento de linha quebrado. Há um vetor do primeiro jogador. O ângulo entre o vetor e o segmento da linha quebrada é de 30 graus. Há um segmento vertical de linha quebrada do segundo jogador. Além disso, há um triângulo reto formado a partir dos dois segmentos de linha quebrados e o vetor do primeiro jogador é rotulado como “w” e é a hipotenusa.$

O receptor está 20 jardas abaixo do campo e 15 jardas à esquerda do zagueiro. Portanto, a distância em linha reta do zagueiro até o receptor é

Dist do QB para o receptor$=\sqrt{15^2+20^2}=\sqrt{225+400}=\sqrt{625}=25$ yd.

Nós temos$\dfrac{25}{\|\vecs{w}\|}=\cos 30°.$ Então, a magnitude de$\vecs{w}$ é dada por

$\|\vecs{w}\|=\dfrac{25}{\cos 30°}=\dfrac{25⋅2}{\sqrt{3}}=\dfrac{50}{\sqrt{3}}$yd

e a distância vertical do receptor até o ponto terminal de$\vecs{w}$ é

Vert dist do receptor ao ponto terminal de$\vecs{w}=\|\vecs{w}\| \sin 30°=\dfrac{50}{\sqrt{3}}⋅\dfrac{1}{2}=\dfrac{25}{\sqrt{3}}$ yd.

Então$\vecs{w}=⟨20,15,\dfrac{25}{\sqrt{3}}⟩$, e tem a mesma direção que$\vecs{v}$.

Lembre-se, porém, de que calculamos a magnitude de$\vecs{w}$ para ser$\|\vecs{w}\|=\dfrac{50}{\sqrt{3}}$ yd e$\vecs{v}$ tem magnitude$60$ mph. Então, precisamos multiplicar o vetor$\vecs{w}$ por uma constante apropriada,$k$. Queremos encontrar um valor de$k$ até$∥k\vecs{w}∥=60$ mph ^*. Nós temos

$\|k \vecs{w}\|=k\|\vecs{w}\|=k\dfrac{50}{\sqrt{3}}$sim,

então queremos

$k \left(\dfrac{50}{\sqrt{3}}\text{ yd}\right) =60$mph

$k=\dfrac{60\sqrt{3}}{50}$mph/yd

$k=\dfrac{6\sqrt{3}}{5}$mph/yd.

Então

$\vecs{v}=k\vecs{w}=k⟨20,15,\dfrac{25}{\sqrt{3}}⟩=\dfrac{6\sqrt{3}}{5}\;⟨20,15,\dfrac{25}{\sqrt{3}}⟩=⟨24\sqrt{3},18\sqrt{3},30⟩$.

Vamos verificar novamente esse$\|\vecs{v}\|=60$ mph. Nós temos

$\|\vecs{v}\|=\sqrt{(24\sqrt{3})^2+(18\sqrt{3})^2+(30)^2}=\sqrt{1728+972+900}=\sqrt{3600}=60$mph.

Então, encontramos os componentes corretos para$\vecs{v}$.

Nota *

Os leitores que estão observando as unidades de medida podem estar se perguntando o que exatamente está acontecendo neste momento: não misturamos apenas jardas e milhas por hora? Não temos, mas o motivo é sutil. Uma maneira de entender isso é perceber que existem realmente dois sistemas de coordenadas paralelas nesse problema: um fornece posições no campo, do outro lado do campo e no ar em unidades de jardas; o outro fornece velocidades no campo, em todo o campo e no ar em unidades de milhas por hora. O vetor$\vecs{w}$ é calculado no sistema de coordenadas de posição; o vetor$\vecs{v}$ estará no sistema de velocidade. Como os eixos correspondentes em cada sistema são paralelos, as direções nos dois sistemas também são paralelas, então a afirmação de que$\vecs{w}$ um$\vecs{v}$ ponto na mesma direção está correta. A constante$k$ que estamos procurando é um fator de conversão entre as magnitudes desses dois vetores, convertendo-se do sistema de posição para o de velocidade no processo. E, como visto acima, nosso cálculo de$k$ produz as unidades certas para essa conversão, ou seja, milhas por hora por jarda.

Exercício$\PageIndex{10}$

Suponha que o quarterback e o receptor estejam no mesmo lugar do exemplo anterior. Desta vez, no entanto, o zagueiro joga a bola a uma velocidade de$40$ mph e um ângulo de$45°$. Escreva o vetor de velocidade inicial da bola,$\vecs{v}$, na forma de componente.

Dica: Siga o processo usado no exemplo anterior.
Responda: $v=⟨16\sqrt{2},12\sqrt{2},20\sqrt{2}⟩$

Conceitos chave

O sistema de coordenadas tridimensional é construído em torno de um conjunto de três eixos que se cruzam em ângulos retos em um único ponto, a origem. Triplos$(x,y,z)$ ordenados são usados para descrever a localização de um ponto no espaço.
A distância$d$ entre os pontos$(x_1,y_1,z_1)$ e$(x_2,y_2,z_2)$ é dada pela fórmula\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}.\nonumber \]
Em três dimensões, as equações$x=a,\, y=b,$ e$z=c$ descrevem planos que são paralelos aos planos coordenados.
A equação padrão de uma esfera com centro$(a,b,c)$ e raio$r$ é\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
Em três dimensões, como em duas, os vetores são comumente expressos na forma de componentes$\vecs v=⟨x,y,z⟩$, ou em termos dos vetores unitários padrão,$\vecs v= x\,\mathbf{\hat i}+y\,\mathbf{\hat j}+z\,\mathbf{\hat k}.$
As propriedades dos vetores no espaço são uma extensão natural das propriedades dos vetores em um plano. $\vecs w=⟨x_2,y_2,z_2⟩$Seja$\vecs v=⟨x_1,y_1,z_1⟩$ e seja vetores e$k$ seja um escalar.

Multiplicação escalar:

\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]

Adição de vetores:

\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]

Subtração vetorial:

\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]

Magnitude vetorial:

\[‖\vecs{v}‖=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]

Vetor unitário na direção de$\vecs{v}$:

\[\dfrac{\vecs{v}}{‖\vecs{v}‖}=\dfrac{1}{‖\vecs{v}‖}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{‖\vecs{v}‖},\dfrac{y_1}{‖\vecs{v}‖},\dfrac{z_1}{‖\vecs{v}‖}⟩, \; \vecs{v}≠\vecs{0} \nonumber \]

Equações chave

Distância entre dois pontos no espaço:

\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \nonumber \]

Esfera com centro$(a,b,c)$ e raio$r$:

\[(x−a)^2+(y−b)^2+(z−c)^2=r^2 \nonumber \]

Glossário

plano coordenado: um plano contendo dois dos três eixos de coordenadas no sistema de coordenadas tridimensional, nomeado pelos eixos que ele contém: o$xy$ plano -,$xz$ -plano ou o$yz$ -plano

regra da mão direita: uma forma comum de definir a orientação do sistema de coordenadas tridimensional; quando a mão direita é curvada em torno do$z$ eixo -de tal forma que os dedos se curvam do$x$ eixo positivo para o positivo$y$, o polegar aponta na direção do$z$ eixo positivo

octantes: as oito regiões do espaço criadas pelos planos coordenados

esfera: o conjunto de todos os pontos equidistantes de um determinado ponto conhecido como centro

equação padrão de uma esfera: $(x−a)^2+(y−b)^2+(z−c)^2=r^2$descreve uma esfera com centro$(a,b,c)$ e raio$r$

sistema de coordenadas retangulares tridimensionais: um sistema de coordenadas definido por três linhas que se cruzam em ângulos retos; cada ponto no espaço é descrito por um triplo ordenado$(x,y,z)$ que traça sua localização em relação aos eixos definidores

Colaboradores

Template:ContribOpenStaxCalc

$\PageIndex{10}$O exemplo foi modificado por Doug Baldwin e Paul Seeburger para esclarecer as unidades de medida que ele usa e como as usa.

Paul Seeburger também criou versões dinâmicas de Figures$\PageIndex{8}, \PageIndex{9}$ e$\PageIndex{13}$ usando o Calcplot3D.

Definição: Sistema de coordenadas retangulares tridimensional

Exemplo\(\PageIndex{1}\): Locating Points in Space

Exercício\(\PageIndex{1}\)