11.4: Área e comprimento do arco em coordenadas polares

Objetivos de

• Aplique a fórmula para a área de uma região em coordenadas polares.
• Determine o comprimento do arco de uma curva polar.

No sistema de coordenadas retangulares, a integral definida fornece uma forma de calcular a área sob uma curva. Em particular, se tivermos uma função\(y=f(x)\) definida de\(x=a\) até\(x=b\) onde\(f(x)>0\) neste intervalo, a área entre a curva e o eixo x é dada por

\[A=\int ^b_af(x)dx. \nonumber \]

Esse fato, junto com a fórmula para avaliar essa integral, está resumido no Teorema Fundamental do Cálculo. Da mesma forma, o comprimento do arco dessa curva é dado por

\[L=\int ^b_a\sqrt{1+(f′(x))^2}dx. \nonumber \]

Nesta seção, estudamos fórmulas análogas para área e comprimento do arco no sistema de coordenadas polares.

Áreas de regiões delimitadas por curvas polares

Estudamos as fórmulas para a área sob uma curva definida em coordenadas retangulares e curvas definidas parametricamente. Agora, voltamos nossa atenção para derivar uma fórmula para a área de uma região delimitada por uma curva polar. Lembre-se de que a prova do Teorema Fundamental do Cálculo usou o conceito de soma de Riemann para aproximar a área sob uma curva usando retângulos. Para curvas polares, usamos a soma de Riemann novamente, mas os retângulos são substituídos por setores de um círculo.

Considere uma curva definida pela função\(r=f(θ),\) em que\(α≤θ≤β.\) Nosso primeiro passo é dividir o intervalo\([α,β]\) em n subintervalos de largura igual. A largura de cada subintervalo é dada pela fórmula\(Δθ=(β−α)/n\) e o i ésimo ponto de partição\(θ_i\) é dado pela fórmula\(θ_i=α+iΔθ\). Cada ponto de partição\(θ=θ_i\) define uma linha com inclinação\(\tan θ_i\) passando pelo polo, conforme mostrado no gráfico a seguir.

Figura\(\PageIndex{1}\): Uma partição de uma curva típica em coordenadas polares.

Os segmentos de linha são conectados por arcos de raio constante. Isso define setores cujas áreas podem ser calculadas usando uma fórmula geométrica. A área de cada setor é então usada para aproximar a área entre segmentos de linha sucessivos. Em seguida, somamos as áreas dos setores para aproximar a área total. Essa abordagem fornece uma aproximação da soma de Riemann para a área total. A fórmula para a área de um setor de um círculo é ilustrada na figura a seguir.

Figura\(\PageIndex{2}\): A área de um setor de um círculo é dada por\(A=\dfrac{1}{2}θr^2\).

Lembre-se de que a área de um círculo é\(A=πr^2\). Ao medir ângulos em radianos, 360 graus é igual a\(2π\) radianos. Portanto, uma fração de um círculo pode ser medida pelo ângulo central\(θ\). A fração do círculo é dada por\(\dfrac{θ}{2π}\), então a área do setor é essa fração multiplicada pela área total:

\[A=(\dfrac{θ}{2π})πr^2=\dfrac{1}{2}θr^2. \nonumber \]

Como o raio de um setor típico na Figura\(\PageIndex{1}\) é dado por\(r_i=f(θ_i)\), a área do setor é dada por

\[A_i=\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Portanto, uma soma de Riemann que se aproxima da área é dada por

\[A_n=\sum_{i=1}^nA_i≈\sum_{i=1}^n\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Tomamos o limite\(n→∞\) para obter a área exata:

\[A=\lim_{n→∞}A_n=\dfrac{1}{2}\int ^β_α(f(θ))^2dθ. \nonumber \]

Isso dá o seguinte teorema.

Área de uma região delimitada por uma curva polar

Suponha que\(f\) seja contínuo e não negativo no intervalo\(α≤θ≤β\) com\(0<β−α≤2π\). A área da região delimitada pelo gráfico\(r=f(θ)\) entre as linhas radiais\(θ=α\) e\(θ=β\) é

\[\begin{align} A =\dfrac{1}{2}\int ^β_α[f(θ)]^2 dθ \\[4pt] =\dfrac{1}{2}\int ^β_αr^2 dθ. \label{areapolar}\end{align} \]

Exemplo\(\PageIndex{1}\): Finding an Area of a Polar Region

Encontre a área de uma pétala da rosa definida pela equação\(r=3\sin(2θ).\)

Solução

O gráfico dos\(r=3\sin (2θ)\) seguintes.

Figura\(\PageIndex{3}\): O gráfico de\(r=3\sin (2θ).\)

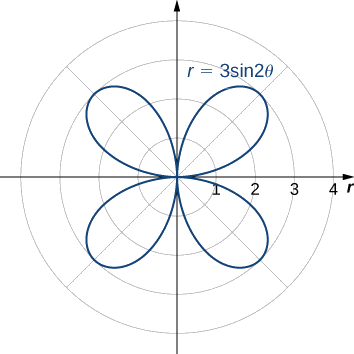
Quando\(θ=0\) temos\(r=3\sin(2(0))=0\). O próximo valor para o qual\(r=0\) é\(θ=π/2\). Isso pode ser visto resolvendo a equação\(3\sin (2θ)=0\) para\(θ\). Portanto, os valores\(θ=0\) para\(θ=π/2\) traçar a primeira pétala da rosa. Para encontrar a área dentro dessa pétala, use a Equação\ ref {areapolar} com\(f(θ)=3\sin (2θ), α=0,\) e\(β=π/2\):

\[\begin{align*} A &=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_0[3\sin (2θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ. \end{align*}\]

Para avaliar essa integral, use a fórmula\(\sin^2α=(1−\cos (2α))/2\) com\(α=2θ:\)

\[\begin{align*} A &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ \\[4pt] &=\dfrac{9}{2}\int ^{π/2}_0\dfrac{(1−\cos(4θ))}{2}dθ \\[4pt] &=\dfrac{9}{4}(\int ^{π/2}_01−\cos(4θ)dθ) \\[4pt] &=\dfrac{9}{4}(θ−\dfrac{\sin(4θ)}{4}∣^{π/2}_0 \\[4pt] &=\dfrac{9}{4}(\dfrac{π}{2}−\dfrac{\sin 2π}{4})−\dfrac{9}{4}(0−\dfrac{\sin 4(0)}{4}) \\[4pt] &=\dfrac{9π}{8}\end{align*}\]

Exercício\(\PageIndex{1}\)

Encontre a área dentro do cardióide definida pela equação\(r=1−\cos θ\).

Dica

Use a Equação\ ref {areapolar}. Certifique-se de determinar os limites corretos de integração antes de avaliar.

Responda

\(A=3π/2\)

O exemplo\(\PageIndex{1}\) envolveu encontrar a área dentro de uma curva. Também podemos usar a Equação\ ref {areapolar} para encontrar a área entre duas curvas polares. No entanto, muitas vezes precisamos encontrar os pontos de interseção das curvas e determinar qual função define a curva externa ou a curva interna entre esses dois pontos.

Exemplo\(\PageIndex{2}\): Finding the Area between Two Polar Curves

Encontre a área fora do cardióide\(r=2+2\sin θ\) e dentro do círculo\(r=6\sin θ\).

Solução

Primeiro, desenhe um gráfico contendo as duas curvas, conforme mostrado.

Figura\(\PageIndex{4}\): A região entre as curvas\(r=2+2\sin θ\) e\(r=6\sin θ.\)

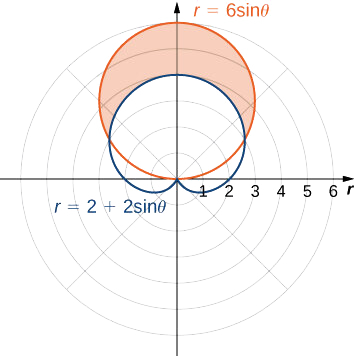
Para determinar os limites da integração, primeiro encontre os pontos de interseção definindo as duas funções iguais uma à outra e resolvendo\(θ\):

\[\begin{align*} 6 \sin θ &=2+2\sin θ \\[4pt] 4\sin θ &=2 \\[4pt] \sin θ &=\dfrac{1}{2} \end{align*}. \nonumber \]

Isso fornece as soluções\(θ=\dfrac{π}{6}\) e\(θ=\dfrac{5π}{6}\) quais são os limites da integração. O círculo\(r=3\sin θ\) é o gráfico vermelho, que é a função externa, e o cardióide\(r=2+2\sin θ\) é o gráfico azul, que é a função interna. Para calcular a área entre as curvas, comece com a área dentro do círculo entre\(θ=\dfrac{π}{6}\) e\(θ=\dfrac{5π}{6}\), em seguida, subtraia a área dentro do cardióide entre\(θ=\dfrac{π}{6}\) e\(θ=\dfrac{5π}{6}\):

\(A=\text{circle}−\text{cardioid}\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}[6\sin θ]^2dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}[2+2\sin θ]^2dθ\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}36\sin^2θ\,dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}4+8\sin θ+4\sin^2θ\,dθ\)

\(=18\int ^{5π/6}_{π/6}\dfrac{1−\cos(2θ)}{2}dθ−2\int ^{5π/6}_{π/6}1+2\sin θ+\dfrac{1−\cos(2θ)}{2}dθ\)

\(=9[θ−\dfrac{\sin(2θ)}{2}]^{5π/6}_{π/6}−2[\dfrac{3θ}{2}−2\cos θ−\dfrac{\sin(2θ)}{4}]^{5π/6}_{π/6}\)

\(=9(\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})−9(\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})−(3(\dfrac{5π}{6})−4\cos\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})+(3(\dfrac{π}{6})−4\cos\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})\)

\(=4π\).

Exercício\(\PageIndex{2}\)

Encontre a área dentro do círculo\(r=4\cos θ\) e fora do círculo\(r=2\).

Dica

Use Equation\ ref {areapolar} e aproveite a simetria.

Responda

\(A=\dfrac{4π}{3}+2\sqrt{3}\)

No exemplo,\(\PageIndex{2}\) encontramos a área dentro do círculo e fora do cardióide encontrando primeiro seus pontos de interseção. Observe que resolver a equação diretamente\(θ\) resultou em duas soluções:\(θ=\dfrac{π}{6}\)\(θ=\dfrac{5π}{6}\) e. No entanto, no gráfico há três pontos de interseção. O terceiro ponto de interseção é a origem. A razão pela qual esse ponto não apareceu como uma solução é porque a origem está em ambos os gráficos, mas para valores diferentes de\(θ\). Por exemplo, para o cardióide, obtemos

\[\begin{align*} 2+2\sin θ =0 \\[4pt] \sin θ =−1 ,\end{align*}. \nonumber \]

então os valores para resolver\(θ\) essa equação são\(θ=\dfrac{3π}{2}+2nπ\), onde\(n\) está qualquer número inteiro. Para o círculo, obtemos

\[6\sin θ=0. \nonumber \]

As soluções para essa equação são da forma\(θ=nπ\) de qualquer valor inteiro de\(n\). Esses dois conjuntos de soluções não têm pontos em comum. Independentemente desse fato, as curvas se cruzam na origem. Esse caso deve sempre ser levado em consideração.

Comprimento do arco em curvas polares

Aqui, derivamos uma fórmula para o comprimento do arco de uma curva definida em coordenadas polares. Em coordenadas retangulares, o comprimento do arco de uma curva parametrizada\((x(t),y(t))\) para\(a≤t≤b\) é dado por

\[L=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dt. \nonumber \]

Nas coordenadas polares, definimos a curva pela equação\(r=f(θ)\), onde\(α≤θ≤β.\) Para adaptar a fórmula do comprimento do arco para uma curva polar, usamos as equações

\[x=r\cos θ=f(θ)\cos θ \nonumber \]

e

\[y=r\sin θ=f(θ)\sin θ, \nonumber \]

e substituímos o parâmetro\(t\) por\(θ\). Então

\[\dfrac{dx}{dθ}=f′(θ)\cos θ−f(θ)\sin θ \nonumber \]

\[\dfrac{dy}{dθ}=f′(θ)\sin θ+f(θ)\cos θ. \nonumber \]

Nós substituímos\(dt\) por\(dθ\), e os limites inferior e superior de integração são\(α\) e\(β\), respectivamente. Então, a fórmula do comprimento do arco se torna

\[ \begin{align*} L &=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \\[4pt] &=\int ^β_α\sqrt{\left(\dfrac{dx}{dθ}\right)^2+\left(\dfrac{dy}{dθ}\right)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ)\cos θ−f(θ)\sin θ)^2+(f′(θ)\sin θ+f(θ)\cos θ)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2(\cos^2 θ+\sin^2 θ)+(f(θ))^2(\cos^2 θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2+(f(θ))^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ \end{align*}\]

Isso nos dá o seguinte teorema.

Comprimento do arco de uma curva definida por uma função polar

\(f\)Seja uma função cuja derivada é contínua em um intervalo\(α≤θ≤β\). O comprimento do gráfico\(r=f(θ)\) de\(θ=α\) a\(θ=β\) é

\[ \begin{align} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \label{arcpolar1} \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ. \label{arcpolar2} \end{align} \]

Exemplo\(\PageIndex{3}\): Finding the Arc Length of a cardioid

Encontre o comprimento do arco do cardióide\(r=2+2\cos θ\).

Solução

Quando\(θ=0,r=2+2\cos 0 =4.\) Além disso, como\(θ\) vai de\(0\) para\(2π\), o cardióide é rastreado exatamente uma vez. Portanto, esses são os limites da integração. Usando\(f(θ)=2+2\cos θ, α=0,\) uma\(β=2π,\) equação\ ref {arcpolar1} se torna

\[\begin{align*} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{[2+2\cos θ]^2+[−2\sin θ]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4\cos^2θ+4\sin^2θ}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4(\cos^2θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{8+8\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ. \end{align*}\]

Em seguida, usando a identidade,\(\cos(2α)=2\cos^2α−1,\) adicione 1 aos dois lados e multiplique por 2. Isso dá\(2+2\cos(2α)=4\cos^2α.\) Substituindo\(α=θ/2\) dá\(2+2\cos θ=4\cos^2(θ/2)\), então a integral se torna

\[\begin{align*} L &= 2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{4\cos^2(\dfrac{θ}{2})}\,dθ \\[4pt] &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ.\end{align*}\]

O valor absoluto é necessário porque o cosseno é negativo para alguns valores em seu domínio. Para resolver esse problema, altere os limites de\(0\) para\(π\) e duplique a resposta. Essa estratégia funciona porque o cosseno é positivo entre\(0\)\(\dfrac{π}{2}\) e. Assim,

\[\begin{align*} L &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ \\[4pt] &=8\int ^π_0 \cos(\dfrac{θ}{2})\,dθ \\[4pt] &=8(2\sin(\dfrac{θ}{2})∣^π_0 \\[4pt] &=16\end{align*}\]

Exercício\(\PageIndex{3}\)

Encontre o comprimento total do arco de\(r=3\sin θ\).

Dica

Use a Equação\ ref {arcpolar1}. Para determinar os limites corretos, faça uma tabela de valores.

Responda

\(s=3π\)

Conceitos-chave

• A área de uma região em coordenadas polares definida pela equação\(r=f(θ)\) com\(α≤θ≤β\) é dada pela integral\(A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\).
• Para encontrar a área entre duas curvas no sistema de coordenadas polares, primeiro encontre os pontos de interseção e subtraia as áreas correspondentes.
• O comprimento do arco de uma curva polar definida pela equação\(r=f(θ)\) com\(α≤θ≤β\) é dado pela integral\(L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ\).

Equações-chave

• Área de uma região delimitada por uma curva polar\[A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ=\dfrac{1}{2}\int ^β_αr^2dθ \nonumber \]
• Comprimento do arco de uma curva polar\[L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ \nonumber \]