11.3: Coordenadas polares
- Page ID
- 187890
- Localize pontos em um plano usando coordenadas polares.
- Converta pontos entre coordenadas retangulares e polares.
- Esboce curvas polares a partir de determinadas equações.
- Converta equações entre coordenadas retangulares e polares.
- Identifique a simetria em curvas e equações polares.
O sistema de coordenadas retangulares (ou plano cartesiano) fornece um meio de mapear pontos para pares ordenados e pares ordenados para pontos. Isso é chamado de mapeamento individual de pontos no plano para pares ordenados. O sistema de coordenadas polares fornece um método alternativo de mapeamento de pontos para pares ordenados. Nesta seção, vemos que, em algumas circunstâncias, as coordenadas polares podem ser mais úteis do que as coordenadas retangulares.
Definindo coordenadas polares
Para encontrar as coordenadas de um ponto no sistema de coordenadas polares, considere a Figura\(\PageIndex{1}\). O ponto\(P\) tem coordenadas cartesianas\((x,y)\). O segmento de linha que conecta a origem ao ponto\(P\) mede a distância da origem\(P\) e tem comprimento\(r\). O ângulo entre o eixo x positivo e o segmento da linha tem medida\(θ\). Essa observação sugere uma correspondência natural entre o par de coordenadas\((x,y)\) e os valores\(r\)\(θ\) e. Essa correspondência é a base do sistema de coordenadas polares. Observe que cada ponto no plano cartesiano tem dois valores (daí o termo par ordenado) associados a ele. No sistema de coordenadas polares, cada ponto também tem dois valores associados a ele:\(r\)\(θ\) e.
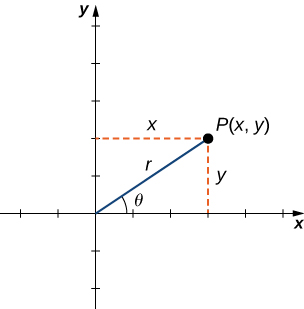
Usando a trigonometria do trigonometria do triângulo reto, as seguintes equações são verdadeiras para o ponto\(P\):
\[\cos θ=\dfrac{x}{r}\text{ so }x=r\cos θ \nonumber \]
\[\sin θ=\dfrac{y}{r}\text{ so }y=r\sin θ. \nonumber \]
Além disso,
\[r^2=x^2+y^2 \nonumber \]
e
\[\tan θ=\dfrac{y}{x}. \nonumber \]
Cada ponto\((x,y)\) no sistema de coordenadas cartesianas pode, portanto, ser representado como um par ordenado\((r,θ)\) no sistema de coordenadas polares. A primeira coordenada é chamada de coordenada radial e a segunda coordenada é chamada de coordenada angular. Cada ponto no plano pode ser representado dessa forma.
Observe que a equação\(\tan θ=y/x\) tem um número infinito de soluções para qualquer par ordenado\((x,y)\). No entanto, se restringirmos as soluções a valores entre\(0\) e\(2π\), então, podemos atribuir uma solução exclusiva ao quadrante em que o ponto original\((x,y)\) está localizado. Então, o valor correspondente de\(r\) é positivo, então\(r^2=x^2+y^2\).
Dado um ponto\(P\) no plano com coordenadas cartesianas\((x,y)\) e coordenadas polares\((r,θ)\), as seguintes fórmulas de conversão são verdadeiras:
\[\begin{align} x &=r\cos θ \label{eq1} \\[4pt] y &=r\sin θ \label{eq2}\end{align} \]
e
\[\begin{align} r^2 &= x^2+y^2 \label{eq3}\\[4pt] \tan θ &=\dfrac{y}{x} \label{eq4}\end{align}. \]
Essas fórmulas podem ser usadas para converter coordenadas retangulares em polares ou polares em retangulares. Observe que a Equação\ ref {eq3} é o teorema de Pitágoras. (Figura\(\PageIndex{1}\)).
Converta cada um dos seguintes pontos em coordenadas polares.
- \((1,1)\)
- \((−3,4)\)
- \((0,3)\)
- \((5\sqrt{3},−5)\)
Converta cada um dos seguintes pontos em coordenadas retangulares.
- \((3,π/3)\)
- \((2,3π/2)\)
- \((6,−5π/6)\)
Solução
a. Use\(x=1\) e\(y=1\) na Equação\ ref {eq3}:
\[\begin{align*} r^2 &=x^2+y^2 \\[4pt] &=1^2+1^2 \\ r &=\sqrt{2} \end{align*} \nonumber \]
e via Equation\ ref {eq4}
\[\begin{align*} \tan θ &= \dfrac{y}{x} = \dfrac{1}{1}=1 \\[4pt] θ &=\dfrac{π}{4}. \end{align*}\]
Portanto, esse ponto pode ser representado como\((\sqrt{2},\dfrac{π}{4})\) em coordenadas polares.
b. Use\(x=−3\) e\(y=4\) na Equação\ ref {eq3}:
\[\begin{align*} r^2 &= x^2+y^2=(−3)^2+(4)^2 \\[4pt] r&=5 \end{align*}\]
e via Equation\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=−\dfrac{4}{3}\)
\(θ=\arctan(-\dfrac{4}{3})+π≈2.21.\)
Portanto, esse ponto pode ser representado como\((5,2.21)\) em coordenadas polares.
c. Use\(x=0\) e\(y=3\) na Equação\ ref {eq3}:
\(r^2=x^2+y^2=(3)^2+(0)^2=9+0\)\(r=3\)
e via Equation\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{3}{0}\).
A aplicação direta da segunda equação leva à divisão por zero. Representar graficamente o ponto\((0,3)\) no sistema de coordenadas retangulares revela que o ponto está localizado no eixo y positivo. O ângulo entre o eixo x positivo e o eixo y positivo é\(\dfrac{π}{2}\). Portanto, esse ponto pode ser representado como\((3,\dfrac{π}{2})\) em coordenadas polares.
d. Use\(x=5\sqrt{3}\) e\(y=−5\) na Equação\ ref {eq3}:
\(r^2=x^2+y^2=(5\sqrt{3})^2+(−5)^2=75+25\)
\(r=10\)
e via Equation\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{−5}{5\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\)
\(θ=−\dfrac{π}{6}\).
Portanto, esse ponto pode ser representado como\((10,−\dfrac{π}{6})\) em coordenadas polares.
e. Use\(r=3\) e\(θ=\dfrac{π}{3}\) na Equação\ ref {eq1}:
\(x=r\cos θ=3\cos(\dfrac{π}{3})=3(\dfrac{1}{2})=\dfrac{3}{2}\)
e
\(y=r\sin θ=3\sin(\dfrac{π}{3})=3(\dfrac{\sqrt{3}}{2})=\dfrac{3\sqrt{3}}{2}\).
Portanto, esse ponto pode ser representado como\((\dfrac{3}{2},\dfrac{3\sqrt{3}}{2})\) em coordenadas retangulares.
f. Use\(r=2\) e\(θ=\dfrac{3π}{2}\) na Equação\ ref {eq1}:
\(x=r\cos θ=2\cos(\dfrac{3π}{2})=2(0)=0\)
e
\(y=r\sin θ=2\sin(\dfrac{3π}{2})=2(−1)=−2.\)
Portanto, esse ponto pode ser representado como\((0,−2)\) em coordenadas retangulares.
g. Use\(r=6\) e\(θ=−\dfrac{5π}{6}\) na Equação\ ref {eq1}:
\(x=r\cos θ=6\cos(−\dfrac{5π}{6})=6(−\dfrac{\sqrt{3}}{2})=−3\sqrt{3}\)
e
\(y=r\sin θ=6\sin(−\dfrac{5π}{6})=6(−\dfrac{1}{2})=−3\).
Portanto, esse ponto pode ser representado como\((−3\sqrt{3},−3)\) em coordenadas retangulares.
Converta\((−8,−8)\) em coordenadas polares e\((4,\dfrac{2π}{3})\) em coordenadas retangulares.
- Dica
-
Use a Equação\ ref {eq3} e a Equação\ ref {eq1}. Certifique-se de verificar o quadrante ao calcular\(θ\).
- Resposta
-
\((8\sqrt{2},\dfrac{5π}{4})\)e\((−2,2\sqrt{3})\)
A representação polar de um ponto não é única. Por exemplo, as coordenadas polares\((2,\dfrac{π}{3})\) e\((2,\dfrac{7π}{3})\) ambas representam o ponto\((1,\sqrt{3})\) no sistema retangular. Além disso, o valor de r pode ser negativo. Portanto, o ponto com coordenadas polares\((−2,\dfrac{4π}{3})\) também representa o ponto\((1,\sqrt{3})\) no sistema retangular, como podemos ver usando a Equação\ ref {eq1}:
\[x=r\cos θ=−2\cos(\dfrac{4π}{3})=−2(−\dfrac{1}{2})=1 \nonumber \]
e
\[y=r\sin θ=−2\sin(\dfrac{4π}{3})=−2(−\dfrac{\sqrt{3}}{2})=\sqrt{3}. \nonumber \]
Cada ponto no plano tem um número infinito de representações em coordenadas polares. No entanto, cada ponto no plano tem apenas uma representação no sistema de coordenadas retangulares.
Observe que a representação polar de um ponto no plano também tem uma interpretação visual. Em particular,\(r\) é a distância direcionada que o ponto se encontra da origem e\(θ\) mede o ângulo que o segmento de linha da origem até o ponto faz com o\(x\) eixo positivo. Os ângulos positivos são medidos no sentido anti-horário e os ângulos negativos são medidos no sentido horário. O sistema de coordenadas polares aparece na Figura\(\PageIndex{2}\).
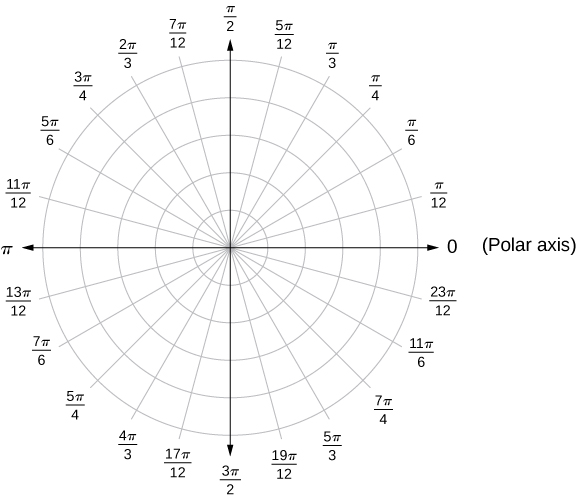
O segmento de linha partindo do centro do gráfico indo para a direita (chamado eixo x positivo no sistema cartesiano) é o eixo polar. O ponto central é o polo, ou origem, do sistema de coordenadas e corresponde\(r=0\) a. O círculo mais interno mostrado na Figura\(\PageIndex{2}\) contém todos os pontos a uma distância de 1 unidade do polo e é representado pela equação\(r=1\). Então\(r=2\) é o conjunto de pontos a 2 unidades do pólo, e assim por diante. Os segmentos de linha que emanam do polo correspondem a ângulos fixos. Para traçar um ponto no sistema de coordenadas polares, comece com o ângulo. Se o ângulo for positivo, meça o ângulo do eixo polar no sentido anti-horário. Se for negativo, meça no sentido horário. Se o valor de r for positivo, mova essa distância ao longo do raio terminal do ângulo. Se for negativo, mova-se ao longo do raio que está oposto ao raio terminal do ângulo dado.
Faça um gráfico de cada um dos seguintes pontos no plano polar.
- \((2,\dfrac{π}{4})\)
- \((−3,\dfrac{2π}{3})\)
- \((4,\dfrac{5π}{4})\)
Solução
Os três pontos estão representados graficamente na Figura\(\PageIndex{3}\).

Trama\((4,\dfrac{5π}{3})\) e\((−3,−\dfrac{7π}{2})\) no plano polar.
- Dica
-
Comece com\(θ\) e depois use\(r\).
- Resposta
-

Curvas polares
Agora que sabemos como traçar pontos no sistema de coordenadas polares, podemos discutir como traçar curvas. No sistema de coordenadas retangulares, podemos representar graficamente uma função\(y=f(x)\) e criar uma curva no plano cartesiano. De forma semelhante, podemos representar graficamente uma curva gerada por uma função\(r=f(θ)\).
A ideia geral por trás de representar graficamente uma função em coordenadas polares é a mesma de representar graficamente uma função em coordenadas retangulares. Comece com uma lista de valores para a variável independente (\(θ\)nesse caso) e calcule os valores correspondentes da variável dependente\(r\). Esse processo gera uma lista de pares ordenados, que podem ser plotados no sistema de coordenadas polares. Por fim, conecte os pontos e aproveite os padrões que possam aparecer. A função pode ser periódica, por exemplo, o que indica que somente um número limitado de valores para a variável independente é necessário.
- Crie uma tabela com duas colunas. A primeira coluna é para\(θ\) e a segunda coluna é para\(r\).
- Crie uma lista de valores para\(θ\).
- Calcule os\(r\) valores correspondentes para cada um\(θ\).
- Faça um gráfico de cada par ordenado\((r,θ)\) nos eixos de coordenadas.
- Conecte os pontos e procure um padrão.
Faça um gráfico da curva definida pela função\(r=4\sin θ\). Identifique a curva e reescreva a equação em coordenadas retangulares.
Solução
Como a função é um múltiplo de uma função senoidal, ela é periódica com período\(2π\), então use valores\(θ\) entre\(0\)\(2π\) e. O resultado das etapas 1 a 3 aparece na tabela a seguir. A figura\(\PageIndex{4}\) mostra o gráfico com base nessa tabela.
| \(θ\) | \(r=4\sin θ\) | \(θ\) | \(r=4\sin θ\) |
|---|---|---|---|
| \ (θ\)” style="alinhamento vertical: médio; ">0 | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">0 | \ (θ\)” style="alinhamento vertical: meio; ">\(π\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">0 |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{π}{6}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">2 | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{7π}{6}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(-2\) |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{π}{4}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(2\sqrt{2}≈2.8\) | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{5π}{4}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(−2\sqrt{2}≈−2.8\) |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{π}{3}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(2\sqrt{3}≈3.4\) | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{4π}{3}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(−2\sqrt{3}≈−3.4\) |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{π}{2}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">4 | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{3π}{2}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(-4\) |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{2π}{3}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(2\sqrt{3}≈3.4\) | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{5π}{3}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(−2\sqrt{3}≈−3.4\) |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{3π}{4}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(2\sqrt{2}≈2.8\) | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{7π}{4}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">\(−2\sqrt{2}≈−2.8\) |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{5π}{6}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">2 | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{11π}{6}\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">−2 |
| \ (θ\)” style="alinhamento vertical: meio; "> | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; "> | \ (θ\)” style="alinhamento vertical: meio; ">\(2π\) | \ (r=4\ sin θ\)” style="alinhamento vertical: médio; ">0 |
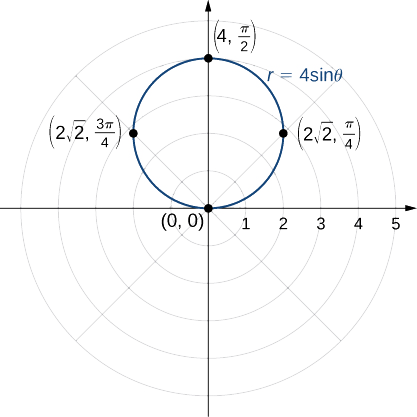
Este é o gráfico de um círculo. A equação\(r=4\sin θ\) pode ser convertida em coordenadas retangulares multiplicando-se primeiro os dois lados por\(r\). Isso fornece a equação.\(r^2=4r\sin θ.\) Em seguida, use os fatos de que\(r^2=x^2+y^2\)\(y=r\sin θ\) e. Isso dá\(x^2+y^2=4y\). Para colocar essa equação na forma padrão, subtraia\(4y\) dos dois lados da equação e complete o quadrado:
\[\begin{align*} x^2+y^2−4y &= 0 \\[4pt] x^2+(y^2−4y) &= 0 \\[4pt] x^2+(y^2−4y+4) &= 0+4 \\[4pt] x^2+(y−2)^2&=4 \end{align*}\]
Essa é a equação de uma circunferência com raio 2 e centro\((0,2)\) no sistema de coordenadas retangulares.
Crie um gráfico da curva definida pela função\(r=4+4\cos θ\).
- Dica
-
Siga a estratégia de resolução de problemas para criar um gráfico em coordenadas polares.
- Resposta
-
O nome dessa forma é cardióide, que estudaremos mais adiante nesta seção.
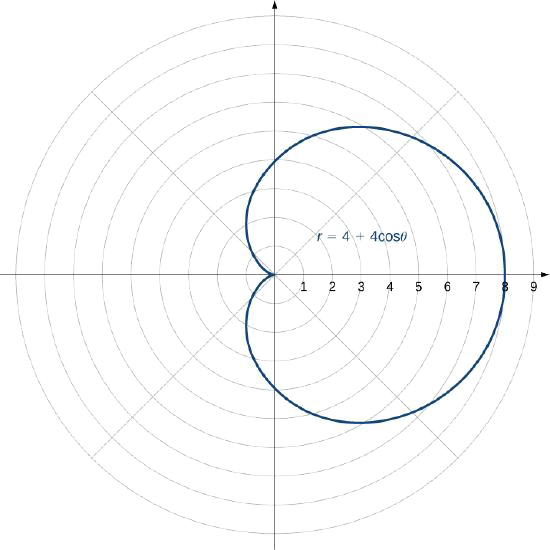
O gráfico em Example\(\PageIndex{3}\) era o de um círculo. A equação da circunferência pode ser transformada em coordenadas retangulares usando as fórmulas de transformação de coordenadas em Equation\ ref {eq1}. \(\PageIndex{4}\)O exemplo fornece mais alguns exemplos de funções para transformar coordenadas polares em retangulares.
Reescreva cada uma das seguintes equações em coordenadas retangulares e identifique o gráfico.
- \(θ=\dfrac{π}{3}\)
- \(r=3\)
- \(r=6\cos θ−8\sin θ\)
Solução:
a. Pegue a tangente de ambos os lados. Isso dá\(\tan θ=\tan(π/3)=\sqrt{3}\). Já que\(\tan θ=y/x\) podemos substituir o lado esquerdo dessa equação por\(y/x\). Isso dá\(y/x=\sqrt{3}\), que pode ser reescrito como\(y=x\sqrt{3}\). Essa é a equação de uma linha reta passando pela origem com inclinação\(\sqrt{3}\). Em geral, qualquer equação polar da forma\(θ=K\) representa uma linha reta através do polo com inclinação igual\(\tan K\) a.
b. Primeiro, eleve ao quadrado os dois lados da equação. Isso faz com que\(r^2=9.\) Next seja\(r^2\) substituído por\(x^2+y^2\). Isso dá a equação\(x^2+y^2=9\), que é a equação de uma circunferência centrada na origem com raio 3. Em geral, qualquer equação polar da forma em\(r=k\) que k é uma constante positiva representa um círculo de raio k centrado na origem. (Nota: ao quadrar os dois lados de uma equação, é possível introduzir novos pontos sem querer. Isso sempre deve ser levado em consideração. No entanto, neste caso, não introduzimos novos pontos. Por exemplo,\((−3,\dfrac{π}{3})\) é o mesmo ponto que\((3,\dfrac{4π}{3})\).)
c. Multiplique os dois lados da equação por\(r\). Isso leva\(r^2=6r\cos θ−8r\sin θ\) a. Em seguida, use as fórmulas
\(r^2=x^2+y^2,x=r\cos θ,y=r\sin θ.\)
Isso dá
\(r^2=6(r\cos θ)−8(r\sin θ)\)
\(x^2+y^2=6x−8y.\)
Para colocar essa equação na forma padrão, primeiro mova as variáveis do lado direito da equação para o lado esquerdo e, em seguida, complete o quadrado.
\(x^2+y^2=6x−8y\)
\(x^2−6x+y^2+8y=0\)
\((x^2−6x)+(y^2+8y)=0\)
\((x^2−6x+9)+(y^2+8y+16)=9+16\)
\((x−3)^2+(y+4)^2=25.\)
Esta é a equação de uma circunferência com centro em\((3,−4)\) e raio 5. Observe que o círculo passa pela origem, pois o centro está a 5 unidades de distância.
Reescreva a equação\(r=\sec θ\tan θ\) em coordenadas retangulares e identifique seu gráfico.
- Dica
-
Converta em seno e cosseno e multiplique os dois lados por cosseno.
- Resposta
-
\(y=x^2\), que é a equação de uma parábola se abrindo para cima.
Agora vimos vários exemplos de desenho de gráficos de curvas definidas por equações polares. Um resumo de algumas curvas comuns é fornecido nas tabelas abaixo. Em cada equação, a e b são constantes arbitrárias.
Um cardióide é um caso especial de limaçon (pronunciado “lee-mah-son”), no qual\(a=b\) ou\(a=−b\). A rosa é uma curva muito interessante. Observe que o gráfico de\(r=3\sin 2θ\) tem quatro pétalas. No entanto, o gráfico de\(r=3\sin 3θ\) tem três pétalas, conforme mostrado.
Se o coeficiente de\(θ\) for par, o gráfico terá o dobro de pétalas do coeficiente. Se o coeficiente de\(θ\) for ímpar, o número de pétalas será igual ao coeficiente. Você é incentivado a explorar por que isso acontece. Gráficos ainda mais interessantes surgem quando o coeficiente de não\(θ\) é um número inteiro. Por exemplo, se for racional, a curva será fechada; ou seja, ela finalmente termina onde começou (Figura\(\PageIndex{8a}\)). No entanto, se o coeficiente for irracional, a curva nunca fecha (Figura\(\PageIndex{8b}\)). Embora possa parecer que a curva está fechada, um exame mais detalhado revela que as pétalas logo acima do eixo x positivo são um pouco mais grossas. Isso ocorre porque a pétala não combina perfeitamente com o ponto de partida.
Como a curva definida pelo gráfico de\(r=3\sin(πθ)\) nunca fecha, a curva mostrada na Figura\(\PageIndex{8b}\) é apenas uma representação parcial. Na verdade, esse é um exemplo de curva de preenchimento de espaço. Uma curva de preenchimento de espaço é aquela que, de fato, ocupa um subconjunto bidimensional do plano real. Nesse caso, a curva ocupa o círculo de raio 3 centrado na origem.
Lembre-se do nautilus com câmaras apresentado no prelúdio do capítulo. Essa criatura exibe uma espiral quando metade da casca externa é cortada. É possível descrever uma espiral usando coordenadas retangulares. A figura\(\PageIndex{9}\) mostra uma espiral em coordenadas retangulares. Como podemos descrever essa curva matematicamente?
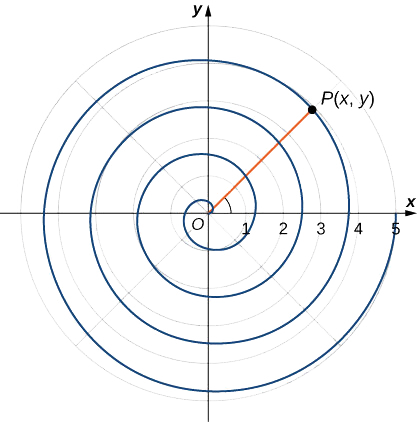
Solução
À medida que o ponto P percorre a espiral no sentido anti-horário, sua distância d da origem aumenta. Suponha que a distância d seja um múltiplo constante k do ângulo\(θ\) que o segmento de linha OP faz com o eixo x positivo. Portanto\(d(P,O)=kθ\), onde\(O\) está a origem. Agora use a fórmula da distância e um pouco de trigonometria:
\(d(P,O)=kθ\)
\(\sqrt{(x−0)^2+(y−0)^2}=k\arctan(\dfrac{y}{x})\)
\(\sqrt{x^2+y^2}=k\arctan(\dfrac{y}{x})\)
\(\arctan(\dfrac{y}{x})=\dfrac{\sqrt{x^2+y^2}}{k}\)
\(y=x\tan(\dfrac{\sqrt{x^2+y^2}}{k})\).
Embora essa equação descreva a espiral, não é possível resolvê-la diretamente para x ou y. No entanto, se usarmos coordenadas polares, a equação se torna muito mais simples. Em particular,\(d(P,O)=r\), e\(θ\) é a segunda coordenada. Portanto, a equação para a espiral se torna\(r=kθ\). Note que quando também\(θ=0\) temos\(r=0\), a espiral emana da origem. Podemos remover essa restrição adicionando uma constante à equação. Então, a equação para a espiral se torna\(r=a+kθ\) para constantes arbitrárias\(a\)\(k\) e. Isso é chamado de espiral de Arquimedes, em homenagem ao matemático grego Arquimedes.
Outro tipo de espiral é a espiral logarítmica, descrita pela função\(r=a⋅b^θ\). Um gráfico da função\(r=1.2(1.25^θ)\) é fornecido na Figura\(\PageIndex{10}\). Essa espiral descreve a forma da concha do nautilus com câmaras.
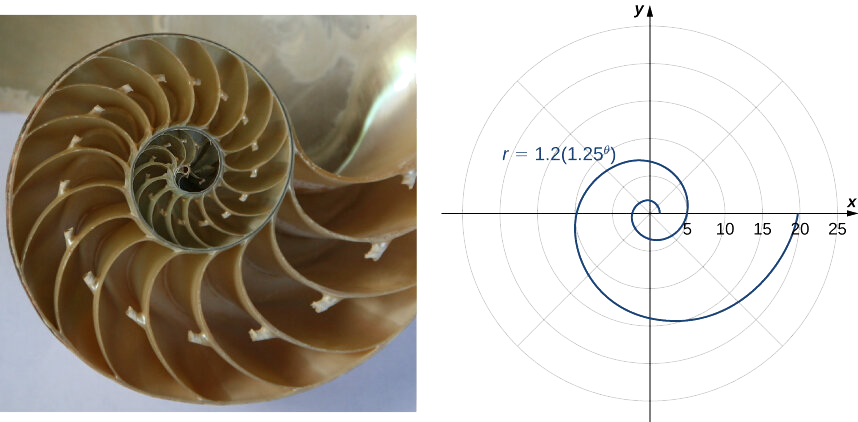
Suponha que uma curva seja descrita no sistema de coordenadas polares por meio da função\(r=f(θ)\). Uma vez que temos fórmulas de conversão de coordenadas polares para retangulares dadas por
\[x=r\cos θ \nonumber \]
\[y=r\sin θ \nonumber \],
é possível reescrever essas fórmulas usando a função
\[x=f(θ)\cos θ \nonumber \]
\[y=f(θ)\sin θ. \nonumber \]
Esta etapa fornece uma parametrização da curva em coordenadas retangulares usando\(θ\) como parâmetro. Por exemplo, a fórmula espiral\(r=a+bθ\) da Figura se torna
\[x=(a+bθ)\cos θ \nonumber \]
\[y=(a+bθ)\sin θ. \nonumber \]
Deixar\(θ\) variar de\(−∞\) a\(∞\) gera toda a espiral.
Simetria em coordenadas polares
Ao estudar simetria de funções em coordenadas retangulares (ou seja, na forma\(y=f(x)\)), falamos sobre simetria em relação ao eixo y e simetria em relação à origem. Em particular, se\(f(−x)=f(x)\) para todos\(x\) no domínio de\(f\), então\(f\) é uma função par e seu gráfico é simétrico em relação ao eixo y. Se\(f(−x)=−f(x)\) para todo x no domínio de\(f\), então f é uma função ímpar e seu gráfico é simétrico em relação à origem. Ao determinar quais tipos de simetria um gráfico exibe, podemos aprender mais sobre a forma e a aparência do gráfico. A simetria também pode revelar outras propriedades da função que gera o gráfico. A simetria nas curvas polares funciona de forma semelhante.
Considere uma curva gerada pela função\(r=f(θ)\) em coordenadas polares.
- A curva é simétrica em relação ao eixo polar se, para cada ponto\((r,θ)\) no gráfico, o ponto também\((r,−θ)\) estiver no gráfico. Da mesma forma, a equação\(r=f(θ)\) permanece inalterada ao\(θ\) substituir por\(−θ\).
- A curva é simétrica\((r,θ)\) em relação ao polo se, para cada ponto do gráfico, o ponto também\((r,π+θ)\) estiver no gráfico. Da mesma forma, a equação\(r=f(θ)\) permanece inalterada ao\(r\) substituir\(−r\) por ou\(θ\) por\(π+θ.\)
- A curva é simétrica em relação à linha vertical\(θ=\dfrac{π}{2}\) se, para cada ponto\((r,θ)\) no gráfico, o ponto também\((r,π−θ)\) estiver no gráfico. Da mesma forma, a equação\(r=f(θ)\) permanece inalterada quando\(θ\) é substituída por\(π−θ\).
A tabela a seguir mostra exemplos de cada tipo de simetria.
Encontre a simetria da rosa definida pela equação\(r=3\sin(2θ)\) e crie um gráfico.
Solução
Suponha que o ponto\((r,θ)\) esteja no gráfico de\(r=3\sin(2θ).\)
i. Para testar a simetria sobre o eixo polar, primeiro tente\(θ\) substituir por\(−θ\). Isso dá\(r=3\sin(2(−θ))=−3\sin(2θ)\). Como isso muda a equação original, esse teste não é satisfeito. No entanto, retornando à equação original e\(r\) substituindo por\(−r\) e\(θ\) por\(π−θ\) rendimentos
\[ \begin{align*} −r&=3\sin(2(π−θ)) \\[4pt] −r &=3\sin(2π−2θ) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3\sin2θ. \end{align*}\]
Multiplicando os dois lados dessa equação por\(−1\) dá\(r=3\sin 2θ\), que é a equação original. Isso demonstra que o gráfico é simétrico em relação ao eixo polar.
ii. Para testar a simetria em relação ao pólo, primeiro\(r\) substitua por\(−r\), o que produz\(−r=3\sin(2θ)\). Multiplicando os dois lados por\(−1\) dá\(r=−3\sin(2θ)\), o que não concorda com a equação original. Portanto, a equação não passa no teste dessa simetria. No entanto, retornando à equação original e\(θ\) substituindo por\(θ+π\) dá
\[ \begin{align*} r&=3\sin(2(θ+π)) \\[4pt] &=3\sin(2θ+2π) \\[4pt] &=3(\sin 2θ \cos 2π + \cos 2θ \sin 2π) \\[4pt] &=3\sin 2θ. \end{align*}\]
Como isso está de acordo com a equação original, o gráfico é simétrico em relação ao polo.
iii. Para testar a simetria em relação à linha vertical\(θ=\dfrac{π}{2}\), primeiro substitua por\(−r\) e\(θ\) por\(−θ\).\(r\)
\[ \begin{align*} −r &=3\sin(2(−θ)) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3 \sin 2θ. \end{align*}\]
Multiplicando os dois lados dessa equação por\(−1\) dá\(r=3\sin 2θ\), que é a equação original. Portanto, o gráfico é simétrico em relação à linha vertical\(θ=\dfrac{π}{2}\).
Este gráfico tem simetria em relação ao eixo polar, à origem e à linha vertical que passa pelo polo. Para representar graficamente a função, tabule os valores\(θ\) entre\(0\) e\(π/2\) e, em seguida, reflita o gráfico resultante.
| 0 | 0 |
| \(\dfrac{π}{6}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{4}\) | 3 |
| \(\dfrac{π}{3}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{2}\) | 0 |
Isso dá uma pétala da rosa, conforme mostrado no gráfico a seguir.
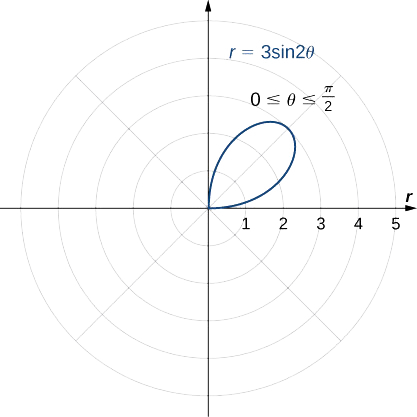
Refletindo essa imagem nos outros três quadrantes, obtém-se o gráfico inteiro conforme mostrado.
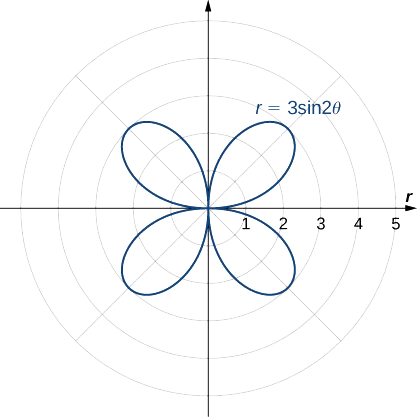
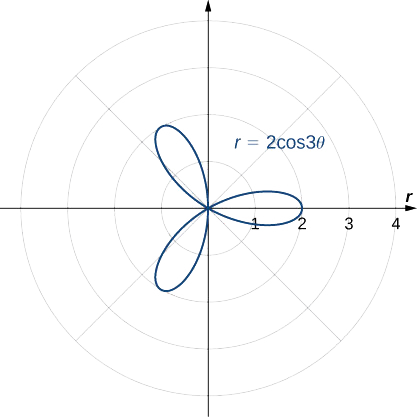
Determine a simetria do gráfico determinada pela equação\(r=2\cos(3θ)\) e crie um gráfico.
- Dica
-
Nota de uso.
- Resposta
-
Simétrico em relação ao eixo polar.
Conceitos-chave
- O sistema de coordenadas polares fornece uma forma alternativa de localizar pontos no plano.
- Converta pontos entre coordenadas retangulares e polares usando as fórmulas
\[x=r\cos θ \text{ and } y=r\sin θ \nonumber \]
e
\[r=\sqrt{x^2+y^2} \text{ and} \tan θ=\dfrac{y}{x}. \nonumber \]
- Para esboçar uma curva polar a partir de uma determinada função polar, faça uma tabela de valores e aproveite as propriedades periódicas.
- Use as fórmulas de conversão para converter equações entre coordenadas retangulares e polares.
- Identifique a simetria nas curvas polares, que pode ocorrer através do polo, do eixo horizontal ou do eixo vertical.
Glossário
- coordenada angular
- \(θ\)o ângulo formado por um segmento de linha conectando a origem a um ponto no sistema de coordenadas polares com o eixo radial (x) positivo, medido no sentido anti-horário
- cardióide
- uma curva plana traçada por um ponto no perímetro de um círculo que está rolando em torno de um círculo fixo do mesmo raio; a equação de um cardióide é\(r=a(1+\sin θ)\) ou\(r=a(1+\cos θ)\)
- limaçon
- o gráfico da equação\(r=a+b\sin θ\) ou\(r=a+b\cos θ.\) Se\(a=b\), então, o gráfico é um cardióide
- eixo polar
- o eixo horizontal no sistema de coordenadas polares correspondente a\(r≥0\)
- sistema de coordenadas polares
- um sistema para localizar pontos no avião. As coordenadas são\(r\), a coordenada radial e\(θ\), a coordenada angular
- equação polar
- uma equação ou função que relaciona a coordenada radial com a coordenada angular no sistema de coordenadas polares
- poste
- o ponto central do sistema de coordenadas polares, equivalente à origem de um sistema cartesiano
- coordenada radial
- \(r\)a coordenada no sistema de coordenadas polares que mede a distância de um ponto no plano até o polo
- rosa
- gráfico da equação polar\(r=a\cos 2θ\) ou\(r=a\sin 2θ\) para uma constante positiva\(a\)
- curva de preenchimento de espaço
- uma curva que ocupa completamente um subconjunto bidimensional do plano real


