Skip to main content
Global

10.1E: Exercícios para a Seção 10.1

  1. Last updated
  2. Save as PDF
  • Page ID
    187785

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 4, indique se cada afirmação é verdadeira ou dê um exemplo para mostrar que ela é falsa.

    1) Se\(\displaystyle \sum_{n=1}^∞a_nx^n\) convergir, então\(a_nx^n→0\) como\(n→∞.\)

    Responda
    É verdade. Se uma série converge, seus termos tendem a zero.

    2)\(\displaystyle \sum_{n=1}^∞a_nx^n\) converge em\(x=0\) para qualquer número real\(a_n\).

    3) Dada qualquer sequência\(a_n\), sempre há alguma\(R>0\), possivelmente muito pequena, que\(\displaystyle \sum_{n=1}^∞a_nx^n\) converge\((−R,R)\).

    Responda
    Falso. Isso implicaria que\(a_nx^n→0\) para\(|x|<R\). Se\(a_n=n^n\), então\(a_nx^n=(nx)^n\) não tende a zero para nenhum\(x≠0\).

    4) Se\(\displaystyle \sum_{n=1}^∞a_nx^n\) tiver raio de convergência\(R>0\) e se for\(|b_n|≤|a_n|\) para todos\(n\), então o raio de convergência de\(\displaystyle \sum_{n=1}^∞b_nx^n\) é maior ou igual\(R\) a.

    5) Suponha que\(\displaystyle \sum_{n=0}^∞a_n(x−3)^n\) converja em\(x=6\). Em qual dos seguintes pontos a série também deve convergir? Use o fato de que se\(\displaystyle \sum a_n(x−c)^n\) converge para\(x\), então ele converge em qualquer ponto mais próximo\(c\) de\(x\).

    uma.\(x=1\)

    b.\(x=2\)

    c.\(x=3\)

    d.\(x=0\)

    e.\(x=5.99\)

    f.\(x=0.000001\)

    Responda
    Deve convergir em\((0,6]\) e, portanto, em: a.\(x=1\)\(x=2\); b.\(x=3\); c.\(x=0\); d.\(x=5.99\); e.; e\(x=0.000001\) f.

    6) Suponha que\(\displaystyle \sum_{n=0}^∞a_n(x+1)^n\) converja em\(x=−2\). Em qual dos seguintes pontos a série também deve convergir? Use o fato de que se\(\displaystyle \sum a_n(x−c)^n\) converge para\(x\), então ele converge em qualquer ponto mais próximo\(c\) de\(x\).

    uma.\(x=2\)

    b.\(x=−1\)

    c.\(x=−3\)

    d.\(x=0\)

    e.\(x=0.99\)

    f.\(x=0.000001\)

    Nos exercícios a seguir, suponha que,\(\left|\dfrac{a_{n+1}}{a_n}\right|→1\) como\(n→∞.\) Encontre o raio de convergência para cada série.

    7)\(\displaystyle \sum_{n=0}^∞a_n2^nx^n\)

    Responda
    \(\left|\dfrac{a_{n+1}2^{n+1}x^{n+1}}{a_n2^nx^n}\right| =2|x|\left|\dfrac{a_{n+1}}{a_n}\right|→2|x|\)então\(R=\frac{1}{2}\)

    8)\(\displaystyle \sum_{n=0}^∞\frac{a_nx^n}{2^n}\)

    9)\(\displaystyle \sum_{n=0}^∞\frac{a_nπ^nx^n}{e^n}\)

    Responda
    \(\left|\dfrac{a_{n+1}(\dfrac{π}{e})^{n+1}x^{n+1}}{a_n(\dfrac{π}{e})^nx^n}\right| =\dfrac{π|x|}{e}\left|\dfrac{a_{n+1}}{a_n}\right|→\dfrac{π|x|}{e}\)então\(R=\frac{e}{π}\)

    10)\(\displaystyle \sum_{n=0}^∞\frac{a_n(−1)^nx^n}{10^n}\)

    11)\(\displaystyle \sum_{n=0}^∞a_n(−1)^nx^{2n}\)

    Responda
    \(\left|\dfrac{a_{n+1}(−1)^{n+1}x^{2n+2}}{a_n(−1)^nx^{2n}}\right| =|x^2|\left|\dfrac{a_{n+1}}{a_n}\right|→|x^2|\)então\(R=1\)

    12)\(\displaystyle \sum_{n=0}^∞a_n(−4)^nx^{2n}\)

    Nos exercícios 13 a 22, determine o raio de convergência\(R\) e o intervalo de convergência para\(\displaystyle \sum a_nx^n\) com os coeficientes dados\(a_n\).

    13)\(\displaystyle \sum_{n=1}^∞\frac{(2x)^n}{n}\)

    Responda
    \(a_n=\dfrac{2^n}{n}\)\(\dfrac{a_{n+1}x}{a_n}→2x\)então. então\(R=\frac{1}{2}\). Quando\(x=\frac{1}{2}\) a série é harmônica e diverge. Quando\(x=−\frac{1}{2}\) a série está alternando harmônica e converge. O intervalo de convergência é\(I=\big[−\frac{1}{2},\frac{1}{2}\big)\).

    14)\(\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\sqrt{n}}\)

    15)\(\displaystyle \sum_{n=1}^∞\frac{nx^n}{2^n}\)

    Responda
    \(a_n=\dfrac{n}{2^n}\)\(\dfrac{a_{n+1}x}{a_n}→\dfrac{x}{2}\)então\(R=2\). Quando\(x=±2\) a série diverge pelo teste de divergência. O intervalo de convergência é\(I=(−2,2)\).

    16)\(\displaystyle \sum_{n=1}^∞\frac{nx^n}{e^n}\)

    17)\(\displaystyle \sum_{n=1}^∞\frac{n^2x^n}{2^n}\)

    Responda
    \(a_n=\dfrac{n^2}{2^n}\)então\(R=2\). Quando\(x=±2\) a série diverge pelo teste de divergência. O intervalo de convergência é\(I=(−2,2).\)

    18)\(\displaystyle \sum_{k=1}^∞\frac{k^ex^k}{e^k}\)

    19)\(\displaystyle \sum_{k=1}^∞\frac{π^kx^k}{k^π}\)

    Responda
    \(a_k=\dfrac{π^k}{k^π}\)então\(R=\frac{1}{π}\). Quando\(x=±\frac{1}{π}\) a série é uma\(p\) série absolutamente convergente. O intervalo de convergência é\(I=\left[−\frac{1}{π},\frac{1}{π}\right].\)

    20)\(\displaystyle \sum_{n=1}^∞\frac{x^n}{n!}\)

    21)\(\displaystyle \sum_{n=1}^∞\frac{10^nx^n}{n!}\)

    Responda
    \(a_n=\dfrac{10^n}{n!},\dfrac{a_{n+1}x}{a_n}=\dfrac{10x}{n+1}→0<1\)então a série converge para todos\(x\) pelo teste de proporção\(I=(−∞,∞)\) e.

    22)\(\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\ln(2n)}\)

    Nos exercícios 23 a 28, determine o raio de convergência de cada série.

    23)\(\displaystyle \sum_{k=1}^∞\frac{(k!)^2x^k}{(2k)!}\)

    Responda
    \(a_k=\dfrac{(k!)^2}{(2k)!}\)\(\dfrac{a_{k+1}}{a_k}=\dfrac{(k+1)^2}{(2k+2)(2k+1)}→\dfrac{1}{4}\)então\(R=4\)

    24)\(\displaystyle \sum_{n=1}^∞\frac{(2n)!x^n}{n^{2n}}\)

    25)\(\displaystyle \sum_{k=1}^∞\frac{k!}{1⋅3⋅5⋯(2k−1)}x^k\)

    Responda
    \(a_k=\dfrac{k!}{1⋅3⋅5⋯(2k−1)}\)\(\dfrac{a_{k+1}}{a_k}=\dfrac{k+1}{2k+1}→\dfrac{1}{2}\)então\(R=2\)

    26)\(\displaystyle \sum_{k=1}^∞\frac{2⋅4⋅6⋯2k}{(2k)!}x^k\)

    27)\(\displaystyle \sum_{n=1}^∞\frac{x^n}{(^{2n}_n)}\) onde\((^n_k)=\dfrac{n!}{k!(n−k)!}\)

    Responda
    \(a_n=\dfrac{1}{(^{2n}_n)}\)\(\dfrac{a_{n+1}}{a_n}=\dfrac{\big((n+1)!\big)^2}{(2n+2)!}\dfrac{2n!}{(n!)^2}=\dfrac{(n+1)^2}{(2n+2)(2n+1)}→\dfrac{1}{4}\)então\(R=4\)

    28)\(\displaystyle \sum_{n=1}^∞\sin^2nx^n\)

    Nos exercícios 29 a 32, use o teste de proporção para determinar o raio de convergência de cada série.

    29)\(\displaystyle \sum_{n=1}^∞\frac{(n!)^3}{(3n)!}x^n\)

    Responda
    \(\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)^3}{(3n+3)(3n+2)(3n+1)}→\dfrac{1}{27}\)então\(R=27\)

    30)\(\displaystyle \sum_{n=1}^∞\frac{2^{3n}(n!)^3}{(3n)!}x^n\)

    31)\(\displaystyle \sum_{n=1}^∞\frac{n!}{n^n}x^n\)

    Responda
    \(a_n=\dfrac{n!}{n^n}\)\(\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)!}{n!}\dfrac{n^n}{(n+1)^{n+1}}=(\dfrac{n}{n+1})^n→\dfrac{1}{e}\)então\(R=e\)

    32)\(\displaystyle \sum_{n=1}^∞\frac{(2n)!}{n^{2n}}x^n\)

    Nos exercícios a seguir, considerando que\(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\) com a convergência em\((−1,1)\), encontre a série de potências para cada função com o centro dado\(a,\) e identifique seu intervalo de convergência.

    33)\(f(x)=\dfrac{1}{x};a=1\) (Dica:\(\dfrac{1}{x}=\dfrac{1}{1−(1−x)})\)

    Responda
    \(\displaystyle f(x)=\sum_{n=0}^∞(1−x)^n\)em\(I=(0,2)\)

    34)\(f(x)=\dfrac{1}{1−x^2};a=0\)

    35)\(f(x)=\dfrac{x}{1−x^2};a=0\)

    Responda
    \(\displaystyle \sum_{n=0}^∞x^{2n+1}\)em\(I=(−1,1)\)

    36)\(f(x)=\dfrac{1}{1+x^2};a=0\)

    37)\(f(x)=\dfrac{x^2}{1+x^2};a=0\)

    Responda
    \(\displaystyle \sum_{n=0}^∞(−1)^nx^{2n+2}\)em\(I=(−1,1)\)

    38)\(f(x)=\dfrac{1}{2−x};a=1\)

    39)\(f(x)=\dfrac{1}{1−2x};a=0.\)

    Responda
    \(\displaystyle \sum_{n=0}^∞2^nx^n\)em\(\left(−\frac{1}{2},\frac{1}{2}\right)\)

    40)\(f(x)=\dfrac{1}{1−4x^2};a=0\)

    41)\(f(x)=\dfrac{x^2}{1−4x^2};a=0\)

    Responda
    \(\displaystyle \sum_{n=0}^∞4^nx^{2n+2}\)em\(\left(−\frac{1}{2},\frac{1}{2}\right)\)

    42)\(f(x)=\dfrac{x^2}{5−4x+x^2};a=2\)

    Use o resultado do exercício 43 para encontrar o raio de convergência da série dada nos exercícios subsequentes (44 - 47).

    43) Explique por que, se\(|a_n|^{1/n}→r>0,\) então,\(|a_nx^n|^{1/n}→|x|r<1\) quando\(|x|<\frac{1}{r}\) e, portanto, o raio de convergência de\(\displaystyle \sum_{n=1}^∞a_nx^n\) é\(R=\frac{1}{r}\).

    Responda
    \(|a_nx^n|^{1/n}=|a_n|^{1/n}|x|→|x|r\)como\(n→∞\) e\(|x|r<1\) quando\(|x|<\frac{1}{r}\). Portanto,\(\displaystyle \sum_{n=1}^∞a_nx^n\) converge quando\(|x|<\frac{1}{r}\) pelo teste\(n^{\text{th}}\) raiz.

    44)\(\displaystyle \sum_{n=1}^∞\frac{x^n}{n^n}\)

    45)\(\displaystyle \sum_{k=1}^∞\left(\frac{k−1}{2k+3}\right)^kx^k\)

    Responda
    \(a_k=\left(\dfrac{k−1}{2k+3}\right)^k\)\((a_k)^{1/k}→\frac{1}{2}<1\)então\(R=2\)

    46)\(\displaystyle \sum_{k=1}^∞(\frac{2k^2−1}{k^2+3})^kx^k\)

    47)\(\displaystyle \sum_{n=1}^∞a_n=(n^{1/n}−1)^nx^n\)

    Responda
    \(a_n=(n^{1/n}−1)^n\)\((a_n)^{1/n}→0\)então\(R=∞\)

    48) Suponha que\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\)\(a_n=0\)\(n\) seja igual. Explique por quê\(p(x)=p(−x).\)

    49) Suponha que\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\)\(a_n=0\)\(n\) seja estranho. Explique por quê\(p(x)=−p(−x).\)

    Responda
    Podemos reescrever\(\displaystyle p(x)=\sum_{n=0}^∞a_{2n+1}x^{2n+1}\) e\(p(x)=p(−x)\) desde então\(x^{2n+1}=−(−x)^{2n+1}\).

    50) Suponha que isso\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) converja em\((−1,1]\). Encontre o intervalo de convergência de\(p(Ax)\).

    51) Suponha que isso\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) converja em\((−1,1]\). Encontre o intervalo de convergência de\(p(2x−1)\).

    Responda
    Se\(y=2x−1∈[−1,1]\) assim\(x∈[0,1],\) for,\(\displaystyle p(2x−1)=p(y)=\sum_{n=0}^∞a_ny^n\) converge.

    Nos exercícios a seguir, suponha que isso\(\displaystyle p(x)=\sum_{n=0}^∞a_nx^n\) satisfaça\(\displaystyle \lim_{n→∞}\frac{a_{n+1}}{a_n}=1\) onde\(a_n≥0\) para cada um\(n\). Indique se cada série converge no intervalo\((−1,1)\) completo ou se não há informações suficientes para tirar uma conclusão. Use o teste de comparação quando apropriado.

    52)\(\displaystyle \sum_{n=0}^∞a_nx^{2n}\)

    53)\(\displaystyle \sum_{n=0}^∞a_{2n}x^{2n}\)

    Responda
    Converge\((−1,1)\) pelo teste de proporção

    54)\(\displaystyle \sum_{n=0}^∞a_{2n}x^n\) (Dica:\(x=±\sqrt{x^2}\))

    55)\(\displaystyle \sum_{n=0}^∞a_{n^2}x^{n^2}\) (Dica: deixe\(b_k=a_k\)\(k=n^2\) para alguns\(n\), caso contrário\(b_k=0\).)

    Responda
    Considere a série\(\displaystyle \sum b_kx^k\) onde,\(b_k=a_k\) se\(k=n^2\) e\(b_k=0\) não. Então,\(b_k≤a_k\) e assim, a série converge\((−1,1)\) pelo teste de comparação.

    56) Suponha que\(p(x)\) seja um polinômio de grau\(N\). Encontre o raio e o intervalo de convergência de\(\displaystyle \sum_{n=1}^∞p(n)x^n\).

    57) [T] Faça um gráfico dos gráficos de\(\dfrac{1}{1−x}\) e das somas parciais\(\displaystyle S_N=\sum_{n=0}^Nx^n\) de\(n=10,20,30\) no intervalo\([−0.99,0.99]\). Comente sobre a aproximação de\(\dfrac{1}{1−x}\) por\(S_N\) perto\(x=−1\) e por perto\(x=1\) à medida que\(N\) aumenta.

    Responda

    A aproximação é mais precisa de perto\(x=−1\). As somas parciais acompanham\(\dfrac{1}{1−x}\) mais de perto os\(N\) aumentos, mas nunca são precisas,\(x=1\) pois a série diverge lá.

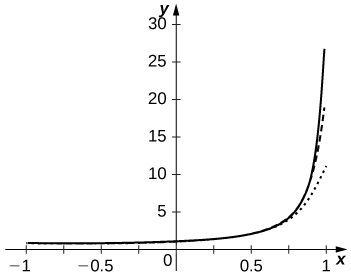
    Esta figura é o gráfico de y = 1/ (1-x), que é uma curva crescente com assíntota vertical em 1.

    58) [T] Faça um gráfico dos gráficos de\(−\ln(1−x)\) e das somas parciais\(\displaystyle S_N=\sum_{n=1}^N\frac{x^n}{n}\) de\(n=10,50,100\) no intervalo\([−0.99,0.99]\). Comente sobre o comportamento das somas próximas\(x=−1\) e próximas\(x=1\) à medida que\(N\) aumenta.

    59) [T] Faça um gráfico das somas parciais\(\displaystyle S_n=\sum_{n=1}^N\frac{x^n}{n^2}\) de\(n=10,50,100\) no intervalo\([−0.99,0.99]\). Comente sobre o comportamento das somas próximas\(x=−1\) e próximas\(x=1\) à medida que\(N\) aumenta.

    Responda

    A aproximação parece se estabilizar rapidamente perto de ambos\(x=±1\).

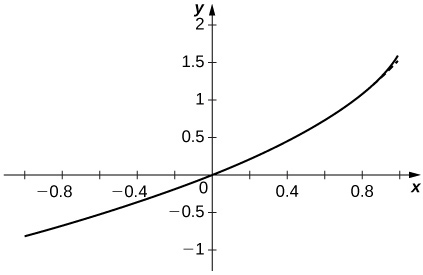
    Esta figura é o gráfico de y = -ln (1-x), que é uma curva crescente passando pela origem.

    60) [T] Faça um gráfico das somas parciais\(\displaystyle S_N=\sum_{n=1}^N(\sin n) x^n\) de\(n=10,50,100\) no intervalo\([−0.99,0.99]\). Comente sobre o comportamento das somas próximas\(x=−1\) e próximas\(x=1\) à medida que\(N\) aumenta.

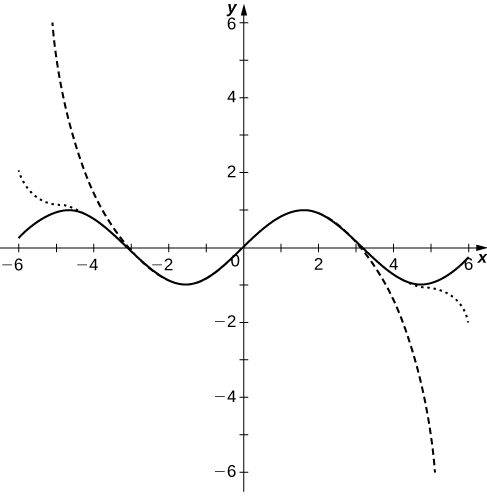
    61) [T] Faça um gráfico das somas parciais\(\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n+1}}{(2n+1)!}\) de\(n=3,5,10\) no intervalo\([−2π,2π]\). Comente sobre como esses gráficos se aproximam com\(\sin x\) os\(N\) aumentos.

    Responda

    As curvas polinomiais têm raízes próximas às de\(\sin x\) até seu grau e, em seguida, os polinômios divergem de\(\sin x\).

    Esta figura é o gráfico das somas parciais de (-1) ^n vezes x^ (2n+1) dividida por (2n+1)! Para n=3,5,10. As curvas se aproximam da curva senoidal próxima à origem e depois se separam à medida que as curvas se afastam da origem.

    62) [T] Faça um gráfico das somas parciais\(\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n}}{(2n)!}\) de\(n=3,5,10\) no intervalo\([−2π,2π]\). Comente sobre como esses gráficos se aproximam com\(\cos x\) os\(N\) aumentos.