10.1: Séries e funções de potência

Last updated
Save as PDF

Page ID: 187776

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Identifique uma série de potências e forneça exemplos delas.
Determine o raio de convergência e o intervalo de convergência de uma série de potências.
Use uma série de potências para representar uma função.

Uma série de potência é um tipo de série com termos que envolvem uma variável. Mais especificamente, se a variável for$x$, todos os termos da série envolvem potências de$x$. Como resultado, uma série de potências pode ser considerada um polinômio infinito. As séries Power são usadas para representar funções comuns e também para definir novas funções. Nesta seção, definimos séries de potência e mostramos como determinar quando uma série de potência converge e quando ela diverge. Também mostramos como representar determinadas funções usando séries de potência.

Forma de uma série Power

Uma série do formulário

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots , \nonumber \]

onde$x$ é uma variável e os coeficientes$c_n$ são constantes, é conhecida como série de potências. A série

\[1+x+x^2+\ldots =\sum_{n=0}^∞x^n \nonumber \]

é um exemplo de uma série de potências. Como essa série é uma série geométrica com proporção$r=|x|$, sabemos que ela converge se$|x|<1$ e diverge se$|x|≥1.$

Definição$\PageIndex{1}$: Power Series

Uma série do formulário

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots \nonumber \]

é uma série de potências$x=0.$ centrada na série A da forma

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

é uma série de potências centrada em$x=a$.

Para tornar essa definição precisa, estipulamos isso$x^0=1$ e$(x−a)^0=1$ até mesmo quando$x=0$ e$x=a$, respectivamente.

A série

\[\sum_{n=0}^∞\dfrac{x^n}{n!}=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots \nonumber \]

\[\sum_{n=0}^∞n!x^n=1+x+2!x^2+3!x^3+\ldots \nonumber \]

são ambas séries de potência centradas$x=0.$ na série

\[\sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}=1+\dfrac{x−2}{2⋅3}+\dfrac{(x−2)^2}{3⋅3^2}+\dfrac{(x−2)^3}{4⋅3^3}+\ldots \nonumber \]

é uma série de potências centrada em$x=2$.

Convergência de uma série de potências

Como os termos em uma série de potências envolvem uma variável$x$, a série pode convergir para certos valores de$x$ e divergir para outros valores de$x$. Para uma série de potência centrada em$x=a$, o valor da série em$x=a$ é dado por$c_0$. Portanto, uma série de potências sempre converge em seu centro. Algumas séries de potência convergem apenas nesse valor de$x$. A maioria das séries de potência, no entanto, converge para mais de um valor de$x$. Nesse caso, a série de potências converge para todos os números reais$x$ ou converge para todos$x$ em um intervalo finito. Por exemplo, a série geométrica$\displaystyle \sum_{n=0}^∞x^n$ converge para todos$x$ no intervalo$(−1,1)$, mas diverge para todos$x$ fora desse intervalo. Agora resumimos essas três possibilidades para uma série de potência geral.

Nota$\PageIndex{1}$: Convergence of a Power Series

Considere a série de potência$\displaystyle \sum_{n=0}^∞c_n(x−a)^n.$ A série satisfaz exatamente uma das seguintes propriedades:

A série converge$x=a$ e diverge para todos$x≠a.$
A série converge para todos os números reais$x$.
Existe um número real$R>0$ tal que a série converge se$|x−a|<R$ e diverge se$|x−a|>R$. Nos valores em$x$ que |x−a|=R, a série pode convergir ou divergir.

Prova

Suponha que a série de potência esteja centrada em$a=0$. (Para uma série centrada em um valor diferente de zero, o resultado segue deixando$y=x−a$ e considerando a série

\[ \sum_{n=1}^∞c_ny^n. \nonumber \]

Devemos primeiro provar o seguinte fato:

Se existe um número$d≠0$ real que$\displaystyle \sum_{n=0}^∞c_nd^n$ converja, então a série$\displaystyle \sum_{n=0}^∞c_nx^n$ converge absolutamente para tudo$x$ isso$|x|<|d|.$

Uma vez que$\displaystyle \sum_{n=0}^∞c_nd^n$ converge, o enésimo termo$c_nd^n→0$ foi$n→∞$. Portanto, existe um número inteiro$N$ tal que$|c_nd^n|≤1$ para toda$n≥N.$ escrita

\[|c_nx^n|=|c_nd^n| \left|\dfrac{x}{d}\right|^n, \nonumber \]

concluímos que, para todo o N≥n,

\[|c_nx^n|≤\left|\dfrac{x}{d}\right|^n. \nonumber \]

A série

\[\sum_{n=N}^∞\left|\dfrac{x}{d}\right|^n \nonumber \]

é uma série geométrica que converge se$|\dfrac{x}{d}|<1.$ Portanto, pelo teste de comparação, concluímos que$\displaystyle \sum_{n=N}^∞c_nx^n$ também converge para$|x|<|d|$. Como podemos adicionar um número finito de termos a uma série convergente, concluímos que$\displaystyle \sum_{n=0}^∞c_nx^n$ converge para$|x|<|d|.$

Com esse resultado, agora podemos provar o teorema. Considere a série

\[\sum_{n=0}^∞a_nx^n \nonumber \]

e$S$ seja o conjunto de números reais para os quais a série converge. Suponha que o conjunto$S={0}.$ Então a série se enquadre no caso i.

Suponha que o conjunto$S$ seja o conjunto de todos os números reais. Então, a série se enquadra no caso ii. Suponha que$S≠{0}$ e não$S$ seja o conjunto de números reais. Então, existe um número real de$x*≠0$ tal forma que a série não converge. Assim, a série não pode convergir para nada$x$ disso$|x|>|x*|$. Portanto, o conjunto$S$ deve ser um conjunto limitado, o que significa que ele deve ter o menor limite superior. (Esse fato decorre da propriedade Least Upper Bound para os números reais, que está além do escopo deste texto e é abordada em cursos de análise real.) Chame esse menor limite superior$R$. Desde então$S≠{0}$, o número$R>0$. Portanto, a série converge para tudo$x$ isso$|x|<R,$ e a série se enquadra no caso iii.

□

Se uma série se$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ enquadra no caso iii. de Note, então a série converge$|x−a|<R$ para tudo$x$ isso que para alguns$R>0$ e diverge para tudo$x$ isso$|x−a|>R$. A série pode convergir ou divergir nos valores em$x$ que$|x−a|=R$. O conjunto de valores$x$ para o qual a série$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ converge é conhecido como intervalo de convergência. Como a série diverge para todos os valores$x$ em que$|x−a|>R$, o comprimento do intervalo é e$2R$, portanto, o raio do intervalo é$R$. O valor$R$ é chamado de raio de convergência. Por exemplo, como a série$\displaystyle \sum_{n=0}^∞x^n$ converge para todos os valores$x$ no intervalo$(−1,1)$ e diverge para todos os valores, de$x$ forma que$|x|≥1$, o intervalo de convergência dessa série é$(−1,1)$. Como o comprimento do intervalo é$2$, o raio de convergência é$1$.

Definição: raio de convergência

Considere a série de potências$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$. O conjunto de números reais$x$ em que a série converge é o intervalo de convergência. Se existe um número real$R>0$ tal que a série converge$|x−a|<R$ e diverge$|x−a|>R,$, então$R$ é o raio de convergência. Se a série convergir apenas em$x=a$, dizemos que o raio de convergência é$R=0$. Se a série convergir para todos os números reais$x$, dizemos que o raio de convergência é$R=∞$ (Figura$\PageIndex{1}$).

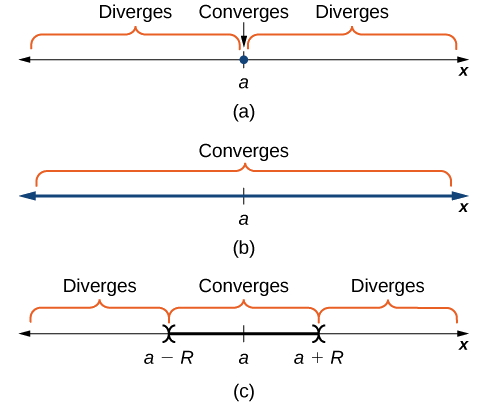
Essa figura tem três linhas numéricas, cada uma rotulada com x. No meio de cada reta numérica há um ponto chamado a. A primeira linha numérica “diverge” sobre toda a linha à esquerda de a e “diverge” sobre a linha à direita de a. No próprio ponto a, ela é rotulada como “converge”. A segunda linha numérica tem “convergências” rotuladas para toda a linha. A terceira reta numérica tem pontos rotulados em A-r, a e a+r. À esquerda de A-r, a reta numérica é rotulada como “diverge”. Entre a-R e a+R, a reta numérica é rotulada como “converge” e à direita de a+R a reta numérica é rotulada como “diverge”. — Figura$\PageIndex{1}$: Para um$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ gráfico em série (a) mostra um raio de convergência em$R=0$, o gráfico (b) mostra um raio de convergência em$R=∞$ e o gráfico (c) mostra um raio de convergência em$R$. Para o gráfico (c), notamos que a série pode ou não convergir nos pontos finais$x=a+R$$x=a−R$ e.

Para determinar o intervalo de convergência para uma série de potências, normalmente aplicamos o teste de razão. No exemplo$\PageIndex{1}$, mostramos as três possibilidades diferentes ilustradas na Figura$\PageIndex{1}$.

Exemplo$\PageIndex{1}$: Finding the Interval and Radius of Convergence

Para cada uma das séries a seguir, encontre o intervalo e o raio de convergência.

$\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}$
$\displaystyle \sum_{n=0}^∞n!x^n$
$\displaystyle \sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}$

Solução

a. Para verificar a convergência, aplique o teste de proporção. Nós temos

\ [\ begin {align*} ρ &=\ lim_ {n→∞}\ esquerda|\ dfrac {\ dfrac {x^ {n+1}} {(n+1)!}} {\ dfrac {x^n} {n!}} \ right|\\ [4pt]
&=\ lim_ {n→∞}\ esquerda|\ dfrac {x^ {n+1}} {(n+1)!} ==\ dfrac {n!} {x^n}\ direita|\\ [4pt]
&=\ lim_ {n→∞}\ esquerda|\ dfrac {x^ {n+1}} {(n+1) ρ n!} ==\ dfrac {n!} {x^n}\ direita|\\ [4pt]
&=\ lim_ {n→∞}\ esquerda|\ dfrac {x} {n+1}\ direita|\\ [4pt]
&=|x|\ lim_ {n→∞}\ dfrac {1} {n+1}\\ [4pt]
&=0<1\ end {align*}\]

para todos os valores de$x$. Portanto, a série converge para todos os números reais$x$. O intervalo de convergência é$(−∞,∞)$ e o raio de convergência é$R=∞.$

b. Aplique o teste de proporção. $x≠0$Pois, vemos que

\ [\ begin {align*} ρ &=\ lim_ {n→∞}\ left|\ dfrac {(n+1)! x^ {n+1}} {n! x^n}\ right|\\ [4pt]
&=\ lim_ {n→∞} | (n+1) x|\\ [4pt]
&=|x|\ lim_ {n→∞} (n+1)\\ [4pt]
&=∞. \ end {align*}\]

Portanto, a série diverge para todos$x≠0$. Como a série está centrada em$x=0$, ela deve convergir para lá, então a série converge apenas para$x≠0$. O intervalo de convergência é o valor único$x=0$ e o raio de convergência é$R=0$.

c. Para aplicar o teste de proporção, considere

\ [\ begin {align*} ρ &=\ lim_ {n→∞}\ esquerda|\ dfrac {\ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}} {\ dfrac {(x−2) ^n} {(n+1) 3^n}}\ direita|\\ [4pt]
&=\ lim_ {n→∞}\ esquerda|\ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}} □\ dfrac {(n+1) 3^n} {(x−2) ^n}\ direita|\\ [4pt]
&=\ lim_ {n→∞}\ esquerda|\ dfrac {(x−−2) (n+1)} {3 (n+2)}\ direito|\\ [4 pt]
&=\ dfrac {|x−2|} {3}. \ end {align*}\]

A proporção$ρ<1$ de$|x−2|<3$. Uma vez que$|x−2|<3$ implica que$−3<x−2<3,$ a série converge absolutamente se$−1<x<5$. A proporção$ρ>1$ de$|x−2|>3$. Portanto, a série diverge se$x<−1$ ou$x>5$. O teste de proporção é inconclusivo se$ρ=1$. A proporção$ρ=1$ se e somente se$x=−1$ ou$x=5$. Precisamos testar esses valores$x$ separadamente. Pois$x=−1$, a série é dada por

\[ \sum_{n=0}^∞\dfrac{(−1)^n}{n+1}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots . \nonumber \]

Como essa é a série harmônica alternada, ela converge. Assim, a série converge em$x=−1$. Pois$x=5$, a série é dada por

\[ \sum_{n=0}^∞\dfrac{1}{n+1}=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\ldots . \nonumber \]

Essa é a série harmônica, que é divergente. Portanto, a série de potência diverge em$x=5$. Concluímos que o intervalo de convergência é$[−1,5)$ e o raio de convergência é$R=3$.

Exercício$\PageIndex{1}$

Encontre o intervalo e o raio de convergência para a série

\[ \sum_{n=1}^∞\dfrac{x^n}{\sqrt{n}}. \nonumber \]

Dica: Aplique o teste de proporção para verificar a convergência absoluta.

Responda: O intervalo de convergência é$[−1,1).$ O raio de convergência é$R=1.$

Representando funções como séries de potência

Ser capaz de representar uma função por meio de um “polinômio infinito” é uma ferramenta poderosa. As funções polinomiais são as funções mais fáceis de analisar, pois envolvem apenas as operações aritméticas básicas de adição, subtração, multiplicação e divisão. Se pudermos representar uma função complicada por meio de um polinômio infinito, podemos usar a representação polinomial para diferenciá-la ou integrá-la. Além disso, podemos usar uma versão truncada da expressão polinomial para aproximar os valores da função. Então, a questão é: quando podemos representar uma função por uma série de potências?

Considere novamente a série geométrica

\[1+x+x^2+x^3+\ldots =\sum_{n=0}^∞x^n. \nonumber \]

Lembre-se de que a série geométrica

\[a+ar+ar^2+ar^3+\ldots \nonumber \]

converge se e somente se$|r|<1.$ Nesse caso, ele convergir para$\dfrac{a}{1−r}$. Portanto$|x|<1$, se a série em Example$\PageIndex{1}$ converge para$\dfrac{1}{1−x}$ e escrevemos

\[1+x+x^2+x^3+\ldots =\dfrac{1}{1−x} for|x|<1. \nonumber \]

Como resultado, somos capazes de representar a função$f(x)=\dfrac{1}{1−x}$ pela série de potências

\[1+x+x^2+x^3+\ldots when|x|<1. \nonumber \]

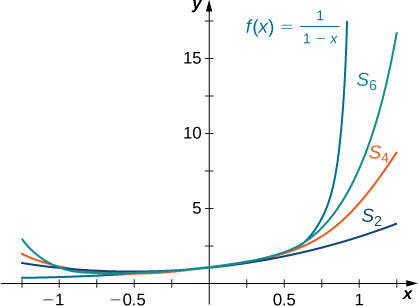
Agora mostramos graficamente como essa série fornece uma representação para a função$f(x)=\dfrac{1}{1−x}$ comparando o gráfico de$f$ com os gráficos de várias somas parciais dessa série infinita.

Exemplo$\PageIndex{2}$: Graphing a Function and Partial Sums of its Power Series

Esboce um gráfico$f(x)=\dfrac{1}{1−x}$ e os gráficos das somas$ \displaystyle S_N(x)=\sum_{n=0}^Nx^n$ parciais correspondentes$N=2,4,6$ no intervalo$(−1,1)$. Comente sobre a aproximação à$S_N$ medida que$N$ aumenta.

Solução

No gráfico da Figura, você vê que, à medida que$N$ aumenta,$S_N$ se torna uma melhor aproximação$f(x)=\dfrac{1}{1−x}$ para$x$ no intervalo$(−1,1)$.

Esta figura é o gráfico de y = 1/ (1-x), que é uma curva crescente com assíntota vertical em 1. Também neste gráfico estão três somas parciais da função, S sub 6, S sub 4 e S sub 2. Essas curvas, em ordem, gradualmente se tornam mais planas. — Figura$\PageIndex{2}$: O gráfico mostra uma função e três aproximações dela por somas parciais de uma série de potências.

Exercício$\PageIndex{2}$

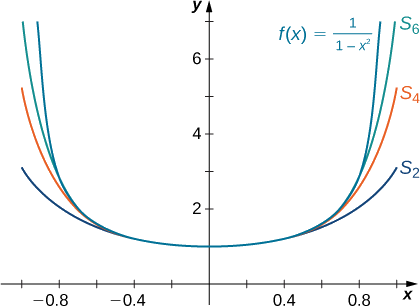
Esboce um gráfico$f(x)=\dfrac{1}{1−x^2}$ e as somas parciais correspondentes$\displaystyle S_N(x)=\sum_{n=0}^Nx^{2n}$ de$N=2,4,6$ no intervalo$(−1,1).$

Dica: $S_N(x)=1+x^2+\ldots +x^{2N}=\dfrac{1−x^{2(N+1)}}{1−x^2}$

Responda: $Esta figura é o gráfico de y = 1/ (1-x^2), que é uma curva côncava para cima, simétrica em relação ao eixo y. Também neste gráfico estão três somas parciais da função, S sub 6, S sub 4 e S sub 2. Essas curvas, em ordem, gradualmente se tornam mais planas.$

Em seguida, consideramos funções que envolvem uma expressão semelhante à soma de uma série geométrica e mostramos como representar essas funções usando séries de potências.

Exemplo$\PageIndex{3}$: Representing a Function with a Power Series

Use uma série de potências para representar cada uma das seguintes funções$f$. Encontre o intervalo de convergência.

$f(x)=\dfrac{1}{1+x^3}$
$f(x)=\dfrac{x^2}{4−x^2}$

Solução

a. Você deve reconhecer essa função$f$ como a soma de uma série geométrica, porque

\[ \dfrac{1}{1+x^3}=\dfrac{1}{1−(−x^3)}. \nonumber \]

Usando o fato de que, for$|r|<1,\dfrac{a}{1−r}$ é a soma da série geométrica

\[ \sum_{n=0}^∞ar^n=a+ar+ar^2+\ldots , \nonumber \]

vemos que, por$|−x^3|<1,$

\[ \begin{align*} \dfrac{1}{1+x^3} =\dfrac{1}{1−(−x^3)} \\[4pt] =\sum_{n=0}^∞(−x^3)^n \\[4pt] =1−x^3+x^6−x^9+\ldots . \end{align*}\]

Como essa série converge se e somente se$|−x^3|<1$, o intervalo de convergência é$(−1,1)$, e temos

\[ \dfrac{1}{1+x^3}=1−x^3+x^6−x^9+\ldots for|x|<1.\nonumber \]

b. Essa função não está na forma exata da soma de uma série geométrica. No entanto, com um pouco de manipulação algébrica, podemos relacionar f a uma série geométrica. Ao fatorar 4 dos dois termos no denominador, obtemos

\[ \begin{align*} \dfrac{x^2}{4−x^2} =\dfrac{x^2}{4(\dfrac{1−x^2}{4})}\\[4pt] =\dfrac{x^2}{4(1−(\dfrac{x}{2})^2)}.\end{align*}\]

Portanto, temos

\ [\ begin {align*}\ dfrac {x^2} {4−x^2} &=\ dfrac {x^2} {4 (1− (\ dfrac {x} {2}) ^2)}\\ [4pt]
&=\ dfrac {\ dfrac {x^2} {4}} {1− (\ dfrac {x} {2}}) ^2}\\ [4pt]
&=\ sum_ {n=0} ^∞\ dfrac {x^2} {4} (\ dfrac {x} {2}) ^ {2n}. \ end {align*}\]

A série converge desde que$|(\dfrac{x}{2})^2|<1$ (observe que quando$|(\dfrac{x}{2})^2|=1$ a série não converge). Resolvendo essa desigualdade, concluímos que o intervalo de convergência é$(−2,2)$ e

\ [\ begin {align*}\ dfrac {x^2} {4−x^2} &=\ sum_ {n=0} ^∞\ dfrac {x^ {2n+2}} {4^ {n+1}}\ [4pt]
&=\ dfrac {x^2} {4} +\ dfrac {x^4} {4^2}\ dfrac {x^6} {4^3} +\ ldots\ end {align*}\]

para$|x|<2.$

Exercício$\PageIndex{3}$

Represente a função$f(x)=\dfrac{x^3}{2−x}$ usando uma série de potências e encontre o intervalo de convergência.

Dica: Reescreva f no formulário$f(x)=\dfrac{g(x)}{1−h(x)}$ para algumas funções$g$$h$ e.

Responda: $\displaystyle \sum_{n=0}^∞\dfrac{x^{n+3}}{2^{n+1}}$com intervalo de convergência$(−2,2)$

Nas seções restantes deste capítulo, mostraremos maneiras de derivar representações de séries de potência para muitas outras funções e como podemos fazer uso dessas representações para avaliar, diferenciar e integrar várias funções.

Conceitos-chave

Para uma série de potência centrada em$x=a$, uma das três propriedades a seguir é válida:
- i. A série de potência converge apenas em$x=a$. Nesse caso, dizemos que o raio de convergência é$R=0$.
- ii. A série power converge para todos os números reais$x$. Nesse caso, dizemos que o raio de convergência é$R=∞$.
- iii. Existe um número real R tal que a série converge$|x−a|<R$ e diverge para$|x−a|>R$. Nesse caso, o raio de convergência é$R.$
Se uma série de potências converge em um intervalo finito, a série pode ou não convergir nas extremidades.
O teste de proporção geralmente pode ser usado para determinar o raio de convergência.
A série geométrica$\displaystyle \sum_{n=0}^∞x^n=\dfrac{1}{1−x}$ para nos$|x|<1$ permite representar certas funções usando séries geométricas.

Equações-chave

Série Power centrada em$x=0$

\[ \sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots n\nonumber \]

Série Power centrada em$x=a$

\[ \sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

Glossário

intervalo de convergência: o conjunto de números reais$x$ para os quais uma série de potências converge

série power: uma série da forma$\displaystyle \sum_{n=0}^∞c_nx^n$ é uma série de potências centrada em$x=0$; uma série da forma$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ é uma série de potências centrada em$x=a$

raio de convergência: se existe um número real$R>0$ tal que uma série de potências centrada em$x=a$ converge$|x−a|<R$ e diverge para$|x−a|>R$, então$R$ é o raio de convergência; se a série de potências converge apenas em$x=a$, o raio de convergência é$R=0$; se a série de potências converge para todos os números reais$x$, o raio de convergência é$R=∞$

Definição\(\PageIndex{1}\): Power Series

Nota\(\PageIndex{1}\): Convergence of a Power Series

Prova

Definição: raio de convergência

Exemplo\(\PageIndex{1}\): Finding the Interval and Radius of Convergence

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): Graphing a Function and Partial Sums of its Power Series

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\): Representing a Function with a Power Series

Exercício\(\PageIndex{3}\)