9.4: Testes de comparação

Objetivos de

• Use o teste de comparação para testar a convergência de uma série.
• Use o teste de comparação de limites para determinar a convergência de uma série.

Vimos que o teste integral nos permite determinar a convergência ou divergência de uma série comparando-a com uma integral imprópria relacionada. Nesta seção, mostramos como usar testes de comparação para determinar a convergência ou divergência de uma série comparando-a com uma série cuja convergência ou divergência é conhecida. Normalmente, esses testes são usados para determinar a convergência de séries que são semelhantes às séries geométricas ou\(p\) séries.

Teste de comparação

Nas duas seções anteriores, discutimos duas grandes classes de séries: séries geométricas e\(p\) séries. Sabemos exatamente quando essas séries convergem e quando elas divergem. Aqui, mostramos como usar a convergência ou divergência dessas séries para provar a convergência ou divergência para outras séries, usando um método chamado teste de comparação.

Por exemplo, considere a série

\[\sum_{n=1}^∞\dfrac{1}{n^2+1}. \nonumber \]

Esta série é semelhante à série convergente

\[\sum_{n=1}^∞\dfrac{1}{n^2} \nonumber \]

Como os termos em cada uma das séries são positivos, a sequência de somas parciais para cada série é monótona e crescente. Além disso, uma vez que

\[0<\dfrac{1}{n^2+1}<\dfrac{1}{n^2} \nonumber \]

para todos os números inteiros positivos\(n\), a soma\(k^{\text{th}}\) parcial\(S_k\) de\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2+1}\) satisfaz

\[S_k=\sum_{n=1}^k\dfrac{1}{n^2+1}<\sum_{n=1}^k\dfrac{1}{n^2}<\sum_{n=1}^∞\dfrac{1}{n^2}. \nonumber \]

(Veja a Figura\(\PageIndex{1a}\) e a Tabela\(\PageIndex{1}\).) Como a série à direita converge, a sequência\({S_k}\) é limitada acima. Concluímos que\({S_k}\) é uma sequência crescente monótona que está limitada acima. Portanto, pelo Teorema da Convergência Monótona,\({S_k}\) converge e, portanto,

\[\sum_{n=1}^∞\dfrac{1}{n^2+1} \nonumber \]

converge.

Da mesma forma, considere a série

\[\sum_{n=1}^∞\dfrac{1}{n−1/2}. \nonumber \]

Esta série é semelhante à série divergente

\[\sum_{n=1}^∞\dfrac{1}{n}. \nonumber \]

A sequência de somas parciais para cada série é monótona, aumentando e

\[\dfrac{1}{n−1/2}>\dfrac{1}{n}>0 \nonumber \]

para cada número inteiro positivo\(n\). Portanto, a soma\(k^{\text{th}}\) parcial\(S_k\) de

\[ \sum^∞_{n=1}\dfrac{1}{n−1/2} \nonumber \]

satisfaz

\[S_k=\sum_{n=1}^k\dfrac{1}{n−1/2}>\sum_{n=1}^k\dfrac{1}{n}. \nonumber \]

(Veja a Figura\(\PageIndex{1n}\) e a Tabela\(\PageIndex{1}\)). Como a série\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverge até o infinito, a sequência de somas parciais\(\displaystyle \sum^k_{n=1}\frac{1}{n}\) é ilimitada. Consequentemente,\({S_k}\) é uma sequência ilimitada e, portanto, diverge. Concluímos que

\[\sum_{n=1}^∞\dfrac{1}{n−1/2} \nonumber \]

diverge.

Figura\(\PageIndex{1}\): (a) Cada uma das somas parciais da série dada é menor que a soma parcial correspondente para a convergência\(p−series\). (b) Cada uma das somas parciais para a série dada é maior do que a soma parcial correspondente para a série harmônica divergente.

Tabela\(\PageIndex{1}\): Comparando uma série com uma\(p\) série -(\(p = 2\))

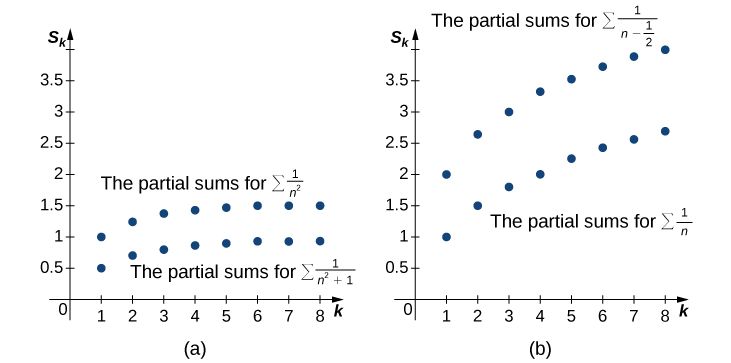
\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2+1}\)	0,5	0,7	0,8	0,8588	0,8973	0,9243	0,9443	0,9597
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2}\)	1	1,25	1.3611	1.4236	1.4636	1.4914	1.5118	1.5274

Tabela\(\PageIndex{2}\): Comparando uma série com a série harmônica

\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n−1/2}\)	2	2.667	3.0667	3,3524	3.5746	3.7564	3.9103	4.0436
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n}\)	1	1,5	1.8333	2.0933	2.283	2,45	2.5929	2.7179

Teste de comparação

1. Suponha que exista um número inteiro\(N\) such that \(0≤a_n≤b_n\) for all \(n≥N\). If \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges.
2. Suponha que exista um número inteiro\(N\) such that \(a_n≥b_n≥0\) for all \(n≥N.\) If \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.

Prova

Provamos a parte i. A prova da parte ii. é o contrapositivo da parte i. Vamos\({S_k}\) be the sequence of partial sums associated with \(\displaystyle \sum^∞_{n=1}a_n\), and let \(\displaystyle L=\sum^∞_{n=1}b_n\). Since the terms \(a_n≥0,\)

\[S_k=a_1+a_2+⋯+a_k≤a_1+a_2+⋯+a_k+a_{k+1}=S_{k+1}. \nonumber \]

Portanto, a sequência de somas parciais está aumentando. Além disso, uma vez que\(a_n≤b_n\) for all \(n≥N\), then

\[\sum_{n=N}^ka_n≤\sum_{n=N}^kb_n≤\sum_{n=1}^∞b_n=L. \nonumber \]

Portanto, para todos\(k≥1\),

\[S_k=(a_1+a_2+⋯+a_{N−1})+\sum_{n=N}^ka_n≤(a_1+a_2+⋯+a_{N−1})+L. \nonumber \]

Desde\(a_1+a_2+⋯+a_{N−1}\) is a finite number, we conclude that the sequence \({S_k}\) is bounded above. Therefore, \({S_k}\) is an increasing sequence that is bounded above. By the Monotone Convergence Theorem, we conclude that \({S_k}\) converges, and therefore the series \(\displaystyle \sum_{n=1}^∞a_n\) converges.

□

Para usar o teste de comparação para determinar a convergência ou divergência de uma série\(\displaystyle \sum_{n=1}^∞a_n\), it is necessary to find a suitable series with which to compare it. Since we know the convergence properties of geometric series and \(p\)-series, these series are often used. If there exists an integer \(N\) such that for all \(n≥N\), each term an is less than each corresponding term of a known convergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) converges. Similarly, if there exists an integer \(N\) such that for all \(n≥N\), each term an is greater than each corresponding term of a known divergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) diverges.

Exemplo\(\PageIndex{1}\): Using the Comparison Test

Para cada uma das séries a seguir, use o teste de comparação para determinar se a série converge ou diverge.

1. \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{n^3+3n+1}\)
2. \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{2^n+1}\)
3. \(\displaystyle \sum_{n=2}^∞=\dfrac{1}{\ln \,n }\)

Solução

a. Compare com\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\). Como\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\) é uma\(p\) série C com\(p=3\), ela converge. Além disso,

\[\dfrac{1}{n^3+3n+1}<\dfrac{1}{n^3} \nonumber \]

para cada número inteiro positivo\(n\). Portanto, podemos concluir que\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^3+3n+1}\) converge.

b. Compare com\(\displaystyle \sum^∞_{n=1}\left(\dfrac{1}{2}\right)^n\). Como\(\displaystyle \sum_{n=1}^∞\left(\dfrac{1}{2}\right)^n\) é uma série geométrica com\(r=\dfrac{1}{2}\) e\(\left|\dfrac{1}{2}\right|<1\), ela converge. Além disso,

\[\dfrac{1}{2^n+1}<\dfrac{1}{2^n} \nonumber \]

para cada número inteiro positivo\(n\). Portanto, vemos que\(\displaystyle \sum^∞_{n=1}\dfrac{1}{2^n+1}\) converge.

c. Compare com\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\). Desde

\[\dfrac{1}{\ln n }>\dfrac{1}{n} \nonumber \]

para cada número inteiro\(n≥2\) e\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\) diverge, temos que\(\displaystyle \sum^∞_{n=2}\dfrac{1}{\ln n}\) diverge.

Exercício\(\PageIndex{1}\)

Use o teste de comparação para determinar se a série\(\displaystyle \sum^∞_{n=1}\dfrac{n}{n^3+n+1}\) converge ou diverge.

Dica

Encontre um valor\(p\) como esse\(\dfrac{n}{n^3+n+1}≤\dfrac{1}{n^p}\).

Resposta

A série converge.

Teste de comparação de limites

O teste de comparação funciona bem se pudermos encontrar uma série comparável que satisfaça a hipótese do teste. No entanto, às vezes, encontrar uma série apropriada pode ser difícil. Considere a série

\[\sum_{n=2}^∞\dfrac{1}{n^2−1}. \nonumber \]

É natural comparar esta série com a série convergente

\[\sum_{n=2}^∞\dfrac{1}{n^2}. \nonumber \]

No entanto, esta série não satisfaz a hipótese necessária para usar o teste de comparação porque

\[\dfrac{1}{n^2−1}>\dfrac{1}{n^2} \nonumber \]

para todos os números inteiros\(n≥2\). Embora pudéssemos procurar uma série diferente com a qual comparar,\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1},\) mostramos como podemos usar o teste de comparação de limites para comparar.

\[\sum_{n=2}^∞\frac{1}{n^2−1} \nonumber \]

e

\[\sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]

Vamos examinar a ideia por trás do teste de comparação de limites. Considere duas séries\(\displaystyle \sum^∞_{n=1}a_n\)\(\displaystyle \sum^∞_{n=1}b_n\) e. com termos positivos\(a_n\) e\(b_n\) e avalie

\[\lim_{n→∞}\frac{a_n}{b_n}. \nonumber \]

E se

\[\lim_{n→∞}\frac{a_n}{b_n}=L≠0, \nonumber \]

então, para um tamanho\(n\) suficientemente grande,\(a_n≈Lb_n\). Portanto, as duas séries convergem ou as duas séries divergem. Para a série\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1}\) e\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n^2}\), vemos que

\[\lim_{n→∞}\dfrac{1/(n^2−1)}{1/n^2}=\lim_{n→∞}\dfrac{n^2}{n^2−1}=1. \nonumber \]

Como\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2}\) converge, concluímos que

\[\sum_{n=2}^∞\dfrac{1}{n^2−1} \nonumber \]

converge.

O teste de comparação de limites pode ser usado em outros dois casos. Suponha

\[\lim_{n→∞}\dfrac{a_n}{b_n}=0. \nonumber \]

Nesse caso,\({a_n/b_n}\) é uma sequência limitada. Como resultado, existe uma constante\(M\) como essa\(a_n≤Mb_n\). Portanto, se\(\displaystyle \sum^∞_{n=1}b_n\) converge, então\(\displaystyle \sum^∞_{n=1}a_n\) converge. Por outro lado, suponha

\[\lim_{n→∞}\dfrac{a_n}{b_n}=∞. \nonumber \]

Nesse caso,\({a_n/b_n}\) é uma sequência ilimitada. Portanto, para cada constante\(M\) existe um número inteiro\(N\) tal que\(a_n≥Mb_n\) para todas\(n≥N.\) Portanto, se\(\displaystyle \sum^∞_{n=1}b_n\) diverge, então\(\displaystyle \sum^∞_{n=1}a_n\) diverge também.

Teste de comparação de limites

Deixe\(a_n,b_n≥0\) para todos\(n≥1.\)

1. Se\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=L≠0,\) então\(\displaystyle \sum^∞_{n=1}a_n\) e\(\displaystyle \sum^∞_{n=1}b_n\) ambos convergirem ou ambos divergirem.
2. Se\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=0\) e\(\displaystyle \sum^∞_{n=1}b_n\) convergir, então\(\displaystyle \sum^∞_{n=1}a_n\) converge.
3. Se\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=∞\) e\(\displaystyle \sum^∞_{n=1}b_n\) diverge, então\(\displaystyle \sum^∞_{n=1}a_n\) diverge.

Observe que, se\(\dfrac{a_n}{b_n}→0\) e\(\displaystyle \sum^∞_{n=1}b_n\) divergir, o teste de comparação de limites não fornece nenhuma informação. Da mesma forma, se\(\dfrac{a_n}{b_n}→∞\) e\(\displaystyle \sum^∞_{n=1}b_n\) convergir, o teste também não fornece nenhuma informação. Por exemplo, considere as duas séries\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\)\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) e. Essas séries são ambas\(p\) séries com\(p=\frac{1}{2}\) e\(p=2\), respectivamente. Já que\(p=\frac{1}{2}<1,\) a série\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) diverge. Por outro lado, desde então\(p=2>1\), a série\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) converge. No entanto, suponha que tentamos aplicar o teste de comparação de limites, usando a \(p\)série −convergente\(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\) como nossa série de comparação. Primeiro, vemos que

\[\dfrac{1/\sqrt{n}}{1/n^3}=\dfrac{n^3}{\sqrt{n}}=n^{5/2}→∞\; \text{ as } \;n→∞. \nonumber \]

Da mesma forma, vemos que

\[\dfrac{1/n^2}{1/n^3}=n→∞\; \text{ as } \;n→∞. \nonumber \]

Portanto, se\(\dfrac{a_n}{b_n}→∞\) quando\(\displaystyle \sum_{n=1}^∞b_n\) converge, não obtemos nenhuma informação sobre a convergência ou divergência de\(\displaystyle \sum_{n=1}^∞a_n\).

Exemplo\(\PageIndex{2}\): Using the Limit Comparison Test

Para cada uma das séries a seguir, use o teste de comparação de limites para determinar se a série converge ou diverge. Se o teste não se aplicar, diga isso.

1. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\)
2. \(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\)
3. \(\displaystyle \sum^∞_{n=1}\dfrac{\ln(n)}{n^2}\)

Solução

a. Compare esta série com\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\). Calcular

\(\displaystyle \lim_{n→∞}\dfrac{1/(\sqrt{n}+1)}{1/\sqrt{n}}=\lim_{n→∞}\dfrac{\sqrt{n}}{\sqrt{n}+1}=\lim_{n→∞}\dfrac{1/\sqrt{n}}{1+1/\sqrt{n}}=1.\)

Pelo teste de comparação de limites, uma vez que\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\) diverge, depois\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\) diverge.

b. Compare esta série com\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\). Nós vemos isso

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=\lim_{n→∞}\dfrac{2^n+1}{3^n}⋅\dfrac{3^n}{2^n}=\lim_{n→∞}\dfrac{2^n+1}{2^n}=\lim_{n→∞}\left[1+\left(\tfrac{1}{2}\right)^n\right]=1.\)

Portanto,

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=1.\)

Como\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\) converge, concluímos que\(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\) converge.

c. Uma vez que\(\ln n<n,\) compare com\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\). Nós vemos isso

\(\displaystyle \lim_{n→∞}\dfrac{\ln n/n^2}{1/n}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n}{1}=\lim_{n→∞}\dfrac{\ln n}{n}.\)

Para avaliar\(\displaystyle \lim_{n→∞}\ln n/n\), avalie o limite a partir\(x→∞\) da função de valor real\(\ln(x)/x\). Esses dois limites são iguais e fazer essa mudança nos permite usar a regra de L'Hôpital. Nós obtemos

\(\displaystyle \lim_{x→∞}\dfrac{lnx}{x}=\lim_{x→∞}\dfrac{1}{x}=0.\)

Portanto\(\displaystyle \lim_{n→∞}\frac{\ln n}{n}=0\), e, consequentemente,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n}=0.\)

Como o limite é,\(0\) mas\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\) diverge, o teste de comparação de limites não fornece nenhuma informação.

\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\)Em vez disso, compare com. Nesse caso,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^2}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^2}{1}=\lim_{n→∞}\ln n=∞.\)

Como o limite é,\(∞\) mas\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) converge, o teste ainda não fornece nenhuma informação.

Então, agora vamos tentar uma série entre as duas que já experimentamos. Escolhendo a série\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\), vemos que

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^{3/2}}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^{3/2}}{1}=\lim_{n→∞}\dfrac{\ln n}{\sqrt{n}}\).

Como acima, para avaliar\(\displaystyle \lim_{n→∞}\frac{\ln n}{\sqrt{n}}\), avalie o limite a partir\(x→∞\) da função de valor real\(\frac{\ln n}{\sqrt{n}}\). Usando a regra de L'Hôpital,

\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{\sqrt{x}}=\lim_{x→∞}\dfrac{2\sqrt{x}}{x}=\lim_{x→∞}\dfrac{2}{\sqrt{x}}=0\).

Como o limite é\(0\) e\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\) converge, podemos concluir que\(\displaystyle \sum^∞_{n=1}\dfrac{\ln n}{n^2}\) converge.

Exercício\(\PageIndex{2}\)

Use o teste de comparação de limites para determinar se a série\(\displaystyle \sum^∞_{n=1}\dfrac{5^n}{3^n+2}\) converge ou diverge.

Dica

Compare com uma série geométrica.

Resposta

A série diverge.

Conceitos chave

• Os testes de comparação são usados para determinar a convergência ou divergência de séries com termos positivos.
• Ao usar os testes de comparação, uma série geralmente\(\displaystyle \sum^∞_{n=1}a_n\) é comparada a uma série geométrica ou\(p\) -série.

Glossário

teste de comparação

Se\(0≤a_n≤b_n\) para todos\(n≥N\) e\(\displaystyle \sum^∞_{n=1}b_n\) converge, então\(\displaystyle \sum^∞_{n=1}a_n\) converge; se\(a_n≥b_n≥0\) para todos\(n≥N\) e\(\displaystyle \sum^∞_{n=1}b_n\) diverge, então\(\displaystyle \sum^∞_{n=1}a_n\) diverge.

teste de comparação de limites

Suponha que\(a_n,b_n≥0\) para todos\(n≥1\). Se\(\displaystyle \lim_{n→∞}a_n/b_n→L≠0\), então\(\displaystyle \sum^∞_{n=1}a_n\) e\(\displaystyle \sum^∞_{n=1}b_n\) ambos convergem ou ambos divergem; se\(\displaystyle \lim_{n→∞}a_n/b_n→0\) e\(\displaystyle \sum^∞_{n=1}b_n\) convergir, então\(\displaystyle \sum^∞_{n=1}a_n\) converge. Se\(\displaystyle \lim_{n→∞}a_n/b_n→∞\), e\(\displaystyle \sum^∞_{n=1}b_n\) diverge, então\(\displaystyle \sum^∞_{n=1}a_n\) diverge.