8.1: Noções básicas de equações diferenciais
- Page ID
- 188030
- Identifique a ordem de uma equação diferencial.
- Explique o que significa uma solução para uma equação diferencial.
- Faça a distinção entre a solução geral e uma solução específica de uma equação diferencial.
- Identifique um problema de valor inicial.
- Identifique se uma determinada função é uma solução para uma equação diferencial ou um problema de valor inicial.
O cálculo é a matemática da mudança, e as taxas de mudança são expressas por derivadas. Assim, uma das formas mais comuns de usar o cálculo é configurar uma equação contendo uma função desconhecida\(y=f(x)\) e sua derivada, conhecida como equação diferencial. A resolução dessas equações geralmente fornece informações sobre como as quantidades mudam e frequentemente fornece uma visão sobre como e por que as mudanças ocorrem.
As técnicas para resolver equações diferenciais podem assumir muitas formas diferentes, incluindo solução direta, uso de gráficos ou cálculos computacionais. Apresentaremos as ideias principais neste capítulo e as descreveremos com um pouco mais de detalhes posteriormente no curso. Nesta seção, estudamos o que são equações diferenciais, como verificar suas soluções, alguns métodos usados para resolvê-las e alguns exemplos de equações comuns e úteis.
Equações diferenciais gerais
Considere a equação\(y′=3x^2,\) que é um exemplo de equação diferencial porque inclui uma derivada. Existe uma relação entre as variáveis\(x\) e\(y:y\) é uma função desconhecida de\(x\). Além disso, o lado esquerdo da equação é a derivada de\(y\). Portanto, podemos interpretar essa equação da seguinte forma: Comece com alguma função\(y=f(x)\) e pegue sua derivada. A resposta deve ser igual\(3x^2\) a. Qual função tem uma derivada igual a\(3x^2\)? Uma dessas funções é\(y=x^3\), então essa função é considerada uma solução para uma equação diferencial.
Uma equação diferencial é uma equação que envolve uma função desconhecida\(y=f(x)\) e uma ou mais de suas derivadas. Uma solução para uma equação diferencial é uma função\(y=f(x)\) que satisfaz a equação diferencial quando\(f\) e suas derivadas são substituídas na equação.
Acesse este site para explorar mais sobre esse tópico.
Alguns exemplos de equações diferenciais e suas soluções aparecem na Tabela\(\PageIndex{1}\).
| Equação | Solução |
|---|---|
| \(y'=2x\) | \(y=x^2\) |
| \(y'+3y=6x+11\) | \(y=e^{−3x}+2x+3\) |
| \(y''−3y'+2y=24e^{−2x}\) | \(y=3e^x−4e^{2x}+2e^{−2x}\) |
Observe que uma solução para uma equação diferencial não é necessariamente única, principalmente porque a derivada de uma constante é zero. Por exemplo, também\(y=x^2+4\) é uma solução para a primeira equação diferencial na Tabela\(\PageIndex{1}\). Voltaremos a essa ideia um pouco mais adiante nesta seção. Por enquanto, vamos nos concentrar no que significa para uma função ser uma solução para uma equação diferencial.
Verifique se a função\(y=e^{−3x}+2x+3\) é uma solução para a equação diferencial\(y′+3y=6x+11\).
Solução
Para verificar a solução, primeiro calculamos\(y′\) usando a regra da cadeia para derivadas. Isso dá\(y′=−3e^{−3x}+2\). Em seguida,\(y′\) substituímos\(y\) e no lado esquerdo da equação diferencial:
\((−3e^{−2x}+2)+3(e^{−2x}+2x+3).\)
A expressão resultante pode ser simplificada distribuindo primeiro para eliminar os parênteses, fornecendo
\(−3e^{−2x}+2+3e^{−2x}+6x+9.\)
A combinação de termos semelhantes leva à expressão\(6x+11\), que é igual ao lado direito da equação diferencial. Esse resultado verifica que\(y=e^{−3x}+2x+3\) é uma solução da equação diferencial.
Verifique se\(y=2e^{3x}−2x−2\) é uma solução para a equação diferencial\(y′−3y=6x+4.\)
- Dica
-
Primeiro calcule e,\(y\) em\(y′\) seguida, substitua os dois\(y′\) e no lado esquerdo.
É conveniente definir características das equações diferenciais que facilitem falar sobre elas e categorizá-las. A característica mais básica de uma equação diferencial é sua ordem.
A ordem de uma equação diferencial é a ordem mais alta de qualquer derivada da função desconhecida que aparece na equação.
A derivada mais alta na equação é\(y′\),
Qual é a ordem de cada uma das seguintes equações diferenciais?
- \(y′−4y=x^2−3x+4\)
- \(x^2y'''−3xy''+xy′−3y=\sin x\)
- \(\frac{4}{x}y^{(4)}−\frac{6}{x^2}y''+\frac{12}{x^4}y=x^3−3x^2+4x−12\)
Solução
- A derivada mais alta na equação é\(y′\), então a ordem é\(1\).
- A derivada mais alta na equação é\(y'''\), então a ordem é\(3\).
- A derivada mais alta na equação é\(y^{(4)}\), então a ordem é\(4\).
Qual é a ordem da seguinte equação diferencial?
\((x^4−3x)y^{(5)}−(3x^2+1)y′+3y=\sin x\cos x\)
- Dica
-
Qual é a derivada mais alta na equação?
- Resposta
-
\(5\)
Soluções gerais e particulares
Já observamos que a equação diferencial\(y′=2x\) tem pelo menos duas soluções:\(y=x^2\)\(y=x^2+4\) e. A única diferença entre essas duas soluções é o último termo, que é uma constante. E se o último termo for uma constante diferente? Essa expressão ainda será uma solução para a equação diferencial? Na verdade, qualquer função da forma\(y=x^2+C\), onde\(C\) representa qualquer constante, também é uma solução. A razão é que a derivada de\(x^2+C\) é\(2x\), independentemente do valor de\(C\). Pode-se mostrar que qualquer solução dessa equação diferencial deve ser da forma\(y=x^2+C\). Este é um exemplo de uma solução geral para uma equação diferencial. Um gráfico de algumas dessas soluções é fornecido na Figura\(\PageIndex{1}\). (Nota: neste gráfico, usamos valores inteiros pares para C variando entre\(−4\)\(4\) e. Na verdade, não há nenhuma restrição quanto ao valor de\(C\); ele pode ser um número inteiro ou não.)
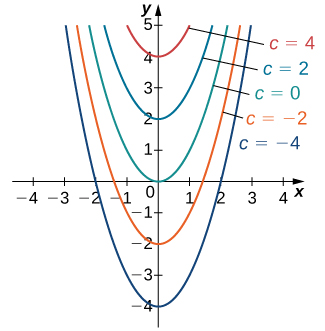
Neste exemplo, somos livres para escolher qualquer solução que desejamos; por exemplo,\(y=x^2−3\) é membro da família de soluções para essa equação diferencial. Isso é chamado de uma solução específica para a equação diferencial. Muitas vezes, uma solução específica pode ser identificada de forma exclusiva se recebermos informações adicionais sobre o problema.
Encontre a solução específica para a equação diferencial\(y′=2x\) que passa pelo ponto\((2,7)\).
Solução
Qualquer função da forma\(y=x^2+C\) é uma solução para essa equação diferencial. Para determinar o valor de\(C\), substituímos os valores\(x=2\) e\(y=7\) nesta equação e resolvemos por\(C\):
\[ \begin{align*} y =x^2+C \\[4pt] 7 =2^2+C \\[4pt] =4+C \\[4pt] C =3. \end{align*}\]
Portanto, a solução específica que passa pelo ponto\((2,7)\) é\(y=x^2+3\).
Encontre a solução específica para a equação diferencial
\[ y′=4x+3 \nonumber \]
passando pelo ponto\((1,7),\) dado que\(y=2x^2+3x+C\) é uma solução geral para a equação diferencial.
- Dica
-
Primeiro substitua\(x=1\) e\(y=7\) entre na equação, depois resolva por\(C\).
- Resposta
-
\[ y=2x^2+3x+2 \nonumber \]
Problemas de valor inicial
Normalmente, uma determinada equação diferencial tem um número infinito de soluções, então é natural perguntar qual delas queremos usar. Para escolher uma solução, são necessárias mais informações. Algumas informações específicas que podem ser úteis são um valor inicial, que é um par ordenado usado para encontrar uma solução específica.
Uma equação diferencial junto com um ou mais valores iniciais é chamada de problema de valor inicial. A regra geral é que o número de valores iniciais necessários para um problema de valor inicial é igual à ordem da equação diferencial. Por exemplo, se tivermos a equação diferencial\(y′=2x\), então\(y(3)=7\) é um valor inicial e, quando consideradas em conjunto, essas equações formam um problema de valor inicial. A equação diferencial\(y''−3y′+2y=4e^x\) é de segunda ordem, então precisamos de dois valores iniciais. Com problemas de valor inicial de ordem maior que um, o mesmo valor deve ser usado para a variável independente. Um exemplo de valores iniciais para essa equação de segunda ordem seria\(y(0)=2\) e\(y′(0)=−1.\) Esses dois valores iniciais junto com a equação diferencial formam um problema de valor inicial. Esses problemas têm esse nome porque geralmente a variável independente na função desconhecida é\(t\), que representa o tempo. Assim, um valor de\(t=0\) representa o início do problema.
Verifique se a função\(y=2e^{−2t}+e^t\) é uma solução para o problema do valor inicial
\[ y′+2y=3e^t, \quad y(0)=3.\nonumber \]
Solução
Para que uma função satisfaça um problema de valor inicial, ela deve satisfazer tanto a equação diferencial quanto a condição inicial. Para mostrar que\(y\) satisfaz a equação diferencial, começamos calculando\(y′\). Isso dá\(y′=−4e^{−2t}+e^t\). Em seguida, substituímos ambos\(y\) e\(y′\) no lado esquerdo da equação diferencial e simplificamos:
\[ \begin{align*} y′+2y &=(−4e^{−2t}+e^t)+2(2e^{−2t}+e^t) \\[4pt] &=−4e^{−2t}+e^t+4e^{−2t}+2e^t =3e^t. \end{align*}\]
Isso é igual ao lado direito da equação diferencial, então\(y=2e^{−2t}+e^t\) resolve a equação diferencial. Em seguida, calculamos\(y(0)\):
\[ y(0)=2e^{−2(0)}+e^0=2+1=3. \nonumber \]
Esse resultado verifica o valor inicial. Portanto, a função fornecida satisfaz o problema do valor inicial.
Verifique se\(y=3e^{2t}+4\sin t\) é uma solução para o problema do valor inicial
\[ y′−2y=4\cos t−8\sin t,y(0)=3. \nonumber \]
- Dica
-
Primeiro, verifique se isso\(y\) resolve a equação diferencial. Em seguida, verifique o valor inicial.
No exemplo\(\PageIndex{4}\), o problema do valor inicial consistia em duas partes. A primeira parte foi a equação diferencial\(y′+2y=3e^x\), e a segunda parte foi o valor inicial.\(y(0)=3.\) Essas duas equações juntas formaram o problema do valor inicial.
O mesmo é verdade em geral. Um problema de valor inicial consistirá em duas partes: a equação diferencial e a condição inicial. A equação diferencial tem uma família de soluções e a condição inicial determina o valor de\(C\). A família de soluções para a equação diferencial no Exemplo\(\PageIndex{4}\) é dada por\(y=2e^{−2t}+Ce^t.\) Esta família de soluções é mostrada na Figura\(\PageIndex{2}\), com a solução específica\(y=2e^{−2t}+e^t\) rotulada.
Resolva o seguinte problema de valor inicial:
\[ y′=3e^x+x^2−4,y(0)=5. \nonumber \]
Solução
A primeira etapa para resolver esse problema de valor inicial é encontrar uma família geral de soluções. Para fazer isso, encontramos uma antiderivada de ambos os lados da equação diferencial
\[∫y′\,dx=∫(3e^x+x^2−4)\,dx, \nonumber \]
nomeadamente,
\(y+C_1=3e^x+\frac{1}{3}x^3−4x+C_2\).
Somos capazes de integrar os dois lados porque o termo y aparece por si só. Observe que há duas constantes de integração:\(C_1\)\(C_2\) e. Resolvendo essa equação para\(y\) dados
\(y=3e^x+\frac{1}{3}x^3−4x+C_2−C_1.\)
Porque\(C_1\) e\(C_2\) são ambas constantes, também\(C_2−C_1\) é uma constante. Portanto, podemos definir\(C=C_2−C_1,\) o que leva à equação.
\(y=3e^x+\frac{1}{3}x^3−4x+C.\)
Em seguida, determinamos o valor de\(C\). Para fazer isso, substituímos\(x=0\) e\(y=5\) entramos nessa equação e resolvemos por\(C\):
\[ \begin{align*} 5 &=3e^0+\frac{1}{3}0^3−4(0)+C \\[4pt] 5 &=3+C \\[4pt] C&=2 \end{align*}. \nonumber \]
Agora substituímos o valor\(C=2\) na equação geral. A solução para o problema do valor inicial é\(y=3e^x+\frac{1}{3}x^3−4x+2.\)
Análise
A diferença entre uma solução geral e uma solução específica é que uma solução geral envolve uma família de funções, definidas explícita ou implicitamente, da variável independente. O valor ou valores iniciais determinam qual solução específica na família de soluções satisfaz as condições desejadas.
Resolva o problema do valor inicial
\[ y′=x^2−4x+3−6e^x,y(0)=8. \nonumber \]
- Dica
-
Primeiro, pegue a antiderivada de ambos os lados da equação diferencial. Em seguida, substitua\(x=0\) e\(y=8\) na equação resultante e resolva por\(C\).
- Resposta
-
\(y=\frac{1}{3}x^3−2x^2+3x−6e^x+14\)
Em aplicações de física e engenharia, geralmente consideramos as forças que atuam sobre um objeto e usamos essas informações para entender o movimento resultante que pode ocorrer. Por exemplo, se começarmos com um objeto na superfície da Terra, a força primária que atua sobre esse objeto é a gravidade. Físicos e engenheiros podem usar essas informações, junto com a segunda lei do movimento de Newton (em forma de equação\(F=ma\), onde\(F\) representa força,\(m\) representa massa e\(a\) representa aceleração), para derivar uma equação que pode ser resolvida.
Na Figura,\(\PageIndex{3}\) assumimos que a única força atuando em uma bola de beisebol é a força da gravidade. Essa suposição ignora a resistência do ar. (A força devida à resistência do ar é considerada em uma discussão posterior.) A aceleração devido à gravidade na superfície da Terra, g, é de aproximadamente\(9.8\,\text{m/s}^2\). Introduzimos um quadro de referência, onde a superfície da Terra está a uma altura de 0 metros. Vamos\(v(t)\) representar a velocidade do objeto em metros por segundo. Se\(v(t)>0\), a bola está subindo e, se\(v(t)<0\), a bola está caindo (Figura).
Nosso objetivo é resolver a velocidade a qualquer\(v(t)\) momento\(t\). Para fazer isso, configuramos um problema de valor inicial. Suponha que a massa da bola seja\(m\), onde\(m\) é medida em quilogramas. Usamos a segunda lei de Newton, que afirma que a força que atua sobre um objeto é igual à sua massa vezes sua aceleração\((F=ma)\). A aceleração é a derivada da velocidade, então\(a(t)=v′(t)\). Portanto, a força que atua no beisebol é dada por\(F=mv′(t)\). No entanto, essa força deve ser igual à força da gravidade que atua sobre o objeto, que (novamente usando a segunda lei de Newton) é dada por\(F_g=−mg\), uma vez que essa força atua na direção descendente. Portanto, obtemos a equação\(F=F_g\), que se torna\(mv′(t)=−mg\). Dividindo os dois lados da equação por\(m\) fornece a equação
\[ v′(t)=−g. \nonumber \]
Observe que essa equação diferencial permanece a mesma, independentemente da massa do objeto.
Agora precisamos de um valor inicial. Como estamos resolvendo a velocidade, faz sentido, no contexto do problema, supor que sabemos a velocidade inicial, ou a velocidade no momento.\(t=0.\) Isso é denotado por\(v(0)=v_0.\)
Uma bola de beisebol é lançada para cima de uma altura de\(3\) metros acima da superfície da Terra com uma velocidade inicial de\(10\) m/s, e a única força atuando nela é a gravidade. A bola tem uma massa de\(0.15\) kg na superfície da Terra.
- Determine a velocidade\(v(t)\) da bola de base ao mesmo tempo\(t\).
- Qual é sua velocidade após\(2\) segundos?
Solução
a. Da discussão anterior, a equação diferencial que se aplica nessa situação é
\(v′(t)=−g,\)
onde\(g=9.8\, \text{m/s}^2\). A condição inicial é\(v(0)=v_0\), onde\(v_0=10\) m/s. Portanto, o problema do valor inicial é\(v′(t)=−9.8\,\text{m/s}^2,\,v(0)=10\) m/s.
O primeiro passo para resolver esse problema de valor inicial é usar a antiderivada de ambos os lados da equação diferencial. Isso dá
\[\int v′(t)\,dt=∫−9.8\,dt \nonumber \]
\(v(t)=−9.8t+C.\)
A próxima etapa é resolver\(C\) o. Para fazer isso, substitua\(t=0\) e\(v(0)=10\):
\[ \begin{align*} v(t) &=−9.8t+C \\[4pt] v(0) &=−9.8(0)+C \\[4pt] 10 &=C. \end{align*}\]
Portanto,\(C=10\) e a função de velocidade é dada por\(v(t)=−9.8t+10.\)
b. Para encontrar a velocidade após\(2\) segundos,\(t=2\) substitua por\(v(t)\).
\[ \begin{align*} v(t)&=−9.8t+10 \\[4pt] v(2)&=−9.8(2)+10 \\[4pt] v(2) &=−9.6\end{align*}\]
As unidades de velocidade são metros por segundo. Como a resposta é negativa, o objeto está caindo a uma velocidade de\(9.6\) m/s.
Suponha que uma rocha caia do repouso de uma altura de\(100\) metros e a única força atuando nela seja a gravidade. Encontre uma equação para a velocidade\(v(t)\) em função do tempo, medida em metros por segundo.
- Dica
-
Qual é a velocidade inicial da rocha? Use isso com a equação diferencial em Example\(\PageIndex{6}\) para formar um problema de valor inicial e, em seguida, resolva\(v(t)\).
- Resposta
-
\(v(t)=−9.8t\)
Uma pergunta natural a ser feita depois de resolver esse tipo de problema é a altura do objeto acima da superfície da Terra em um determinado momento. Vamos\(s(t)\) indicar a altura acima da superfície da Terra do objeto, medida em metros. Como a velocidade é a derivada da posição (neste caso a altura), essa suposição fornece a equação\(s′(t)=v(t)\). É necessário um valor inicial; nesse caso, a altura inicial do objeto funciona bem. Deixe a altura inicial ser dada pela equação\(s(0)=s_0\). Juntas, essas suposições dão o problema do valor inicial.
\[ s′(t)=v(t),s(0)=s_0. \nonumber \]
Se a função de velocidade for conhecida, então também é possível resolver a função de posição.
Uma bola de beisebol é lançada para cima de uma altura de\(3\) metros acima da superfície da Terra com uma velocidade inicial de\(10m/s\), e a única força atuando nela é a gravidade. A bola tem uma massa de\(0.15\) quilograma na superfície da Terra.
- Encontre a posição\(s(t)\) da bola de beisebol por vez\(t\).
- Qual é sua altura após\(2\) alguns segundos?
Solução
Já sabemos que a função de velocidade para esse problema é\(v(t)=−9.8t+10\). A altura inicial da bola de beisebol é de\(3\) metros, então\(s_0=3\). Portanto, o problema do valor inicial para este exemplo é
Para resolver o problema do valor inicial, primeiro encontramos as antiderivadas:
\[∫s′(t)\,dt=∫(−9.8t+10)\,dt \nonumber \]
\(s(t)=−4.9t^2+10t+C.\)
Em seguida, substituímos\(t=0\) e resolvemos por\(C\):
\(s(t)=−4.9t^2+10t+C\)
\(s(0)=−4.9(0)^2+10(0)+C\)
\(3=C\).
Portanto, a função de posição é\(s(t)=−4.9t^2+10t+3.\)
b. A altura da bola de beisebol após o\(2\) segundo é dada por\(s(2):\)
\(s(2)=−4.9(2)^2+10(2)+3=−4.9(4)+23=3.4.\)
Portanto, a bola de beisebol está\(3.4\) metros acima da superfície da Terra após\(2\) segundos. Vale a pena notar que a massa da bola foi completamente cancelada no processo de solução do problema.
Conceitos chave
- Uma equação diferencial é uma equação que envolve uma função\(y=f(x)\) e uma ou mais de suas derivadas. Uma solução é uma função\(y=f(x)\) que satisfaz a equação diferencial quando\(f\) e suas derivadas são substituídas na equação.
- A ordem de uma equação diferencial é a ordem mais alta de qualquer derivada da função desconhecida que aparece na equação.
- Uma equação diferencial acoplada a um valor inicial é chamada de problema de valor inicial. Para resolver um problema de valor inicial, primeiro encontre a solução geral para a equação diferencial e, em seguida, determine o valor da constante. Os problemas de valor inicial têm muitas aplicações em ciência e engenharia.
Glossário
- equação diferencial
- uma equação envolvendo uma função\(y=y(x)\) e uma ou mais de suas derivadas
- solução geral (ou família de soluções)
- todo o conjunto de soluções para uma determinada equação diferencial
- valor (s) inicial (es)
- um valor ou conjunto de valores que uma solução de uma equação diferencial satisfaz para um valor fixo da variável independente
- velocidade inicial
- a velocidade no tempo\(t=0\)
- problema de valor inicial
- uma equação diferencial junto com um valor ou valores iniciais
- ordem de uma equação diferencial
- a ordem mais alta de qualquer derivada da função desconhecida que aparece na equação
- solução específica
- membro de uma família de soluções para uma equação diferencial que satisfaz uma condição inicial específica
- solução para uma equação diferencial
- uma função\(y=f(x)\) que satisfaz uma determinada equação diferencial


