7.7: Integrais impróprios

objetivos de aprendizagem

• Calcule uma integral em um intervalo infinito.
• Avalie uma integral em um intervalo fechado com uma descontinuidade infinita dentro do intervalo.
• Use o teorema da comparação para determinar se uma integral definida é convergente.

A área entre o gráfico de$f(x)=\dfrac{1}{x}$ e o$x$ eixo -no intervalo é$[1,+∞)$ finita ou infinita? Se essa mesma região é girada em torno do$x$ eixo -, o volume é finito ou infinito? Surpreendentemente, a área da região descrita é infinita, mas o volume do sólido obtido pela rotação dessa região em torno do$x$ eixo -é finito.

Nesta seção, definimos integrais em um intervalo infinito, bem como integrais de funções contendo uma descontinuidade no intervalo. Integrais desses tipos são chamados de integrais impróprios. Examinamos várias técnicas para avaliar integrais impróprias, todas envolvendo a definição de limites.

Integração em um intervalo infinito

Como devemos definir uma integral do tipo$\displaystyle \int ^{+∞}_af(x)\,dx?$ que podemos integrar$\displaystyle \int ^t_af(x)\,dx$ por qualquer valor de$t$, então é razoável observar o comportamento dessa integral à medida que substituímos valores maiores de$t$. A figura$\PageIndex{1}$ mostra que$\displaystyle \int ^t_af(x)\,dx$ pode ser interpretada como área para vários valores de$t$. Em outras palavras, podemos definir uma integral imprópria como um limite, considerado como um dos limites da integração aumenta ou diminui sem limite.

Figura$\PageIndex{1}$: Para integrar uma função em um intervalo infinito, consideramos o limite da integral à medida que o limite superior aumenta sem limite.

Definição: integral impróprio

1. $f(x)$Seja contínuo ao longo de um intervalo do formulário$[a,+∞)$. Em seguida, $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx, \label{improper1}$$ desde que esse limite exista.
2. $f(x)$Seja contínuo ao longo de um intervalo do formulário$(−∞,b]$. Em seguida, $$\int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx, \label{improper2}$$ desde que esse limite exista.

Em cada caso, se o limite existir, diz-se que a integral imprópria converge. Se o limite não existir, diz-se que a integral imprópria diverge.

3. Que$f(x)$ seja contínuo$(−∞,+∞)$. Em seguida, $$\int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx, \label{improper3}$$ desde que isso$\displaystyle \int ^0_{−∞}f(x)\,dx$ e$\displaystyle \int ^{+∞}_0f(x)\,dx$ ambos converjam. Se qualquer uma dessas duas integrais divergir, então$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx$ diverge. (Pode-se demonstrar que, de fato,$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^a_{−∞}f(x)\,dx+\int ^{+∞}_af(x)\,dx$ para qualquer valor de a.).

Em nosso primeiro exemplo, retornamos à pergunta que fizemos no início desta seção: A área entre o gráfico de$f(x)=\frac{1}{x}$ e o$x$ eixo -no intervalo é$[1,+∞)$ finita ou infinita?

Exemplo$\PageIndex{1}$: Finding an Area

Determine se a área entre o gráfico de$f(x)=\dfrac{1}{x}$ e o$x$ eixo -no intervalo$[1,+∞)$ é finita ou infinita.

Solução

Primeiro, fazemos um esboço rápido da região em questão, conforme mostrado na Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$: Podemos encontrar a área entre a curva$f(x)=1/x$ e o$x$ eixo -em um intervalo infinito.

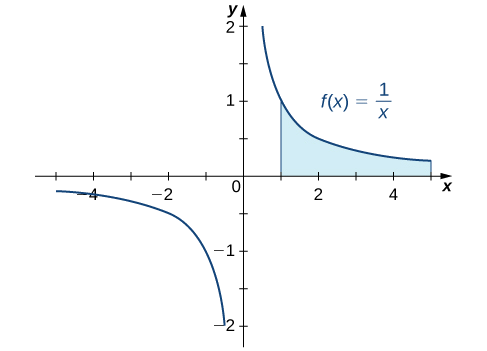
Podemos ver que a área dessa região é dada por

$$A=\int ^∞_1\frac{1}{x}\,dx. \nonumber$$

que pode ser avaliado usando a Equação\ ref {improper1}:

$$\begin{align*} A =\int ^∞_1\frac{1}{x}\,dx \nonumber \\[4pt] =\lim_{t→+∞}\int ^t_1\frac{1}{x}\,dx \tag{Rewrite the improper integral as a limit} \\[4pt] =\lim_{t→+∞}\ln |x|∣^t_1 \tag{Find the antiderivative} \\[4pt] =\lim_{t→+∞}(\ln |t|−\ln 1) \tag{Evaluate the antiderivative} \\[4pt] =+∞. \tag{Evaluate the limit.} \end{align*}$$

Como a integral imprópria diverge,$+∞,$ a área da região é infinita.

Exemplo$\PageIndex{2}$: Finding a Volume

Encontre o volume do sólido obtido girando a região delimitada pelo gráfico de$f(x)=\dfrac{1}{x}$ e o$x$ eixo$[1,+∞)$ -sobre o intervalo em torno do$x$ eixo -.

Solução

O sólido é mostrado na Figura$\PageIndex{3}$. Usando o método de disco, vemos que o volume$V$ é

$$V=π\int ^{+∞}_1\frac{1}{x^2}\,dx. \nonumber$$

Figura$\PageIndex{3}$: O sólido da revolução pode ser gerado girando uma área infinita em torno do$x$ eixo.

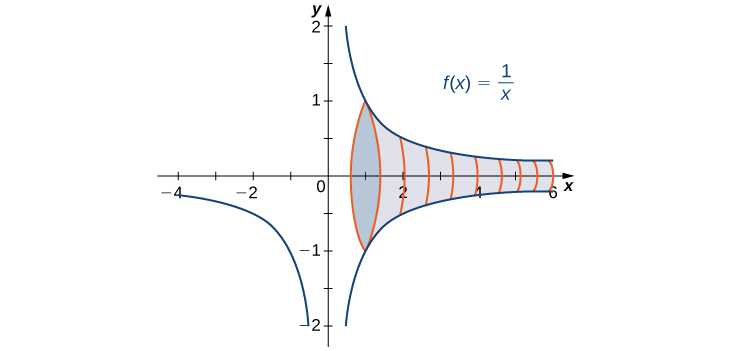
Então nós temos

\ [\ displaystyle\ begin {align*} V &=π\ int ^ {+∞} _1\ frac {1} {x^2}\, dx\\ [4pt]
&=π\ lim_ {t→+∞}\ int ^t_1\ frac {1} {x^2}\, dx\ quad\ text {Reescrever como um limite.}\\ [4pt]
&=π\ lim_ {t→+∞} −\ frac {1} {x} ^t_1\ quad\ text {Encontre a antiderivada.}\\ [4pt]
&=π\ lim_ {t→+∞}\ left (− \ frac {1} {t} +1\ right)\ quad\ text {Avalie a antiderivada.}\\ [4pt]
&=π\ end {align*}\]

A integral imprópria converge para$π$. Portanto, o volume do sólido da revolução é$π$.

Em conclusão, embora a área da região entre o$x$ eixo -e o gráfico do$f(x)=1/x$ intervalo$[1,+∞)$ seja infinita, o volume do sólido gerado pela rotação dessa região em torno do$x$ eixo -é finito. O sólido gerado é conhecido como Chifre de Gabriel.

Nota: A trompa de Gabriel (também chamada de trompete de Torricelli) é uma figura geométrica que tem área de superfície infinita, mas volume finito. O nome se refere à tradição de identificar o Arcanjo Gabriel como o anjo que toca a buzina para anunciar o Dia do Julgamento, associando o divino, ou infinito, ao finito. As propriedades dessa figura foram estudadas pela primeira vez pelo físico e matemático italiano Evangelista Torricelli no século XVII.

Exemplo$\PageIndex{3}$: Traffic Accidents in a City

Suponha que em um cruzamento movimentado, os acidentes de trânsito ocorram a uma taxa média de um a cada três meses. Depois que os moradores reclamaram, mudanças foram feitas nos semáforos no cruzamento. Já se passaram oito meses desde que as mudanças foram feitas e não houve acidentes. As mudanças foram efetivas ou o intervalo de 8 meses sem um acidente é resultado do acaso?

Figura$\PageIndex{4}$: Modificação do trabalho de David McKelvey, Flickr.

A teoria da probabilidade nos diz que, se o tempo médio entre os eventos for$k$, a probabilidade de que$X$, o tempo entre os eventos, esteja entre$a$ e$b$ seja dada por

$$(P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber$$

onde

$$f(x)=\begin{cases}0, \text{if}\;x<0\\ke^{−kx}, \text{if}\;x≥0\end{cases}. \nonumber$$

Assim, se os acidentes estão ocorrendo a uma taxa de um a cada 3 meses, então a probabilidade de que$X$, o tempo entre os acidentes, seja entre$a$ e$b$ é dada por

$$P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber$$

onde $$f(x)=\begin{cases}0, \text{if}\;x<0\\3e^{−3x}, \text{if}\;x≥0\end{cases}. \nonumber$$

Para responder à pergunta, devemos calcular$\displaystyle P(X≥8)=\int ^{+∞}_83e^{−3x}\,dx$ e decidir se é provável que 8 meses tenham passado sem um acidente se não houvesse melhora na situação do trânsito.

Solução

Precisamos calcular a probabilidade como uma integral imprópria:

\ (\ displaystyle\ begin {align*} P (X≥8) =\ int ^ {+∞} _83e^ {−3x}\, dx\\ [4pt]
=\ lim_ {t→+∞}\ int ^t_83e^ {−3x}\, dx\\ [4pt]
=\ lim_ {t→+∞} −e^ {−3x} ^t_8\\ [4pt]
=\ lim_ {t→+∞} (−e^ {−3t} +e^ {−24})\\ [4pt]
≈ 3,8 × 10^ {−11}. \ end {align*}\)

O valor$3.8×10^{−11}$ representa a probabilidade de não haver acidentes em 8 meses nas condições iniciais. Como esse valor é muito, muito pequeno, é razoável concluir que as mudanças foram efetivas.

Exemplo$\PageIndex{4}$: Evaluating an Improper Integral over an Infinite Interval

$\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx.$Avalie se a integral imprópria converge ou diverge.

Solução

Comece reescrevendo$\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx$ como um limite usando a Equação\ ref {improper2} da definição. Assim,

\ [\ begin {align*}\ int ^0_ {−∞}\ frac {1} {x^2+4}\, dx &=\ lim_ {t→−∞}\ int ^0_t\ frac {1} {x^2+4}\, dx\ quad\ text {Reescrever como um limite.}\\ [4pt]
&=\ lim_ {t→T→→ −−∞}\ frac {1} {2}\ tan^ {−1}\ frac {x} {2} ^0_t\ quad\ text {Encontre a antiderivada.}\\ [4pt]
&=\ lim_ {t→−∞}\ left (\ frac {1} {2}\ tan^ {−1} 0−\ frac {1} {2}\ tan^ {−1}\ frac {t} {2}\ right)\ quad\ text {Avalie a antiderivada.}\\ [4pt]
&=\ frac {π} {4}. \ quad\ text {Avalie o limite e simplifique.} \ end {align*}\]

A integral imprópria converge para$\dfrac{π}{4}.$

Exemplo$\PageIndex{5}$: Evaluating an Improper Integral on $(−∞,+∞)$

$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx.$Avalie se a integral imprópria converge ou diverge.

Solução

Comece dividindo a integral:

$$\int ^{+∞}_{−∞}xe^x\,dx=\int ^0_{−∞}xe^x\,dx+\int ^{+∞}_0xe^x\,dx. \nonumber$$

Se um deles$\displaystyle \int ^0_{−∞}xe^x\,dx$ ou$\displaystyle \int ^{+∞}_0xe^x\,dx$ divergir, então$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx$ diverge. Calcule cada integral separadamente. Para a primeira integral,

$\displaystyle \int ^0_{−∞}xe^x\,dx=\lim_{t→−∞}\int ^0_txe^x\,dx$Reescreva como limite.

$=\lim_{t→−∞}(xe^x−e^x)∣^0_t$Use a integração por partes para encontrar a antiderivada. (Aqui$u=x$$dv=e^x$ e.)

$=\lim_{t→−∞}(−1−te^t+e^t)$Avalie a antiderivada.

$=−1.$

Avalie o limite. Nota:$\displaystyle \lim_{t→−∞}te^t$ é indeterminado da forma$0⋅∞$. Assim,$\displaystyle \lim_{t→−∞}te^t=\lim_{t→−∞}\frac{t}{e^{−t}}=\lim_{t→−∞}\frac{−1}{e^{−t}}=\lim_{t→−∞}−e^t=0$ pela Regra de L'Hôpital.

A primeira integral imprópria converge. Para a segunda integral,

$\displaystyle \int ^{+∞}_0xe^x\,dx=\lim_{t→+∞}\int ^t_0xe^x\,dx$Reescreva como limite.

$=\lim_{t→+∞}(xe^x−e^x)∣^t_0$Encontre a antiderivada.

$=\lim_{t→+∞}(te^t−e^t+1)$Avalie a antiderivada.

$=\lim_{t→+∞}((t−1)e^t+1)$Reescrever. ($te^t−e^t$é indeterminado.)

$=+∞.$Avalie o limite.

Assim,$\displaystyle \int ^{+∞}_0xe^x\,dx$ diverge. Como essa integral diverge, também$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx$ diverge.

Exercício$\PageIndex{1}$

$\displaystyle \int ^{+∞}_{−3}e^{−x}\,dx.$Avalie se a integral imprópria converge ou diverge.

Dica

$$\int ^{+∞}_{−3}e^{−x}\,dx=\lim_{t→+∞}\int ^t_{−3}e^{−x}\,dx \nonumber$$

Resposta

Ele converge para$e^3.$

Integrando um integrando descontínuo

Agora, vamos examinar integrais de funções que contêm uma descontinuidade infinita no intervalo em que a integração ocorre. Considere uma integral da forma$\displaystyle \int ^b_af(x)\,dx,$ em que$f(x)$ é contínua$[a,b)$ e descontínua em$b$. Como a função$f(x)$ é contínua$[a,t]$ para todos os valores de$t$ satisfação$a \le t<b$, a integral$\displaystyle \int ^t_af(x)\,dx$ é definida para todos esses valores de$t$. Assim, faz sentido considerar os valores de$\displaystyle \int ^t_af(x)\,dx$ como$t$ abordagens$b$ para$a \le t<b$. Ou seja, definimos$\displaystyle \int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx$, desde que esse limite exista. A figura$\PageIndex{5}$ ilustra$\displaystyle \int ^t_af(x)\,dx$ como áreas de regiões para valores de$t$ aproximação$b$.

Figura$\PageIndex{5}$: Quando t se aproxima de b pela esquerda, o valor da área de a a t se aproxima da área de a a b.

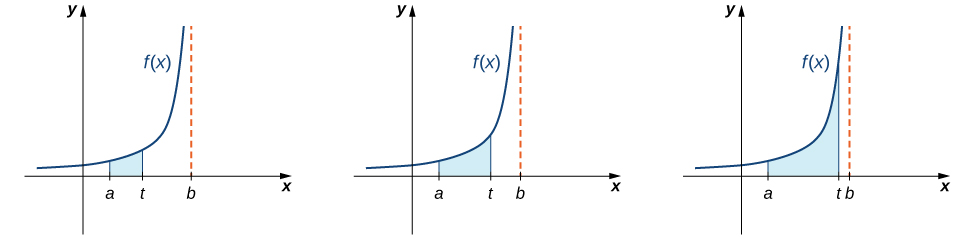
Usamos uma abordagem semelhante para definir$\displaystyle \int ^b_af(x)\,dx$ onde$f(x)$ é contínuo$(a,b]$ e descontínuo em$a$. Agora, prosseguimos com uma definição formal.

Definição: Integral impróprio convergente e divergente

1. Que$f(x)$ seja contínuo$[a,b)$. Então, $$\int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx. \label{improperundefb}$$
2. Que$f(x)$ seja contínuo$(a,b]$. Então, $$\int ^b_af(x)\,dx=\lim_{t→a^+}\int ^b_tf(x)\,dx. \label{improperundefa}$$ em cada caso, se o limite existir, diz-se que a integral imprópria converge. Se o limite não existir, diz-se que a integral imprópria diverge.
3. Se$f(x)$ for contínuo,$[a,b]$ exceto em um ponto$c$ em$(a,b)$, então $$\int ^b_af(x)\,dx=\int ^c_af(x)\,dx+\int ^b_cf(x)\,dx,\label{improperundefc}$$ forneça ambos$\displaystyle \int ^c_af(x)\,dx$ e$\displaystyle \int ^b_cf(x)\,dx$ converja. Se alguma dessas integrais divergir, então$\displaystyle \int ^b_af(x)\,dx$ diverge.

Os exemplos a seguir demonstram a aplicação dessa definição.

Exemplo$\PageIndex{6}$: Integrating a Discontinuous Integrand

Avalie$\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx,$ se possível. Indique se a integral converge ou diverge.

Solução

A função$f(x)=\dfrac{1}{\sqrt{4−x}}$ é contínua$[0,4)$ e descontínua em 4. Usando a Equação\ ref {improperundefb} da definição, reescreva$\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx$ como um limite:

\ (\ displaystyle\ begin {align*}\ int ^4_0\ frac {1} {\ sqrt {4−x}}\, dx &=\ lim_ {t→4^−}\ int ^t_0\ frac {1} {\ sqrt {4−x}}\, dx\ quad\ text {Reescrever como um limite.}\\ [4pt]
&=\ lim_ {t→4^−} (−2\ sqrt {4−x}) ^t_0\ quad\ text {Encontre a antiderivada.}\\ [4pt]
&=\ lim_ {t→4^−} (−2\ sqrt {4−t} +4)\ quad\ text {Avalie a antiderivada.}\\ [4pt]
&=4. \ quad\ text {Avalie o limite.} \ end {align*}\)

A integral imprópria converge.

Exemplo$\PageIndex{7}$: Integrating a Discontinuous Integrand

Avalie o$\displaystyle \int ^2_0x\ln x\,dx.$ estado se a integral converge ou diverge.

Solução

Como$f(x)=x\ln x$ é contínuo$(0,2]$ e descontínuo em zero, podemos reescrever a integral na forma de limite usando a Equação\ ref {improperundefa}:

\ (\ displaystyle\ begin {align*}\ int ^2_0x\ ln x\, dx &=\ lim_ {t→0^+}\ int ^2_tx\ ln x\, dx\ quad\ text {Reescrever como um limite.}\\ [4pt]
&=\ lim_ {t→0^+} (\ frac {1} {2} x^2\ ln x−\ frac {1} {4} x^2) ^2_t\ quad\ text {Evaluate}\;\ int x\ ln x\, dx\;\ text {usando integração por peças com}\; u=\ ln x\;\ text {e}\; dv=x. \\ [4pt]
&=\ lim_ {t→0^+} (2\ ln 2−1−\ frac {1} {2} t^2\ ln t+\ frac {1} {4} t^2). \ quad\ text {Avalie a antiderivada.}\\ [4pt]
&=2\ ln 2−1. \ quad\ text {Avalie o limite.} \ end {align*}\)

Portanto

$\displaystyle \lim_{t→0^+}t^2\ln t\;\text{is indeterminate.}$

Para avaliá-lo, reescreva como um quociente e aplique a regra de L'Hôpital.

A integral imprópria converge.

Exemplo$\PageIndex{8}$: Integrating a Discontinuous Integrand

$\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx.$Avalie se a integral imprópria converge ou diverge.

Solução

Como$f(x)=1/x^3$ é descontínuo em zero, usando a Equação\ ref {improperundefc}, podemos escrever

$$\int ^1_{−1}\frac{1}{x^3}\,dx=\int ^0_{−1}\frac{1}{x^3}\,dx+\int ^1_0\frac{1}{x^3}\,dx.\nonumber$$

Se uma das duas integrais divergir, a integral original diverge. Comece com$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$:

$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx=\lim_{t→0^−}\int ^t_{−1}\frac{1}{x^3}\,dx$Reescreva como limite.

$=\lim_{t→0^−}(−\frac{1}{2x^2})∣^t_{−1}$Encontre a antiderivada.

$=\lim_{t→0^−}(−\frac{1}{2t^2}+\frac{1}{2})$Avalie a antiderivada.

$=+∞.$Avalie o limite.

Portanto,$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$ diverge. Uma vez que$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$ diverge,$\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx$ diverge.

Exercício$\PageIndex{2}$

Avalie o$\displaystyle \int ^2_0\frac{1}{x}\,dx.$ estado se a integral converge ou diverge.

Dica

Escreva$\displaystyle \int ^2_0\frac{1}{x}\,dx$ em forma de limite usando a Equação\ ref {improperundefa}.

Resposta

$+∞$, Ele diverge.

Um teorema de comparação

Nem sempre é fácil ou mesmo possível avaliar diretamente uma integral imprópria; no entanto, comparando-a com outra integral cuidadosamente escolhida, pode ser possível determinar sua convergência ou divergência. Para ver isso, considere duas funções contínuas$f(x)$ e$g(x)$ satisfatórias$0≤f(x)≤g(x)$ para$x≥a$ (Figura$\PageIndex{6}$). Nesse caso, podemos ver integrais dessas funções em intervalos do formulário$[a,t]$ como áreas, então temos a relação

$$0≤\int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx \nonumber$$

para$t≥a$.

Figura$\PageIndex{6}$: Se for$0≤f(x)≤g(x)$ para$x≥a$, então para$t≥a$,$\displaystyle \int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx.$

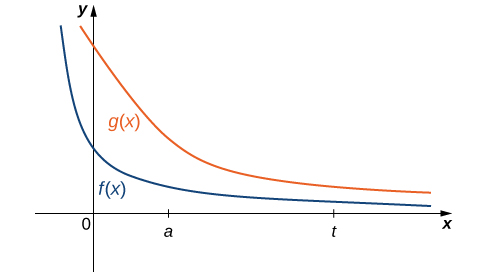
Assim, se

$$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber$$

depois

$$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞ \nonumber$$

também. Ou seja, se a área da região entre o gráfico de$f(x)$ e o$x$ eixo -acima$[a,+∞)$ for infinita, então a área da região entre o gráfico de$g(x)$ e o$x$ eixo -acima também$[a,+∞)$ é infinita.

Por outro lado, se

$$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L \nonumber$$

para algum número real$L$, então

$$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx \nonumber$$

deve convergir para algum valor menor ou igual a$L$, pois$\displaystyle \int ^t_af(x)\,dx$ aumenta à medida que$t$ aumenta e$\displaystyle \int ^t_af(x)\,dx≤L$ para todos$t≥a.$

Se a área da região entre o gráfico de$g(x)$ e o$x$ eixo -acima$[a,+∞)$ for finita, a área da região entre o gráfico de$f(x)$ e o$x$ eixo -acima também$[a,+∞)$ é finita.

Essas conclusões estão resumidas no seguinte teorema.

Um teorema de comparação

Deixe$f(x)$ e$g(x)$ seja contínuo.$[a,+∞).$ Suponha que$0≤f(x)≤g(x)$ para$x≥a.$

1. Se $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber$$ então $$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞. \nonumber$$
2. Se $$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L, \nonumber$$ onde$L$ está um número real, então $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=M \nonumber$$ para algum número real$M≤L.$

Exemplo$\PageIndex{9}$: Applying the Comparison Theorem

Use uma comparação para mostrar que

$$\int ^{+∞}_1\frac{1}{xe^x}\,dx \nonumber$$

converge.

Solução

Nós podemos ver isso

$$0≤\frac{1}{xe^x}≤\frac{1}{e^x}=e^{−x}, \nonumber$$

então, se$\displaystyle \int ^{+∞}_1e^{−x}\,dx$ converge, o mesmo acontece$\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx$. Para avaliar,$\displaystyle \int ^{+∞}_1e^{−x}\,dx,$ primeiro reescreva-o como um limite:

$\displaystyle \int ^{+∞}_1e^{−x}\,dx=\lim_{t→+∞}\int ^t_1e^{−x}\,dx$

$=\lim_{t→+∞}(−e^{−x})∣^t_1$

$=\lim_{t→+∞}(−e^{−t}+e^{-1})$

$=e^{-1}.$

Uma vez que$\displaystyle \int ^{+∞}_1e^{−x}\,dx$ converge, o mesmo acontece$\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx.$

Exemplo$\PageIndex{10}$: Applying the Comparison Theorem

Use o teorema da comparação para mostrar que$\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx$ diverge para todos$p<1$.

Solução

Para$p<1, 1/x≤1/(x^p)$ over$[1,+∞).$ In Example$\PageIndex{1}$, mostramos que$\displaystyle \int ^{+∞}_1\frac{1}{x}\,dx=+∞.$ Portanto,$\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx$ diverge para todos$p<1$.

Exercício$\PageIndex{3}$

Use uma comparação para mostrar que isso$\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx$ diverge.

Dica

$\frac{1}{x}≤\frac{\ln x}{x}$em$[e,+∞)$

Resposta

Uma vez que$\displaystyle \int ^{+∞}_e\frac{1}{x}\,dx=+∞,$$\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx$ diverge.

Transformações de Laplace

Nos últimos capítulos, analisamos várias maneiras de usar a integração para resolver problemas do mundo real. Para este próximo projeto, vamos explorar uma aplicação mais avançada da integração: transformações integrais. Especificamente, descrevemos a transformada de Laplace e algumas de suas propriedades. A transformada de Laplace é usada em engenharia e física para simplificar os cálculos necessários para resolver alguns problemas. Ele pega funções expressas em termos de tempo e as transforma em funções expressas em termos de frequência. Acontece que, em muitos casos, os cálculos necessários para resolver problemas no domínio da frequência são muito mais simples do que aqueles exigidos no domínio do tempo.

A transformação de Laplace é definida em termos de uma integral como

$$L{f(t)}=F(s)=\int ^∞_0e^{−st}f(t)dt. \nonumber$$

Observe que a entrada para uma transformada de Laplace é uma função do tempo$f(t),$ e a saída é uma função da frequência,$F(s)$. Embora muitos exemplos do mundo real exijam o uso de números complexos (envolvendo o número imaginário)$i=\sqrt{−1}),$ neste projeto, nos limitamos às funções de números reais.

Vamos começar com um exemplo simples. Aqui calculamos a transformação de Laplace de$f(t)=t$. Nós temos

$$L{t}=\int ^∞_0te^{−st}dt. \nonumber$$

Esta é uma integral imprópria, então a expressamos em termos de um limite, o que dá

$$L{t}=\int ^∞_0te^{−st}dt=\lim_{z→∞}\int ^z_0te^{−st}dt. \nonumber$$

Agora usamos a integração por partes para avaliar a integral. Observe que estamos integrando em relação a t, então tratamos a variável s como uma constante. Nós temos

$u=t$$du=dt$$dv=e^{−st}dt$$v=−\frac{1}{s}e^{−st}$.

Em seguida, obtemos

$$\begin{align*} \lim_{z→∞}\int ^z_0te^{−st}dt =\lim_{z→∞}[[−\frac{t}{s}e^{−st}]∣^z_0+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+\frac{0}{s}e^{−0s}]+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+0]−\frac{1}{s}[\frac{e^{−st}}{s}]∣^z_0] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}]−\frac{1}{s^2}[e^{−sz}−1]] \\[4pt]\ =\lim_{z→∞}[−\frac{z}{se^{sz}}]−\lim_{z→∞}[\frac{1}{s^2e^{sz}}]+\lim_{z→∞}\frac{1}{s^2} \\[4pt]\ =0−0+\frac{1}{s^2} \\[4pt]\ =\frac{1}{s^2}. \end{align*}$$

1. Calcule a transformação de Laplace de$f(t)=1.$
2. Calcule a transformação de Laplace de$f(t)=e^{−3t}.$
3. Calcule a transformação de Laplace de$f(t)=t^2$. (Observe que você precisará integrar por partes duas vezes.)

As transformadas de Laplace são frequentemente usadas para resolver equações diferenciais. As equações diferenciais não são abordadas em detalhes até mais tarde neste livro; mas, por enquanto, vamos examinar a relação entre a transformada de Laplace de uma função e a transformada de Laplace de sua derivada.

Vamos começar com a definição da transformação de Laplace. Nós temos

$$L{f(t)}=\int ^∞_0e^{−st}f(t)dt=\lim_{z→∞}\int ^z_0e^{−st}f(t)dt. \nonumber$$

Use a integração por peças para avaliar$\displaystyle \lim_{z→∞}\int ^z_0e^{−st}f(t)dt$. (Deixe$u=f(t)$$dv=e^{−st}dt$ e.)

Depois de integrar por peças e avaliar o limite, você deve ver que

$$L{f(t)}=\frac{f(0)}{s}+\frac{1}{s}[L{f′(t)}]. \nonumber$$

Então,

$$L{f′(t)}=sL{f(t)}−f(0). \nonumber$$

Assim, a diferenciação no domínio do tempo simplifica a multiplicação por s no domínio da frequência.

A última coisa que examinamos neste projeto é como as transformações de Laplace$f(t)$ e suas antiderivadas estão relacionadas. Deixe$g(t)=\int ^t_0f(u)du.$ então,

$$L{g(t)}=\int ^∞_0e^{−st}g(t)dt=\lim_{z→∞}\int ^z_0e^{−st}g(t)dt. \nonumber$$

Use a integração por peças para avaliar$\displaystyle \lim_{z→∞}\int ^z_0e^{−st}g(t)dt.$ (Let$u=g(t)$$dv=e^{−st}dt$ e. Observe, da maneira que definimos$g(t), du=f(t)dt.$)

Como você pode esperar, você deve ver que

$$L{g(t)}=\frac{1}{s}⋅L{f(t)}. \nonumber$$

A integração no domínio do tempo simplifica a divisão por$s$ no domínio da frequência.

Conceitos chave

• Integrais de funções em intervalos infinitos são definidas em termos de limites.
• Integrais de funções em um intervalo para o qual a função tem uma descontinuidade em um ponto final podem ser definidas em termos de limites.
• A convergência ou divergência de uma integral imprópria pode ser determinada comparando-a com o valor de uma integral imprópria pela qual a convergência ou divergência é conhecida.

Equações chave

• Integrais impróprios

$\displaystyle \int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx$

$\displaystyle \int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx$

$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx$

Glossário

integral impróprio

uma integral em um intervalo infinito ou uma integral de uma função contendo uma descontinuidade infinita no intervalo; uma integral imprópria é definida em termos de um limite. A integral imprópria converge se esse limite for um número real finito; caso contrário, a integral imprópria diverge