7.4E: Exercícios para a Seção 7.4

Last updated
Save as PDF

Page ID: 188319

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Use a decomposição parcial de frações (ou uma técnica mais simples) para expressar a função racional como uma soma ou diferença de duas ou mais expressões racionais mais simples.

1)\(\dfrac{1}{(x−3)(x−2)}\)

2)\(\dfrac{x^2+1}{x(x+1)(x+2)}\)

Resposta: \(\dfrac{x^2+1}{x(x+1)(x+2)} \quad = \quad −\dfrac{2}{x+1}+\dfrac{5}{2(x+2)}+\dfrac{1}{2x}\)

3)\(\dfrac{1}{x^3−x}\)

4)\(\dfrac{3x+1}{x^2}\)

Resposta: \(\dfrac{3x+1}{x^2} \quad = \quad \dfrac{1}{x^2}+\dfrac{3}{x}\)

5)\(\dfrac{3x^2}{x^2+1}\) (Dica: use a divisão longa primeiro.)

6)\(\dfrac{2x^4}{x^2−2x}\)

Resposta: \(\dfrac{2x^4}{x^2−2x} \quad = \quad 2x^2+4x+8+\dfrac{16}{x−2}\)

7)\(\dfrac{1}{(x−1)(x^2+1)}\)

8)\(\dfrac{1}{x^2(x−1)}\)

Resposta: \(\dfrac{1}{x^2(x−1)} \quad = \quad −\dfrac{1}{x^2}−\dfrac{1}{x}+\dfrac{1}{x−1}\)

9)\(\dfrac{x}{x^2−4}\)

10)\(\dfrac{1}{x(x−1)(x−2)(x−3)}\)

Resposta: \(\dfrac{1}{x(x−1)(x−2)(x−3)} \quad = \quad −\dfrac{1}{2(x−2)}+\dfrac{1}{2(x−1)}−\dfrac{1}{6x}+\dfrac{1}{6(x−3)}\)

11)\(\dfrac{1}{x^4−1}=\dfrac{1}{(x+1)(x−1)(x^2+1)}\)

12)\(\dfrac{3x^2}{x^3−1}=\dfrac{3x^2}{(x−1)(x^2+x+1)}\)

Resposta: \(\dfrac{3x^2}{x^3−1} \quad = \quad \dfrac{1}{x−1}+\dfrac{2x+1}{x^2+x+1}\)

13)\(\dfrac{2x}{(x+2)^2}\)

14)\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2}\)

Resposta: \(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2} \quad = \quad \dfrac{2}{x+1}+\dfrac{x}{x^2+4}−\dfrac{1}{(x^2+4)^2}\)

Nos exercícios 15 a 25, use o método de frações parciais para avaliar cada uma das seguintes integrais.

15)\(\displaystyle ∫\frac{dx}{(x−3)(x−2)}\)

16)\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx\)

Resposta: \(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx \quad = \quad 2\ln|x+4|+\ln|x-2|+C = \ln\left| (x+4)^2(x-2) \right| + C\)

17)\(\displaystyle ∫\frac{dx}{x^3−x}\)

18)\(\displaystyle ∫\frac{x}{x^2−4}\,dx\)

Resposta: Observe que você não precisa de frações parciais aqui. Usamos uma\(u\) substituição simples.
\(\displaystyle ∫\frac{x}{x^2−4}\,dx \quad = \quad \tfrac{1}{2}\ln|4−x^2|+C\)

19)\(\displaystyle ∫\frac{dx}{x(x−1)(x−2)(x−3)}\)

20)\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx\)

Resposta: Observe que, como o grau do numerador é igual ao grau do denominador, precisamos começar com uma divisão longa.
Em seguida, observe que precisaremos usar o preenchimento do quadrado para continuar, pois não podemos fatorar o trinômio no denominador.
\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx \quad = \quad 2\left(x+\tfrac{1}{3}\arctan\left(\frac{1+x}{3}\right)\right)+C\)

21)\(\displaystyle ∫\frac{dx}{x^2−5x+6}\)

22)\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx\)

Resposta: \(\displaystyle ∫\frac{2−x}{x^2+x}\,dx \quad = \quad 2\ln|x|−3\ln|1+x|+C = \ln\left| \frac{x^2}{(1+x)^3} \right|+C\)

23)\(\displaystyle ∫\frac{2}{x^2−x−6}\,dx\)

24)\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8}\)

Resposta: \(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8} \quad = \quad \tfrac{1}{16}\left(−\frac{4}{−2+x}−\ln|−2+x|+\ln|2+x|\right)+C = \tfrac{1}{16}\left(−\frac{4}{−2+x}+\ln\left| \frac{x+2}{x-2} \right|\right)+C\)

25)\(\displaystyle ∫\frac{dx}{x^4−10x^2+9}\)

Nos exercícios 26 a 29, avalie as integrais com fatores quadráticos irredutíveis nos denominadores.

26)\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx\)

Resposta: \(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx \quad = \quad \tfrac{1}{30}(−2\sqrt{5}\arctan\left[\frac{1+x}{\sqrt{5}}\right]+2\ln|−4+x|−\ln|6+2x+x^2|)+C\)

27)\(\displaystyle ∫\frac{x^2}{x^3−x^2+4x−4}\,dx\)

28)\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx\)

Resposta: Observe que precisamos usar a divisão longa primeiro, pois o grau do numerador é maior que o grau do denominador.
\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx \quad = \quad −\frac{3}{x}+4\ln|x+2|+x+C\)

29)\(\displaystyle ∫\frac{x}{(x−1)(x^2+2x+2)^2}\,dx\)

Nos exercícios 30 a 32, use o método das frações parciais para avaliar as integrais.

30)\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx\)

Resposta: \(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx \quad = \quad −\ln|3−x|+\tfrac{1}{2}\ln|x^2+4|+C\)

31)\(\displaystyle ∫\frac{2}{(x+2)^2(2−x)}\,dx\)

32)\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx\) (Dica: Use o teorema da raiz racional.)

Resposta: \(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx \quad = \quad \ln|x−2|−\tfrac{1}{2}\ln|x^2+2x+2|+C\)

Nos exercícios 33 a 46, use a substituição para converter as integrais em integrais de funções racionais. Em seguida, use frações parciais para avaliar as integrais.

33)\(\displaystyle ∫^1_0\frac{e^x}{36−e^{2x}}\,dx\) (Dê a resposta exata e o equivalente decimal. Arredonde para cinco casas decimais.)

34)\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx\)

Resposta: \(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx \quad = \quad −x+\ln|1−e^x|+C\)

(35)\(\displaystyle ∫\frac{\sin x\,dx}{1−\cos^2x}\)

36)\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx\)

Resposta: \(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx \quad = \quad \tfrac{1}{5}\ln\left|\frac{\cos x+3}{\cos x−2}\right|+C\)

37)\(\displaystyle ∫\frac{1−\sqrt{x}}{1+\sqrt{x}}\,dx\)

38)\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2}\)

Resposta: \(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2} \quad = \quad \frac{1}{2−2e^{2t}}+C\)

39)\(\displaystyle ∫\frac{1+e^x}{1−e^x}\,dx\)

40)\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}}\)

Resposta: \(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}} \quad = \quad 2\sqrt{1+x}−2\ln|1+\sqrt{1+x}|+C\)

41)\(\displaystyle ∫\frac{dx}{\sqrt{x}+\sqrt[4]{x}}\)

(42)\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx\)

Resposta: \(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx \quad = \quad \ln\left|\frac{\sin x}{1−\sin x}\right|+C\)

43)\(\displaystyle ∫\frac{e^x}{(e^{2x}−4)^2}\,dx\)

44)\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx\)

Resposta: \(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx \quad = \quad \frac{\sqrt{3}}{4}\)

45)\(\displaystyle ∫\frac{1}{2+e^{−x}}\,dx\)

(46)\(\displaystyle ∫\frac{1}{1+e^x}\,dx\)

Resposta: \(\displaystyle ∫\frac{1}{1+e^x}\,dx \quad = \quad x−\ln(1+e^x)+C\)

Nos exercícios 47 a 48, use a substituição dada para converter a integral em integral de uma função racional e, em seguida, calcule.

47)\(\displaystyle ∫\frac{1}{t−\sqrt[3]{t}}\,dt; \quad t=x^3\)

48)\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx; \quad x=u^6\)

Resposta: \(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx \quad = \quad 6x^{1/6}−3x^{1/3}+2\sqrt{x}−6\ln(1+x^{1/6})+C\)

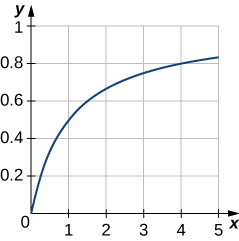
49) Faça um gráfico da curva\(y=\dfrac{x}{1+x}\) ao longo do intervalo\([0,5]\). Em seguida, encontre a área da região delimitada pela curva, pelo\(x\) eixo -e pela linha\(x=4\).

50) Encontre o volume do sólido gerado quando a região é delimitada\(y=\dfrac{1}{\sqrt{x(3−x)}}, \,y=0, \,x=1,\) e\(x=2\) é\(x\) girada em torno do eixo.

Resposta: \(V = \frac{4}{3}π\text{arctanh}\,\left[\frac{1}{3}\right]=\frac{1}{3}π\ln 4 \, \text{units}^3\)

51) A velocidade de uma partícula se movendo ao longo de uma linha é uma função do tempo dada por\(v(t)=\dfrac{88t^2}{t^2+1}.\) Encontre a distância que a partícula percorreu após\(t=5\) segundos.

Nos exercícios 52 a 54, resolva o problema do valor inicial de\(x\) em função de\(t\).

52)\((t^2−7t+12)\dfrac{dx}{dt}=1,\quad t>4,\, x(5)=0\)

Resposta: \( x=−\ln|t−3|+\ln|t−4|+\ln 2 = \ln\left| \dfrac{2(t-4)}{t-3}\right|\)

53)\((t+5)\dfrac{dx}{dt}=x^2+1, \quad t>−5,\,x(1)=\tan 1\)

54)\((2t^3−2t^2+t−1)\dfrac{dx}{dt}=3,\quad x(2)=0\)

Resposta: \(x=\ln|t−1|−\sqrt{2}\arctan(\sqrt{2}t)−\frac{1}{2}\ln(t^2+\frac{1}{2})+\sqrt{2}\arctan(2\sqrt{2})+\frac{1}{2}\ln 4.5\)

55) Encontre a\(x\) coordenada -do centróide da área delimitada por\(y(x^2−9)=1, \, y=0, \,x=4,\) e\(x=5.\) (arredonde a resposta para duas casas decimais.)

56) Encontre o volume gerado girando a área delimitada por\(y=\dfrac{1}{x^3+7x^2+6x},\, x=1,\, x=7\) e em\(y=0\) torno do\(y\) eixo.

Resposta: \(V = \frac{2}{5}π\ln\frac{28}{13} \, \text{units}^3\)

57) Encontre a área delimitada por\(y=\dfrac{x−12}{x^2−8x−20}, \,y=0, \,x=2,\)\(x=4\) e. (Arredonde a resposta para o centésimo mais próximo.)

58) Avalie a integral\(\displaystyle ∫\frac{dx}{x^3+1}.\)

Resposta: \(\displaystyle ∫\frac{dx}{x^3+1} \quad = \quad \frac{\arctan[\frac{−1+2x}{\sqrt{3}}]}{\sqrt{3}}+\frac{1}{3}\ln|1+x|−\frac{1}{6}\ln∣1−x+x^2∣+C\)

Para problemas 59 a 62, use as substituições\(\tan(\frac{x}{2})=t, \,dx=\dfrac{2}{1+t^2}\,dt, \, \sin x=\dfrac{2t}{1+t^2},\) e\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

(59)\(\displaystyle ∫\frac{dx}{3−5\sin x}\)

60) Encontre a área abaixo da curva\(y=\dfrac{1}{1+\sin x}\) entre\(x=0\) e\(x=π.\) (Suponha que as dimensões estejam em polegadas).

Resposta: 2,0 pol. ²

61) Dadas\(\tan\left(\frac{x}{2}\right)=t,\) derivam as fórmulas\(dx=\dfrac{2}{1+t^2}dt, \,\sin x=\dfrac{2t}{1+t^2}\), e\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

62) Avalie\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx.\)

Resposta: \(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx \quad = \quad 3(−8+x)^{1/3}−2\sqrt{3}\arctan\left[\frac{−1+(−8+x)^{1/3}}{\sqrt{3}}\right]−2\ln\left[2+(−8+x)^{1/3}\right]+\ln\left[4−2(−8+x)^{1/3}+(−8+x)^{2/3}\right]+C\)