7.3: Substituição trigonométrica

objetivos de aprendizagem

• Resolva problemas de integração envolvendo a raiz quadrada de uma soma ou diferença de dois quadrados.

Nesta seção, exploramos integrais contendo expressões da forma$\sqrt{a^2−x^2}$$\sqrt{a^2+x^2}$, e$\sqrt{x^2−a^2}$, onde os valores de$a$ são positivos. Já encontramos e avaliamos integrais contendo algumas expressões desse tipo, mas muitas ainda permanecem inacessíveis. A técnica de substituição trigonométrica é muito útil ao avaliar essas integrais. Essa técnica usa substituição para reescrever essas integrais como integrais trigonométricas.

Integrais envolvendo$\sqrt{a^2−x^2}$

Antes de desenvolver uma estratégia geral para integrais contendo$\sqrt{a^2−x^2}$, considere a integral.$\displaystyle ∫\textstyle\sqrt{9−x^2}dx.$ Essa integral não pode ser avaliada usando nenhuma das técnicas que discutimos até agora. No entanto, se fizermos a substituição$x=3\sin θ$, temos$dx=3\cos θ \, dθ.$ Depois de substituir na integral, temos

$$∫\sqrt{9−x^2}\,dx=∫\textstyle\sqrt{ 9−(3\sin θ)^2}\cdot 3\cos θ \,dθ. \nonumber$$

Depois de simplificar, temos

$$∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{1−\sin^2θ}\cdot\cos θ \, dθ. \nonumber$$

Deixando$1−\sin^2θ=\cos^2θ,$ que agora tenhamos

$$∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{\cos^2θ}\cos θ \, dθ. \nonumber$$

Supondo que$\cos θ≥0$, temos

$$∫\textstyle\sqrt{ 9−x^2}\,dx=∫ 9\cos^2θ \, dθ. \nonumber$$

Neste ponto, podemos avaliar a integral usando as técnicas desenvolvidas para integrar potências e produtos de funções trigonométricas. Antes de concluir este exemplo, vamos dar uma olhada na teoria geral por trás dessa ideia.

Para avaliar integrais envolvendo$\sqrt{a^2−x^2}$, fazemos a substituição$x=a\sin θ$$dx=a\cos θ$ e. Para ver se isso realmente faz sentido, considere o seguinte argumento: O domínio do$\sqrt{a^2−x^2}$ é$[−a,a]$. Assim,

$$−a≤x≤a. \nonumber$$

Consequentemente,

$$−1≤\dfrac{x}{a}≤1. \nonumber$$

Como o alcance de$\sin x$ mais$[−(π/2),π/2]$ é$[−1,1]$, há um ângulo único que$θ$ satisfaz$−(π/2)≤θ≤π/2$ isso$\sin θ=x/a$, ou equivalentemente, para que$x=a\sin θ$. Se substituirmos$x=a\sin θ$ em$\sqrt{a^2−x^2}$, obtemos

\ [\ begin {align*}\ sqrt {a^2−x^2} &=\ sqrt {a^2− (a\ sin θ) ^2} & &\ text {Let} x=a\ sin θ\ text {onde} −\ dfrac {π} {2} ≤θ≤\ dfrac {π} {2}.\\ [4pt]
& & &\ text {Simplifique.}\\ [4pt]
&=\ sqrt {a^2−a^2\ sin^2θ} & &\ text {Fator out} a^2.\\ [4pt]
&=\ sqrt {a^2 (1−\ sin^2θ)} & &\ text {Substitute} 1−\ sin^2x=\ cos^2x.\\ [4pt]
&=\ sqrt {a^2\ cos^2θ} & &\ text {Pegue a raiz quadrada.}\\ [4pt]
&=|a\ cos θ|\\ [4pt]
&=a\ cos θ\ end {align*}\]

Desde então$\cos x≥0$,$a>0, |a\cos θ|=a\cos θ.$ podemos ver, a partir desta discussão, que ao fazer a substituição$x=a\sin θ$, somos capazes de converter uma integral envolvendo um radical em uma integral envolvendo funções trigonométricas.$−\dfrac{π}{2}≤θ≤\dfrac{π}{2}$ Depois de avaliarmos a integral, podemos converter a solução novamente em uma expressão envolvendo$x$. Para ver como fazer isso, vamos começar assumindo que$0<x<a$. Nesse caso,$0<θ<\dfrac{π}{2}$. Uma vez que$\sin θ=\dfrac{x}{a}$, podemos desenhar o triângulo de referência na Figura$\PageIndex{1}$ para ajudar a expressar os valores$\cos θ, \, \tan θ,$ e as funções trigonométricas restantes em termos de x. Pode-se mostrar que esse triângulo realmente produz os valores corretos das funções trigonométricas avaliadas em$θ$ para todos os$θ$ satisfatórios$−\dfrac{π}{2}≤θ≤\dfrac{π}{2}$. É útil observar que a expressão$\sqrt{a^2−x^2}$ realmente aparece como o comprimento de um lado do triângulo. Por último, deve$θ$ aparecer por si só, usamos$θ=\sin^{−1}\left(\dfrac{x}{a}\right).$

Figura$\PageIndex{1}$: Um triângulo de referência pode ajudar a expressar as funções trigonométricas avaliadas$θ$ em termos de$x$.

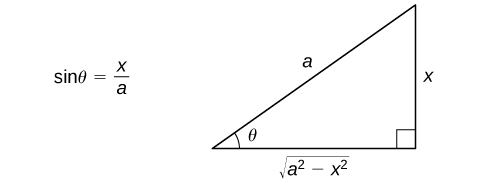
A parte essencial dessa discussão está resumida na seguinte estratégia de resolução de problemas.

Estratégia de resolução de problemas: integração de expressões envolvendo$\sqrt{a^2−x^2}$

1. É uma boa ideia garantir que a integral não possa ser avaliada facilmente de outra forma. Por exemplo, embora esse método possa ser aplicado a integrais do formulário$\displaystyle ∫\dfrac{1}{\sqrt{a^2−x^2}}dx$,$\displaystyle ∫\dfrac{x}{\sqrt{a^2−x^2}}dx,$ cada um$\displaystyle ∫x\sqrt{a^2−x^2}\,dx,$ deles possa ser integrado diretamente por fórmula ou por uma simples$u$ substituição.
2. Faça a substituição$x=a \sin θ$ e$dx=a\cos θ \,dθ.$ Nota: Esta substituição produz$\sqrt{a^2−x^2}=a\cos θ.$
3. Simplifique a expressão.
4. Avalie a integral usando técnicas da seção sobre integrais trigonométricas.
5. Use o triângulo de referência da Figura 1 para reescrever o resultado em termos de$x$. Você também pode precisar usar algumas identidades trigonométricas e a relação$θ=\sin^{−1}\left(\dfrac{x}{a}\right).$

O exemplo a seguir demonstra a aplicação dessa estratégia de solução de problemas.

Exemplo$\PageIndex{1}$: Integrating an Expression Involving $\sqrt{a^2−x^2}$

Avalie

$$∫\sqrt{ 9−x^2}dx. \nonumber$$

Solução

Comece fazendo as substituições$x=3\sin θ$ e$\sin θ=\dfrac{x}{3}$,$dx=3\cos θ \, dθ.$ desde então, podemos construir o triângulo de referência mostrado na Figura 2.

Figura$\PageIndex{2}$: Um triângulo de referência pode ser construído por exemplo$\PageIndex{1}$.

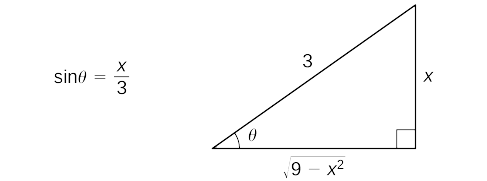
Assim,

$$∫\sqrt{9−x^2}\,dx=∫\sqrt{ 9−(3\sin θ)^2}3\cos θ\,dθ \nonumber$$

$x=3\sin θ$Substitua$dx=3\cos θ \,dθ$ e.

$=∫\sqrt{ 9(1−\sin^2θ)}\cdot 3\cos θ \, dθ$Simplifique.

$=∫\sqrt{ 9\cos^2θ}\cdot 3\cos θ \, dθ$Substituto$\cos^2θ=1−\sin^2θ$.

$=∫ 3|\cos θ|3\cos θ \, dθ$Pegue a raiz quadrada.

$=∫ 9\cos^2θ \, dθ$Simplifique. Desde$−\dfrac{π}{2}≤θ≤\dfrac{π}{2},\cos θ≥0$ e$|\cos θ|=\cos θ.$

$=∫ 9\left(\dfrac{1}{2}+\dfrac{1}{2}\cos(2θ)\right)\,dθ$Use a estratégia para integrar um poder uniforme do$\cos θ$.

$=\dfrac{9}{2}θ+\dfrac{9}{4}\sin(2θ)+C$Avalie a integral.

$=\dfrac{9}{2}θ+\dfrac{9}{4}(2\sin θ\cos θ)+C$

Substituto$\sin(2θ)=2\sin θ\cos θ$.

$=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{9}{2}⋅\dfrac{x}{3}⋅\dfrac{\sqrt{9−x^2}}{3}+C$$\sin^{−1}\left(\dfrac{x}{3}\right)=θ$Substitua$\sin θ=\frac{x}{3}$ e. Use o triângulo de referência para ver isso$\cos θ=\dfrac{\sqrt{9−x^2}}{3}$ e fazer essa substituição. Simplifique.

$=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{x\sqrt{9−x^2}}{2}+C.$Simplifique.

Exemplo$\PageIndex{2}$: Integrating an Expression Involving $\sqrt{a^2−x^2}$

Avalie

$$∫\dfrac{\sqrt{4−x^2}}{x}dx. \nonumber$$

Solução

Primeiro faça as substituições$x=2\sin θ$$dx=2\cos θ\,dθ$ e. Desde então$\sin θ=\dfrac{x}{2}$, podemos construir o triângulo de referência mostrado na Figura$\PageIndex{3}$.

Figura$\PageIndex{3}$: Um triângulo de referência pode ser construído por exemplo$\PageIndex{2}$.

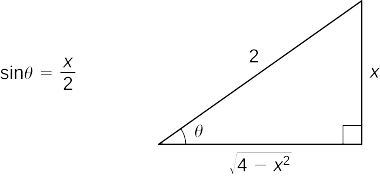
Assim,

$∫\dfrac{\sqrt{4−x^2}}{x}dx=∫\dfrac{\sqrt{4−(2\sin θ)^2}}{2\sin θ}2\cos θ \, dθ$Substituir$x=2\sin θ$ e$dx=2\cos θ\,dθ.$

$=∫\dfrac{2\cos^2θ}{\sin θ}\,dθ$Substitua$\cos^2θ=1−\sin^2θ$ e simplifique.

$=∫\dfrac{2(1−\sin^2θ)}{\sin θ}\,dθ$Substituto$\cos^2θ=1−\sin^2θ$.

$=∫ (2\csc θ−2\sin θ)\,dθ$Separe o numerador, simplifique e use$\csc θ=\dfrac{1}{\sin θ}$.

$=2 \ln |\csc θ−\cot θ|+2\cos θ+C$Avalie a integral.

$=2 \ln \left|\dfrac{2}{x}−\dfrac{\sqrt{4−x^2}}{x}\right|+\sqrt{4−x^2}+C.$Use o triângulo de referência para reescrever a expressão em termos de$x$ e simplificar.

No exemplo a seguir, vemos que às vezes temos uma escolha de métodos.

Exemplo$\PageIndex{3}$: Integrating an Expression Involving $\sqrt{a^2−x^2}$ Two Ways

Avalie$∫ x^3\sqrt{1−x^2}dx$ duas maneiras: primeiro usando a substituição$u=1−x^2$ e depois usando uma substituição trigonométrica.

Método 1

Deixe$u=1−x^2$ e daí$x^2=1−u$. Assim,$du=−2x\,dx.$ neste caso, a integral se torna

$∫ x^3\sqrt{1−x^2}\,dx=−\dfrac{1}{2}∫ x^2\sqrt{1−x^2}(−2x\,dx)$Faça a substituição.

$=−\dfrac{1}{2}∫ (1−u)\sqrt{u}\,du$Expanda a expressão.

$=−\dfrac{1}{2}∫(u^{1/2}−u^{3/2})\,du$Avalie a integral.

$=−\dfrac{1}{2}(\dfrac{2}{3}u^{3/2}−\dfrac{2}{5}u^{5/2})+C$Reescreva em termos de x.

$=−\dfrac{1}{3}(1−x^2)^{3/2}+\dfrac{1}{5}(1−x^2)^{5/2}+C.$

Método 2

Deixe$x=\sin θ$. Nesse caso,$dx=\cos θ \, dθ.$ usando essa substituição, temos

$∫ x^3\sqrt{1−x^2}dx=∫ \sin^3θ\cos^2θ \, dθ$

$=∫ (1−\cos^2θ)\cos^2θ\sin θ \, dθ$Deixe$u=\cos θ$. Assim,$du=−\sin θ \, dθ.$

$=∫ (u^4−u^2)\,du$

$=\dfrac{1}{5}u^5−\dfrac{1}{3}u^3+C$Substituto$\cos θ=u.$

$=\dfrac{1}{5}\cos^5θ−\dfrac{1}{3}\cos^3θ+C$Use um triângulo de referência para ver isso$\cos θ=\sqrt{1−x^2}.$

$=\dfrac{1}{5}(1−x^2)^{5/2}−\dfrac{1}{3}(1−x^2)^{3/2}+C.$

Exercício$\PageIndex{1}$

Reescreva a integral$\displaystyle ∫\dfrac{x^3}{\sqrt{25−x^2}}\,dx$ usando a substituição trigonométrica apropriada (não avalie a integral).

Dica

Substituir$x=5\sin θ$ e$dx=5\cos θ \, dθ.$

Responda

$\displaystyle ∫ 125\sin^3θ \, dθ$

Integrando expressões envolvendo$\sqrt{a^2+x^2}$

Para integrais contendo$\sqrt{a^2+x^2}$, vamos primeiro considerar o domínio dessa expressão. Como$\sqrt{a^2+x^2}$ é definido para todos os valores reais de$x$, restringimos nossa escolha às funções trigonométricas que têm um intervalo de todos os números reais. Portanto, nossa escolha se restringe à seleção de um$x=a\tan θ$ ou$x=a\cot θ$. Qualquer uma dessas substituições realmente funcionaria, mas a substituição padrão é$x=a\tan θ$ ou, equivalentemente,$\tan θ=x/a$. Com essa substituição, assumimos que$−(π/2)<θ<π/2$, para que também tenhamos.$θ=\tan^{−1}(x/a).$ O procedimento para usar essa substituição está descrito na seguinte estratégia de resolução de problemas.

Estratégia de resolução de problemas: integração de expressões envolvendo$\sqrt{a^2+x^2}$

1. Verifique se a integral pode ser avaliada facilmente usando outro método. Em alguns casos, é mais conveniente usar um método alternativo.
2. Substituir$x=a\tan θ$ e$dx=a\sec^2θ \, dθ.$ Esta substituição produz$\sqrt{a^2+x^2}=\sqrt{a^2+(a\tan θ)^2}=\sqrt{a^2(1+\tan^2θ)}=\sqrt{a^2sec^2θ}=|a\sec θ|=a\sec θ.$ (Desde$−\dfrac{π}{2}<θ<\dfrac{π}{2}$ e$\sec θ>0$ ao longo desse intervalo,$|a\sec θ|=a\sec θ$.)
3. Simplifique a expressão.
4. Avalie a integral usando técnicas da seção sobre integrais trigonométricas.
5. Use o triângulo de referência da Figura$\PageIndex{4}$ para reescrever o resultado em termos de$x$. Você também pode precisar usar algumas identidades trigonométricas e o relacionamento$θ=\tan^{−1}\left(\dfrac{x}{a}\right)$. (Nota: O triângulo de referência é baseado na suposição de que$x>0$; no entanto, as razões trigonométricas produzidas a partir do triângulo de referência são as mesmas das quais$x≤0$.)

Figura$\PageIndex{4}$: Um triângulo de referência pode ser construído para expressar as funções trigonométricas avaliadas$θ$ em termos de$x$.

Exemplo$\PageIndex{4}$: Integrating an Expression Involving $\sqrt{a^2+x^2}$

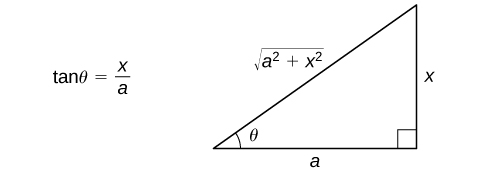
Avalie$\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}$ e verifique a solução por meio da diferenciação.

Solução

Comece com a substituição$x=\tan θ$$dx=sec^2θ\,dθ$ e. Desde então$\tan θ=x$, desenhe o triângulo de referência na Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$: O triângulo de referência, por exemplo$\PageIndex{4}$.

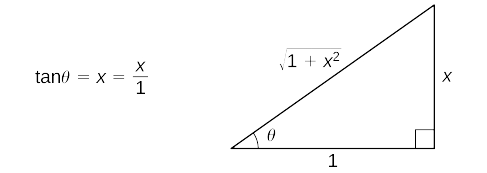
Assim,

\ (\ displaystyle\ begin {align*} ∫\ dfrac {dx} {\ sqrt {1+x^2}} &=∫\ dfrac {\ sec^2θ} {\ sec θ} dθ & &\ text {Substitute} x=\ tan θ\ text {e} dx=\ sec^2θ\, dθ.\\ [4pt]
& &\ texto {Esta substituição faz com que}\ sqrt {1+x^2} =\ sec θ. \ text {Simplifique.}\\ [4pt]
&=∫\ sec θ\, dθ & &\ text {Avalie a integral.}\\ [4pt]
&=\ ln |\ sec θ+\ tan θ|+C & &\ text {Use o triângulo de referência para expressar o resultado em termos de} x.\\ [4pt]
&=\ ln |\ sqrt {1+x^2} +x|+c\ end {align*}\)

Para verificar a solução, diferencie:

$\dfrac{d}{dx}\Big( \ln |\sqrt{1+x^2}+x|\Big)=\dfrac{1}{\sqrt{1+x^2}+x}⋅\left(\dfrac{x}{\sqrt{1+x^2}}+1\right) =\dfrac{1}{\sqrt{1+x^2}+x}⋅\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\dfrac{1}{\sqrt{1+x^2}}.$

Já que$\sqrt{1+x^2}+x>0$ para todos os valores de$x$, poderíamos reescrever$\ln |\sqrt{1+x^2}+x|+C= \ln (\sqrt{1+x^2}+x)+C$, se quiséssemos.

Exemplo$\PageIndex{5}$: Evaluating $∫\dfrac{dx}{\sqrt{1+x^2}}$ Using a Different Substitution

Use a substituição$x=\sinh θ$ para avaliar$\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}.$

Solução

Porque$\sinh θ$ tem um intervalo de todos os números reais$1+\sinh^2θ=\cosh^2θ$, e também podemos usar a substituição$x=\sinh θ$ para calcular essa integral. Nesse caso,$dx=\cosh θ \,dθ.$ Consequentemente,

\ (\ displaystyle\ begin {align*} ∫\ dfrac {dx} {\ sqrt {1+x^2}} &=∫\ dfrac {\ cosh θ} {\ sqrt {1+\ sinh^2θ}} dθ & &\ text {Substitute} x=\ sinh θ\ text {e} dx=\ cosh θ\, dθ\.\ [4pt]
& & &\ texto {Substituto} 1+\ sinh^2θ=\ cosh^2θ.\\ [4pt]
&=∫\ dfrac {\ cosh θ} {\ sqrt {\ cosh^2θ}} dθ & amp; &\ text {Desde}\ sqrt {\ cosh^2θ} =|\ cosh θ|\\ [4pt]
&=∫\ dfrac {\ cosh θ} {|\ cosh θ|} dθ & & |\ cosh θ|=\ cosh θ\ text {since}\ cosh θ>0\ texto {para todos} θ.\\ [4pt]
∫\ dfrac {\ cosh θ} {\ cosh θ} dθ & &\ text {Simplifique.}\\ [4pt]
&=∫ 1\, dθ & & \ text {Calcule a integral.}\\ [4pt]
&=θ+C & &\ text {Desde} x=\ sinh θ,\ text {nós sabemos} θ=\ sinh^ {−1} x.\ [4pt]
&=\ sinh^ {−1} x+C.\ end {align*}\)

Análise

Essa resposta parece bem diferente da resposta obtida usando a substituição.$x=\tan θ.$ Para ver se as soluções são as mesmas, defina$y=\sinh^{−1}x$. Assim,$\sinh y=x.$ a partir dessa equação, obtemos:

$$\dfrac{e^y−e^{−y}}{2}=x. \nonumber$$

Depois de multiplicar os dois lados$2e^y$ e reescrever, essa equação se torna:

$$e^{2y}−2xe^y−1=0. \nonumber$$

Use a equação quadrática para resolver$e^y$:

$$e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}. \nonumber$$

Simplificando, temos:

$$e^y=x±\sqrt{x^2+1}. \nonumber$$

Desde então$x−\sqrt{x^2+1}<0$, deve ser o caso de$e^y=x+\sqrt{x^2+1}$. Assim,

$$y= \ln (x+\sqrt{x^2+1}). \nonumber$$

Por último, obtemos

$$\sinh^{−1}x= \ln (x+\sqrt{x^2+1}). \nonumber$$

Depois de fazermos a observação final de que, desde$x+\sqrt{x^2+1}>0,$

$$\ln (x+\sqrt{x^2+1})= \ln ∣\sqrt{1+x^2}+x∣, \nonumber$$

vemos que os dois métodos diferentes produziram soluções equivalentes.

Exemplo$\PageIndex{6}$: Finding an Arc Length

Encontre o comprimento da curva$y=x^2$ ao longo do intervalo$[0,\dfrac{1}{2}]$.

Solução

Porque$\dfrac{dy}{dx}=2x$, o comprimento do arco é dado por

$$∫^{1/2}_0\sqrt{1+(2x)^2}dx=∫^{1/2}_0\sqrt{1+4x^2}dx. \nonumber$$

Para avaliar essa integral, use a substituição$x=\dfrac{1}{2}\tan θ$$dx=\tfrac{1}{2}\sec^2θ \, dθ$ e. Também precisamos mudar os limites da integração. Se$x=0$, então$θ=0$ e se$x=\dfrac{1}{2}$, então$θ=\dfrac{π}{4}.$ Assim,

$∫^{1/2}_0\sqrt{1+4x^2}dx=∫^{π/4}_0\sqrt{1+\tan^2θ}\cdot \tfrac{1}{2}\sec^2θ \, dθ$Após a substituição,$\sqrt{1+4x^2}=\sec θ$. (Substitua$1+\tan^2θ=\sec^2θ$ e simplifique.)

$=\tfrac{1}{2}∫^{π/4}_0\sec^3θ \, dθ$Derivamos essa integral na seção anterior.

$=\tfrac{1}{2}(\dfrac{1}{2}\sec θ\tan θ+ \dfrac{1}{2}\ln |\sec θ+\tan θ|)∣^{π/4}_0$Avalie e simplifique.

$=\tfrac{1}{4}(\sqrt{2}+ \ln (\sqrt{2}+1)).$

Exercício$\PageIndex{2}$

Reescreva$\displaystyle ∫ x^3\sqrt{x^2+4}dx$ usando uma substituição envolvendo$\tan θ$.

Dica

Use$x=2\tan θ$ e$dx=2\sec^2θ \, dθ.$

Responda

$$∫ 32\tan^3θ\sec^3θ \, dθ \nonumber$$

Integrando expressões envolvendo$\sqrt{x^2−a^2}$

O domínio da expressão$\sqrt{x^2−a^2}$ é$(−∞,−a]∪[a,+∞)$. Assim,$x\le −a$ ou$x\ge a.$ portanto,$\dfrac{x}{a}≤−1$ ou$\dfrac{x}{a}≥1$. Como esses intervalos correspondem ao intervalo de$\sec θ$ no conjunto$[0,\dfrac{π}{2})∪(\dfrac{π}{2},π]$, faz sentido usar a substituição$\sec θ=\dfrac{x}{a}$ ou, equivalentemente$x=a\sec θ$, onde$0≤θ<\dfrac{π}{2}$ ou$\dfrac{π}{2}<θ≤π$. A substituição correspondente para$dx$ é$dx=a\sec θ\tan θ \, dθ$. O procedimento para usar essa substituição é descrito na seguinte estratégia de resolução de problemas.

Estratégia de resolução de problemas: integrais envolvendo$\sqrt{x^2−a^2}$

1. Verifique se a integral não pode ser avaliada usando outro método. Nesse caso, podemos considerar a aplicação de uma técnica alternativa.
2. $x=a\sec θ$Substitua$dx=a\sec θ\tan θ \, dθ$ e. Essa substituição gera $$\sqrt{x^2−a^2}=\sqrt{(a\sec θ)^2−a^2}=\sqrt{a^2(\sec^2θ-1)}=\sqrt{a^2\tan^2θ}=|a\tan θ|. \nonumber$$ Para$x≥a, |a\tan θ|=a\tan θ$ e para$x≤−a, |a\tan θ|=−a\tan θ.$
3. Simplifique a expressão.
4. Avalie a integral usando técnicas da seção sobre integrais trigonométricas.
5. Use os triângulos de referência da Figura$\PageIndex{6}$ para reescrever o resultado em termos de$x$.
6. Você também pode precisar usar algumas identidades trigonométricas e o relacionamento$θ=\sec^{−1}\left(\dfrac{x}{a}\right)$. (Nota: Precisamos dos dois triângulos de referência, pois os valores de algumas das razões trigonométricas são diferentes dependendo se$x>a$ ou não$x<−a$.)

a. Há também as equações sin (teta) = a raiz quadrada de (x^2-a^2) /x, cos (teta) = a/x e tan (teta) = a raiz quadrada de (x^2-a^2) /a. O segundo triângulo está no segundo quadrante, com a hipotenusa rotulada —x. A perna horizontal é rotulado como —a e está no eixo x negativo. A perna vertical é chamada de raiz quadrada de (x^2-a^2). À direita do triângulo está a equação sec (theta) = x/a, x<-a. Há também as equações sin (theta) = a raiz quadrada negativa de (x^2-a^2) /x, cos (theta) = a/x e tan (teta) = a raiz quadrada negativa de (x^2-a^2) /a." src="https://math.libretexts.org/@api/dek...2447/7.3.4.png">

Figura$\PageIndex{6}$: Use o triângulo de referência apropriado para expressar as funções trigonométricas avaliadas$θ$ em termos de$x$.

Exemplo$\PageIndex{7}$: Finding the Area of a Region

Encontre a área da região entre o gráfico de$f(x)=\sqrt{x^2−9}$ e o eixo x ao longo do intervalo$[3,5].$

Solução

Primeiro, esboce um gráfico aproximado da região descrita no problema, conforme mostrado na figura a seguir.

Figura$\PageIndex{7}$: O cálculo da área da região sombreada requer a avaliação de uma integral com uma substituição trigonométrica.

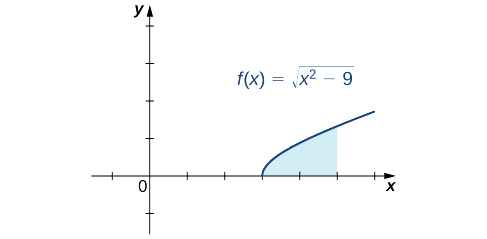
Podemos ver que a área é$A=∫^5_3\sqrt{x^2−9}dx$. Para avaliar essa integral definida, substitua$x=3\sec θ$$dx=3\sec θ\tan θ \, dθ$ e. Devemos também mudar os limites da integração. Se$x=3$, então$3=3\sec θ$ e daí em diante$θ=0$. Se$x=5$, então$θ=\sec^{−1}(\dfrac{5}{3})$. Depois de fazer essas substituições e simplificar, temos

Área$=∫^5_3\sqrt{x^2−9}dx$

$=∫^{\sec^{−1}(5/3)}_09\tan^2θ\sec θ \, dθ$Use$\tan^2θ=\sec^2θ - 1.$

$=∫^{\sec^{−1}(5/3)}_09(\sec^2θ−1)\sec θ \, dθ$Expandir.

$=∫^{\sec^{−1}(5/3)}_09(\sec^3θ−\sec θ)\,dθ$Avalie a integral.

$=(\dfrac{9}{2} \ln |\sec θ+\tan θ|+\dfrac{9}{2}\sec θ\tan θ)−9 \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0$Simplifique.

$=\dfrac{9}{2}\sec θ\tan θ−\dfrac{9}{2} \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0$Avalie. Use$\sec(\sec^{−1}\dfrac{5}{3})=\dfrac{5}{3}$ e$\tan(\sec^{−1}\dfrac{5}{3})=\dfrac{4}{3}.$

$=\dfrac{9}{2}⋅\dfrac{5}{3}⋅\dfrac{4}{3}−\dfrac{9}{2} \ln ∣\dfrac{5}{3}+\dfrac{4}{3}∣−(\dfrac{9}{2}⋅1⋅0−\dfrac{9}{2} \ln |1+0|)$

$=10−\dfrac{9}{2} \ln 3$

Exercício$\PageIndex{3}$

Avaliar $$∫\dfrac{dx}{\sqrt{x^2−4}}. \nonumber$$ Suponha que$x>2.$

Dica

Substituir$x=2\sec θ$ e$dx=2\sec θ\tan θ \, dθ.$

Responda

$$\ln |\dfrac{x}{2}+\dfrac{\sqrt{x^2−4}}{2}|+C \nonumber$$

Conceitos-chave

• Para integrais envolvendo$\sqrt{a^2−x^2}$, use a substituição$x=a\sin θ$ e$dx=a\cos θ \, dθ.$
• Para integrais envolvendo$\sqrt{a^2+x^2}$, use a substituição$x=a\tan θ$$dx=a\sec^2θ \, dθ$ e.
• Para integrais envolvendo$\sqrt{x^2−a^2}$, substitua$x=a\sec θ$$dx=a\sec θ\tan θ \,dθ$ e.

Glossário

substituição trigonométrica

uma técnica de integração que converte uma integral algébrica contendo expressões da forma$\sqrt{a^2−x^2}$$\sqrt{a^2+x^2}$, ou$\sqrt{x^2−a^2}$ em uma integral trigonométrica