7.1: Integração por peças
- Page ID
- 188282
- Saiba quando usar a integração por partes.
- Use a fórmula de integração por peças para resolver problemas de integração.
- Use a fórmula de integração por partes para integrais definidas.
Até agora, temos um procedimento bastante completo para avaliar muitos integrais básicos. No entanto, embora possamos integrar\(∫x \sin (x^2)\,dx\) usando a substituição\(u=x^2\), algo tão simples quanto nos\(∫x\sin x\,\,dx\) desafia. Muitos estudantes querem saber se existe uma regra de produto para integração. Não existe, mas existe uma técnica baseada na regra de diferenciação do produto que nos permite trocar uma integral por outra. Chamamos essa técnica de integração por partes.
A fórmula de integração por peças
Se, então\(h(x)=f(x)g(x)\), usando a regra do produto, obtivermos
\[h′(x)=f′(x)g(x)+g′(x)f(x). \label{eq1} \]
Embora à primeira vista possa parecer contraproducente, vamos agora integrar os dois lados da Equação\ ref {eq1}:
\[∫h′(x)\,\,dx=∫(g(x)f′(x)+f(x)g′(x))\,\,dx. \nonumber \]
Isso nos dá
\[ h(x)=f(x)g(x)=∫g(x)f′(x)\,dx+∫f(x)g′(x)\,\,dx. \nonumber \]
Agora resolvemos para\(∫f(x)g′(x)\,\,dx:\)
\[ ∫f(x)g′(x)\,dx=f(x)g(x)−∫g(x)f′(x)\,\,dx. \nonumber \]
Ao fazer as substituições\(u=f(x)\) e\(v=g(x)\), que por sua vez fazem\(du=f′(x)\,dx\) e\(dv=g′(x)\,dx\), temos a forma mais compacta
\[ ∫u\,dv=uv−∫v\,du. \nonumber \]
Funções let\(u=f(x)\) and\(v=g(x)\) be com derivadas contínuas. Então, a fórmula de integração por partes para a integral envolvendo essas duas funções é:
\[∫u\,dv=uv−∫v\,du. \label{IBP} \]
A vantagem de usar a fórmula de integração por partes é que podemos usá-la para trocar uma integral por outra, possivelmente mais fácil. O exemplo a seguir ilustra seu uso.
Use a integração por peças com\(u=x\) e\(dv=\sin x\,\,dx\) para avaliar
\[∫x\sin x\,\,dx. \nonumber \]
Solução
Ao escolher\(u=x\), nós temos\(du=1\,\,dx\). Desde então\(dv=\sin x\,\,dx\), obtemos
\[v=∫\sin x\,\,dx=−\cos x. \nonumber \]
É útil acompanhar esses valores da seguinte forma:
- \(u=x\)
- \(dv=\sin x\,\,dx\)
- \(du=1\,dx\)
- \(v=∫\sin x\,\,dx=−\cos x.\)
A aplicação da fórmula de integração por peças (Equação\ ref {IBP}) resulta em
\[ \begin{align} ∫x\sin x\,\,dx &=(x)(−\cos x)−∫(−\cos x)(1\,\,dx) \tag{Substitute} \\[4pt] &=−x\cos x+∫\cos x\,\,dx \tag{Simplify} \end{align} \]
Em seguida, use
\[∫\cos x\,\,dx =\sin x+C. \nonumber \]
para obter
\[∫x\sin x\,\,dx =−x\cos x+\sin x+C. \nonumber \]
Análise
Neste ponto, provavelmente existem alguns itens que precisam de esclarecimentos. Em primeiro lugar, você pode estar curioso sobre o que teria acontecido se tivéssemos escolhido\(u=\sin x\)\(dv=x\) e. Se tivéssemos feito isso, então teríamos\(du=\cos x\)\(v=\dfrac{1}{2}x^2\) e. Assim, após aplicar a integração por peças (Equação\ ref {IBP}), temos
\[ ∫x\sin x\,\,dx=\dfrac{1}{2}x^2\sin x−∫\dfrac{1}{2}x^2\cos x\,\,dx. \nonumber \]
Infelizmente, com a nova integral, não estamos em uma posição melhor do que antes. É importante ter em mente que, quando aplicamos a integração por partes, talvez precisemos tentar várias opções para\(u\) e\(dv\) antes de encontrar uma opção que funcione.
Segundo, você pode se perguntar por que\(v=∫\sin x\,\,dx=−\cos x\), quando descobrimos, não usamos.\(v=−\cos x+K.\) Para ver que não faz diferença, podemos retrabalhar o problema usando\(v=−\cos x+K\):
\[ \begin{align*} ∫x\sin x\,\,dx &=(x)(−\cos x+K)−∫(−\cos x+K)(1\,\,dx) \\[4pt] &=−x\cos x+Kx+∫\cos x\,\,dx−∫K\,\,dx \\[4pt] &=−x\cos x+Kx+\sin x−Kx+C \\[4pt] &=−x\cos x+\sin x+C. \end{align*}\]
Como você pode ver, não faz diferença na solução final.
Por fim, podemos verificar se nossa antiderivada está correta, diferenciando\(−x\cos x+\sin x+C:\)
\[ \begin{align*} \dfrac{d}{\,dx}(−x\cos x+\sin x+C) = \cancel{(−1)\cos x} + (−x)(−\sin x) + \cancel{\cos x} \\[4pt] =x\sin x \end{align*}\]
Portanto, o antiderivado é verificado.
Avalie\(∫xe^{2x}\,dx\) usando a fórmula de integração por partes (Equação\ ref {IBP}) com\(u=x\)\(dv=e^{2x}\,\,dx\) e.
- Dica
-
Encontre\(du\) e\(v\) e use o exemplo anterior como guia.
- Resposta
-
\[ ∫xe^{2x}\,\,dx=\dfrac{1}{2}xe^{2x}−\dfrac{1}{4}e^{2x}+C \nonumber \]
A pergunta natural a ser feita neste momento é: Como sabemos escolher\(u\) e\(dv\)? Às vezes, é uma questão de tentativa e erro; no entanto, a sigla LIATE muitas vezes pode ajudar a eliminar algumas das suposições de nossas escolhas. Este acrônimo significa Funções Logarítmicas L, Funções Trigonométricas Inversas, Funções Algébricas A, Funções Trigonométricas e Funções Exponenciais E. Esse mnemônico serve como uma ajuda na determinação de uma escolha apropriada para\(u\). O tipo de função na integral que aparece primeiro na lista deve ser nossa primeira escolha de\(u\).
Por exemplo, se uma integral contém uma função logarítmica e uma função algébrica, devemos escolher ser\(u\) a função logarítmica, porque L vem antes de A em LIATE. A integral em Example\(\PageIndex{1}\) tem uma função trigonométrica (\(\sin x\)) e uma função algébrica (\(x\)). Como A vem antes de T em LIATE, escolhemos ser\(u\) a função algébrica. Quando escolhemos\(u\),\(dv\) é selecionado para ser a parte restante da função a ser integrada, junto com\(\,dx\).
Por que esse mnemônico funciona? Lembre-se de que tudo o que escolhermos ser\(dv\) deve ser algo que possamos integrar. Como não temos fórmulas de integração que nos permitam integrar funções logarítmicas simples e funções trigonométricas inversas, faz sentido que elas não sejam escolhidas como valores para\(dv\). Consequentemente, eles devem estar no topo da lista como opções para\(u\). Assim, colocamos LI no início do mnemônico. (Poderíamos facilmente ter começado com o IL, já que esses dois tipos de funções não aparecerão juntos em um problema de integração por partes.) As funções exponenciais e trigonométricas estão no final da nossa lista porque são bastante fáceis de integrar e para as quais fazem boas escolhas\(dv\). Assim, temos TE no final do nosso mnemônico. (Poderíamos facilmente ter usado o ET no final, pois quando esses tipos de funções aparecem juntos, geralmente não importa qual é\(u\) e qual é\(dv\).) As funções algébricas geralmente são fáceis de integrar e diferenciar, e elas vêm no meio do mnemônico.
Avalie\[∫\dfrac{\ln x}{x^3}\,\,dx. \nonumber \]
Solução
Comece reescrevendo a integral:
\[∫\dfrac{\ln x}{x^3}\,\,dx=∫x^{−3}\ln x\,\,dx. \nonumber \]
Como essa integral contém a função algébrica\(x^{−3}\) e a função logarítmica\(\ln x\), escolha\(u=\ln x\), já que\(L\) vem antes de A em LIATE. Depois de escolhermos\(u=\ln x\), devemos escolher\(dv=x^{−3}\,dx\).
Em seguida, já que\(u=\ln x,\) temos\(du=\dfrac{1}{x}\,dx.\) também,\(v=∫x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.\) resumindo,
- \(u=\ln x\)
- \(du=\dfrac{1}{x}\,dx\)
- \(dv=x^{−3}\,dx\)
- \(v=∫x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.\)
Substituindo na fórmula de integração por partes (Equação\ ref {IBP}) fornece
\[ \begin{align*} ∫\dfrac{\ln x}{x^3}\,dx &=∫x^{−3}\ln x\,dx=(\ln x)(−\dfrac{1}{2}x^{−2})−∫(−\dfrac{1}{2}x^{−2})(\dfrac{1}{x}\,dx) \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x+∫\dfrac{1}{2}x^{−3}\,\,dx \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x−\dfrac{1}{4}x^{−2}+C\ \\[4pt] &=−\dfrac{1}{2x^2}\ln x−\dfrac{1}{4x^2}+C \end{align*} \nonumber \]
Avalie\[∫x\ln x \,\,dx. \nonumber \]
- Dica
-
Use\(u=\ln x\)\(dv=x\,\,dx\) e.
- Resposta
-
\[∫x\ln x \,\,dx=\dfrac{1}{2}x^2\ln x−\dfrac{1}{4}x^2+C \nonumber \]
Em alguns casos, como nos próximos dois exemplos, pode ser necessário aplicar a integração por partes mais de uma vez.
Avalie\[∫x^2e^{3x}\,dx. \nonumber \]
Solução
Usando LIATE, escolha\(u=x^2\)\(dv=e^{3x}\,dx\) e. Assim,\(du=2x\,dx\)\(v=∫e^{3x}\,dx=\left(\dfrac{1}{3}\right)e^{3x}\) e. Portanto,
- \(u=x^2\)
- \(du=2x\,dx\)
- \(dv=e^{3x}\,dx\)
- \(v=∫e^{3x}\,dx=\dfrac{1}{3}e^{3x}.\)
Substituir na Equação\ ref {IBP} produz
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−∫\dfrac{2}{3}xe^{3x}\,dx. \label{3A.2} \]
Ainda não podemos integrar\(∫\dfrac{2}{3}xe^{3x}\,dx\) diretamente, mas a integral agora tem uma potência menor ligada\(x\). Podemos avaliar essa nova integral usando a integração por partes novamente. Para fazer isso, escolha
\[u=x \nonumber \]
e
\[dv=\dfrac{2}{3}e^{3x}\,dx. \nonumber \]
Assim,
\[du=\,dx \nonumber \]
e
\[v=∫\left(\dfrac{2}{3}\right)e^{3x}\,dx=\left(\dfrac{2}{9}\right)e^{3x}. \nonumber \]
Agora temos
- \(u=x\)
- \(du=\,dx\)
- \(dv=\dfrac{2}{3}e^{3x}\,dx\)
- \(\displaystyle v=∫\dfrac{2}{3}e^{3x}\,dx=\dfrac{2}{9}e^{3x}.\)
Substituindo novamente na Equação\ ref {3A.2} produz
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\left(\dfrac{2}{9}xe^{3x}−∫\dfrac{2}{9}e^{3x}\,dx\right). \nonumber \]
Depois de avaliar a última integral e simplificar, obtemos
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\dfrac{2}{9}xe^{3x}+\dfrac{2}{27}e^{3x}+C. \nonumber \]
Avalie
\[∫t^3e^{t^2}dt. \nonumber \]
Solução
Se usarmos uma interpretação estrita do Mnemônico LIATE para fazer nossa escolha\(u\), acabaremos com\(u=t^3\)\(dv=e^{t^2}dt\) e. Infelizmente, essa escolha não funcionará porque não podemos avaliar\(∫e^{t^2}dt\). No entanto, como podemos avaliar\(∫te^{t^2}\,dx\), podemos tentar escolher\(u=t^2\) e,\(dv=te^{t^2}dt.\) com essas escolhas, temos
- \(u=t^2\)
- \(du=2tdt\)
- \(dv=te^{t^2}dt\)
- \(v=∫te^{t^2}dt=\dfrac{1}{2}e^{t^2}.\)
Assim, obtemos
\[\begin{align*} ∫t^3e^{t^2}dt =\dfrac{1}{2}t^2e^{t^2}−∫\dfrac{1}{2}e^{t^2}2t\,dt \\[4pt] =\dfrac{1}{2}t^2e^{t^2}−\dfrac{1}{2}e^{t^2}+C. \end{align*}\]
Avalie\[∫\sin (\ln x)\,dx. \nonumber \]
Solução
Essa integral parece ter apenas uma função - a saber,\(\sin (\ln x)\) - no entanto, sempre podemos usar a função constante 1 como a outra função. Neste exemplo, vamos escolher\(u=\sin (\ln x)\)\(dv=1\,dx\) e. (A decisão de usar\(u=\sin (\ln x)\) é fácil. Não podemos escolher\(dv=\sin (\ln x)\,dx\) porque, se pudéssemos integrá-la, não estaríamos usando a integração por partes em primeiro lugar!) Consequentemente,\(du=(1/x)\cos (\ln x) \,dx\) e\(v=∫ 1 \,dx=x.\) depois de aplicar a integração por partes ao integral e simplificar, temos
\[∫\sin \left(\ln x\right) \,dx=x \sin (\ln x)−\int \cos (\ln x)\,dx. \nonumber \]
Infelizmente, esse processo nos deixa com uma nova integral muito semelhante à original. No entanto, vamos ver o que acontece quando aplicamos a integração por partes novamente. Desta vez, vamos escolher\(u=\cos (\ln x)\) e\(dv=1\,dx,\) fazer\(du=−(1/x)\sin (\ln x)\,dx\) e\(v=∫1\,dx=x.\)
Substituindo, temos
\[∫\sin (\ln x)\,dx=x \sin (\ln x)−(x \cos (\ln x)-∫−\sin (\ln x)\,dx). \nonumber \]
Depois de simplificar, obtemos
\[∫\sin (\ln x)\,dx=x\sin (\ln x)−x \cos (\ln x)−∫\sin (\ln x)\,dx. \nonumber \]
A última integral agora é a mesma que a original. Pode parecer que simplesmente fizemos um círculo, mas agora podemos realmente calcular a integral. Para ver como fazer isso com mais clareza, substitua\(I=∫\sin (\ln x)\,dx.\) Assim, a equação se torna
\[I=x \sin (\ln x)−x \cos (\ln x)−I. \nonumber \]
Primeiro, adicione\(I\) aos dois lados da equação para obter
\[2I=x \sin (\ln x)−x \cos (\ln x). \nonumber \]
Em seguida, divida por 2:
\[I=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber \]
Substituindo\(I=∫\sin (\ln x)\,dx\) novamente, temos
\[ \int \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber \]
A partir disso, vemos que\((1/2)x \sin (\ln x)−(1/2)x \cos (\ln x)\) é uma antiderivada de\(\sin (\ln x)\,dx\). Para a antiderivada mais geral, adicione\(+C\):
\[ ∫ \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x)+C. \nonumber \]
Análise
Se esse método parecer um pouco estranho no início, podemos verificar a resposta por diferenciação:
\[\begin{align*} \dfrac{d}{\,dx}\left(\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x\cos (\ln x)\right) \\[4pt] &=\dfrac{1}{2}(\sin (\ln x))+\cos (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x−\left(\dfrac{1}{2}\cos (\ln x)−\sin (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x\right) \\[4pt] &=\sin (\ln x). \end{align*}\]
Avalie\[∫x^2\sin x\,dx. \nonumber \]
- Dica
-
Isso é semelhante a Exemplos\(\PageIndex{3A}\) -\(\PageIndex{3C}\).
- Resposta
-
\[∫x^2\sin x\,dx=−x^2\cos x+2x\sin x+2\cos x+C \nonumber \]
Integração por peças para integrais definidas
Agora que usamos a integração por partes com sucesso para avaliar integrais indefinidas, voltamos nossa atenção para integrais definidas. A técnica de integração é realmente a mesma, só que adicionamos uma etapa para avaliar a integral nos limites superior e inferior da integração.
Funções let\(u=f(x)\) and\(v=g(x)\) be com derivadas contínuas em [\(a,b\)]. Então
\[∫^b_a u\,dv=uv\Big|^b_a−∫^b_a v\, du \nonumber \]
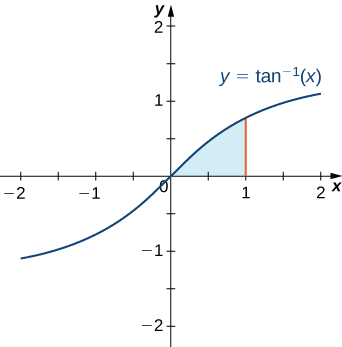
Encontre a área da região delimitada acima pelo gráfico de\(y=\tan^{−1}x\) e abaixo pelo\(x\) eixo -no intervalo [\(0,1\)].
Solução
Essa região é mostrada na Figura\(\PageIndex{1}\). Para encontrar a área, devemos avaliar
\[∫^1_0 \tan^{−1}x\, \,dx. \nonumber \]
Para essa integral, vamos escolher\(u=tan^{−1}x\) e\(dv=\,dx\), assim, fazer\(du=\dfrac{1}{x^2+1}\,dx\)\(v=x\) e. Depois de aplicar a fórmula de integração por partes (Equação\ ref {IBP}), obtemos
\[ \text{Area}=\left. x \tan^{−1} x \right|^1_0−∫^1_0 \dfrac{x}{x^2+1} \,dx. \nonumber \]
Use\(u\) -substitution para obter
\[∫^1_0\dfrac{x}{x^2+1}\,dx=\left.\dfrac{1}{2}\ln \left(x^2+1\right) \right|^1_0. \nonumber \]
Assim,
\[\text{Area}=x \tan^{−1}x \Big|^1_0− \left.\dfrac{1}{2}\ln \left( x^2+1 \right) \right|^1_0=\left(\dfrac{π}{4}−\dfrac{1}{2}\ln 2\right) \,\text{units}^2. \nonumber \]
Nesse ponto, pode não ser uma má ideia fazer uma “verificação da realidade” sobre a razoabilidade de nossa solução. Como\(\dfrac{π}{4}−\dfrac{1}{2}\ln 2≈0.4388\,\text{units}^2,\) e a partir da Figura,\(\PageIndex{1}\) esperamos que nossa área seja um pouco menor do que\(0.5\,\text{units}^2,\) essa solução parece ser razoável.
Encontre o volume do sólido obtido girando a região delimitada pelo gráfico\(f(x)=e^{−x},\) do\(x\) eixo -, do\(y\) eixo -e pela linha ao\(x=1\) redor do\(y\) eixo.
Solução
A melhor opção para resolver esse problema é usar o método shell. Comece desenhando a região a ser revolvida, junto com um retângulo típico (Figura\(\PageIndex{2}\)).
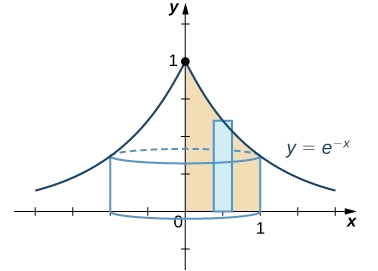
Para encontrar o volume usando conchas, devemos avaliar
\[2π∫^1_0xe^{−x}\,dx. \label{4B.1} \]
Para fazer isso, deixe\(u=x\)\(dv=e^{−x}\) e. Essas escolhas levam\(du=\,dx\) e\(v=∫e^{−x}\,dx=−e^{−x}.\) Usando a fórmula do Método Shell, obtemos
\ [\ begin {align*}\ text {Volume} &=2π ^1_0xe^ {−x}\, dx\\ [4pt] = 2π\ left (−xe^ {−x}\ big|^1_0+^1_0e^ {−x}\, dx\ right)\ tag {Use a integração por partes}\\ [4pt]
&= 2π\ left (-e^ {-1} + 0 - e^ {-x}\ Big|^1_0\ direita)\\ [4pt]
&= 2π\ left (-e^ {-1} - e^ {-1} + 1\ direita)\\ [4pt]
&= 2π\ left (1 -\ dfrac {2} {e}\ right)\,\ text {unidades} ^3. \ tag {Avalie e simplifique}\ end {align*}\]
Análise
Novamente, é uma boa ideia verificar a razoabilidade da nossa solução. Observamos que o sólido tem um volume um pouco menor que o de um cilindro de raio\(1\) e altura de\(1/e\) adicionado ao volume de um cone de raio base\(1\) e altura de\(1−\dfrac{1}{e}.\) Consequentemente, o sólido deve ter um volume um pouco menor que
\[π(1)^2\dfrac{1}{e}+\left(\dfrac{π}{3}\right)(1)^2\left(1−\dfrac{1}{e}\right)=\dfrac{2π}{3e}+\dfrac{π}{3}≈1.8177\,\text{units}^3. \nonumber \]
Pois\(2π−\dfrac{4π}{e}≈1.6603,\) vemos que nosso volume calculado é razoável.
Avalie\[∫^{π/2}_0x\cos x\,dx. \nonumber \]
- Dica
-
Use a equação\ ref {IBP} com\(u=x\) e\(dv=\cos x\,dx.\)
- Resposta
-
\[∫^{π/2}_0x\cos x\,dx = \dfrac{π}{2}−1 \nonumber \]
Conceitos-chave
- A fórmula de integração por partes (Equação\ ref {IBP}) permite a troca de uma integral por outra, possivelmente mais fácil.
- A integração por partes se aplica a integrais definidos e indefinidos.
Equações-chave
- Fórmula de integração por peças
\(\displaystyle ∫u\,dv=uv−∫v\,du\)
- Integração por partes para integrais definidos
\(\displaystyle ∫^b_au\,dv=uv\Big|^b_a−∫^b_av\,du\)
Glossário
- integração por peças
- uma técnica de integração que permite a troca de uma integral por outra usando a fórmula\(\displaystyle ∫u\,dv=uv−∫v\,du\)


