Skip to main content
Global

7.1E: Exercícios para a Seção 7.1

  1. Last updated
  2. Save as PDF
  • Page ID
    188293

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Ao usar a técnica de integração por partes, você deve escolher cuidadosamente qual é a expressão\(u\). Para cada um dos problemas a seguir, use as diretrizes desta seção para escolher\(u\). Não avalie os integrais.

    1)\(\displaystyle ∫x^3e^{2x}\,dx\)

    Resposta
    \( u=x^3\)

    2)\(\displaystyle ∫x^3\ln(x)\,dx\)

    3)\(\displaystyle ∫y^3\cos y\,dy\)

    Resposta
    \(u=y^3\)

    4)\(\displaystyle ∫x^2\arctan x\,dx\)

    5)\(\displaystyle ∫e^{3x}\sin(2x)\,dx\)

    Resposta
    \(u=\sin(2x)\)

    Nos exercícios 6 a 37, encontre a integral usando o método mais simples. Nem todos os problemas exigem integração por partes.

    6)\(\displaystyle ∫v\sin v\,dv\)

    7)\(\displaystyle ∫\ln x\,dx\) (Dica:\(\displaystyle ∫\ln x\,dx\) é equivalente a\(\displaystyle ∫1⋅\ln(x)\,dx.)\)

    Resposta
    \(\displaystyle ∫\ln x\,dx \quad = \quad−x+x\ln x+C\)

    8)\(\displaystyle ∫x\cos x\,dx\)

    9)\(\displaystyle ∫\tan^{−1}x\,dx\)

    Resposta
    \(\displaystyle ∫\tan^{−1}x\,dx\quad = \quad x\tan^{−1}x−\tfrac{1}{2}\ln(1+x^2)+C\)

    10)\(\displaystyle ∫x^2e^x\,dx\)

    11)\(\displaystyle ∫x\sin(2x)\,dx\)

    Resposta
    \(\displaystyle ∫x\sin(2x)\,dx \quad = \quad −\tfrac{1}{2}x\cos(2x)+\tfrac{1}{4}\sin(2x)+C\)

    12)\(\displaystyle ∫xe^{4x}\,dx\)

    13)\(\displaystyle ∫xe^{−x}\,dx\)

    Resposta
    \(\displaystyle ∫xe^{−x}\,dx \quad = \quad e^{−x}(−1−x)+C\)

    14)\(\displaystyle ∫x\cos 3x\,dx\)

    15)\(\displaystyle ∫x^2\cos x\,dx\)

    Resposta
    \(\displaystyle ∫x^2\cos x\,dx \quad = \quad 2x\cos x+(−2+x^2)\sin x+C\)

    16)\(\displaystyle ∫x\ln x\,dx\)

    17)\(\displaystyle ∫\ln(2x+1)\,dx\)

    Resposta
    \(\displaystyle ∫\ln(2x+1)\,dx \quad = \quad \tfrac{1}{2}(1+2x)(−1+\ln(1+2x))+C\)

    18)\(\displaystyle ∫x^2e^{4x}\,dx\)

    19)\(\displaystyle ∫e^x\sin x\,dx\)

    Resposta
    \(\displaystyle ∫e^x\sin x\,dx \quad = \quad \tfrac{1}{2}e^x(−\cos x+\sin x)+C\)

    20)\(\displaystyle ∫e^x\cos x\,dx\)

    21)\(\displaystyle ∫xe^{−x^2}\,dx\)

    Resposta
    \(\displaystyle ∫xe^{−x^2}\,dx \quad = \quad −\frac{e^{−x^2}}{2}+C\)

    22)\(\displaystyle ∫x^2e^{−x}\,dx\)

    23)\(\displaystyle ∫\sin(\ln(2x))\,dx\)

    Resposta
    \(\displaystyle ∫\sin(\ln(2x))\,dx \quad = \quad −\tfrac{1}{2}x\cos[\ln(2x)]+\tfrac{1}{2}x\sin[\ln(2x)]+C\)

    24)\(\displaystyle ∫\cos(\ln x)\,dx\)

    25)\(\displaystyle ∫(\ln x)^2\,dx\)

    Resposta
    \(\displaystyle ∫(\ln x)^2\,dx \quad = \quad 2x−2x\ln x+x(\ln x)^2+C\)

    26)\(\displaystyle ∫\ln(x^2)\,dx\)

    27)\(\displaystyle ∫x^2\ln x\,dx\)

    Responda
    \(\displaystyle ∫x^2\ln x\,dx \quad = \quad −\frac{x^3}{9}+\tfrac{1}{3}x^3\ln x+C\)

    28)\(\displaystyle ∫\sin^{−1}x\,dx\)

    29)\(\displaystyle ∫\cos^{−1}(2x)\,dx\)

    Responda
    \(\displaystyle ∫\cos^{−1}(2x)\,dx \quad = \quad −\tfrac{1}{2}\sqrt{1−4x^2}+x\cos^{−1}(2x)+C\)

    30)\(\displaystyle ∫x\arctan x\,dx\)

    31)\(\displaystyle ∫x^2\sin x\,dx\)

    Responda
    \(\displaystyle ∫x^2\sin x\,dx \quad = \quad −(−2+x^2)\cos x+2x\sin x+C\)

    32)\(\displaystyle ∫x^3\cos x\,dx\)

    33)\(\displaystyle ∫x^3\sin x\,dx\)

    Responda
    \(\displaystyle ∫x^3\sin x\,dx \quad = \quad −x(−6+x^2)\cos x+3(−2+x^2)\sin x+C\)

    34)\(\displaystyle ∫x^3e^x\,dx\)

    (35)\(\displaystyle ∫x\sec^{−1}x\,dx\)

    Responda
    \(\displaystyle ∫x\sec^{−1}x\,dx \quad = \quad \tfrac{1}{2}x\left(−\sqrt{1−\frac{1}{x^2}}+x⋅\sec^{−1}x\right)+C\)

    36)\(\displaystyle ∫x\sec^2x\,dx\)

    37)\(\displaystyle ∫x\cosh x\,dx\)

    Responda
    \(\displaystyle ∫x\cosh x\,dx \quad = \quad −\cosh x+x\sinh x+C\)

    Nos exercícios 38 a 46, calcule as integrais definidas. Use um utilitário gráfico para confirmar suas respostas.

    38)\(\displaystyle ∫^1_{1/e}\ln x\,dx\)

    39)\(\displaystyle ∫^1_0xe^{−2x}\,dx\) (Expresse a resposta na forma exata.)

    Responda
    \(\displaystyle ∫^1_0xe^{−2x}\,dx \quad = \quad \frac{1}{4}−\frac{3}{4e^2}\)

    40)\(\displaystyle ∫^1_0e^{\sqrt{x}}\,dx \quad (\text{let}\, u=\sqrt{x})\)

    41)\(\displaystyle ∫^e_1\ln(x^2)\,dx\)

    Responda
    \(\displaystyle ∫^e_1\ln(x^2)\,dx \quad = \quad 2\)

    (42)\(\displaystyle ∫^π_0x\cos x\,dx\)

    43)\(\displaystyle ∫^π_{−π}x\sin x\,dx\) (Expresse a resposta na forma exata.)

    Responda
    \(\displaystyle ∫^π_{−π}x\sin x\,dx \quad = \quad 2\pi\)

    44)\(\displaystyle ∫^3_0\ln(x^2+1)\,dx\) (Expresse a resposta na forma exata.)

    45)\(\displaystyle ∫^{π/2}_0x^2\sin x\,dx\) (Expresse a resposta na forma exata.)

    Responda
    \(\displaystyle ∫^{π/2}_0x^2\sin x\,dx \quad = \quad −2+π\)

    46)\(\displaystyle ∫^1_0x5^x\,dx\) (Expresse a resposta usando cinco dígitos significativos.)

    47) Avalie\(\displaystyle ∫\cos x\ln(\sin x)\,dx\)

    Responda
    \(\displaystyle ∫\cos x\ln(\sin x)\,dx \quad = \quad −\sin(x)+\ln[\sin(x)]\sin x+C\)

    Nos exercícios 48 a 50, extraia as seguintes fórmulas usando a técnica de integração por partes. Suponha que\(n\) seja um número inteiro positivo. Essas fórmulas são chamadas de fórmulas de redução porque o expoente no\(x\) termo foi reduzido em um em cada caso. A segunda integral é mais simples do que a integral original.

    48)\(\displaystyle ∫x^ne^x\,dx=x^ne^x−n∫x^{n−1}e^x\,dx\)

    49)\(\displaystyle ∫x^n\cos x\,dx=x^n\sin x−n∫x^{n−1}\sin x\,dx\)

    Responda
    As respostas variam

    50)\(\displaystyle ∫x^n\sin x\,dx=\) ______

    51) Integre\(\displaystyle ∫2x\sqrt{2x−3}\,dx\) usando dois métodos:

    a. Usando peças, deixando\(dv=\sqrt{2x−3}\,dx\)

    b. Substituição, locação\(u=2x−3\)

    Responda
    a.\(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)
    b.\(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)

    Nos exercícios 52 a 57, indique se você usaria a integração por partes para avaliar a integral. Em caso afirmativo, identifique\(u\)\(dv\) e. Caso contrário, descreva a técnica usada para realizar a integração sem realmente resolver o problema.

    52)\(\displaystyle ∫x\ln x\,dx\)

    53)\(\displaystyle ∫\frac{\ln^2x}{x}\,dx\)

    Responda
    Não use a integração por partes. Escolha\(u\) ser\(\ln x\), e a integral é da forma\(\displaystyle ∫u^2\,du.\)

    54)\(\displaystyle ∫xe^x\,dx\)

    55)\(\displaystyle ∫xe^{x^2−3}\,dx\)

    Responda
    Não use a integração por partes. Deixe\(u=x^2−3\), e a integral pode ser colocada no formulário\(∫e^u\,du\).

    56)\(\displaystyle ∫x^2\sin x\,dx\)

    57)\(\displaystyle ∫x^2\sin(3x^3+2)\,dx\)

    Responda
    Não use a integração por partes. Escolha\(u\) ser\(u=3x^3+2\) e a integral pode ser colocada no formulário\(\displaystyle ∫\sin(u)\,du.\)

    Nos exercícios 58-59, desenhe a região delimitada acima pela curva, pelo\(x\) eixo -e\(x=1\), e encontre a área da região. Forneça o formulário exato ou as respostas arredondadas para o número de vagas indicado.

    58)\(y=2xe^{−x}\) (Resposta aproximada a quatro casas decimais.)

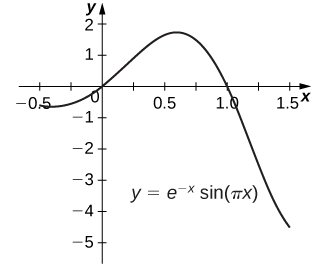
    59)\(y=e^{−x}\sin(πx)\) (Resposta aproximada a cinco casas decimais.)

    Responda
    A área abaixo do gráfico é\(0.39535 \, \text{units}^2.\)

    Nos exercícios 60 a 61, encontre o volume gerado pela rotação da região delimitada pelas curvas dadas em torno da linha especificada. Expresse as respostas na forma exata ou aproximada ao número de casas decimais indicado.

    60)\(y=\sin x,\,y=0,\,x=2π,\,x=3π;\) sobre o\(y\) eixo -( Expresse a resposta na forma exata.)

    61)\(y=e^{−x}, \,y=0,\,x=−1, \, x=0;\) sobre\(x=1\) (Expresse a resposta na forma exata.)

    Responda
    \(V = 2πe \, \text{units}^3\)

    62) Uma partícula que se move ao longo de uma linha reta tem uma velocidade de\(v(t)=t^2e^{−t}\) após o\(t\) segundo. Até onde ele viaja nos primeiros 2 segundos? (Suponha que as unidades estejam em pés e expresse a resposta na forma exata.)

    63) Encontre a área abaixo do gráfico de\(y=\sec^3x\) de\(x=0\) até\(x=1\). (Arredonde a resposta para dois dígitos significativos.)

    Responda
    \(A= 2.05 \, \text{units}^2\)

    64) Encontre a área entre\(y=(x−2)e^x\) e o\(x\) eixo\(x=2\) -de\(x=5\) a. (Expresse a resposta na forma exata.)

    65) Encontre a área da região delimitada pela curva\(y=x\cos x\) e o\(x\) eixo -para\(\frac{11π}{2}≤x≤\frac{13π}{2}.\) (Expresse a resposta na forma exata.)

    Responda
    \(A = 12π \, \text{units}^2\)

    66) Encontre o volume do sólido gerado pela rotação da região delimitada pela curva\(y=\ln x\), pelo\(x\) eixo -e pela linha vertical em\(x=e^2\) torno do\(x\) eixo. (Expresse a resposta na forma exata.)

    67) Encontre o volume do sólido gerado pela rotação da região delimitada pela curva\(y=4\cos x\) e pelo \(x\)eixo -, em\(\frac{π}{2}≤x≤\frac{3π}{2},\) torno do\(x\) eixo -. (Expresse a resposta na forma exata.)

    Responda
    \(V = 8π^2 \, \text{units}^3\)

    68) Encontre o volume do sólido gerado girando a região no primeiro quadrante delimitada por\(y=e^x\) e o\(x\) eixo -, de\(x=0\) para\(x=\ln(7)\), em torno do\(y\) eixo -. (Expresse a resposta na forma exata.)

    69) Qual é o volume do bolo Bundt que vem da rotação\( y=\sin x\) em torno do\(y\) eixo -de\( x=0\) para\( x=π\)?

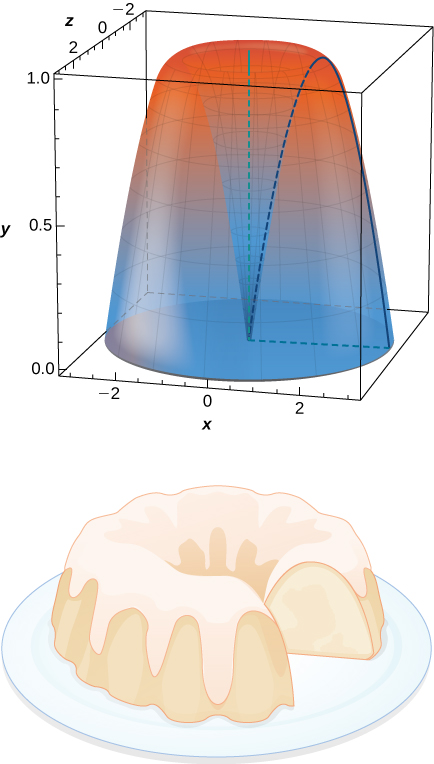
    Resposta
    \(V = 2π^2\)unidades 3