6.9: Cálculo das funções hiperbólicas

Last updated
Save as PDF

Page ID: 187825

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Aplique as fórmulas para derivadas e integrais das funções hiperbólicas.
Aplique as fórmulas para as derivadas das funções hiperbólicas inversas e suas integrais associadas.
Descreva as condições comuns aplicadas de uma curva catenária.

Fomos apresentados às funções hiperbólicas anteriormente, juntamente com algumas de suas propriedades básicas. Nesta seção, examinamos as fórmulas de diferenciação e integração para as funções hiperbólicas e seus inversos.

Derivadas e integrais das funções hiperbólicas

Lembre-se de que o seno hiperbólico e o cosseno hiperbólico são definidos como

\[\sinh x=\dfrac{e^x−e^{−x}}{2} \nonumber \]

\[\cosh x=\dfrac{e^x+e^{−x}}{2}. \nonumber \]

As outras funções hiperbólicas são então definidas em termos de\(\sinh x\)\(\cosh x\) e. Os gráficos das funções hiperbólicas são mostrados na Figura\(\PageIndex{1}\).

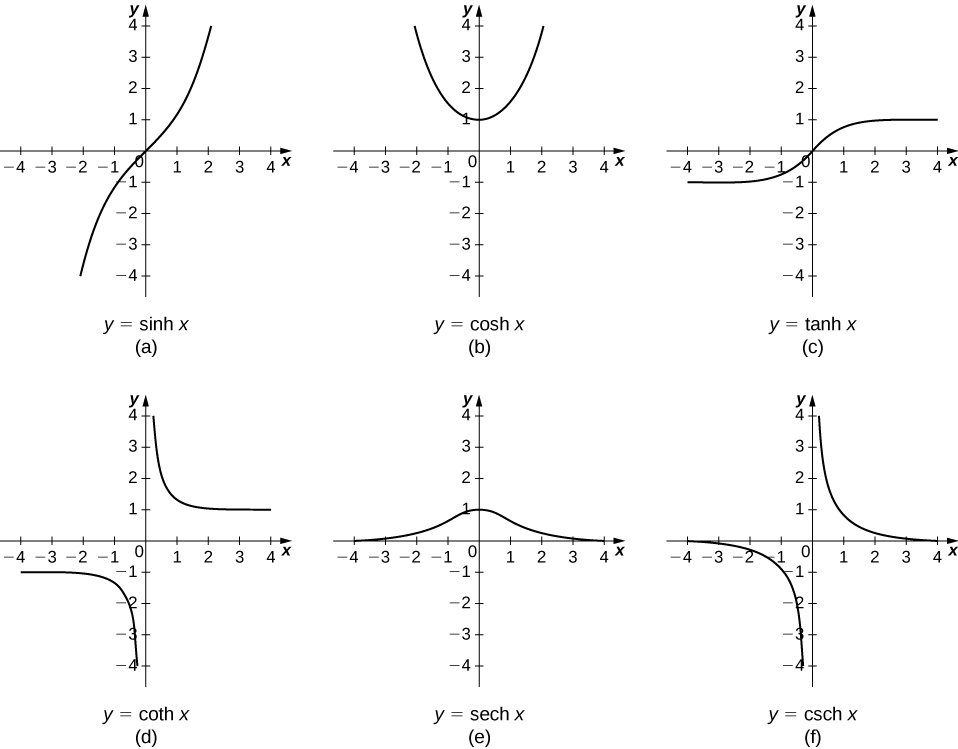
Essa figura tem seis gráficos. O primeiro gráfico chamado “a” é da função y=sinh (x). É uma função crescente do 3º quadrante, passando pela origem até o primeiro quadrante. O segundo gráfico é rotulado como “b” e é da função y=cosh (x). Ela diminui no segundo quadrante até o intercepto y=1, depois se torna uma função crescente. O terceiro gráfico chamado “c” é da função y=tanh (x). É uma função crescente do terceiro quadrante, passando pela origem, até o primeiro quadrante. O quarto gráfico é rotulado como “d” e é da função y=coth (x). Tem duas peças, uma no terceiro quadrante e outra no primeiro quadrante com uma assíntota vertical no eixo y. O quinto gráfico é rotulado como “e” e é da função y=sech (x). É uma curva acima do eixo x, aumentando no segundo quadrante, para o eixo y em y = 1 e depois diminui. O sexto gráfico é rotulado como “f” e é da função y=csch (x). Tem duas peças, uma no terceiro quadrante e outra no primeiro quadrante com uma assíntota vertical no eixo y. — Figura\(\PageIndex{1}\): Gráficos das funções hiperbólicas.

É fácil desenvolver fórmulas de diferenciação para as funções hiperbólicas. Por exemplo, olhando para\(\sinh x\) nós temos

\[\begin{align*} \dfrac{d}{dx} \left(\sinh x \right) &=\dfrac{d}{dx} \left(\dfrac{e^x−e^{−x}}{2}\right) \\[4pt] &=\dfrac{1}{2}\left[\dfrac{d}{dx}(e^x)−\dfrac{d}{dx}(e^{−x})\right] \\[4pt] &=\dfrac{1}{2}[e^x+e^{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]

Da mesma forma,

\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

Resumimos as fórmulas de diferenciação para as funções hiperbólicas na Tabela\(\PageIndex{1}\).

Tabela\(\PageIndex{1}\): Derivadas das funções hiperbólicas
\(f(x)\)	\(\dfrac{d}{dx}f(x)\)
\ (f (x)\)” style="alinhamento do texto: centro; ">\(\sinh x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(\cosh x\)
\ (f (x)\)” style="alinhamento do texto: centro; ">\(\cosh x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(\sinh x\)
\ (f (x)\)” style="alinhamento do texto: centro; ">\(\tanh x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(\text{sech}^2 \,x\)
\ (f (x)\)” style="alinhamento do texto: centro; ">\(\text{coth } x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(−\text{csch}^2\, x\)
\ (f (x)\)” style="alinhamento do texto: centro; ">\(\text{sech } x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(−\text{sech}\, x \tanh x\)
\ (f (x)\)” style="alinhamento do texto: centro; ">\(\text{csch } x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:center; ">\(−\text{csch}\, x \coth x\)

Vamos parar um momento para comparar as derivadas das funções hiperbólicas com as derivadas das funções trigonométricas padrão. Há muitas semelhanças, mas também diferenças. Por exemplo, as derivadas das funções senoidais correspondem a:

\[\dfrac{d}{dx} \sin x=\cos x \nonumber \]

\[\dfrac{d}{dx} \sinh x=\cosh x. \nonumber \]

As derivadas das funções do cosseno, no entanto, diferem no sinal:

\[\dfrac{d}{dx} \cos x=−\sin x, \nonumber \]

mas

\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

À medida que continuamos nosso exame das funções hiperbólicas, devemos estar atentos às suas semelhanças e diferenças com as funções trigonométricas padrão. Essas fórmulas de diferenciação para as funções hiperbólicas levam diretamente às seguintes fórmulas integrais.

\[ \begin{align} \int \sinh u \,du &=\cosh u+C \\[4pt] \int \text{csch}^2 u \, du &=−\coth u+C \\[4pt] \int \cosh u \,du &=\sinh u+C \\[4pt] \int \text{sech} \,u \tanh u \,du &=−\text{sech } \,u+C−\text{csch} \,u+C \\[4pt] \int \text{sech }^2u \,du &=\tanh u+C \\[4pt] \int \text{csch} \,u \coth u \,du &=−\text{csch} \,u+C \end{align} \nonumber \]

Exemplo\(\PageIndex{1}\): Differentiating Hyperbolic Functions

Avalie as seguintes derivadas:

\(\dfrac{d}{dx}(\sinh(x^2))\)
\(\dfrac{d}{dx}(\cosh x)^2\)

Solução:

Usando as fórmulas na Tabela\(\PageIndex{1}\) e a regra da cadeia, obtemos

\(\dfrac{d}{dx}(\sinh(x^2))=\cosh(x^2)⋅2x\)
\(\dfrac{d}{dx}(\cosh x)^2=2\cosh x\sinh x\)

Exercício\(\PageIndex{1}\)

Avalie as seguintes derivadas:

\(\dfrac{d}{dx}(\tanh(x^2+3x))\)
\(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)\)

Dica: Use as fórmulas na Tabela\(\PageIndex{1}\) e aplique a regra da cadeia conforme necessário.
Responda a um: \(\dfrac{d}{dx}(\tanh(x^2+3x))=(\text{sech}^2(x^2+3x))(2x+3)\)
Resposta b: \(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)=\dfrac{d}{dx}(\sinh x)^{−2}=−2(\sinh x)^{−3}\cosh x\)

Exemplo\(\PageIndex{2}\): Integrals Involving Hyperbolic Functions

Avalie as seguintes integrais:

\( \displaystyle \int x\cosh(x^2)dx\)
\( \displaystyle \int \tanh x\,dx\)

Solução

Podemos usar\(u\) -substitution em ambos os casos.

a. Deixe\(u=x^2\). Em seguida,\(du=2x\,dx\) e

\[\begin{align*} \int x\cosh (x^2)dx &=\int \dfrac{1}{2}\cosh u\,du \\[4pt] &=\dfrac{1}{2}\sinh u+C \\[4pt] &=\dfrac{1}{2}\sinh (x^2)+C. \end{align*}\]

b. Esquerda\(u=\cosh x\). Em seguida,\(du=\sinh x\,dx\) e

\[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C.\end{align*}\]

Observe que,\(\cosh x>0\) para todos\(x\), podemos eliminar os sinais de valor absoluto e obter

\[\int \tanh x \,dx=\ln(\cosh x)+C. \nonumber \]

Exercício\(\PageIndex{2}\)

Avalie as seguintes integrais:

\(\displaystyle \int \sinh^3x \cosh x \,dx\)
\(\displaystyle \int \text{sech }^2(3x)\, dx\)

Dica: Use as fórmulas acima e aplique\(u\) -substitution conforme necessário.
Responda a um: \(\displaystyle \int \sinh^3x \cosh x \,dx=\dfrac{\sinh^4x}{4}+C\)
Resposta b: \(\displaystyle \int \text{sech }^2(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)

Cálculo de funções hiperbólicas inversas

Observando os gráficos das funções hiperbólicas, vemos que, com restrições de alcance apropriadas, todas elas têm inversas. A maioria das restrições de alcance necessárias pode ser discernida examinando minuciosamente os gráficos. Os domínios e intervalos das funções hiperbólicas inversas estão resumidos na Tabela\(\PageIndex{2}\).

Tabela\(\PageIndex{2}\): Domínios e intervalos das funções hiperbólicas inversas
Função	Domínio	Alcance
\(\sinh^{−1}x\)	(−∞, ∞)	(−∞, ∞)
\(\cosh^{−1}x\)	(1, ∞)	[0, ∞)
\(\tanh^{−1}x\)	(−1,1)	(−∞, ∞)
\(\coth^{−1}x\)	(−,1) (1, ∞)	(−,0) (0, ∞)
\(\text{sech}^{−1}x\)	(0,1)	[0, ∞)
\(\text{csch}^{−1}x\)	(−,0) (0, ∞)	(−,0) (0, ∞)

Os gráficos das funções hiperbólicas inversas são mostrados na figura a seguir.

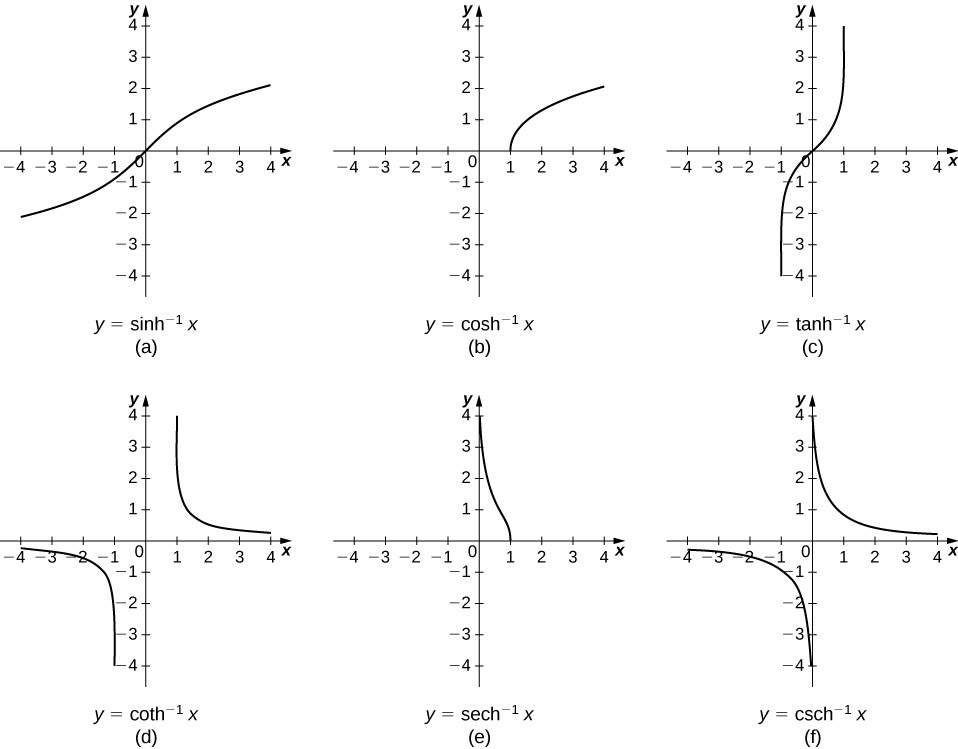
Essa figura tem seis gráficos. O primeiro gráfico chamado “a” é da função y=sinh^-1 (x). É uma função crescente do 3º quadrante, passando pela origem até o primeiro quadrante. O segundo gráfico é rotulado como “b” e é da função y=cosh^-1 (x). Está no primeiro quadrante, começando no eixo x em 2 e aumentando. O terceiro gráfico chamado “c” é da função y=tanh^-1 (x). É uma função crescente do terceiro quadrante, passando pela origem, até o primeiro quadrante. O quarto gráfico é rotulado como “d” e é da função y=coth^-1 (x). Tem duas peças, uma no terceiro quadrante e outra no primeiro quadrante com uma assíntota vertical no eixo y. O quinto gráfico é rotulado como “e” e é da função y=sech^-1 (x). É uma curva diminuindo no primeiro quadrante e parando no eixo x em x=1. O sexto gráfico é rotulado como “f” e é da função y=csch^-1 (x). Tem duas peças, uma no terceiro quadrante e outra no primeiro quadrante com uma assíntota vertical no eixo y. — Figura\(\PageIndex{3}\): Gráficos das funções hiperbólicas inversas.

Para encontrar as derivadas das funções inversas, usamos a diferenciação implícita. Nós temos

\[\begin{align} y &=\sinh^{−1}x \\[4pt] \sinh y &=x \\[4pt] \dfrac{d}{dx} \sinh y &=\dfrac{d}{dx}x \\[4pt] \cosh y\dfrac{dy}{dx} &=1. \end{align} \nonumber \]

Lembre-se disso\(\cosh y=\sqrt{1+\sinh^2y}\).\(\cosh^2y−\sinh^2y=1,\) Então,

\[\dfrac{dy}{dx}=\dfrac{1}{\cosh y}=\dfrac{1}{\sqrt{1+\sinh^2y}}=\dfrac{1}{\sqrt{1+x^2}}. \nonumber \]

Podemos derivar fórmulas de diferenciação para as outras funções hiperbólicas inversas de forma semelhante. Essas fórmulas de diferenciação estão resumidas na Tabela\(\PageIndex{3}\).

Tabela\(\PageIndex{3}\): Derivadas das funções hiperbólicas inversas
\(f(x)\)	\(\dfrac{d}{dx}f(x)\)
\ (f (x)\)” style="alinhamento vertical:meio; ">\(\sinh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="alinhamento vertical: meio; ">\(\dfrac{1}{\sqrt{1+x^2}}\)
\ (f (x)\)” style="alinhamento vertical:meio; ">\(\cosh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="alinhamento vertical: meio; ">\(\dfrac{1}{\sqrt{x^2−1}}\)
\ (f (x)\)” style="alinhamento vertical:meio; ">\(\tanh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="alinhamento vertical: meio; ">\(\dfrac{1}{1−x^2}\)
\ (f (x)\)” style="alinhamento vertical:meio; ">\(\coth^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="alinhamento vertical: meio; ">\(\dfrac{1}{1−x^2}\)
\ (f (x)\)” style="alinhamento vertical:meio; ">\(\text{sech}^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="alinhamento vertical: meio; ">\(\dfrac{−1}{x\sqrt{1−x^2}}\)
\ (f (x)\)” style="alinhamento vertical:meio; ">\(\text{csch}^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="alinhamento vertical: meio; ">\(\dfrac{−1}{\|x\|\sqrt{1+x^2}}\)

Observe que as derivadas de\(\tanh^{−1}x\) e\(\coth^{−1}x\) são as mesmas. Assim, quando integramos\(1/(1−x^2)\), precisamos selecionar a antiderivada adequada com base no domínio das funções e nos valores de\(x\). As fórmulas de integração envolvendo as funções hiperbólicas inversas são resumidas da seguinte forma.

\[\int \dfrac{1}{\sqrt{1+u^2}}du=\sinh^{−1}u+C \nonumber \]

\[\int \dfrac{1}{u\sqrt{1−u^2}}du=−\text{sech}^{−1}|u|+C \nonumber \]

\[\int \dfrac{1}{\sqrt{u^2−1}}du=\cosh^{−1}u+C \nonumber \]

\[\int \dfrac{1}{u\sqrt{1+u^2}}du=−\text{csch}^{−1}|u|+C \nonumber \]

\[\int \dfrac{1}{1−u^2}du=\begin{cases}\tanh^{−1}u+C & \text{if }|u|<1\\ \coth^{−1}u+C & \text{if }|u|>1\end{cases} \nonumber \]

Exemplo\(\PageIndex{3}\): Differentiating Inverse Hyperbolic Functions

Avalie as seguintes derivadas:

\(\dfrac{d}{dx}\left(\sinh^{−1}\left(\dfrac{x}{3}\right)\right)\)
\(\dfrac{d}{dx}\left(\tanh^{−1}x\right)^2\)

Solução

Usando as fórmulas na Tabela\(\PageIndex{3}\) e a regra da cadeia, obtemos os seguintes resultados:

\(\dfrac{d}{dx}(\sinh^{−1}(\dfrac{x}{3}))=\dfrac{1}{3\sqrt{1+\dfrac{x^2}{9}}}=\dfrac{1}{\sqrt{9+x^2}}\)
\(\dfrac{d}{dx}(\tanh^{−1}x)^2=\dfrac{2(\tanh^{−1}x)}{1−x^2}\)

Exercício\(\PageIndex{3}\)

Avalie as seguintes derivadas:

\(\dfrac{d}{dx}(\cosh^{−1}(3x))\)
\(\dfrac{d}{dx}(\coth^{−1}x)^3\)

Dica: Use as fórmulas na Tabela\(\PageIndex{3}\) e aplique a regra da cadeia conforme necessário.
Responda a um: \(\dfrac{d}{dx}(\cosh^{−1}(3x))=\dfrac{3}{\sqrt{9x^2−1}} \)
Resposta b: \(\dfrac{d}{dx}(\coth^{−1}x)^3=\dfrac{3(\coth^{−1}x)^2}{1−x^2} \)

Exemplo\(\PageIndex{4}\): Integrals Involving Inverse Hyperbolic Functions

Avalie as seguintes integrais:

\(\displaystyle \int \dfrac{1}{\sqrt{4x^2−1}}dx\)
\(\displaystyle \int \dfrac{1}{2x\sqrt{1−9x^2}}dx\)

Solução

Podemos usar \(u\)-substitution em ambos os casos.

Deixe\(u=2x\). Então,\(du=2\,dx\) e nós temos

\[\begin{align*} \int \dfrac{1}{\sqrt{4x^2−1}}\,dx &=\int \dfrac{1}{2\sqrt{u^2−1}}\,du \\[4pt] &=\dfrac{1}{2}\cosh^{−1}u+C \\[4pt] &=\dfrac{1}{2}\cosh^{−1}(2x)+C. \end{align*} \nonumber \]

Let\(u=3x.\) Then,\(du=3\,dx\) e obtemos

\[\begin{align*} \int \dfrac{1}{2x\sqrt{1−9x^2}}dx &=\dfrac{1}{2}\int \dfrac{1}{u\sqrt{1−u^2}}du \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|u|+C \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|3x|+C \end{align*}\]

Exercício\(\PageIndex{4}\)

Avalie as seguintes integrais:

\(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx,x>2\)
\(\displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx\)

Dica: Use as fórmulas acima e aplique\(u\) -substitution conforme necessário.
Responda a um: \(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx=\cosh^{−1}(\dfrac{x}{2})+C\)
Resposta b: \( \displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx=−\text{sech}^{−1}(e^x)+C\)

Aplicações

Uma aplicação física das funções hiperbólicas envolve a suspensão de cabos. Se um cabo de densidade uniforme for suspenso entre dois suportes sem qualquer carga além de seu próprio peso, o cabo forma uma curva chamada catenária. Linhas elétricas de alta tensão, correntes penduradas entre dois postes e fios de uma teia de aranha formam catenárias. A figura a seguir mostra correntes penduradas em uma fileira de postes.

Uma imagem de correntes penduradas entre postes que assumem a forma de uma catenária. — Figura\(\PageIndex{3}\): As correntes entre esses postes assumem a forma de uma catenária. (crédito: modificação do trabalho pela OKFoundryCompany, Flickr)

As funções hiperbólicas podem ser usadas para modelar catenárias. Especificamente, as funções do formulário\(y=a\cdot \cosh(x/a)\) são catenárias. A figura\(\PageIndex{4}\) mostra o gráfico de\(y=2\cosh(x/2)\).

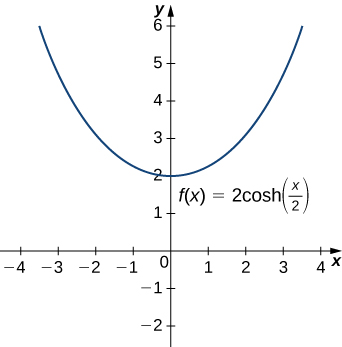
Essa figura é um gráfico. É da função f (x) =2cosh (x/2). A curva diminui no segundo quadrante até o eixo y. Ele cruza o eixo y em y=2. Em seguida, a curva aumenta. — Figura\(\PageIndex{4}\): Uma função de cosseno hiperbólico forma a forma de uma catenária.

Exemplo\(\PageIndex{5}\): Using a Catenary to Find the Length of a Cable

Suponha que um cabo suspenso tenha a forma\(10\cosh(x/10)\) de\(−15≤x≤15\), onde\(x\) é medido em pés. Determine o comprimento do cabo (em pés).

Solução

Lembre-se da Seção 6.4 que a fórmula para o comprimento do arco é

\[\underbrace{\int ^b_a\sqrt{1+[f′(x)]^2}dx}_{\text{Arc Length}}. \nonumber \]

Nós temos\(f(x)=10 \cosh(x/10)\), então\(f′(x)=\sinh(x/10)\). Então, o comprimento do arco é

\[\int ^b_a\sqrt{1+[f′(x)]^2}dx=\int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx. \nonumber \]

Agora lembre-se de que

\[1+\sinh^2x=\cosh^2x, \nonumber \]

então temos

\[\begin{align*} \text{Arc Length} &= \int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx \\[4pt] &=\int ^{15}_{−15}\cosh \left(\dfrac{x}{10}\right)dx \\[4pt] &= \left.10\sinh \left(\dfrac{x}{10}\right)\right|^{15}_{−15}\\[4pt] &=10\left[\sinh\left(\dfrac{3}{2}\right)−\sinh\left(−\dfrac{3}{2}\right)\right]\\[4pt] &=20\sinh \left(\dfrac{3}{2}\right) \\[4pt] &≈42.586\,\text{ft.} \end{align*}\]

Exercício\(\PageIndex{5}\):

Suponha que um cabo suspenso tenha o formato\(15 \cosh (x/15)\) para\(−20≤x≤20\). Determine o comprimento do cabo (em pés).

Resposta: \(52.95\)pés

Conceitos chave

As funções hiperbólicas são definidas em termos de funções exponenciais.
A diferenciação termo a termo produz fórmulas de diferenciação para as funções hiperbólicas. Essas fórmulas de diferenciação dão origem, por sua vez, a fórmulas de integração.
Com restrições de alcance apropriadas, todas as funções hiperbólicas têm inversas.
A diferenciação implícita produz fórmulas de diferenciação para as funções hiperbólicas inversas, que, por sua vez, dão origem a fórmulas de integração.
As aplicações físicas mais comuns das funções hiperbólicas são cálculos envolvendo catenárias.

Glossário

catenária: uma curva na forma da função\(y=a\cdot\cosh(x/a)\) é uma catenária; um cabo de densidade uniforme suspenso entre dois suportes assume a forma de uma catenária