6.6E: Exercícios para a Seção 6.6

Last updated
Save as PDF

Page ID: 187880

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 6, calcule o centro de massa para a coleta de massas dadas.

1)$m_1=2$ em$x_1=1$ e$m_2=4$ em$x_2=2$

2)$m_1=1$ em$x_1=−1$ e$m_2=3$ em$x_2=2$

Responda: $x = \frac{5}{4}$

3)$m=3$ em$x=0,1,2,6$

4) Massas unitárias em$(x,y)=(1,0),(0,1),(1,1)$

Responda: $\left(\frac{2}{3},\, \frac{2}{3}\right)$

5)$m_1=1$ em$(1,0)$ e$m_2=4$ em$(0,1)$

6)$m_1=1$ em$(1,0)$ e$m_2=3$ em$(2,2)$

Responda: $\left(\frac{7}{4},\,\frac{3}{2}\right)$

Nos exercícios 7 a 16, calcule o centro de massa$\bar x.$

7)$ρ=1$ para$x∈(−1,3)$

8)$ρ=x^2$ para$x∈(0,L)$

Responda: $\dfrac{3L}{4}$

9)$ρ=1$ para$x∈(0,1)$ e$ρ=2$ para$x∈(1,2)$

10)$ρ=\sin x$ para$x∈(0,π)$

Responda: $\frac{π}{2}$

11)$ρ=\cos x$ para$x∈\left(0,\frac{π}{2}\right)$

12)$ρ=e^x$ para$x∈(0,2)$

Responda: $\dfrac{e^2+1}{e^2−1}$

13)$ρ=x^3+xe^{−x}$ para$x∈(0,1)$

14)$ρ=x\sin x$ para$x∈(0,π)$

Responda: $\dfrac{π^2−4}{π}$

15)$ρ=\sqrt{x}$ para$x∈(1,4)$

16)$ρ=\ln x$ para$x∈(1,e)$

Responda: $\frac{1}{4}(1+e^2)$

Nos exercícios 17 a 19, calcule o centro de massa$(\bar{x},\bar{y}).$ Use simetria para ajudar a localizar o centro de massa sempre que possível.

17)$ρ=7$ na praça$0≤x≤1, \; 0≤y≤1$

18)$ρ=3$ no triângulo com vértices$(0,0), \, (a,0)$ e$(0,b)$

Responda: $\left(\frac{a}{3},\, \frac{b}{3}\right)$

19)$ρ=2$ para a região delimitada por$y=\cos(x), \; y=−\cos(x), \; x=−\frac{π}{2}$, e$x=\frac{π}{2}$

Nos exercícios 20 a 26, use uma calculadora para desenhar a região e, em seguida, calcule o centro de massa.$(\bar{x},\bar{y}).$ Use a simetria para ajudar a localizar o centro de massa sempre que possível.

20) [T] A região delimitada por$y=\cos(2x), \; x=−\frac{π}{4}$, e$x=\frac{π}{4}$

Responda: $\left(0,\frac{π}{8}\right)$

21) [T] A região entre$y=2x^2, \; y=0, \; x=0,$ e$x=1$

22) [T] A região entre$y=\frac{5}{4}x^2$ e$y=5$

Responda: $(0,3)$

23) [T] Região entre$y=\sqrt{x}, \; y=\ln x, \; x=1,$ e$x=4$

24) [T] A região delimitada por$y=0$ e$\dfrac{x^2}{4}+\dfrac{y^2}{9}=1$

Responda: $\left(0,\frac{4}{π}\right)$

25) [T] A região delimitada por$y=0, \; x=0,$ e$\dfrac{x^2}{4}+\dfrac{y^2}{9}=1$

26) [T] A região delimitada por$y=x^2$ e$y=x^4$ no primeiro quadrante

Responda: $\left(\frac{5}{8},\, \frac{1}{3}\right)$

Nos exercícios 27 a 31, use o teorema de Pappus para determinar o volume da forma.

27) Girando$y=mx$ em torno do$x$ eixo -entre$x=0$ e$x=1$

28) Girando$y=mx$ em torno do$y$ eixo -entre$x=0$ e$x=1$

Responda: $V = \frac{mπ}{3}$unidades³

29) Um cone geral criado pela rotação de um triângulo com vértices$(0,0), \, (a,0),$ e$(0,b)$ ao redor do$y$ eixo. Sua resposta concorda com o volume de um cone?

30) Um cilindro geral criado girando um retângulo com vértices$(0,0), \, (a,0), \, (0,b),$ e$(a,b)$ ao redor do$y$ eixo y. Sua resposta concorda com o volume de um cilindro?

Responda: $V = πa^2b$unidades³

31) Uma esfera criada pela rotação de um semicírculo com raio$a$ ao redor do$y$ eixo. Sua resposta concorda com o volume de uma esfera?

Nos exercícios 32 a 36, use uma calculadora para desenhar a região delimitada pela curva. Encontre a área$M$ e o centróide$(\bar{x},\bar{y})$ para as formas dadas. Use a simetria para ajudar a localizar o centro de massa sempre que possível.

32) [T] Quarto de círculo:$y=\sqrt{1−x^2}, \; y=0$, e$x=0$

Responda: $\left(\frac{4}{3π},\, \frac{4}{3π}\right)$

33) Triângulo [T]:$y=x, \; y=2−x$, e$y=0$

34) [T] Lente:$y=x^2$ e$y=x$

Responda: $\left(\frac{1}{2},\, \frac{2}{5}\right)$

35) [T] Anel:$y^2+x^2=1$ e$y^2+x^2=4$

36) [T] Meio anel:$y^2+x^2=1, \; y^2+x^2=4,$ e$y=0$

Responda: $\left(0,\, \frac{28}{9π}\right)$

37) Encontre o centro de massa generalizado na fatia entre$y=x^a$ e$y=x^b$ com$a>b$. Em seguida, use o teorema de Pappus para encontrar o volume do sólido gerado ao girar em torno do$y$ eixo.

38) Encontre o centro de massa generalizado entre$y=a^2−x^2, \; x=0$,$y=0$ e. Em seguida, use o teorema de Pappus para encontrar o volume do sólido gerado ao girar em torno do$y$ eixo.

Responda: Centro de massa:$\left(\frac{a}{6},\,\frac{4a^2}{5}\right),$
Volume:$\dfrac{2πa^4}{9}$ unidades³

39) Encontre o centro de massa generalizado entre$y=b\sin(ax),\; x=0,$ e$x=\dfrac{π}{a}.$ Então, use o teorema de Pappus para encontrar o volume do sólido gerado ao girar em torno do$y$ eixo.

40) Use o teorema de Pappus para encontrar o volume de um toróide (ilustrado aqui). Suponha que um disco de raio$a$ esteja posicionado com a extremidade esquerda do círculo em$x=b, \, b>0,$ e seja girado em torno do$y$ eixo.

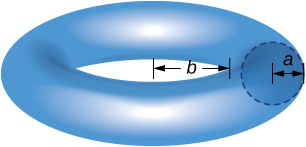
$Essa figura é um toro. Tem um raio interno de b. Dentro do toróide há uma seção transversal que é um círculo. O círculo tem raio a.$

Responda: Volume:$V = 2\pi^2a^2(b+a)$

41) Encontre o centro de massa$(\bar{x},\bar{y})$ de um fio fino ao longo do semicírculo$y=\sqrt{1−x^2}$ com massa unitária. (Dica: use o teorema de Pappus.)

Colaboradores

Template:ContribOpenStaxCalc