6.7: Integrais, funções exponenciais e logaritmos
- Page ID
- 187854
- Escreva a definição do logaritmo natural como integral.
- Reconheça a derivada do logaritmo natural.
- Integre funções que envolvem a função logarítmica natural.
- Defina o número\(e\) por meio de uma integral.
- Reconheça a derivada e a integral da função exponencial.
- Prove propriedades de logaritmos e funções exponenciais usando integrais.
- Expresse funções logarítmicas e exponenciais gerais em termos de logaritmos naturais e exponenciais.
Já examinamos funções exponenciais e logaritmos em capítulos anteriores. No entanto, abordamos alguns detalhes importantes nas discussões anteriores. Por exemplo, não estudamos como tratar funções exponenciais com expoentes irracionais. A definição do número e é outra área em que o desenvolvimento anterior estava um pouco incompleto. Agora temos as ferramentas para lidar com esses conceitos de uma forma matematicamente mais rigorosa, e fazemos isso nesta seção.
Para os fins desta seção, suponha que ainda não tenhamos definido o logaritmo natural, o número\(e\) ou qualquer uma das fórmulas de integração e diferenciação associadas a essas funções. No final da seção, teremos estudado esses conceitos de forma matematicamente rigorosa (e veremos que eles são consistentes com os conceitos que aprendemos anteriormente). Começamos a seção definindo o logaritmo natural em termos de uma integral. Essa definição forma a base da seção. A partir dessa definição, derivamos fórmulas de diferenciação, definimos o número\(e\) e expandimos esses conceitos para logaritmos e funções exponenciais de qualquer base.
O logaritmo natural como integral
Lembre-se da regra de potência para integrais:
\[ ∫ x^n \,dx = \dfrac{x^{n+1}}{n+1} + C , \quad n≠−1. \nonumber \]
Claramente, isso não funciona\(n=−1,\) quando nos forçaria a dividir por zero. Então, o que fazemos com\(\displaystyle ∫\dfrac{1}{x}\,dx\)? Lembre-se do Teorema Fundamental do Cálculo que\(\displaystyle ∫^x_1\dfrac{1}{t}dt\) é uma antiderivada de\(\dfrac{1}{x}.\) Portanto, podemos fazer a seguinte definição.
Para\(x>0\), defina a função logarítmica natural por
\[\ln x=∫^x_1\dfrac{1}{t}\,dt. \nonumber \]
Pois\(x>1\), essa é apenas a área abaixo\(y=\dfrac{1}{t}\) da curva\(1\) de\(x\) a. \(x<1\)Pois, nós temos
\[ ∫^x_1\dfrac{1}{t}\,dt=−∫^1_x\dfrac{1}{t}\,dt, \nonumber \]
então, neste caso, é o negativo da área sob a curva de\(x\) para\(1\) (veja a figura a seguir).
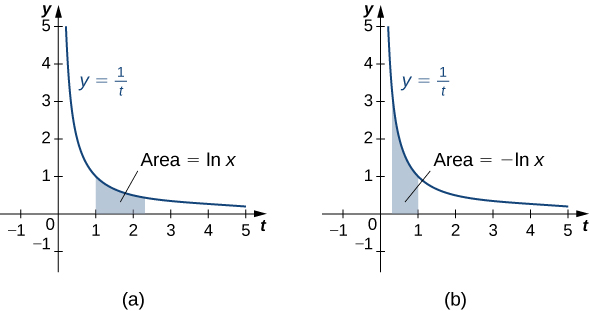
Observe isso\(\ln 1=0\). Além disso, a função\(y=\dfrac{1}{t}>0\) para\(x>0\). Portanto, pelas propriedades das integrais, fica claro que\(\ln x\) está aumentando para\(x>0\).
Propriedades do logaritmo natural
Devido à forma como definimos o logaritmo natural, a seguinte fórmula de diferenciação cai imediatamente como resultado do Teorema Fundamental do Cálculo.
Pois\(x>0\), a derivada do logaritmo natural é dada por
\[ \dfrac{d}{dx}\Big( \ln x \Big) = \dfrac{1}{x}. \nonumber \]
A função\(\ln x\) é diferenciável; portanto, é contínua.
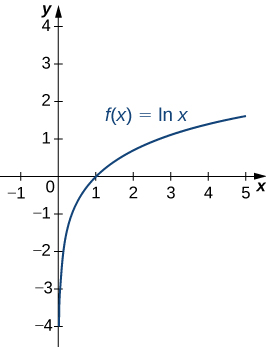
Um gráfico de\(\ln x\) é mostrado na Figura. Observe que ele é contínuo em todo o seu domínio de\((0,∞)\).
Calcule as seguintes derivadas:
- \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)\)
- \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)\)
Solução
Precisamos aplicar a regra da cadeia em ambos os casos.
- \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)=\dfrac{15x^2}{5x^3−2}\)
- \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)=\dfrac{2(\ln (3x))⋅3}{3x}=\dfrac{2(\ln (3x))}{x}\)
Calcule as seguintes derivadas:
- \(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)\)
- \(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)\)
- Dica
-
Aplique a fórmula de diferenciação que acabamos de fornecer e use a regra da cadeia conforme necessário.
- Responda
-
uma.\(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)=\dfrac{4x+1}{2x^2+x}\)
b.\(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)=\dfrac{6\ln (x^3)}{x}\)
Observe que, se usarmos a função de valor absoluto e criarmos uma nova função\(\ln |x|\), podemos estender o domínio do logaritmo natural para incluir\(x<0\). Então\(\dfrac{d}{dx}\Big( \ln x \Big)=\dfrac{1}{x}\). Isso dá origem à fórmula de integração familiar.
O logaritmo natural é a antiderivada da função\(f(u)=\dfrac{1}{u}\):
\[∫\dfrac{1}{u}\,du=\ln |u|+C. \nonumber \]
Calcule a integral\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx.\)
Solução
Usando\(u\) -substitution, let\(u=x^2+4\). Então,\(du=2x\,dx\) e nós temos
\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx=\dfrac{1}{2}∫\dfrac{1}{u}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln |x^2+4|+C=\dfrac{1}{2}\ln (x^2+4)+C.\)
Calcule a integral\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx.\)
- Dica
-
Aplique a fórmula de integração fornecida anteriormente e use a substituição u conforme necessário.
- Responda
-
\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx=\dfrac{1}{3}\ln ∣x^3+6∣+C\)
Embora tenhamos chamado nossa função de “logaritmo”, na verdade não provamos que nenhuma das propriedades dos logaritmos seja válida para essa função. Nós fazemos isso aqui.
Se\(a,\, b>0\) e\(r\) for um número racional, então
- \(\ln 1=0\)
- \(\ln (ab)=\ln a+\ln b\)
- \(\ln \left(\dfrac{a}{b}\right)=\ln a−\ln b\)
- \(\ln \left(a^r\right)=r\ln a\)
i. Por definição,\(\displaystyle \ln 1=∫^1_1\dfrac{1}{t}\,dt=0.\)
ii. Nós temos
\(\displaystyle \ln (ab)=∫^{ab}_1\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt.\)
Use\(u-substitution\) na última integral nesta expressão. Deixe\(u=t/a\). Então,\(du=(1/a)dt.\) além disso\(t=a,\, u=1\), quando e quando\(t=ab,\, u=b.\) Então nós temos
\(\displaystyle \ln (ab)=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_1\dfrac{a}{t}⋅\dfrac{1}{a}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^b_1\dfrac{1}{u}\,du=\ln a+\ln b.\)
iii. Note que
\(\dfrac{d}{dx}\Big(\ln (x^r)\Big)=\dfrac{rx^{r−1}}{x^r}=\dfrac{r}{x}\).
Além disso,
\(\dfrac{d}{dx}\Big((r\ln x)\Big)=\dfrac{r}{x}.\)
Como as derivadas dessas duas funções são as mesmas, pelo Teorema Fundamental do Cálculo, elas devem diferir por uma constante. Então, nós temos
\(\ln (x^r)=r\ln x+C\)
para alguma constante\(C\). Tomando\(x=1\), obtemos
\(\ln (1^r)=r\ln (1)+C\)
\(0=r(0)+C\)
\(C=0.\)
Assim\(\ln (x^r)=r\ln x\), a prova está completa. Observe que podemos estender essa propriedade para valores irracionais\(r\) posteriores nesta seção.
A parte iii. segue das partes ii. e iv. e a prova é deixada para você.
□
Use as propriedades dos logaritmos para simplificar a seguinte expressão em um único logaritmo:
\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right).\)
Solução
Nós temos
\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right)=\ln (3^2)−2 \ln 3+\ln (3^{−1})=2\ln 3−2\ln 3−\ln 3=−\ln 3.\)
Use as propriedades dos logaritmos para simplificar a seguinte expressão em um único logaritmo:
\( \ln 8−\ln 2−\ln \left(\tfrac{1}{4}\right)\)
- Dica
-
Aplique as propriedades dos logaritmos.
- Responda
-
\(4\ln 2\)
Definindo o número e
Agora que temos o logaritmo natural definido, podemos usar essa função para definir o número\(e\).
O número\(e\) é definido como sendo o número real, de forma que
\[\ln e=1\nonumber \]
Em outras palavras, a área abaixo da curva\(y=1/t\) entre\(t=1\) e\(t=e\) é\(1\) (Figura). A prova de que esse número existe e é único é deixada para você. (Dica: use o Teorema do Valor Intermediário para provar a existência e o fato de que\(\ln x\) está aumentando para provar a singularidade.)
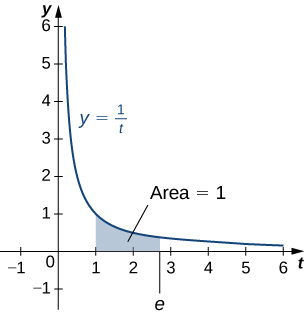
O número\(e\) pode ser mostrado irracional, embora não o façamos aqui (veja o Projeto Estudantil na Série Taylor e Maclaurin). Seu valor aproximado é dado por
\( e≈2.71828182846.\)
A função exponencial
Agora voltamos nossa atenção para a função\(e^x\). Observe que o logaritmo natural é um para um e, portanto, tem uma função inversa. Por enquanto, denotamos essa função inversa por\(\exp x\). Então,
\[ \exp(\ln x)=x \nonumber \]
para\(x>0\) e
\[ \ln (\exp x)=x \nonumber \]
para todos\(x\).
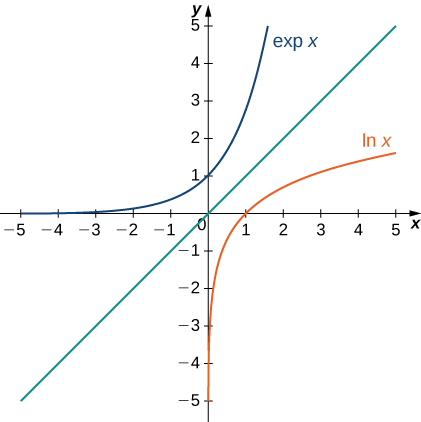
A figura a seguir mostra os gráficos de\(\exp x\)\(\ln x\) e.
Nós levantamos a hipótese de que\(\exp x=e^x\). Para valores racionais de\(x\), isso é fácil de mostrar. Se\(x\) é racional, então nós temos\(\ln (e^x)=x\ln e=x\). Assim, quando\(x\) é racional,\(e^x=\exp x\). Para valores irracionais de\(x\), simplesmente definimos\(e^x\) como a função inversa de\(\ln x\).
Para qualquer número real\(x\),\(y=e^x\) defina como sendo o número para o qual
\[\ln y=\ln (e^x)=x. \nonumber \]
Então temos\(e^x=\exp x\) para todos\(x\), e assim
\(e^{\ln x}=x\)para\(x>0\) e\(\ln (e^x)=x\)
para todos\(x\).
Propriedades da função exponencial
Como a função exponencial foi definida em termos de uma função inversa, e não em termos de uma potência de,\(e\) devemos verificar se as leis usuais dos expoentes são válidas para a função\(e^x\).
Se\(p\) e\(q\) forem números reais e\(r\) for um número racional, então
- \(e^pe^q=e^{p+q}\)
- \(\dfrac{e^p}{e^q}=e^{p−q}\)
- \((e^p)^r=e^{pr}\)
Observe que, se\(p\) e\(q\) forem racionais, as propriedades serão válidas. No entanto, se\(p\) ou\(q\) forem irracionais, devemos aplicar a definição da função inversa\(e^x\) e verificar as propriedades. Somente a primeira propriedade é verificada aqui; as outras duas são deixadas para você. Nós temos
\[ \ln (e^pe^q)=\ln (e^p)+\ln (eq)=p+q=\ln (e^{p+q}).\nonumber \]
Uma vez que\(\ln x\) é um para um, então
\[ e^pe^q=e^{p+q}.\nonumber \]
□
Como na parte iv. das propriedades do logaritmo, podemos estender a propriedade iii. para valores irracionais de\(r\), e fazemos isso até o final da seção.
Também queremos verificar a fórmula de diferenciação da função\(y=e^x\). Para fazer isso, precisamos usar a diferenciação implícita. Deixe\(y=e^x\). Então
\[ \begin{align*} \ln y &=x \\[5pt] \dfrac{d}{dx}\Big(\ln y\Big) &=\dfrac{d}{dx}\Big(x\Big) \\[5pt] \dfrac{1}{y}\dfrac{dy}{dx} &=1 \\[5pt] \dfrac{dy}{dx} &=y. \end{align*}\]
Assim, vemos
\[ \dfrac{d}{dx}\Big(e^x\Big)=e^x \nonumber \]
conforme desejado, o que leva imediatamente à fórmula de integração
\[ ∫e^x \,dx=e^x+C. \nonumber \]
Nós aplicamos essas fórmulas nos exemplos a seguir.
Avalie as seguintes derivadas:
- \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)\)
- \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)\)
Solução
Nós aplicamos a regra da cadeia conforme necessário.
- \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)=\dfrac{d}{dt}\Big(e^{3t+t^2}\Big)=e^{3t+t^2}(3+2t)\)
- \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)=e^{3x^2}6x\)
Avalie as seguintes derivadas:
- \(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)\)
- \(\dfrac{d}{dt}\Big((e^{2t})^3\Big)\)
- Dica
-
Use as propriedades das funções exponenciais e a regra da cadeia conforme necessário.
- Responda
-
uma.\(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)=e^{x^{2−5x}}(2x−5)\)
b.\(\dfrac{d}{dt}\Big((e^{2t})^3\Big)=6e^{6t}\)
Avalie a seguinte integral:\(\displaystyle ∫2xe^{−x^2}\,dx.\)
Solução
Usando\(u\) -substitution, let\(u=−x^2\). Então,\(du=−2x\,dx,\) e nós temos
\(\displaystyle ∫2xe^{−x^2}\,dx=−∫e^u\,du=−e^u+C=−e^{−x^2}+C.\)
Avalie a seguinte integral:\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx.\)
- Dica
-
Use as propriedades das funções exponenciais e\(u-substitution\) conforme necessário.
- Responda
-
\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx=−\dfrac{4}{3}e^{−3x}+C\)
Funções logarítmicas e exponenciais gerais
Fechamos esta seção examinando funções exponenciais e logaritmos com bases diferentes de\(e\). As funções exponenciais são funções da forma\(f(x)=a^x\). Observe que\(a=e\), a menos que, ainda não tenhamos uma definição matematicamente rigorosa dessas funções para expoentes irracionais. Vamos corrigir isso aqui definindo a função\(f(x)=a^x\) em termos da função exponencial\(e^x\). Em seguida, examinamos logaritmos com bases diferentes de e como funções inversas de funções exponenciais.
Para qualquer\(a>0,\) e para qualquer número real\(x\), defina da\(y=a^x\) seguinte forma:
\[y=a^x=e^{x \ln a}. \nonumber \]
Agora\(a^x\) é definido rigorosamente para todos os valores de\(x\). Essa definição também nos permite generalizar a propriedade iv. de logaritmos e a propriedade iii. de funções exponenciais para aplicar a valores racionais e irracionais de\(r\). É simples mostrar que as propriedades dos expoentes são válidas para funções exponenciais gerais definidas dessa maneira.
Agora, vamos aplicar essa definição para calcular uma fórmula de diferenciação para\(a^x\). Nós temos
\(\dfrac{d}{dx}\Big(a^x\Big)=\dfrac{d}{dx}\Big(e^{x\ln a}\Big)=e^{x\ln a}\ln a=a^x\ln a.\)
A fórmula de integração correspondente segue imediatamente.
Deixe\(a>0.\) então,
\[\dfrac{d}{dx}\Big(a^x\Big)=a^x \ln a \nonumber \]
e
\[∫a^x\,dx=\dfrac{1}{\ln a}a^x+C. \nonumber \]
Se\(a≠1\), então a função\(a^x\) é um para um e tem um inverso bem definido. Seu inverso é denotado por\(\log_a x\). Então,
\( y=\log_a x\)se e somente se\(x=a^y.\)
Observe que as funções logarítmicas gerais podem ser escritas em termos do logaritmo natural. Deixe\(y=\log_a x.\) então,\(x=a^y\). Tomando o logaritmo natural de ambos os lados dessa segunda equação, obtemos
\ [\ begin {align*}\ ln x &=\ ln (a^y)\\ [5pt]
\ ln x&=y\ ln a\\ [5pt]
y&=\ dfrac {\ ln x} {\ ln a}\\ [5pt]
\ log_a x&=\ dfrac {\ ln x} {\ ln a}. \ end {align*}\]
Assim, vemos que todas as funções logarítmicas são múltiplos constantes uma da outra. Em seguida, usamos essa fórmula para encontrar uma fórmula de diferenciação para um logaritmo com base\(a\). Mais uma vez, deixe\(y=\log_a x\). Então,
\ [\ begin {align*}\ dfrac {dy} {dx} &=\ dfrac {d} {dx}\ Big (\ log_a x\ Big)\\ [5pt]
&=\ dfrac {d} {dx}\ left (\ dfrac {\ ln x} {\ ln a}\ direita)\\ [5pt] & =(\ dfrac {\ ln x} {\ ln a}\ direita)\\ [5pt]
& =(\ dfrac {\ ln x} {\ ln a}\ direita)\\ [5pt] & =(\ dfrac {1} {\ ln a})\ dfrac {d} {dx}\ Big (\ ln x\ Big)\\ [5pt]
&=\ dfrac {1} {\ ln a} □\ dfrac {1} {x} =\ dfrac {1} {x\ ln a}\ end {align*}\]
Deixe\(a>0.\) então,
\[\dfrac{d}{dx}\Big(\log_a x\Big)=\dfrac{1}{x\ln a}. \nonumber \]
Avalie as seguintes derivadas:
- \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)\)
- \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)\)
Solução: precisamos aplicar a regra da cadeia conforme necessário.
- \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t}⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t+t^2}\Big)=2^{2t+t^2}\ln (2)(2+2t)\)
- \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)=\dfrac{1}{(7x^2+4)(\ln 8)}(14x)\)
Avalie as seguintes derivadas:
- \(\dfrac{d}{dt}\Big(4^{t^4}\Big)\)
- \(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)\)
- Dica
-
Use as fórmulas e aplique a regra da cadeia conforme necessário.
- Responda
-
uma.\(\dfrac{d}{dt}\Big(4^{t^4}\Big)=4^{t^4}(\ln 4)(4t^3)\)
b.\(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)=\dfrac{x}{(\ln 3)(x^2+1)}\)
Avalie a seguinte integral:\(\displaystyle ∫\dfrac{3}{2^{3x}}\,dx.\)
Solução
Use\(u-substitution\) e deixe\(u=−3x\). Então,\(du=−3\,dx\) e nós temos
\[ ∫\dfrac{3}{2^{3x}}\,dx=∫3⋅2^{−3x}\,dx=−∫2^u\,du=−\dfrac{1}{\ln 2}2^u+C=−\dfrac{1}{\ln 2}2^{−3x}+C.\nonumber \]
Avalie a seguinte integral:\(\displaystyle ∫x^2 2^{x^3}\,dx.\)
- Dica
-
Use as propriedades das funções exponenciais e da substituição u
- Responda
-
\(\displaystyle ∫x^2 2^{x^3}\,dx=\dfrac{1}{3\ln 2}2^{x^3}+C\)
Conceitos-chave
- O tratamento anterior de logaritmos e funções exponenciais não definiu as funções de forma precisa e formal. Esta seção desenvolve os conceitos de forma matematicamente rigorosa.
- A pedra angular do desenvolvimento é a definição do logaritmo natural em termos de uma integral.
- A função\(e^x\) é então definida como o inverso do logaritmo natural. As funções exponenciais gerais são definidas em termos de\(e^x\), e as funções inversas correspondentes são logaritmos gerais.
- As propriedades familiares dos logaritmos e expoentes ainda se mantêm nesse contexto mais rigoroso.
Equações-chave
- Função de logaritmo natural
- \(\displaystyle \ln x=∫^x_1\dfrac{1}{t}\,dt\)
- Função exponencial\(y=e^x\)
- \(\ln y=\ln (e^x)=x\)


