6.6: Momentos e centros de missa
- Page ID
- 187873
- Encontre o centro de massa dos objetos distribuídos ao longo de uma linha.
- Localize o centro de massa de uma placa fina.
- Use a simetria para ajudar a localizar o centróide de uma placa fina.
- Aplique o teorema de Pappus para o volume.
Nesta seção, consideramos centros de massa (também chamados de centróides, sob certas condições) e momentos. A ideia básica do centro de massa é a noção de ponto de equilíbrio. Muitos de nós já vimos artistas que giram placas nas pontas dos palitos. Os artistas tentam manter vários deles girando sem permitir que nenhum deles caia. Se olharmos para um único prato (sem girá-lo), há um ponto ideal no prato onde ele se equilibra perfeitamente no palito. Se colocarmos o palito em outro lugar que não seja aquele ponto ideal, o prato não se equilibra e cai no chão. (É por isso que os artistas giram as placas; a rotação ajuda a evitar que as placas caiam, mesmo que o bastão não esteja exatamente no lugar certo.) Matematicamente, esse ponto ideal é chamado de centro de massa da placa.
Nesta seção, primeiro examinamos esses conceitos em um contexto unidimensional e, em seguida, expandimos nosso desenvolvimento para considerar centros de massa de regiões bidimensionais e simetria. Por último, usamos centróides para determinar o volume de certos sólidos aplicando o teorema de Pappus.
Centro de Missa e Momentos
Vamos começar examinando o centro de massa em um contexto unidimensional. Considere um fio ou haste longo e fino de massa insignificante apoiado em um ponto de apoio, conforme mostrado na Figura\(\PageIndex{1a}\). Agora, suponha que coloquemos objetos com massas\(m_1\)\(d_1\) e\(m_2\)\(d_2\) distâncias e do fulcro, respectivamente, conforme mostrado na Figura\(\PageIndex{1b}\).
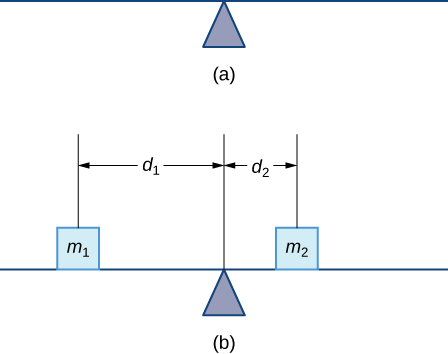
O exemplo real mais comum de um sistema como esse é uma gangorra de recreio, ou oscilante, com crianças de pesos diferentes sentadas a distâncias diferentes do centro. Em uma gangorra, se uma criança se senta em cada extremidade, a criança mais pesada afunda e a criança mais leve é levantada para o ar. No entanto, se a criança mais pesada deslizar em direção ao centro, a gangorra se equilibra. Aplicando esse conceito às massas na haste, notamos que as massas se equilibram se e somente se
\[m_1d_1=m_2d_2. \nonumber \]
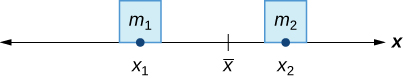
No exemplo da gangorra, equilibramos o sistema movendo as massas (crianças) em relação ao ponto de apoio. No entanto, estamos realmente interessados em sistemas nos quais as massas não podem se mover e, em vez disso, equilibramos o sistema movendo o ponto de apoio. Suponha que tenhamos duas massas pontuais\(m_1\) e\(m_2\), localizadas em uma reta numérica nos pontos\(x_1\) e\(x_2\), respectivamente (Figura\(\PageIndex{2}\)). O centro de massa,\(\bar{x}\), é o ponto em que o ponto de apoio deve ser colocado para equilibrar o sistema.
Assim, temos
\[ \begin{align*} m_1|x_1−\bar{x}| &=m_2|x_2−\bar{x}| \\[4pt] m_1(\bar{x}−x_1) &=m_2(x_2−\bar{x}) \\[4pt] m_1\bar{x}−m_1x_1 &=m_2x_2−m_2\bar{x} \\[4pt] \bar{x}(m_1+m_2) &=m_1x_1+m_2x_2 \end{align*} \nonumber \]
ou
\[ \bar{x} =\dfrac{m_1x_1+m_2x_2}{m_1+m_2} \label{COM} \]
A expressão no numerador da Equação\ ref {COM}\(m_1x_1+m_2x_2\),, é chamada de primeiro momento do sistema em relação à origem. Se o contexto for claro, geralmente descartamos a palavra primeiro e nos referimos a essa expressão como o momento do sistema. A expressão no denominador,\(m_1+m_2\), é a massa total do sistema. Assim, o centro de massa do sistema é o ponto em que a massa total do sistema pode ser concentrada sem alterar o momento.
Essa ideia não se limita apenas a massas de dois pontos. Em geral, se\(n\) as massas\(m_1,m_2,…,m_n,\) são colocadas em uma reta numérica em pontos,\(x_1,x_2,…,x_n,\) respectivamente, então o centro de massa do sistema é dado por
\[ \bar{x}=\dfrac{\displaystyle {\sum_{i=1}^nm_ix_i}}{\displaystyle {\sum_{i=1}^nm_i}} \nonumber \]
\(m_1,m_2,…,m_n\)Sejam massas pontuais colocadas em uma reta numérica em pontos\(x_1,x_2,…,x_n\), respectivamente, e\(\displaystyle m=\sum_{i=1}^nm_i\) denotem a massa total do sistema. Então, o momento do sistema em relação à origem é dado por
\[M=\sum_{i=1}^nm_ix_i \label{moment} \]
e o centro de massa do sistema é dado por
\[\bar{x}=\dfrac{M}{m}. \label{COM2a} \]
Nós aplicamos esse teorema no exemplo a seguir.
Suponha que massas de quatro pontos sejam colocadas em uma reta numérica da seguinte forma:
- \(m_1=30\,kg,\)colocado em\(x_1=−2m\)
- \(m_2=5\,kg,\)colocado em\(x_2=3m\)
- \(m_3=10\,kg,\)colocado em\(x_3=6m\)
- \(m_4=15\,kg,\)colocado em\(x_4=−3m.\)
Solução
Encontre o momento do sistema em relação à origem e encontre o centro de massa do sistema.
Primeiro, precisamos calcular o momento do sistema (Equação\ ref {momento}):
\[ \begin{align*} M &=\sum_{i=1}^4m_ix_i \\[4pt] &= −60+15+60−45 \\[4pt] &=−30. \end{align*}\]
Agora, para encontrar o centro de massa, precisamos da massa total do sistema:
\[ \begin{align*} m &=\sum_{i=1}^4m_i \\[4pt] &=30+5+10+15 \\[4pt] &= 60\, kg \end{align*}\]
Então temos (da Equação\ ref {Com2a})
\(\bar{x}–=\dfrac{M}{m}=−\dfrac{30}{60}=−\dfrac{1}{2}\).
O centro de massa está localizado a 1/2 m à esquerda da origem.
Suponha que massas de quatro pontos sejam colocadas em uma reta numérica da seguinte forma:
- \(m_1=12\,kg\)colocado em\(x_1=−4m\)
- \(m_2=12\,kg\)colocado em\(x_2=4m\)
- \(m_3=30\,kg\)colocado em\(x_3=2m\)
- \(m_4=6\,kg,\)colocado em\(x_4=−6m.\)
Encontre o momento do sistema em relação à origem e encontre o centro de massa do sistema.
- Dica
-
Use o processo do exemplo anterior.
- Responda
-
\(M=24,\bar{x}=\dfrac{2}{5}m\)
Podemos generalizar esse conceito para encontrar o centro de massa de um sistema de massas pontuais em um plano. \(m_1\)Seja uma massa pontual localizada em um ponto\((x_1,y_1)\) do plano. Então, o momento\(M_x\) da massa em relação ao\(x\) eixo -é dado por\(M_x=m_1y_1\). Da mesma forma, o momento em\(M_y\) relação ao\(y\) eixo -é dado por
\[M_y=m_1x_1. \nonumber \]
Observe que a\(x\) coordenada -do ponto é usada para calcular o momento em relação ao\(y\) eixo -e vice-versa. A razão é que a\(x\) coordenada -fornece a distância da massa do ponto até o\(y\) eixo -, e a\(y\) coordenada -fornece a distância até o\(x\) eixo -( veja a figura a seguir).

Se tivermos várias massas de pontos no\(xy\) plano -, podemos usar os momentos em relação aos\(y\) eixos\(x\) - e -para calcular as\(y\) coordenadas\(x\) - e -do centro de massa do sistema.
\(m_1\)Sejam,,...,\(m_n\) massas pontuais localizadas no\(xy\) plano -em pontos\((x_1,y_1),(x_2,y_2),…,(x_n,y_n),\) respectivamente e\(\displaystyle m=\sum_{i=1}^nm_i\) denotem a massa total do sistema.\(m_2\) Em seguida, os momentos\(M_x\) e\(M_y\) do sistema em relação aos\(y\) eixos\(x\) - e -, respectivamente, são dados por
\[M_x=\sum_{i=1}^nm_iy_i \label{COM1} \]
e
\[M_y=\sum_{i=1}^nm_ix_i. \label{COM2} \]
Além disso, as coordenadas do centro de massa\((\bar{x},\bar{y})\) do sistema são
\[\bar{x}=\dfrac{M_y}{m} \label{COM3} \]
e
\[\bar{y}=\dfrac{M_x}{m}. \label{COM4} \]
O próximo exemplo demonstra como as fórmulas do centro de massa (Equações\ ref {COM1} -\ ref {COM4}) podem ser aplicadas.
Suponha que massas de três pontos sejam colocadas no\(xy\) plano -da seguinte forma (suponha que as coordenadas sejam dadas em metros):
- \(m_1=2\,kg\)colocado em\((−1,3),\)
- \(m_2=6\,kg\)colocado em\((1,1),\)
- \(m_3=4\,kg\)colocado em\((2,−2).\)
Encontre o centro de massa do sistema.
Solução
Primeiro, calculamos a massa total do sistema:
\[m=\sum_{i=1}^3m_i=2+6+4=12\,kg. \nonumber \]
A seguir, encontramos os momentos com relação aos\(y\) eixos\(x\) - e -:
\[\begin{align*} M_y &=\sum_{i=1}^3m_ix_i=−2+6+8=12, \\[4pt] M_x &=\sum_{i=1}^3m_iy_i=6+6−8=4. \end{align*}\]
Então nós temos
\[\bar{x}=\dfrac{M_y}{m}=\dfrac{12}{12}=1 \nonumber \]
e
\[\bar{y}=\dfrac{M_x}{m}=\dfrac{4}{12}=\dfrac{1}{3}. \nonumber \]
O centro de massa do sistema está\((1,1/3),\) em metros.
Suponha que massas de três pontos sejam colocadas em uma reta numérica da seguinte forma (suponha que as coordenadas sejam dadas em metros):
- \(m_1=5\,kg,\)colocado em\((−2,−3),\)
- \(m_2=3\, kg,\)colocado em\((2,3),\)
- \(m_3=2\, kg,\)colocado em\((−3,−2).\)
Encontre o centro de massa do sistema.
- Dica
-
Use o processo do exemplo anterior.
- Responda
-
\((−1,−1)\)m
Centro de massa de placas finas
Até agora, analisamos sistemas de massas de pontos em uma linha e em um plano. Agora, em vez de ter a massa de um sistema concentrada em pontos discretos, queremos observar sistemas nos quais a massa do sistema é distribuída continuamente por uma fina camada de material. Para nossos propósitos, assumimos que a folha é fina o suficiente para ser tratada como se fosse bidimensional. Essa folha é chamada de lâmina. Em seguida, desenvolvemos técnicas para encontrar o centro de massa de uma lâmina. Nesta seção, também assumimos que a densidade da lâmina é constante.
As lâminas são frequentemente representadas por uma região bidimensional em um plano. O centro geométrico dessa região é chamado de centróide. Como assumimos que a densidade da lâmina é constante, o centro de massa da lâmina depende apenas da forma da região correspondente no plano; não depende da densidade. Nesse caso, o centro de massa da lâmina corresponde ao centróide da região delineada no plano. Assim como nos sistemas de massas pontuais, precisamos encontrar a massa total da lâmina, bem como os momentos da lâmina em relação aos\(y\) eixos\(x\) - e.
Primeiro, consideramos uma lâmina na forma de um retângulo. Lembre-se de que o centro de massa de uma lâmina é o ponto onde a lâmina se equilibra. Para um retângulo, esse ponto é o centro horizontal e vertical do retângulo. Com base nesse entendimento, fica claro que o centro de massa de uma lâmina retangular é o ponto onde as diagonais se cruzam, o que é resultado do princípio da simetria, e isso é declarado aqui sem prova.
Se uma região\(R\) é simétrica em relação a uma linha\(l\), então o centróide de\(R\) está ligado\(l\).
Vamos nos voltar para lâminas mais gerais. Suponha que tenhamos uma lâmina delimitada acima pelo gráfico de uma função contínua\(f(x)\), abaixo pelo\(x\) eixo -e à esquerda e à direita pelas linhas\(x=a\) e\(x=b\), respectivamente, conforme mostrado na figura a seguir.
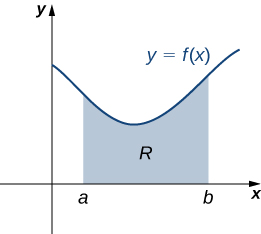
Assim como nos sistemas de massas pontuais, para encontrar o centro de massa da lâmina, precisamos encontrar a massa total da lâmina, bem como os momentos da lâmina em relação aos\(y\) eixos\(x\) - e. Como fizemos muitas vezes antes, aproximamos essas quantidades dividindo o intervalo\([a,b]\) e construindo retângulos.
\(i=0,1,2,…,n,\)Pois\(P={x_i}\) seja uma partição regular de\([a,b]\). Lembre-se de que podemos escolher qualquer ponto dentro do intervalo\([x_{i−1},x_i]\) como nosso\(x^∗_i\). Nesse caso, queremos ser\(x^∗_i\) a coordenada x do centróide de nossos retângulos. Assim, para\(i=1,2,…,n\), selecionamos\(x^∗_i∈[x_{i−1},x_i]\) tal que\(x^∗_i\) seja o ponto médio do intervalo. Isso é,\(x^∗_i=(x_{i−1}+x_i)/2\). Agora, para\(i=1,2,…,n,\) construir um retângulo de altura\(f(x^∗_i)\) em\([x_{i−1},x_i].\) O centro de massa desse retângulo é\((x^∗_i,(f(x^∗_i))/2),\) mostrado na figura a seguir.
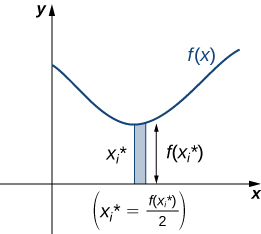
Em seguida, precisamos encontrar a massa total do retângulo. Vamos\(ρ\) representar a densidade da lâmina (note que\(ρ\) é uma constante). Neste caso,\(ρ\) é expresso em termos de massa por unidade de área. Assim, para encontrar a massa total do retângulo, multiplicamos a área do retângulo por\(ρ\). Então, a massa do retângulo é dada por\(ρf(x^∗_i)Δx\).
Para obter a massa aproximada da lâmina, adicionamos as massas de todos os retângulos para obter
\[m≈\sum_{i=1}^nρf(x^∗_i)Δx. \label{eq51} \]
A equação\ ref {eq51} é uma soma de Riemann. Tomando o limite\(n→∞\) conforme a massa exata da lâmina:
\[ \begin{align*} m &=\lim_{n→∞}\sum_{i=1}^nρf(x^∗_i)Δx \\[4pt] &=ρ∫^b_af(x)dx. \end{align*}\]
Em seguida, calculamos o momento da lâmina em relação ao eixo x. Voltando ao retângulo representativo, lembre-se de que seu centro de massa é\((x^∗_i,(f(x^∗_i))/2)\). Lembre-se também de que tratar o retângulo como se fosse uma massa pontual localizada no centro da massa não muda o momento. Assim, o momento do retângulo em relação ao eixo x é dado pela massa do retângulo\(ρf(x^∗_i)Δx\), multiplicado pela distância do centro de massa ao eixo x:\((f(x^∗_i))/2\). Portanto, o momento em relação ao eixo x do retângulo é\(ρ([f(x^∗_i)]^2/2)Δx.\) Somando os momentos dos retângulos e tomando o limite da soma de Riemann resultante, vemos que o momento da lâmina em relação ao eixo x é
\[ \begin{align*}M_x &=\lim_{n→∞}\sum_{i=1}^nρ\dfrac{[f(x^∗_i)]^2}{2}Δx \\[4pt] &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx.\end{align*}\]
Derivamos o momento em relação ao eixo y da mesma forma, observando que a distância do centro de massa do retângulo ao eixo y é\(x^∗_i\). Então, o momento da lâmina em relação ao eixo y é dado por
\[ \begin{align*}M_y &=\lim_{n→∞}\sum_{i=1}^nρx^∗_if(x^∗)i)Δx\\[4pt] &=ρ∫^b_axf(x)dx.\end{align*}\]
Encontramos as coordenadas do centro de massa dividindo os momentos pela massa total para dar\(\bar{x}=M_y/m\)\(\bar{y}=M_x/m\) e. Se observarmos atentamente as expressões para e\(M_x,M_y\)\(m\), perceberemos que a constante é\(ρ\) cancelada quando\(\bar{x}\) e\(\bar{y}\) é calculada.
Resumimos essas descobertas no seguinte teorema.
Seja R denotar uma região delimitada acima pelo gráfico de uma função contínua\(f(x)\), abaixo pelo eixo x e à esquerda e à direita pelas linhas\(x=a\) e\(x=b\), respectivamente. Vamos\(ρ\) indicar a densidade da lâmina associada. Em seguida, podemos fazer as seguintes declarações:
- A massa da lâmina é\[m=ρ∫^b_af(x)dx. \label{eq4a} \]
- Os momentos\(M_x\) e\(M_y\) da lâmina em relação aos eixos x e y, respectivamente, são\[M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx\label{eq4b} \] e\[M_y=ρ∫^b_axf(x)dx.\label{eq4c} \]
- As coordenadas do centro de massa\((\bar{x},\bar{y})\) são\[\bar{x}=\dfrac{M_y}{m} \label{eq4d} \] e\[\bar{y}=\dfrac{M_x}{m}. \label{eq4e} \]
No próximo exemplo, usamos esse teorema para encontrar o centro de massa de uma lâmina.
Seja R a região delimitada acima pelo gráfico da função\(f(x)=\sqrt{x}\) e abaixo pelo eixo x no intervalo\([0,4]\). Encontre o centróide da região.
Solução
A região é mostrada na figura a seguir.
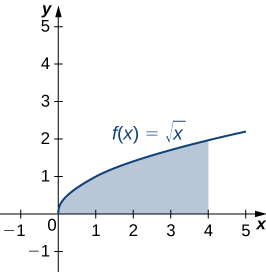
Como nos pedem apenas o centróide da região, em vez da massa ou dos momentos da lâmina associada, sabemos que a constante de densidade acaba sendo\(ρ\) cancelada dos cálculos. Portanto, por uma questão de conveniência, vamos supor\(ρ=1\).
Primeiro, precisamos calcular a massa total (Equação\ ref {eq4a}):
\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^4_0\sqrt{x}dx \\[4pt] &=\dfrac{2}{3}x^{3/2}∣^4_0 \\[4pt] &=\dfrac{2}{3}[8−0] \\[4pt] &=\dfrac{16}{3}. \end{align*}\]
Em seguida, calculamos os momentos (Equação\ ref {eq4d}):
\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=∫^4_0\dfrac{x}{2}dx \\[4pt] &=\dfrac{1}{4}x^2∣^4_0 \\[4pt] &=4 \end{align*}\]
e (Equação\ ref {eq4c}):
\[ \begin{align*} M_y &=ρ∫^b_axf(x)dx \\[4pt] &=∫^4_0x\sqrt{x}dx \\[4pt] &=∫^4_0x^{3/2}dx \\[4pt] &=\dfrac{2}{5}x^{5/2}∣^4_0 \\[4pt] &=\dfrac{2}{5}[32−0] \\[4pt] &=\dfrac{64}{5}. \end{align*}\]
Assim, temos (Equação\ ref {eq4d}):
\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m} \\[4pt] &=\dfrac{64/5}{16/3} \\[4pt] &=\dfrac{64}{5}⋅\dfrac{3}{16} \\[4pt] &=\dfrac{12}{5} \end{align*}\]
e (Equação\ ref {eq4e}):
\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y} \\[4pt] &=\dfrac{4}{16/3} \\[4pt] &=4⋅\dfrac{3}{16} \\[4pt] &=\dfrac{3}{4}. \end{align*}\]
O centróide da região é\((12/5,3/4).\)
\(R\)Seja a região delimitada acima pelo gráfico da função\(f(x)=x^2\) e abaixo pelo eixo x no intervalo\([0,2].\) Encontre o centróide da região.
- Dica
-
Use o processo do exemplo anterior.
- Responda
-
O centróide da região é\((3/2,6/5).\)
Também podemos adaptar essa abordagem para encontrar centróides de regiões mais complexas. Suponha que nossa região seja limitada acima pelo gráfico de uma função contínua\(f(x)\), como antes, mas agora, em vez de ter o limite inferior da região no eixo x, suponha que a região esteja limitada abaixo pelo gráfico de uma segunda função contínua\(g(x)\), conforme mostrado na Figura\(\PageIndex{7}\).
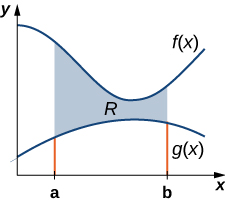
Novamente, dividimos o intervalo\([a,b]\) e construímos retângulos. Um retângulo representativo é mostrado na Figura\(\PageIndex{8}\).
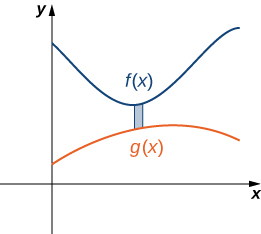
Observe que o centróide desse retângulo é\((x^∗_i,(f(x^∗_i)+g(x^∗_i))/2)\). Não abordaremos todos os detalhes do desenvolvimento da soma de Riemann, mas vamos dar uma olhada em algumas das principais etapas. No desenvolvimento das fórmulas para a massa da lâmina e o momento em relação ao eixo y, a altura de cada retângulo é dada por\(f(x^∗_i)−g(x^∗_i)\), o que leva à expressão\(f(x)−g(x)\) nos integrandos.
No desenvolvimento da fórmula para o momento em relação ao eixo x, o momento de cada retângulo é encontrado multiplicando a área do retângulo,\(ρ[f(x^∗_i)−g(x^∗_i)]Δx,\) pela distância do centróide do\(x\) eixo -,\((f(x^∗_i)+g(x^∗_i))/2\), o que dá\(ρ(1/2){[f(x^∗_i)]^2−[g(x^∗_i)]^2}Δx\). Resumindo essas descobertas, chegamos ao seguinte teorema.
Vamos\(R\) denotar uma região limitada acima pelo gráfico de uma função contínua\(f(x),\) abaixo pelo gráfico da função contínua\(g(x)\), e à esquerda e à direita pelas linhas\(x=a\) e\(x=b\), respectivamente. Vamos\(ρ\) indicar a densidade da lâmina associada. Em seguida, podemos fazer as seguintes declarações:
- A massa da lâmina é\[m=ρ∫^b_a[f(x)−g(x)]dx. \nonumber \]
- Os momentos\(M_x\) e\(M_y\) da lâmina em relação aos eixos x e y, respectivamente, são\[M_x=ρ∫^b_a12([f(x)]^2−[g(x)]^2)dx \nonumber \] e\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
- As coordenadas do centro de massa\(\bar{x},\bar{y})\) são\[\bar{x}=\dfrac{M_y}{m} \nonumber \] e\[\bar{y}=\dfrac{M_x}{m} \nonumber \]
Ilustramos esse teorema no exemplo a seguir.
Seja R a região delimitada acima pelo gráfico da função\(f(x)=1−x^2\) e abaixo pelo gráfico da função\(g(x)=x−1.\) Encontre o centróide da região.
Solução
A região é mostrada na figura a seguir.
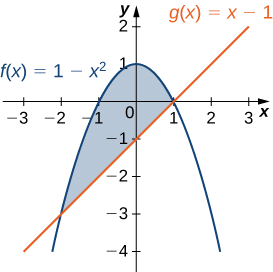
Os gráficos das funções se cruzam em\((−2,−3)\) e\((1,0)\), então integramos de −2 a 1. Mais uma vez, por uma questão de conveniência, suponha\(ρ=1\).
Primeiro, precisamos calcular a massa total:
\[ \begin{align*} m &=ρ∫^b_a[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}[1−x^2−(x−1)]dx \\[4pt] &=∫^1_{−2}(2−x^2−x)dx \\[4pt] &=\left[2x−\dfrac{1}{3}x^3−\dfrac{1}{2}x^2\right]∣^1_{−2} \\[4pt] &=\left[2−\dfrac{1}{3}−\dfrac{1}{2}\right]−\left[−4+\dfrac{8}{3}−2\right]\\[4pt] &=\dfrac{9}{2}. \end{align*}\]
Em seguida, calculamos os momentos:
\[ \begin{align*} M_x&=ρ∫^b_a\dfrac{1}{2}([f(x)]^2−[g(x)]^2)dx \\[4pt] &=\dfrac{1}{2}∫^1_{−2}((1−x^2)^2−(x−1)^2)dx\\[4pt] &=\dfrac{1}{2}∫^1_{−2}(x^4−3x^2+2x)dx \\[4pt] &=\dfrac{1}{2} \left[\dfrac{x^5}{5}−x^3+x^2\right]∣^1_{−2}\\[4pt] &=−\dfrac{27}{10} \end{align*}\]
e
\[ \begin{align*} M_y &=ρ∫^b_ax[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}x[(1−x^2)−(x−1)]dx\\[4pt] &=∫^1_{−2}x[2−x^2−x]dx\\[4pt] &=∫^1_{−2}(2x−x^4−x^2)dx \\[4pt] &=\left[x^2−\dfrac{x^5}{5}−\dfrac{x^3}{3}\right]∣^1_{−2}\\[4pt] &=−\dfrac{9}{4}. \end{align*}\]
Portanto, temos
\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m}\\[4pt] &=−\dfrac{9}{4}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{1}{2} \end{align*}\]
e
\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y}\\[4pt] &=−\dfrac{27}{10}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{3}{5}. \end{align*}\]
O centróide da região é\((−(1/2),−(3/5)).\)
\(R\)Seja a região delimitada acima pelo gráfico da função\(f(x)=6−x^2\) e abaixo pelo gráfico da função\(g(x)=3−2x.\) Encontre o centróide da região.
- Dica
-
Use o processo do exemplo anterior.
- Responda
-
O centróide da região é\((1,13/5).\)
O princípio da simetria
Declaramos o princípio de simetria anteriormente, quando observávamos o centróide de um retângulo. O princípio de simetria pode ser uma grande ajuda ao encontrar centróides de regiões simétricas. Considere o exemplo a seguir.
Seja R a região delimitada acima pelo gráfico da função\(f(x)=4−x^2\) e abaixo pelo eixo x. Encontre o centróide da região.
Solução
A região é representada na figura a seguir
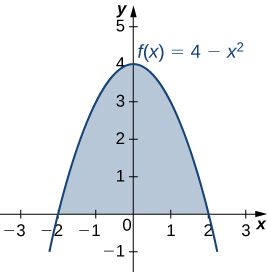
A região é simétrica em relação ao eixo y. Portanto, a coordenada x do centróide é zero. Só precisamos calcular\(\bar{y}\). Mais uma vez, por uma questão de conveniência, suponha\(ρ=1\).
Primeiro, calculamos a massa total:
\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^2_{−2}(4−x^2)dx \\[4pt] &=\left[4x−\dfrac{x^3}{3}\right]∣^2_{−2} \\[4pt] &=\dfrac{32}{3}. \end{align*}\]
Em seguida, calculamos os momentos. Só precisamos de\(M_x\):
\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=\dfrac{1}{2}∫^2_{−2}\left[4−x^2\right]^2dx =\dfrac{1}{2}∫^2_{−2}(16−8x^2+x^4)dx \\[4pt] &=\dfrac{1}{2}\left[\dfrac{x^5}{5}−\dfrac{8x^3}{3}+16x\right]∣^2_{−2}=\dfrac{256}{15} \end{align*}\]
Então nós temos
\[\bar{y}=\dfrac{M_x}{y}=\dfrac{256}{15}⋅\dfrac{3}{32}=\dfrac{8}{5}. \nonumber \]
O centróide da região é\((0,8/5).\)
\(R\)Seja a região delimitada acima pelo gráfico da função\(f(x)=1−x^2\) e abaixo\(x\) pelo eixo. Encontre o centróide da região.
- Dica
-
Use o processo do exemplo anterior.
- Responda
-
O centróide da região é\((0,2/5).\)
O Grand Canyon Skywalk foi aberto ao público em 28 de março de 2007. Essa maravilha da engenharia é uma plataforma de observação em forma de ferradura suspensa 4000 pés acima do Rio Colorado, na margem oeste do Grand Canyon. Seu piso de vidro cristalino permite vistas deslumbrantes do cânion abaixo (veja a figura a seguir).

O Skywalk é um design cantilever, o que significa que a plataforma de observação se estende sobre a borda do cânion, sem meios visíveis de apoio abaixo dela. Apesar da falta de postes de apoio ou escoras visíveis, as estruturas cantilever são projetadas para serem muito estáveis e o Skywalk não é exceção. A plataforma de observação está firmemente presa a postes de apoio que se estendem 46 pés até o leito rochoso. A estrutura foi construída para suportar ventos de 100 mph e um terremoto de magnitude 8,0 dentro de 50 milhas e é capaz de suportar mais de 70.000.000 lb.
Um fator que afeta a estabilidade do Skywalk é o centro de gravidade da estrutura. Vamos calcular o centro de gravidade do Skywalk e examinar como o centro de gravidade muda quando os turistas saem para a plataforma de observação.
A plataforma de observação é em forma de U. As pernas do U têm 10 pés de largura e começam em terra, sob o centro de visitantes, a 48 pés da borda do cânion. A plataforma se estende 70 pés sobre a borda do cânion.
Para calcular o centro de massa da estrutura, nós a tratamos como uma lâmina e usamos uma região bidimensional no plano xy para representar a plataforma. Começamos dividindo a região em três sub-regiões para que possamos considerar cada sub-região separadamente. A primeira região, indicada\(R_1\), consiste na parte curva do U. Nós modelamos\(R_1\) como um anel semicircular, com raio interno de 25 pés e raio externo de 35 pés, centrado na origem (Figura\(\PageIndex{12}\)).
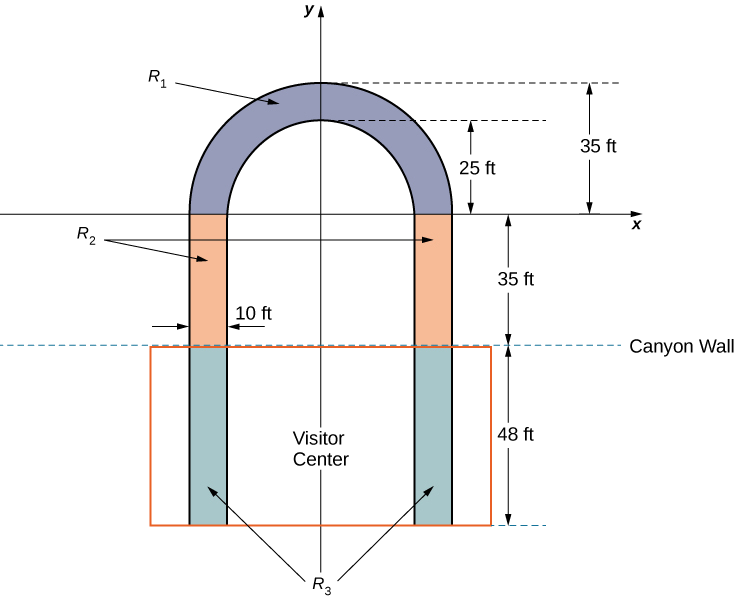
As pernas da plataforma, estendendo-se 35 pés entre elas\(R_1\) e a parede do cânion, compõem a segunda sub-região,\(R_2\). Por último, as extremidades das pernas, que se estendem 48 pés abaixo do centro de visitantes, compreendem a terceira sub-região,\(R_3\). Suponha que a densidade da lâmina seja constante e suponha que o peso total da plataforma seja de 1.200.000 libras (sem incluir o peso do centro de visitantes; consideraremos isso mais tarde). Use\(g=32\;ft/sec^2\).
- Calcule a área de cada uma das três sub-regiões. Observe que as áreas das regiões\(R_2\)\(R_3\) devem incluir apenas as áreas das pernas, não o espaço aberto entre elas. Arredonde as respostas para o pé quadrado mais próximo.
- Determine a massa associada a cada uma das três sub-regiões.
- Calcule o centro de massa de cada uma das três sub-regiões.
- Agora, trate cada uma das três sub-regiões como uma massa pontual localizada no centro de massa da sub-região correspondente. Usando essa representação, calcule o centro de massa de toda a plataforma.
- Suponha que o centro de visitantes pese 2.200.000 libras, com um centro de massa correspondente ao centro de massa de\(R_3\) .Tratando o centro de visitantes como uma massa pontual, recalcule o centro de massa do sistema. Como o centro de massa muda?
- Embora o Skywalk tenha sido construído para limitar o número de pessoas na plataforma de observação a 120, a plataforma é capaz de suportar até 800 pessoas pesando 200 libras cada. Se todas as 800 pessoas pudessem entrar na plataforma e todas elas fossem para a extremidade mais distante da plataforma, como o centro de gravidade do sistema seria afetado? (Inclua o centro de visitantes nos cálculos e represente as pessoas por uma massa de pontos localizada na borda mais distante da plataforma, a 70 pés da parede do cânion.)
Teorema de Pappus
Esta seção termina com uma discussão sobre o teorema de Pappus para volume, que nos permite encontrar o volume de tipos específicos de sólidos usando o centróide. (Também existe um teorema de Pappus para área de superfície, mas é muito menos útil do que o teorema para volume.)
\(R\)Seja uma região no plano e seja l uma linha no plano que não se cruza\(R\). Então, o volume do sólido de revolução formado pela rotação\(R\) em torno de l é igual à área de\(R\) multiplicada pela distância d percorrida pelo centróide de\(R\).
Podemos provar o caso quando a região é limitada acima pelo gráfico de uma função\(f(x)\) e abaixo pelo gráfico de uma função em um\(g(x)\) intervalo\([a,b]\), e para a qual o eixo de revolução é o\(y\) eixo. Nesse caso, a área da região é\(\displaystyle A=∫^b_a[f(x)−g(x)]\,dx\). Como o eixo de rotação é o\(y\) eixo -, a distância percorrida pelo centróide da região depende apenas da\(x\) coordenada -do centróide,\(\bar{x}\), que é
\[x=\dfrac{M_y}{m}, \nonumber \]
onde
\[m=ρ∫^b_a[f(x)−g(x)]dx \nonumber \]
e
\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Então,
\[d=2π\dfrac{\displaystyle {ρ∫^b_ax[f(x)−g(x)]dx}}{\displaystyle{ρ∫^b_a[f(x)−g(x)]dx}} \nonumber \]
e, portanto,
\[d⋅A=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]
No entanto, usando o método de conchas cilíndricas, temos
\[V=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Então,
\[V=d⋅A \nonumber \]
e a prova está completa.
□
\(R\)Seja um círculo de raio 2 centrado em\((4,0).\) Use o teorema de Pappus para volume para encontrar o volume do toróide gerado pela rotação\(R\) em torno do\(y\) eixo.
Solução
A região e o toro estão representados na figura a seguir.
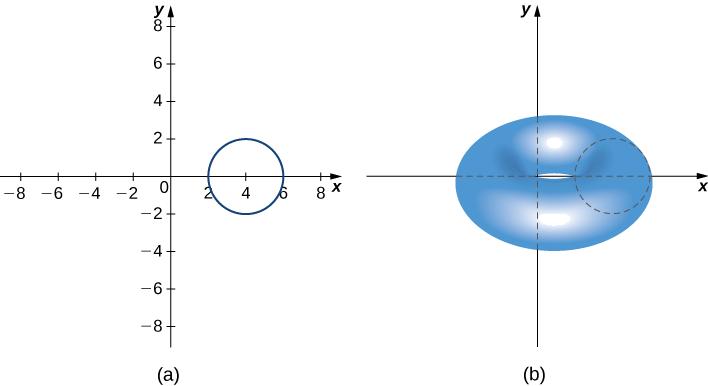
A região\(R\) é um círculo de raio 2, então a área de R é\(A=4π\;\text{units}^2\). Pelo princípio da simetria, o centróide de R é o centro do círculo. O centróide viaja ao redor do\(y\) eixo -em um caminho circular de raio 4, então o centróide viaja\(d=8π\) unidades. Então, o volume do toróide é de\(A⋅d=32π^2\) unidades 3.
Seja R um círculo de raio 1 centrado em\((3,0).\) Use o teorema de Pappus para volume para encontrar o volume do toróide gerado pela rotação\(y\) de R em torno do eixo.
- Dica
-
Use o processo do exemplo anterior.
- Responda
-
\(6π^2\)unidades 3
Conceitos-chave
- Matematicamente, o centro de massa de um sistema é o ponto em que a massa total do sistema pode ser concentrada sem alterar o momento. Falando vagamente, o centro de massa pode ser considerado o ponto de equilíbrio do sistema.
- Para massas de pontos distribuídas ao longo de uma reta numérica, o momento do sistema em relação à origem é\(\displaystyle M=\sum^n_{i=1}m_ix_i.\) Para massas de pontos distribuídas em um plano, os momentos do sistema em relação aos\(y\) eixos\(x\) - e -, respectivamente, são\(\displaystyle M_x=\sum^n_{i=1}m_iy_i\) e\(\displaystyle M_y=\sum^n_{i=}m_ix_i\), respectivamente.
- Para uma lâmina delimitada acima por uma função\(f(x)\), os momentos do sistema em relação aos\(y\) eixos\(x\) - e -, respectivamente, são\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) e\(\displaystyle M_y=ρ∫^b_axf(x)\,dx.\)
- As\(y\) coordenadas\(x\) - e -do centro de massa podem ser encontradas dividindo os momentos ao redor do\(y\) eixo -e ao redor do\(x\) eixo -, respectivamente, pela massa total. O princípio da simetria diz que se uma região é simétrica em relação a uma linha, o centróide da região está na linha.
- O teorema de Pappus para volume diz que se uma região é girada em torno de um eixo externo, o volume do sólido resultante é igual à área da região multiplicada pela distância percorrida pelo centróide da região.
Equações-chave
- Massa de uma lâmina
\(\displaystyle m=ρ∫^b_af(x)dx\)
- Momentos de uma lâmina
\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\text{ and }M_y=ρ∫^b_axf(x)\,dx\)
- Centro de massa de uma lâmina
\(\bar{x}=\dfrac{M_y}{m}\text{ and }\bar{y}=\dfrac{M_x}{m}\)
Glossário
- centro de massa
- o ponto em que a massa total do sistema poderia ser concentrada sem alterar o momento
- centróide
- o centróide de uma região é o centro geométrico da região; as lâminas são frequentemente representadas por regiões no plano; se a lâmina tiver uma densidade constante, o centro de massa da lâmina depende apenas da forma da região planar correspondente; nesse caso, o centro de massa da lâmina corresponde a o centróide da região representativa
- lâmina
- uma fina folha de material; as lâminas são finas o suficiente para que, para fins matemáticos, possam ser tratadas como se fossem bidimensionais
- momento
- se n massas estiverem dispostas em uma reta numérica, o momento do sistema em relação à origem é dado por\(\displaystyle M=\sum^n_{i=1}m_ix_i\); se, em vez disso, considerarmos uma região no plano, limitada acima por uma função\(f(x)\) ao longo de um intervalo\([a,b]\), então os momentos da região em relação ao\(x\) - e \(y\)-eixos são dados por\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) e\(\displaystyle M_y=ρ∫^b_axf(x)\,dx\), respectivamente
- princípio de simetria
- o princípio de simetria afirma que se uma região\(R\) é simétrica em relação a uma linha\(I\), então o centróide de\(R\) está em\(I\)
- teorema de Pappus para volume
- esse teorema afirma que o volume de um sólido de revolução formado pela rotação de uma região em torno de um eixo externo é igual à área da região multiplicada pela distância percorrida pelo centróide da região


