6.5: Aplicações físicas da integração
- Page ID
- 187824
- Determine a massa de um objeto unidimensional a partir de sua função de densidade linear.
- Determine a massa de um objeto circular bidimensional a partir de sua função de densidade radial.
- Calcule o trabalho realizado por uma força variável atuando ao longo de uma linha.
- Calcule o trabalho realizado ao bombear um líquido de uma altura para outra.
- Encontre a força hidrostática contra uma placa vertical submersa.
Nesta seção, examinamos algumas aplicações físicas da integração. Vamos começar com uma análise do cálculo da massa a partir de uma função de densidade. Em seguida, voltamos nossa atenção para o trabalho e fechamos a seção com um estudo da força hidrostática.
Massa e densidade
Podemos usar a integração para desenvolver uma fórmula para calcular a massa com base em uma função de densidade. Primeiro, consideramos uma haste ou fio fino. Oriente a haste de forma que ela se alinhe com o\(x\) eixo -, com a extremidade esquerda da haste em\(x=a\) e a extremidade direita da haste em\(x=b\) (Figura\(\PageIndex{1}\)). Observe que, embora retratemos a haste com alguma espessura nas figuras, para fins matemáticos, assumimos que a haste é fina o suficiente para ser tratada como um objeto unidimensional.
Se a haste tiver densidade constante\(ρ\), dada em termos de massa por unidade de comprimento, então a massa da haste é apenas o produto da densidade e do comprimento da haste:\((b−a)ρ\). Se a densidade da haste não for constante, no entanto, o problema se torna um pouco mais desafiador. Quando a densidade da haste varia de ponto a ponto, usamos uma função de densidade linear,\(ρ(x)\), para denotar a densidade da haste em qualquer ponto,\(x\). \(ρ(x)\)Seja uma função de densidade linear integrável. Agora,\(i=0,1,2,…,n\)\(P={x_i}\) seja uma partição regular do intervalo\([a,b]\) e\(i=1,2,…,n\) escolha um ponto arbitrário\(x^∗_i∈[x_{i−1},x_i]\). A figura\(\PageIndex{2}\) mostra um segmento representativo da haste.
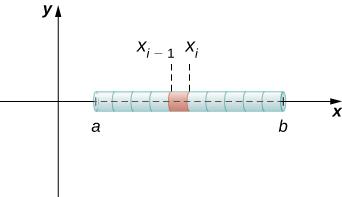
A massa\(m_i\) do segmento da haste de\(x_{i−1}\) para\(x_i\) é aproximada por
\[ \begin{align*} m_i ≈ρ(x^∗_i)(x_i−x_{i−1}) \\[4pt] =ρ(x^∗_i)Δx. \end{align*} \nonumber \]
A adição das massas de todos os segmentos nos dá uma aproximação da massa de toda a haste:
\[ \begin{align*} m =\sum_{i=1}^nm_i \\[4pt] ≈\sum_{i=1}^nρ(x^∗_i)Δx. \end{align*} \nonumber \]
Esta é uma soma de Riemann. Tomando o limite como\(n→∞\), obtemos uma expressão para a massa exata da haste:
\[ \begin{align*} m =\lim_{n→∞}\sum_{i=1}^nρ(x^∗_i)Δx \\[4pt] =\int ^b_aρ(x)dx. \end{align*} \nonumber \]
Declaramos esse resultado no seguinte teorema.
Dada uma haste fina orientada ao longo do\(x\) eixo -ao longo do intervalo\([a,b]\), vamos\(ρ(x)\) denotar uma função de densidade linear que fornece a densidade da haste\(x\) em um ponto no intervalo. Em seguida, a massa da haste é dada por
\[m=\int ^b_aρ(x)dx. \label{density1} \]
Nós aplicamos esse teorema no próximo exemplo.
Considere uma haste fina orientada no\(x\) eixo -ao longo do intervalo\([π/2,π]\). Se a densidade da haste for dada por\(ρ(x)=\sin x\), qual é a massa da haste?
Solução
Aplicando a Equação\ ref {density1} diretamente, temos
\[ \begin{align*} m =\int ^b_aρ(x)dx \nonumber \\[4pt] = \int ^π_{π/2}\sin x \,dx \nonumber \\[4pt] = −\cos x \Big|^π_{π/2} \nonumber \\[4pt] = 1. \nonumber \end{align*}\]
Considere uma haste fina orientada no\(x\) eixo -ao longo do intervalo\([1,3]\). Se a densidade da haste for dada por\(ρ(x)=2x^2+3,\) qual é a massa da haste?
- Dica
-
Use o processo do exemplo anterior.
- Solução
-
\(70/3\)
Agora estendemos esse conceito para encontrar a massa de um disco bidimensional de raio\(r\). Como na haste que analisamos no caso unidimensional, aqui assumimos que o disco é fino o suficiente para que, para fins matemáticos, possamos tratá-lo como um objeto bidimensional. Assumimos que a densidade é dada em termos de massa por unidade de área (chamada densidade de área) e, além disso, assumimos que a densidade varia apenas ao longo do raio do disco (chamada densidade radial). Orientamos o disco no\(xy-plane\), com o centro na origem. Então, a densidade do disco pode ser tratada como uma função de\(x\), denotada\(ρ(x)\). Presumimos que\(ρ(x)\) seja integrável. Como a densidade é uma função de\(x\), dividimos o intervalo\([0,r]\) ao longo do\(x\) eixo y. Para\(i=0,1,2,…,n\),\(P={x_i}\) seja uma partição regular do intervalo e\([0,r]\), para\(i=1,2,…,n\), escolha um ponto arbitrário\(x^∗_i∈[x_{i−1},x_i]\). Agora, use a partição para dividir o disco em arruelas finas (bidimensionais). Um disco e uma lavadora representativa são mostrados na figura a seguir.
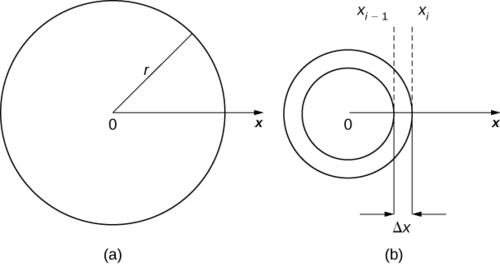
Agora, aproximamos a densidade e a área da lavadora para calcular uma massa aproximada,\(m_i\). Observe que a área da lavadora é dada por
\[ \begin{align*} A_i =π(x_i)^2−π(x_{i−1})^2 \\[4pt] =π[x^2_i−x^2_{i−1}] \\[4pt] =π(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =π(x_i+x_{i−1})Δx. \end{align*}\]
Você deve se lembrar de que tínhamos uma expressão semelhante a essa quando calculávamos volumes por conchas. Como fizemos lá, usamos\(x^∗_i≈(x_i+x_{i−1})/2\) para aproximar o raio médio da lavadora. Nós obtemos
\[A_i=π(x_i+x_{i−1})Δx≈2πx^∗_iΔx. \nonumber \]
Usando\(ρ(x^∗_i)\) para aproximar a densidade da lavadora, aproximamos a massa da lavadora em
\[m_i≈2πx^∗_iρ(x^∗_i)Δx. \nonumber \]
Somando as massas das arruelas, vemos que a massa\(m\) de todo o disco é aproximada por
\[m=\sum_{i=1}^nm_i≈\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx. \nonumber \]
Mais uma vez, reconhecemos isso como uma soma de Riemann e consideramos o limite que\(n→∞.\) Isso nos dá
\[ \begin{align*} m =\lim_{n→∞}\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx \\[4pt] =\int ^r_02πxρ(x)dx. \end{align*}\]
Resumimos essas descobertas no seguinte teorema.
\(ρ(x)\)Seja uma função integrável representando a densidade radial de um disco de raio\(r\). Em seguida, a massa do disco é dada por
\[m=\int ^r_02πxρ(x)dx. \label{massEq1} \]
Vamos\(ρ(x)=\sqrt{x}\) representar a densidade radial de um disco. Calcule a massa de um disco de raio 4.
Solução
Aplicando a Equação\ ref {masseQ1}, encontramos
\[ \begin{align*} m =\int ^r_02πxρ(x)dx \nonumber \\[4pt] =\int ^4_02πx\sqrt{x}dx=2π\int ^4_0x^{3/2}dx \nonumber \\[4pt] =2π\dfrac{2}{5}x^{5/2}∣^4_0=\dfrac{4π}{5}[32] \nonumber \\[4pt] =\dfrac{128π}{5}.\nonumber \end{align*}\]
Vamos\(ρ(x)=3x+2\) representar a densidade radial de um disco. Calcule a massa de um disco de raio 2.
- Dica
-
Use o processo do exemplo anterior.
- Solução
-
\(24π\)
Trabalho realizado por uma força
Agora consideramos o trabalho. Em física, o trabalho está relacionado à força, que geralmente é definida intuitivamente como empurrar ou puxar um objeto. Quando uma força move um objeto, dizemos que a força funciona no objeto. Em outras palavras, o trabalho pode ser considerado como a quantidade de energia necessária para mover um objeto. De acordo com a física, quando temos uma força constante, o trabalho pode ser expresso como o produto da força e da distância.
No sistema inglês, a unidade de força é a libra e a unidade de distância é o pé, então o trabalho é dado em libras-pé. No sistema métrico, quilogramas e metros são usados. Um newton é a força necessária para acelerar o\(1\) quilograma de massa à taxa de\(1\) m/seg 2. Assim, a unidade de trabalho mais comum é o medidor de newtons. Essa mesma unidade também é chamada de joule. Ambos são definidos como quilogramas vezes metros quadrados sobre segundos quadrados\((kg⋅m^2/s^2).\)
Quando temos uma força constante, as coisas são bem fáceis. É raro, no entanto, que uma força seja constante. O trabalho realizado para comprimir (ou alongar) uma mola, por exemplo, varia dependendo de até que ponto a mola já foi comprimida (ou esticada). Examinaremos as molas com mais detalhes posteriormente nesta seção.
Suponha que tenhamos uma força variável\(F(x)\) que move um objeto em uma direção positiva ao longo do\(x\) eixo -de um ponto\(a\) a outro\(b\). Para calcular o trabalho realizado, dividimos o intervalo\([a,b]\) e estimamos o trabalho realizado em cada subintervalo. Então, para\(i=0,1,2,…,n\),\(P={x_i}\) seja uma partição regular do intervalo e\([a,b]\), para\(i=1,2,…,n\), escolha um ponto arbitrário\(x^∗_i∈[x_{i−1},x_i]\). Para calcular o trabalho realizado para mover um objeto de um ponto\(x_{i−1}\) a ponto\(x_i\), assumimos que a força é aproximadamente constante ao longo do intervalo e usamos\(F(x^∗_i)\) para aproximar a força. O trabalho realizado ao longo do intervalo\([x_{i−1},x_i]\), então, é dado por
\[W_i≈F(x^∗_i)(x_{i}−x_{i−1})=F(x^∗_i)Δx. \nonumber \]
Portanto, o trabalho realizado ao longo do intervalo\([a,b]\) é de aproximadamente
\[W=\sum_{i=1}^nW_i≈\sum_{i=1}^nF(x^∗_i)Δx. \nonumber \]
Tomar o limite dessa expressão como nos\(n→∞\) dá o valor exato do trabalho:
\[ \begin{align*} W =\lim_{n→∞}\sum_{i=1}^nF(x^∗_i)Δx \\[4pt] =\int ^b_aF(x)dx. \end{align*}\]
Assim, podemos definir o trabalho da seguinte forma.
Se uma força variável\(F(x)\) move um objeto em uma direção positiva ao longo do\(x\) eixo -de um ponto\(a\) a\(b\) outro, então o trabalho realizado no objeto é
\[W=\int ^b_aF(x)dx. \label{work} \]
Observe que, se\(F\) for constante, a integral avalia\(F⋅(b−a)=F⋅d,\) qual é a fórmula que declaramos no início desta seção.
Agora, vejamos o exemplo específico do trabalho realizado para comprimir ou alongar uma mola. Considere um bloco preso a uma mola horizontal. O bloco se move para frente e para trás à medida que a mola se estica e se comprime. Embora no mundo real tivéssemos que considerar a força de atrito entre o bloco e a superfície na qual ele está apoiado, ignoramos o atrito aqui e assumimos que o bloco está apoiado em uma superfície sem atrito. Quando a mola está em seu comprimento natural (em repouso), diz-se que o sistema está em equilíbrio. Nesse estado, a mola não é alongada nem comprimida e, nessa posição de equilíbrio, o bloco não se move até que alguma força seja introduzida. Orientamos o sistema de forma que\(x=0\) corresponda à posição de equilíbrio (Figura\(\PageIndex{4}\)).
De acordo com a lei de Hooke, a força necessária para comprimir ou esticar uma mola a partir de uma posição de equilíbrio é dada por\(F(x)=kx\), para alguma constante\(k\). O valor de k depende das características físicas da mola. A constante\(k\) é chamada de constante de mola e é sempre positiva. Podemos usar essas informações para calcular o trabalho realizado para comprimir ou alongar uma mola, conforme mostrado no exemplo a seguir.
Suponha que seja necessária uma força de\(10\) N (na direção negativa) para comprimir uma mola\(0.2\) m da posição de equilíbrio. Quanto trabalho é feito para esticar a mola\(0.5\) m da posição de equilíbrio?
Solução
Primeiro encontre a constante da mola,\(k\). Quando\(x=−0.2\), nós sabemos que\(F(x)=−10,\) sim
\[ \begin{align*} F(x) =kx \\[4pt] −10 =k(−0.2) \\[4pt] k =50 \end{align*}\]
e\(F(x)=50x.\) então, para calcular o trabalho, integramos a função de força, obtendo
\[\begin{align*} W = \int ^b_aF(x)dx \\[4pt] =\int ^{0.5}_050 x \,dx \\[4pt] =\left. 25x^2 \right|^{0.5}_0 \\[4pt] =6.25. \end{align*}\]
O trabalho realizado para esticar a mola é\(6.25\) J.
Suponha que seja necessária uma força de\(8\) lb para esticar uma mola\(6\) pol. da posição de equilíbrio. Quanto trabalho é feito para esticar os\(1\) pés da mola da posição de equilíbrio?
- Dica
-
Use o processo do exemplo anterior. Tenha cuidado com as unidades.
- Solução
-
\(8\)ft-lb
Trabalho realizado no bombeamento
Considere o trabalho realizado para bombear água (ou algum outro líquido) de um tanque. Os problemas de bombeamento são um pouco mais complicados do que os problemas de mola, porque muitos dos cálculos dependem da forma e do tamanho do tanque. Além disso, em vez de nos preocuparmos com o trabalho realizado para mover uma única massa, estamos analisando o trabalho realizado para mover um volume de água, e é mais trabalhoso mover a água do fundo do tanque do que mover a água da parte superior do tanque.
Examinamos o processo no contexto de um tanque cilíndrico e, em seguida, examinamos alguns exemplos usando tanques de diferentes formas. Suponha que um tanque cilíndrico de raio\(4\)\(10\) m e altura m esteja cheio até uma profundidade de 8 m. Quanto trabalho é necessário para bombear toda a água pela borda superior do tanque?
A primeira coisa que precisamos fazer é definir um quadro de referência. Deixamos\(x\) representar a distância vertical abaixo da parte superior do tanque. Ou seja, orientamos o\(x\) eixo -verticalmente, com a origem na parte superior do tanque e a direção descendente sendo positiva (Figura\(\PageIndex{5}\)).
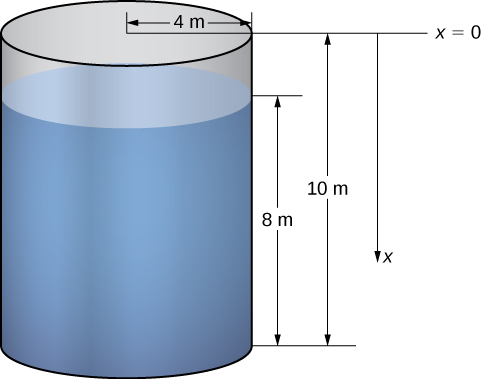
Usando esse sistema de coordenadas, a água se estende\(x=2\) de\(x=10\) a. Portanto, dividimos o intervalo\([2,10]\) e analisamos o trabalho necessário para levantar cada “camada” individual de água. Então, para\(i=0,1,2,…,n\),\(P={x_i}\) seja uma partição regular do intervalo e\([2,10]\), para\(i=1,2,…,n\), escolha um ponto arbitrário\(x^∗_i∈[x_{i−1},x_i]\). A figura\(\PageIndex{6}\) mostra uma camada representativa.
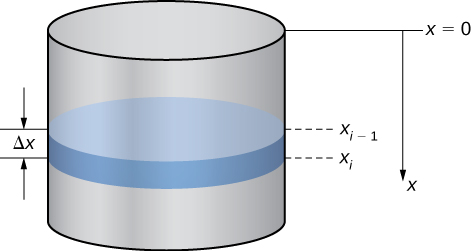
Em problemas de bombeamento, a força necessária para levantar a água até o topo do tanque é a força necessária para superar a gravidade, portanto, é igual ao peso da água. Dado que a densidade de peso da água é\(9800 \, \text{N/m}^3\), ou\(62.4\,\text{lb/ft}^3\), o cálculo do volume de cada camada nos dá o peso. Nesse caso, temos
\[V=π(4)^2Δx=16πΔx. \nonumber \]
Então, a força necessária para levantar cada camada é
\[F=9800⋅16πΔx=156,800πΔx. \nonumber \]
Observe que essa etapa se torna um pouco mais difícil se tivermos um tanque não cilíndrico. Examinaremos um tanque não cilíndrico no próximo exemplo.
Também precisamos saber a distância em que a água deve ser levantada. Com base em nossa escolha de sistemas de coordenadas, podemos usar\(x^∗_i\) como uma aproximação da distância que a camada deve ser levantada. Então, o trabalho para levantar a\(i^{\text{th}}\) camada de água\(W_i\) é de aproximadamente
\[W_i≈156,800πx^∗_iΔx. \nonumber \]
Adicionando o trabalho para cada camada, vemos que o trabalho aproximado para esvaziar o tanque é dado por
\[ \begin{align*} W =\sum_{i=1}^nW_i \\[4pt] ≈\sum_{i=1}^n156,800πx^∗_iΔx.\end{align*}\]
Esta é uma soma de Riemann, então, considerando o limite conforme\(n→∞,\) obtemos
\[ \begin{align*} W =\lim_{n→∞}\sum^n_{i=1}156,800πx^∗_iΔx \\[4pt] = 156,800π\int ^{10}_2xdx \\[4pt] =156,800π \left( \dfrac{x^2}{2}\right)\bigg|^{10}_2=7,526,400π≈23,644,883. \end{align*}\]
O trabalho necessário para esvaziar o tanque é de aproximadamente 23.650.000 J.
Para problemas de bombeamento, os cálculos variam de acordo com a forma do tanque ou recipiente. A estratégia de resolução de problemas a seguir apresenta um processo passo a passo para resolver problemas de bombeamento.
- Desenhe uma imagem do tanque e selecione um quadro de referência apropriado.
- Calcule o volume de uma camada representativa de água.
- Multiplique o volume pela densidade de peso da água para obter a força.
- Calcule a distância em que a camada de água deve ser levantada.
- Multiplique a força e a distância para obter uma estimativa do trabalho necessário para levantar a camada de água.
- Soma o trabalho necessário para levantar todas as camadas. Essa expressão é uma estimativa do trabalho necessário para bombear a quantidade desejada de água e está na forma de uma soma de Riemann.
- Considere o limite\(n→∞\) e avalie a integral resultante para obter o trabalho exato necessário para bombear a quantidade desejada de água.
Agora aplicamos essa estratégia de solução de problemas em um exemplo com um tanque não cilíndrico.
Suponha um tanque na forma de um cone invertido, com altura\(12\) ft e raio base\(4\) ft. O tanque está cheio para começar, e a água é bombeada pela borda superior do tanque até que a altura da água restante no tanque seja de\(4\) pés. Quanto trabalho é necessário para bombear essa quantidade de água?
Solução
O tanque está representado na Figura\(\PageIndex{7}\). Como fizemos no exemplo com o tanque cilíndrico, orientamos o\(x\) eixo -verticalmente, com a origem na parte superior do tanque e a direção descendente sendo positiva (etapa 1).
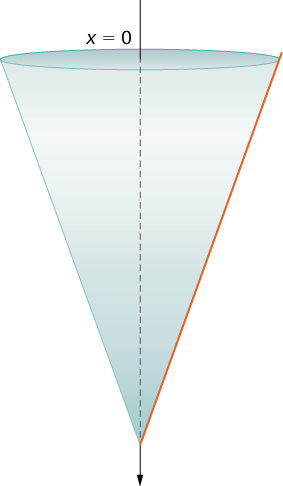
O tanque começa cheio e termina com\(4\) pés de água restantes, então, com base em nosso quadro de referência escolhido, precisamos dividir o intervalo\([0,8]\). Então, para\(i=0,1,2,…,n\),\(P={x_i}\) seja uma partição regular do intervalo e\([0,8]\), para\(i=1,2,…,n\), escolha um ponto arbitrário\(x^∗_i∈[x_{i−1},x_i]\). Podemos aproximar o volume de uma camada usando um disco e, em seguida, usar triângulos semelhantes para encontrar o raio do disco (Figura\(\PageIndex{8}\)).
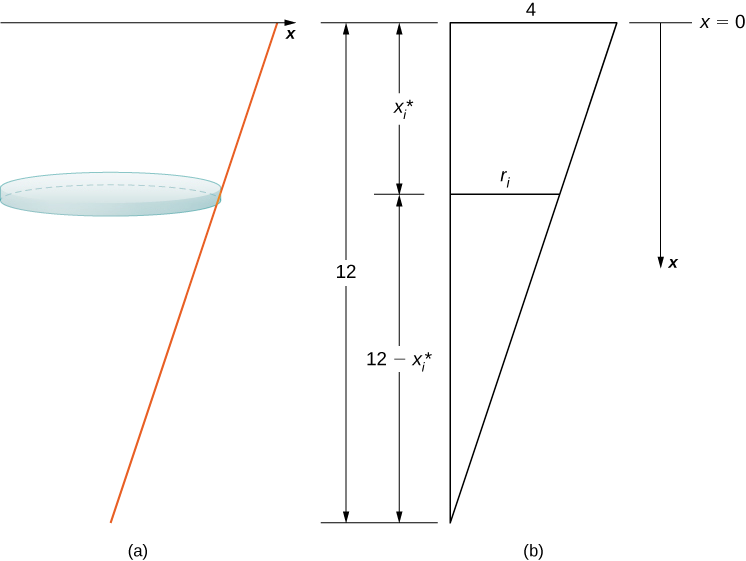
A partir de propriedades de triângulos semelhantes, temos
\[ \begin{align*} \dfrac{r_i}{12−x^∗_i} =\dfrac{4}{12} \tag{step 1} =\dfrac{1}{3} \\[4pt] 3r_i =12−x^∗_i \\[4pt] r_i =\dfrac{12−x^∗_i}{3} \\[4pt] =4−\dfrac{x^∗_i}{3}. \end{align*} \]
Em seguida, o volume do disco é
\[V_i=π \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 2} \]
A densidade de peso da água é\(62.4\) lb/ft 3, então a força necessária para levantar cada camada é de aproximadamente
\[F_i≈62.4π\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx \tag{step 3} \]
Com base no diagrama, a distância em que a água deve ser levantada é de aproximadamente\(x^∗_i\) pés (etapa 4), portanto, o trabalho aproximado necessário para levantar a camada é
\[W_i≈62.4πx^∗_i\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 5} \]
Somando o trabalho necessário para levantar todas as camadas, obtemos um valor aproximado do trabalho total:
\[W=\sum_{i=1}^nW_i≈\sum_{i=1}^n62.4πx^∗_i \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 6} \]
Tomando o limite à medida\(n→∞,\) que obtemos
\[ \begin{align*} W =\lim_{n→∞}\sum^n_{i=1}62.4πx^∗_i(4−\dfrac{x^∗_i}{3})^2Δx \\[4pt] = \int ^8_062.4πx \left(4−\dfrac{x}{3}\right)^2dx \\[4pt] = 62.4π\int ^8_0x \left(16−\dfrac{8x}{3}+\dfrac{x^2}{9}\right)\,dx=62.4π\int ^8_0 \left(16x−\dfrac{8x^2}{3}+\dfrac{x^3}{9}\right)\,dx \\[4pt] =62.4π\left[8x^2−\dfrac{8x^3}{9}+\dfrac{x^4}{36}\right]\bigg|^8_0=10,649.6π≈33,456.7. \end{align*}\]
É preciso aproximadamente um quilo\(33,450\) de trabalho para esvaziar o tanque até o nível desejado.
Um tanque tem a forma de um cone invertido, com altura\(10\) pés e raio base 6 pés. O tanque é enchido até uma profundidade de 8 pés para começar, e a água é bombeada pela borda superior do tanque até que 3 pés de água permaneçam no tanque. Quanto trabalho é necessário para bombear essa quantidade de água?
- Dica
-
Use o processo do exemplo anterior.
- Solução
-
Aproximadamente\(43,255.2\) pés-lb
Força e pressão hidrostáticas
Nesta última seção, examinamos a força e a pressão exercidas sobre um objeto submerso em um líquido. No sistema inglês, a força é medida em libras. No sistema métrico, ele é medido em newtons. Pressão é força por unidade de área, então, no sistema inglês, temos libras por pé quadrado (ou, talvez mais comumente, libras por polegada quadrada, denotado psi). No sistema métrico, temos newtons por metro quadrado, também chamados de pascais.
Vamos começar com o caso simples de uma placa de área\(A\) submersa horizontalmente em água a uma profundidade s (Figura\(\PageIndex{9}\)). Então, a força exercida na placa é simplesmente o peso da água acima dela, que é dado por\(F=ρAs\), onde\(ρ\) está a densidade de peso da água (peso por unidade de volume). Para encontrar a pressão hidrostática, ou seja, a pressão exercida pela água sobre um objeto submerso, dividimos a força pela área. Então, a pressão é\(p=F/A=ρs\).
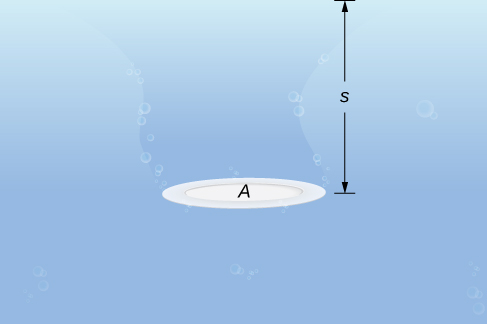
Pelo princípio de Pascal, a pressão em uma determinada profundidade é a mesma em todas as direções, portanto, não importa se a placa está submersa na horizontal ou na vertical. Então, desde que saibamos a profundidade, conhecemos a pressão. Podemos aplicar o princípio de Pascal para encontrar a força exercida em superfícies, como barragens, orientadas verticalmente. Não podemos aplicar a fórmula\(F=ρAs\) diretamente, porque a profundidade varia de ponto a ponto em uma superfície orientada verticalmente. Então, como fizemos muitas vezes antes, formamos uma partição, uma soma de Riemann e, finalmente, uma integral definida para calcular a força.
Suponha que uma placa fina esteja submersa na água. Escolhemos nosso quadro de referência de forma que o\(x\) eixo -seja orientado verticalmente, com a direção descendente sendo positiva e o ponto\(x=0\) correspondente a um ponto de referência lógico. Vamos\(s(x)\) indicar a profundidade no ponto x. Observe que muitas vezes deixamos\(x=0\) corresponder à superfície da água. Nesse caso, a profundidade em qualquer ponto é simplesmente dada por\(s(x)=x\). No entanto, em alguns casos, podemos querer selecionar um ponto de referência diferente para\(x=0\), portanto, prosseguimos com o desenvolvimento no caso mais geral. Por último, deixe\(w(x)\) indicar a largura da placa no ponto\(x\).
Suponha que a borda superior da placa esteja no ponto\(x=a\) e a borda inferior da placa esteja no ponto\(x=b\). Então, para\(i=0,1,2,…,n\),\(P={x_i}\) seja uma partição regular do intervalo e\([a,b]\), para\(i=1,2,…,n\), escolha um ponto arbitrário\(x^∗_i∈[x_{i−1},x_i]\). A divisória divide a placa em várias tiras finas e retangulares (Figura\(\PageIndex{10}\)).
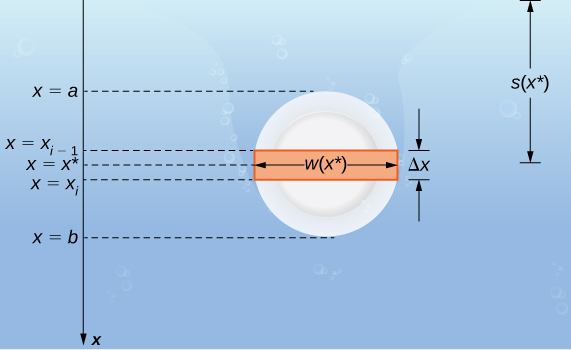
Vamos agora estimar a força em uma faixa representativa. Se a faixa for fina o suficiente, podemos tratá-la como se estivesse em uma profundidade constante\(s(x^∗_i)\). Em seguida, temos
\[F_i=ρAs=ρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber \]
Somando as forças, obtemos uma estimativa da força na placa:
\[F≈\sum_{i=1}^nF_i=\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber \]
Esta é uma soma de Riemann, então, tomar o limite nos dá a força exata. Nós obtemos
\[F=\lim_{n→∞}\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i)=\int ^b_aρw(x)s(x)dx. \label{eqHydrostatic} \]
Avaliar essa integral nos dá a força na placa. Resumimos isso na seguinte estratégia de solução de problemas.
- Desenhe uma imagem e selecione um quadro de referência apropriado. (Observe que, se selecionarmos um quadro de referência diferente do usado anteriormente, talvez precisemos ajustar a Equação\ ref {eqHydrostatic} de acordo.)
- Determine as funções de profundidade e largura\(s(x)\) e\(w(x).\)
- Determine a densidade de peso de qualquer líquido com o qual você está trabalhando. A densidade de peso da água é\(62.4 \,\text{lb/ft}^3\), ou\(9800 \,\text{N/m}^3\).
- Use a equação para calcular a força total.
Um bebedouro de 15 pés de comprimento tem extremidades em forma de triângulos isósceles invertidos, com base de 8 pés e altura de 3 pés. Encontre a força em uma extremidade da calha se a calha estiver cheia de água.
Solução
A figura\(\PageIndex{11}\) mostra a calha e uma visão mais detalhada de uma extremidade.
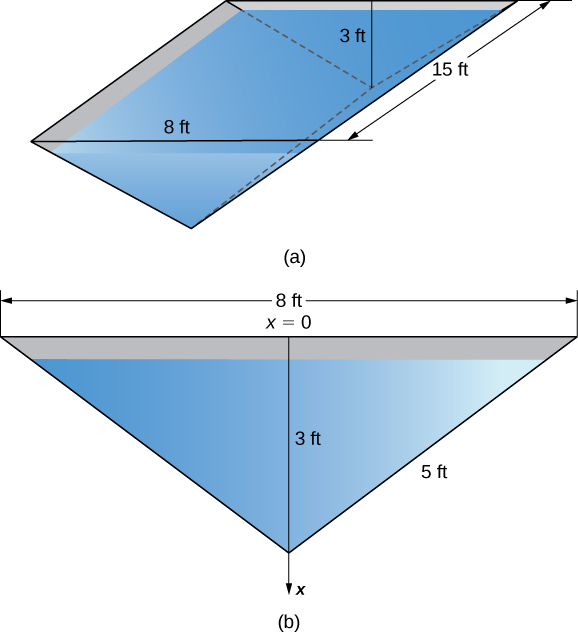
Selecione um quadro de referência com o\(x\) eixo -orientado verticalmente e a direção descendente sendo positiva. Selecione a parte superior da calha como o ponto correspondente a\(x=0\) (etapa 1). A função de profundidade, então, é\(s(x)=x\). Usando triângulos semelhantes, vemos isso\(w(x)=8−(8/3)x\) (etapa 2). Agora, a densidade de peso da água é\(62.4 \,\text{lb/ft}^3\) (etapa 3), então aplicando a Equação\ ref {eqHydrostatic}, obtemos
\[ \begin{align*} F =\int ^b_aρw(x)s(x)dx \\[4pt] = \int ^3_062.4 \left(8−\dfrac{8}{3}x\right) x \,dx=62.4\int ^3_0 \left(8x−\dfrac{8}{3}x^2 \right)dx \\[4pt] = \left.62.4 \left[4x^2−\dfrac{8}{9}x^3\right]\right|^3_0=748.8. \end{align*}\]
A água exerce uma força de 748,8 lb na extremidade da calha (etapa 4).
Um bebedouro de 12 m de comprimento tem pontas em forma de triângulos isósceles invertidos, com base de 6 m e altura de 4 m. Encontre a força em uma extremidade da calha se a calha estiver cheia de água.
- Dica
-
Siga a estratégia de resolução de problemas e o processo do exemplo anterior.
- Solução
-
\(156,800\)N
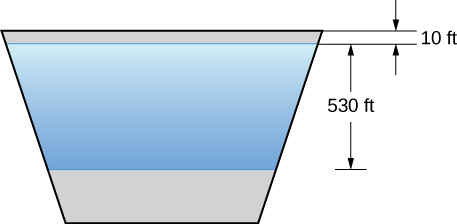
Agora voltamos nossa atenção para a Represa Hoover, mencionada no início deste capítulo. A barragem real é arqueada, em vez de plana, mas faremos algumas suposições simplificadoras para nos ajudar com os cálculos. Suponha que a face da Barragem Hoover tenha a forma de um trapézio isósceles com base inferior de 750 pés, base superior de 1250 pés e altura de 750 pés (veja a figura a seguir).

Quando o reservatório está cheio, a profundidade máxima do Lago Mead é de cerca de 530 pés e a superfície do lago está cerca de 10 pés abaixo do topo da barragem (veja a figura a seguir).
- Encontre a força na face da represa quando o reservatório estiver cheio.
- O sudoeste dos Estados Unidos está passando por uma seca, e a superfície do Lago Mead está cerca de 125 pés abaixo de onde estaria se o reservatório estivesse cheio. Qual é a força na face da barragem nessas circunstâncias?
Solução:
uma.
Começamos estabelecendo um quadro de referência. Como de costume, optamos por orientar o\(x\) eixo -verticalmente, com a direção descendente sendo positiva. Desta vez, no entanto, vamos deixar\(x=0\) representar o topo da barragem, em vez da superfície da água. Quando o reservatório está cheio, a superfície da água está\(10\) pés abaixo do topo da barragem, portanto\(s(x)=x−10\) (veja a figura a seguir).

Para encontrar a função de largura, voltamos novamente para triângulos semelhantes, conforme mostrado na figura abaixo.
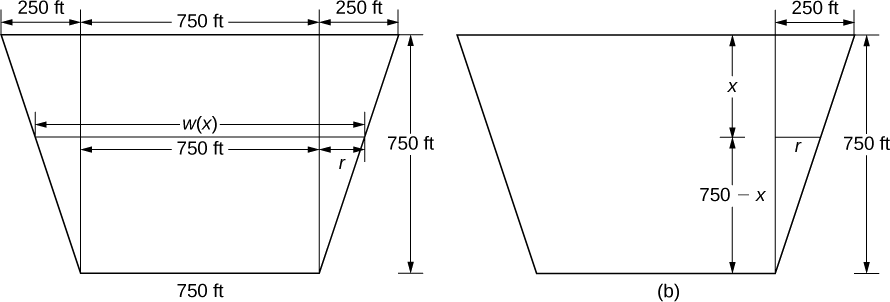
A partir da figura, vemos isso\(w(x)=750+2r\). Usando propriedades de triângulos semelhantes, obtemos\(r=250−(1/3)x\). Assim,
\[w(x)=1250−\dfrac{2}{3}x \tag{step 2} \]
Usando uma densidade de peso de\(62.4\) lb/ft 3 (etapa 3) e aplicando a Equação\ ref {eqHydrostatic}, obtemos
\ [\ begin {align*} F =\ int^b_a ρ w (x) s (x)\, dx\\ [4pt]
=\ int ^ {540} _ {10} 62,4\ esquerda (1250−\ dfrac {2} {3} x\ direita) (x−10)\, dx\\ [4pt]
=62,4\ int ^ {540} {10} −\ dfrac {2} {3} [x^2−1885x+18750]\, dx\\ [4pt]
=−62,4\ esquerda (\ dfrac {2} {3}\ direita)\ esquerda [\ dfrac {x^3} {3} −\ dfrac {1885x^2} {2} +18750x\ certo]\ bigg|^ {540} _ {10} ≈ 8.832.245.000\,\ text {lb} =4.416,122,5\,\ text {t}. \ end {align*}\]
Observe a mudança de libras para toneladas (\(2000\)lb =\(1\) tonelada) (etapa 4). Isso muda nossa função de\(s(x)\) profundidade e nossos limites de integração. Nós temos\(s(x)=x−135\). O limite inferior de integração é 135. O limite superior permanece\(540\). Avaliando a integral, obtemos
\ [\ begin {align*} F =\ int^b_aρ w (x) s (x)\, dx\\ [4pt]
=\ int ^ {540} _ {135} 62,4\ esquerda (1250−\ dfrac {2} {3} x\ direita) (x−135)\, dx\\ [4pt]
=−62,4 (\ dfrac {2} {3})\ int ^ {540} _ {135} (x−1875) (x−135)\, dx=−62,4\ left (\ dfrac {2} {3}\ direita)\ int ^ {540} _ {135} (x^2−2010x+253125)\, dx\\ [4pt]
=−62,4\ left (\ dfrac {2} {3}\ right)\ left [\ dfrac {x^3} {3} −1005x^2+253125x\ right]\ bigg|^ {540} _ {135} ≈ 5.015.230.000\,\ text {lb} =2.507.615\,\ texto {t}. \ end {align*}\]
Quando o reservatório está em seu nível médio, a superfície da água fica cerca de 50 pés abaixo de onde estaria se o reservatório estivesse cheio. Qual é a força na face da barragem nessas circunstâncias?
- Dica
-
Altere a função de profundidade\(s(x),\) e os limites da integração.
- Solução
-
Aproximadamente 7.164.520.000 libras ou 3.582.260 t
Conceitos-chave
- Várias aplicações físicas da integral definida são comuns em engenharia e física.
- Integrais definidas podem ser usadas para determinar a massa de um objeto se sua função de densidade for conhecida.
- O trabalho também pode ser calculado a partir da integração de uma função de força ou ao neutralizar a força da gravidade, como em um problema de bombeamento.
- Integrais definidas também podem ser usadas para calcular a força exercida sobre um objeto submerso em um líquido.
Equações-chave
- Massa de um objeto unidimensional
\( \displaystyle m=\int ^b_aρ(x)dx\)
- Massa de um objeto circular
\(\displaystyle m=\int ^r_02πxρ(x)dx\)
- Trabalho realizado em um objeto
\(\displaystyle W=\int ^b_aF(x)dx\)
- Força hidrostática em uma placa
\(\displaystyle F=\int ^b_aρw(x)s(x)dx\)
Glossário
- função de densidade
- uma função de densidade descreve como a massa é distribuída por um objeto; pode ser uma densidade linear, expressa em termos de massa por unidade de comprimento; uma densidade de área, expressa em termos de massa por unidade de área; ou uma densidade de volume, expressa em termos de massa por unidade de volume; a densidade de peso também é usada para descrever peso (em vez de massa) por unidade de volume
- Lei de Hooke
- esta lei estabelece que a força necessária para comprimir (ou alongar) uma mola é proporcional à distância em que a mola foi comprimida (ou esticada) do equilíbrio; em outras palavras,\(F=kx\), onde\(k\) está uma constante
- pressão hidrostática
- a pressão exercida pela água sobre um objeto submerso
- trabalhar
- a quantidade de energia necessária para mover um objeto; na física, quando uma força é constante, o trabalho é expresso como o produto da força e da distância


