4.7: Problemas de otimização aplicados

Last updated
Save as PDF

Page ID: 188224

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Configure e resolva problemas de otimização em vários campos aplicados.

Uma aplicação comum do cálculo é calcular o valor mínimo ou máximo de uma função. Por exemplo, as empresas geralmente querem minimizar os custos de produção ou maximizar a receita. Na fabricação, muitas vezes é desejável minimizar a quantidade de material usado para embalar um produto com um determinado volume. Nesta seção, mostramos como configurar esses tipos de problemas de minimização e maximização e resolvê-los usando as ferramentas desenvolvidas neste capítulo.

Resolvendo problemas de otimização em um intervalo fechado e limitado

A ideia básica dos problemas de otimização que se seguem é a mesma. Temos uma quantidade específica que estamos interessados em maximizar ou minimizar. No entanto, também temos algumas condições auxiliares que precisam ser satisfeitas. Por exemplo, em$\PageIndex{1}$ Example, estamos interessados em maximizar a área de um jardim retangular. Certamente, se continuarmos aumentando os comprimentos laterais do jardim, a área continuará a ficar maior. No entanto, e se tivermos alguma restrição sobre a quantidade de cercas que podemos usar para o perímetro? Nesse caso, não podemos tornar o jardim tão grande quanto quisermos. Vamos ver como podemos maximizar a área de um retângulo sujeita a alguma restrição no perímetro.

Exemplo$\PageIndex{1}$: Maximizing the Area of a Garden

Um jardim retangular deve ser construído usando uma parede de pedra como um lado do jardim e uma cerca de arame para os outros três lados (Figura$\PageIndex{1}$). Dada a cerca$100\,\text{ft}$ de arame, determine as dimensões que criariam um jardim de área máxima. Qual é a área máxima?

O desenho de um jardim tem x e y escritos nos lados vertical e horizontal, respectivamente. Há uma parede de pedra percorrendo todo o comprimento horizontal inferior do desenho. — Figura$\PageIndex{1}$: Queremos determinar as medidas$x$ e$y$ isso criará um jardim com uma área máxima usando$100\,\text{ft}$ cercas.

Solução

Vamos$x$ indicar o comprimento da lateral do jardim perpendicular à parede de rocha e$y$ indicar o comprimento do lado paralelo à parede de rocha. Então a área do jardim é

$A=x⋅y.$

Queremos encontrar a área máxima possível, sujeita à restrição total da cerca$100\,\text{ft}$. A partir da Figura$\PageIndex{1}$, a quantidade total de cercas usadas será$2x+y.$ Portanto, a equação de restrição é

$2x+y=100.$

Resolvendo essa equação para$y$, temos$y=100−2x.$ Assim, podemos escrever a área como

$A(x)=x⋅(100−2x)=100x−2x^2.$

Antes de tentar maximizar a função de área,$A(x)=100x−2x^2,$ precisamos determinar o domínio em questão. Para construir um jardim retangular, certamente precisamos que os comprimentos dos dois lados sejam positivos. Portanto, precisamos$x>0$$y>0$ e. Desde$y=100−2x$, se$y>0$, então$x<50$. Portanto, estamos tentando determinar o valor máximo de$A(x)$ for$x$ durante o intervalo aberto$(0,50)$. Não sabemos se uma função necessariamente tem um valor máximo em um intervalo aberto. No entanto, sabemos que uma função contínua tem um máximo absoluto (e um mínimo absoluto) em um intervalo fechado. Portanto, vamos considerar a função no$A(x)=100x−2x^2$ intervalo fechado$[0,50]$. Se o valor máximo ocorrer em um ponto interno, encontramos o valor$x$ no intervalo aberto$(0,50)$ que maximiza a área do jardim.

Portanto, consideramos o seguinte problema:

Maximize$A(x)=100x−2x^2$ ao longo do intervalo$[0,50].$

Como mencionado anteriormente, como$A$ é uma função contínua em um intervalo fechado e limitado, pelo teorema do valor extremo, ela tem um máximo e um mínimo. Esses valores extremos ocorrem nos pontos finais ou nos pontos críticos. Nos pontos finais,$A(x)=0$. Como a área é positiva para todos$x$ no intervalo aberto$(0,50)$, o máximo deve ocorrer em um ponto crítico. Diferenciando a função$A(x)$, obtemos

$A′(x)=100−4x.$

Portanto, o único ponto crítico é$x=25$ (Figura$\PageIndex{2}$). Concluímos que a área máxima deve ocorrer quando$x=25$.

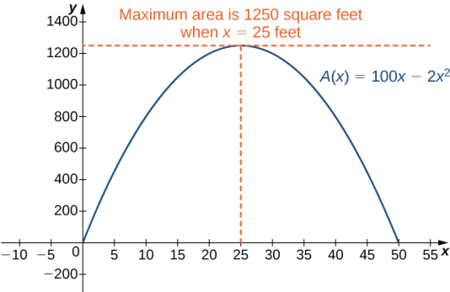
A função A (x) = 100x — 2x é representada graficamente. No máximo, há uma interseção de duas linhas tracejadas e um texto que diz “A área máxima é de 1250 pés quadrados quando x = 25 pés”. — Figura$\PageIndex{2}$: Para maximizar a área do jardim, precisamos encontrar o valor máximo da função$A(x)=100x−2x^2$.

Então temos que$y=100−2x=100−2(25)=50.$ maximizar a área do jardim, deixe$x=25\,\text{ft}$$y=50\,\text{ft}$ e. A área deste jardim é$1250\, \text{ft}^2$.

Exercício$\PageIndex{1}$

Determine a área máxima se quisermos fazer o mesmo jardim retangular da Figura$\PageIndex{2}$, mas temos$200\,\text{ft}$ de cercas.

Dica: Precisamos maximizar a função ao$A(x)=200x−2x^2$ longo do intervalo$[0,100].$

Responda: A área máxima é$5000\, \text{ft}^2$.

Agora, vamos ver uma estratégia geral para resolver problemas de otimização semelhante ao Example$\PageIndex{1}$.

Estratégia de resolução de problemas: resolvendo problemas de otimização

Introduza todas as variáveis. Se aplicável, desenhe uma figura e rotule todas as variáveis.
Determine qual quantidade deve ser maximizada ou minimizada e para qual faixa de valores das outras variáveis (se isso puder ser determinado neste momento).
Escreva uma fórmula para que a quantidade seja maximizada ou minimizada em termos das variáveis. Essa fórmula pode envolver mais de uma variável.
Escreva quaisquer equações relacionadas às variáveis independentes na fórmula da etapa$3$. Use essas equações para escrever a quantidade a ser maximizada ou minimizada em função de uma variável.
Identifique o domínio de consideração da função em etapa$4$ com base no problema físico a ser resolvido.
Localize o valor máximo ou mínimo da função a partir da etapa$4.$ Essa etapa normalmente envolve a busca de pontos críticos e a avaliação de uma função nos pontos finais.

Agora, vamos aplicar essa estratégia para maximizar o volume de uma caixa aberta, dada a restrição na quantidade de material a ser usado.

Exemplo$\PageIndex{2}$: Maximizing the Volume of a Box

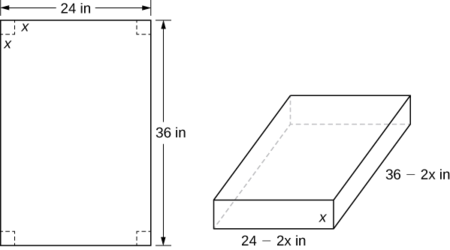
Uma caixa aberta deve ser feita de um$24\,\text{in.}$$36\,\text{in.}$ pedaço de papelão, removendo um quadrado de cada canto da caixa e dobrando as abas de cada lado. Qual tamanho quadrado deve ser cortado em cada canto para obter uma caixa com o volume máximo?

Solução

Etapa 1:$x$ Seja o comprimento lateral do quadrado a ser removido de cada canto (Figura$\PageIndex{3}$). Em seguida, as quatro abas restantes podem ser dobradas para formar uma caixa aberta. $V$Seja o volume da caixa resultante.

Existem dois números para essa figura. O primeiro é um retângulo com lados de 24 polegadas e 36 polegadas, com cada canto tendo um quadrado de comprimento lateral x retirado dele. Na segunda foto, há uma caixa com comprimentos laterais x pol, 24 - 2x in e 36 - 2x in. — Figura$\PageIndex{3}$: Um quadrado com$x$ polegadas de comprimento lateral é removido de cada canto do pedaço de papelão. As abas restantes são dobradas para formar uma caixa aberta.

Etapa 2: Estamos tentando maximizar o volume de uma caixa. Portanto, o problema é maximizar$V$.

Etapa 3: Conforme mencionado na etapa 2, estão tentando maximizar o volume de uma caixa. O volume de uma caixa é

\[V=L⋅W⋅H \nonumber, \nonumber \]

onde$L,\,W,$ e$H$ são o comprimento, a largura e a altura, respectivamente.

Etapa 4: Na Figura$\PageIndex{3}$, vemos que a altura da caixa é$x$ polegadas, o comprimento é$36−2x$ polegadas e a largura é$24−2x$ polegadas. Portanto, o volume da caixa é

\[ \begin{align*} V(x) &=(36−2x)(24−2x)x \\[4pt] &=4x^3−120x^2+864x \end{align*}. \nonumber \]

Etapa 5: Para determinar o domínio de consideração, vamos examinar a Figura$\PageIndex{3}$. Certamente, precisamos$x>0.$ Além disso, o comprimento lateral do quadrado não pode ser maior ou igual à metade do comprimento do lado mais curto$24\,\text{in.}$; caso contrário, uma das abas seria completamente cortada. Portanto, estamos tentando determinar se há um volume máximo da caixa$x$ acima do intervalo aberto.$(0,12).$ Como$V$ é uma função contínua no intervalo fechado$[0,12]$, sabemos que$V$ terá um máximo absoluto sobre o intervalo fechado. Portanto, consideramos o$V$ intervalo fechado$[0,12]$ e verificamos se o máximo absoluto ocorre em um ponto interno.

Etapa 6: Como$V(x)$ é uma função contínua sobre o intervalo fechado e limitado$[0,12]$,$V$ deve ter um máximo absoluto (e um mínimo absoluto). Uma$V(x)=0$ vez que nos pontos finais e$V(x)>0$$0<x<12,$ no máximo deve ocorrer em um ponto crítico. A derivada é

$V′(x)=12x^2−240x+864.$

Para encontrar os pontos críticos, precisamos resolver a equação

$12x^2−240x+864=0.$

Dividindo os dois lados dessa equação por$12$, o problema simplifica a solução da equação

$x^2−20x+72=0.$

Usando a fórmula quadrática, descobrimos que os pontos críticos são

\[\begin{align*} x &=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2} \\[4pt] &=\dfrac{20±\sqrt{112}}{2} \\[4pt] &=\dfrac{20±4\sqrt{7}}{2} \\[4pt] &=10±2\sqrt{7} \end{align*}. \nonumber \]

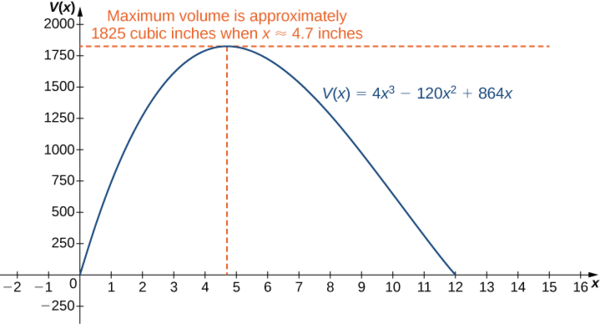
Como não$10+2\sqrt{7}$ está no domínio da consideração, o único ponto crítico que precisamos considerar é$10−2\sqrt{7}$. Portanto, o volume é maximizado se deixarmos$x=10−2\sqrt{7}\,\text{in.}$ O volume máximo é

\[V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\,\text{in}^3. \nonumber \]

conforme mostrado no gráfico a seguir.

A função V (x) = 4x3 — 120x2 + 864x é representada graficamente. No máximo, há uma interseção de duas linhas tracejadas e um texto que diz “O volume máximo é de aproximadamente 1825 polegadas cúbicas quando x ≈ 4,7 polegadas”. — Figura$\PageIndex{4}$: Maximizar o volume da caixa leva a encontrar o valor máximo de um polinômio cúbico.

Exercício$\PageIndex{2}$

Suponha que as dimensões do papelão no Exemplo$\PageIndex{2}$ sejam$20\,\text{in.}$ em$30\,\text{in.}$ Deixe$x$ ser o comprimento lateral de cada quadrado e escreva o volume da caixa aberta em função de$x$. Determine o domínio de consideração por$x$.

Dica: O volume da caixa é$L⋅W⋅H.$

Responda: $V(x)=x(20−2x)(30−2x).$O domínio é$[0,10]$.

Exemplo$\PageIndex{3}$: Minimizing Travel Time

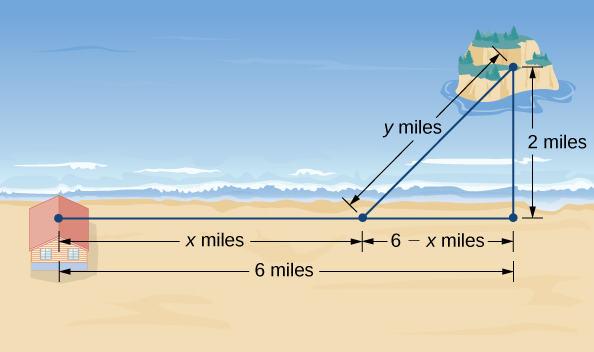
Uma ilha fica$2$ a milhas ao norte de seu ponto mais próximo ao longo de uma costa reta. Um visitante está hospedado em uma cabana na costa que$6$ fica a oeste desse ponto. O visitante está planejando ir da cabana para a ilha. Suponha que o visitante corra a uma taxa de$8$ mph e nade a uma taxa de$3$ mph. Até onde o visitante deve correr antes de nadar para minimizar o tempo necessário para chegar à ilha?

Solução

Etapa 1:$x$ Seja a distância percorrida e$y$ seja a distância de natação (Figura$\PageIndex{5}$). $T$Seja o tempo necessário para ir da cabana até a ilha.

A cabine fica a x milhas da costa. A partir desse ponto na costa, a ilha fica a milhas de distância. Se você continuasse a linha da cabine até a costa (a linha de x milhas) e se desenhasse uma linha da ilha paralela à costa, as linhas se estenderiam a 2 milhas da ilha e 6 milhas da cabine antes de se cruzarem. — Figura$\PageIndex{5}$: Como podemos escolher$x$ e$y$ minimizar o tempo de viagem da cabine até a ilha?

Etapa 2: O problema é minimizar$T$.

Etapa 3: Para descobrir o tempo gasto viajando da cabine para a ilha, adicione o tempo gasto correndo e o tempo gasto nadando. Como Distância = Taxa × Tempo,$(D=R×T),$ o tempo gasto correndo é

$T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}$,

e o tempo gasto nadando é

$T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}$.

Portanto, o tempo total gasto viajando é

$T=\dfrac{x}{8}+\dfrac{y}{3}$.

Etapa 4: Da Figura$\PageIndex{5}$, o segmento de linha de$y$ milhas forma a hipotenusa de um triângulo reto com pernas de comprimento$2$ mi e$6−x$ mi. Portanto, pelo teorema de Pitágoras,$2^2+(6−x)^2=y^2$, e obtemos$y=\sqrt{(6−x)^2+4}$. Assim, o tempo total gasto viajando é dado pela função

$T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}$.

Etapa 5: Na Figura$\PageIndex{5}$, vemos isso$0≤x≤6$. Portanto,$[0,6]$ é o domínio de consideração.

Etapa 6: Como$T(x)$ é uma função contínua em um intervalo fechado e limitado, ela tem um máximo e um mínimo. Vamos começar procurando por quaisquer pontos críticos$T$ acima do intervalo.$[0,6].$ A derivada é

\[\begin{align*} T′(x) &=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) \\[4pt] &=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}} \end{align*}\]

Se$T′(x)=0,$, então

\[\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}} \label{ex3eq1} \]

Portanto,

\[3\sqrt{(6−x)^2+4}=8(6−x). \label{ex3eq2} \]

Ao quadrado dos dois lados dessa equação, vemos que se$x$ satisfaz essa equação, então$x$ deve satisfazer

\[9[(6−x)^2+4]=64(6−x)^2,\nonumber \]

o que implica

\[55(6−x)^2=36. \nonumber \]

Concluímos que se$x$ é um ponto crítico, então$x$ satisfaz

\[(x−6)^2=\dfrac{36}{55}. \nonumber \]

[Observe que, como estamos fazendo o quadrado,$ (x-6)^2 = (6-x)^2.$]

Portanto, as possibilidades de pontos críticos são

\[x=6±\dfrac{6}{\sqrt{55}}.\nonumber \]

Como não$x=6+6/\sqrt{55}$ está no domínio, não é uma possibilidade para um ponto crítico. Por outro lado,$x=6−6/\sqrt{55}$ está no domínio. Como colocamos ao quadrado os dois lados da Equação\ ref {ex3eq2} para chegar aos possíveis pontos críticos, resta verificar se$x=6−6/\sqrt{55}$ satisfaz a Equação\ ref {ex3eq1}. Como$x=6−6/\sqrt{55}$ satisfaz essa equação, concluímos que$x=6−6/\sqrt{55}$ é um ponto crítico e é o único. Para justificar que o tempo é minimizado para esse valor de$x$, basta verificar os valores de$T(x)$ nos pontos finais$x=0$ e$x=6$ compará-los com o valor de$T(x)$ no ponto crítico$x=6−6/\sqrt{55}$. Descobrimos isso$T(0)≈2.108\,\text{h}$ e$T(6)≈1.417\,\text{h}$, enquanto

\[T(6−6/\sqrt{55})≈1.368\,\text{h}. \nonumber \]

Portanto, concluímos que$T$ tem um mínimo local em$x≈5.19$ mi.

Exercício$\PageIndex{3}$

Suponha que a ilha esteja a$1$ quilômetros da costa e a distância da cabine até o ponto na costa mais próximo da ilha seja$15$ mi. Suponha que um visitante nade a uma taxa de$2.5$ mph e corra a uma taxa de$6$ mph. Vamos$x$ indicar a distância que o visitante percorrerá antes de nadar e encontre uma função para o tempo que o visitante leva para ir da cabine até a ilha.

Dica: A hora$T=T_{running}+T_{swimming}.$

Responda: $T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5} $

Nos negócios, as empresas estão interessadas em maximizar a receita. No exemplo a seguir, consideramos um cenário em que uma empresa coletou dados sobre quantos carros é capaz de alugar, dependendo do preço que cobra de seus clientes pelo aluguel de um carro. Vamos usar esses dados para determinar o preço que a empresa deve cobrar para maximizar a quantidade de dinheiro que ela gera.

Exemplo$\PageIndex{4}$: Maximizing Revenue

Os proprietários de uma locadora de veículos determinaram que, se cobram dos clientes$p$ dólares por dia para alugar um carro$50≤p≤200$, onde o número de carros$n$ que alugam por dia pode ser modelado pela função linear$n(p)=1000−5p$. Se eles cobram$$50$ por dia ou menos, eles alugarão todos os seus carros. Se cobrarem$$200$ por dia ou mais, não alugarão nenhum carro. Supondo que os proprietários planejem cobrar dos clientes entre um$$50$$$200$ dia e um dia para alugar um carro, quanto eles devem cobrar para maximizar sua receita?

Solução

Etapa 1:$p$ Seja o preço cobrado por carro por dia e$n$ seja o número de carros alugados por dia. $R$Seja a receita por dia.

Etapa 2: O problema é maximizar$R.$

Etapa 3: A receita (por dia) é igual ao número de carros alugados por dia vezes o preço cobrado por carro por dia, ou seja,$R=n×p.$

Etapa 4: Como o número de carros alugados por dia é modelado pela função linear,$n(p)=1000−5p,$ a receita$R$ pode ser representada pela função

\[ \begin{align*} R(p) &=n×p \\[4pt] &=(1000−5p)p \\[4pt] &=−5p^2+1000p.\end{align*}\]

Etapa 5: Como os proprietários planejam cobrar entre$$50$ por carro$$200$ por dia e por carro por dia, o problema é encontrar a receita$R(p)$ máxima$p$ no intervalo fechado$[50,200]$.

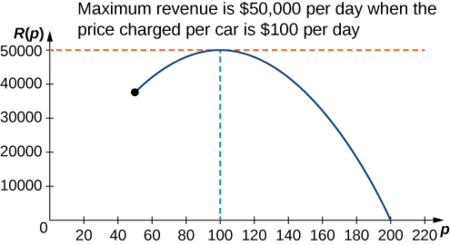
Etapa 6: Como$R$ é uma função contínua sobre o intervalo fechado e limitado$[50,200]$, ela tem um máximo absoluto (e um mínimo absoluto) nesse intervalo. Para encontrar o valor máximo, procure pontos críticos. A derivada é$R′(p)=−10p+1000.$ Portanto, o ponto crítico é$p=100$. Quando e$p=100, R(100)=$50,000.$ quando$p=50, R(p)=$37,500$. Quando$p=200, R(p)=$0$.

Portanto, o máximo absoluto ocorre em$p=$100$. A locadora de veículos deve cobrar$$100$ por dia por carro para maximizar a receita, conforme mostrado na figura a seguir.

A função R (p) é representada graficamente. No máximo, há uma interseção de duas linhas tracejadas e um texto que diz “A receita máxima é de $50.000 por dia quando o preço cobrado por carro é de $100 por dia”. — Figura$\PageIndex{6}$: Para maximizar a receita, uma locadora de veículos precisa equilibrar o preço de um aluguel com o número de carros que as pessoas alugarão por esse preço.

Exercício$\PageIndex{4}$

Uma locadora de veículos cobra$p$ dólares de seus clientes por dia, onde$60≤p≤150$. Ele descobriu que o número de carros alugados por dia pode ser modelado pela função linear.$n(p)=750−5p.$ Quanto a empresa deve cobrar de cada cliente para maximizar a receita?

Dica: $R(p)=n×p,$onde$n$ está o número de carros alugados e$p$ é o preço cobrado por carro.

Responda: A empresa deve cobrar$$75$ por carro por dia.

Exemplo$\PageIndex{5}$: Maximizing the Area of an Inscribed Rectangle

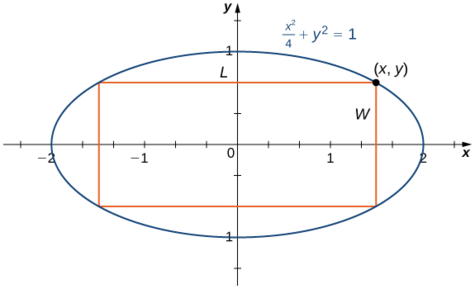
Um retângulo deve ser inscrito na elipse

\[\dfrac{x^2}{4}+y^2=1. \nonumber \]

Quais devem ser as dimensões do retângulo para maximizar sua área? Qual é a área máxima?

Solução

Etapa 1: Para que um retângulo seja inscrito na elipse, os lados do retângulo devem estar paralelos aos eixos. $L$Seja o comprimento do retângulo e$W$ sua largura. $A$Seja a área do retângulo.

A elipse x2/4 + y2 = 1 é desenhada com suas interceptações x sendo ±2 e suas interceptações y sendo ±1. Há um retângulo inscrito na elipse com comprimento L (na direção x) e largura W. — Figura$\PageIndex{7}$: Queremos maximizar a área de um retângulo inscrito em uma elipse.

Etapa 2: O problema é maximizar$A$.

Etapa 3: A área do retângulo é$A=LW.$

Etapa 4:$(x,y)$ Seja o canto do retângulo que fica no primeiro quadrante, conforme mostrado na Figura$\PageIndex{7}$. Podemos escrever comprimento$L=2x$ e largura$W=2y$. Desde$\dfrac{x^2}{4}+y^2=1$ e$y>0$, nós temos$y=\sqrt{1-\dfrac{x^2}{4}}$. Portanto, a área é

$A=LW=(2x)(2y)=4x\sqrt{1-\dfrac{x^2}{4}}=2x\sqrt{4−x^2}$

Etapa 5: Na Figura$\PageIndex{7}$, vemos que para inscrever um retângulo na elipse, a$x$ coordenada -do canto no primeiro quadrante deve ser satisfeita$0<x<2$. Portanto, o problema se reduz a procurar o valor máximo de$A(x)$ over the open interval$(0,2)$. Como$A(x)$ terá um máximo absoluto (e um mínimo absoluto) sobre o intervalo fechado$[0,2]$, consideramos$A(x)=2x\sqrt{4−x^2}$ sobre o intervalo$[0,2]$. Se o máximo absoluto ocorrer em um ponto interno, então encontramos um máximo absoluto no intervalo aberto.

Etapa 6: Como mencionado anteriormente,$A(x)$ é uma função contínua sobre o intervalo fechado e limitado$[0,2]$. Portanto, ele tem um máximo absoluto (e um mínimo absoluto). Nos pontos finais$x=0$ e$x=2$,$A(x)=0.$ Para$0<x<2$,$A(x)>0$.

Portanto, o máximo deve ocorrer em um ponto crítico. Tomando a derivada de$A(x)$, obtemos

\[ \begin{align*} A'(x) &=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x) \\[4pt] &=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}} \\[4pt] &=\dfrac{8−4x^2}{\sqrt{4−x^2}} . \end{align*}\]

Para encontrar pontos críticos, precisamos descobrir onde$A'(x)=0.$ podemos ver que if$x$ é uma solução de

\[\dfrac{8−4x^2}{\sqrt{4−x^2}}=0, \label{ex5eq1} \]

então$x$ deve satisfazer

\[8−4x^2=0. \nonumber \]

Portanto,$x^2=2.$ assim,$x=±\sqrt{2}$ são as possíveis soluções da Equação\ ref {ex5eq1}. Como estamos considerando$x$ ao longo do intervalo$[0,2]$,$x=\sqrt{2}$ existe a possibilidade de um ponto crítico, mas não$x=−\sqrt{2}$ é. Portanto, verificamos se$\sqrt{2}$ é uma solução da Equação\ ref {ex5eq1}. Como$x=\sqrt{2}$ é uma solução da Equação\ ref {ex5eq1}, concluímos que$\sqrt{2}$ é o único ponto crítico do intervalo$[0,2]$.$A(x)$

Portanto,$A(x)$ deve ter um máximo absoluto no ponto crítico$x=\sqrt{2}$. Para determinar as dimensões do retângulo, precisamos encontrar o comprimento$L$ e a largura$W$. Se$x=\sqrt{2}$ então

\[y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\nonumber \]

Portanto, as dimensões do retângulo são$L=2x=2\sqrt{2}$$W=2y=\dfrac{2}{\sqrt{2}}=\sqrt{2}$ e. A área desse retângulo é$ A=LW=(2\sqrt{2})(\sqrt{2})=4.$

Exercício$\PageIndex{5}$

Modifique a função de área$A$ se o retângulo for inscrito no círculo unitário$x^2+y^2=1$. Qual é o domínio de consideração?

Dica: Se$(x,y)$ for o vértice do quadrado que está no primeiro quadrante, então a área do quadrado é$A=(2x)(2y)=4xy.$

Responda: $A(x)=4x\sqrt{1−x^2}.$O domínio de consideração é$[0,1]$.

Resolvendo problemas de otimização quando o intervalo não está fechado ou não tem limites

Nos exemplos anteriores, consideramos funções em domínios fechados e limitados. Consequentemente, pelo teorema do valor extremo, tínhamos a garantia de que as funções tinham extrema absoluta. Vamos agora considerar funções para as quais o domínio não é fechado nem limitado.

Muitas funções ainda têm pelo menos um extremo absoluto, mesmo que o domínio não esteja fechado ou o domínio seja ilimitado. Por exemplo, a função$f(x)=x^2+4$ over$(−∞,∞)$ tem um mínimo absoluto de$4$ at$x=0$. Portanto, ainda podemos considerar funções sobre domínios ilimitados ou intervalos abertos e determinar se eles têm algum extremo absoluto. No próximo exemplo, tentaremos minimizar uma função em um domínio ilimitado. Veremos que, embora o domínio de consideração seja,$(0,∞),$ a função tem um mínimo absoluto.

No exemplo a seguir, analisamos a construção de uma caixa com a menor área de superfície com um volume prescrito. Não é difícil mostrar que, para uma caixa com tampa fechada, por simetria, entre todas as caixas com um volume especificado, um cubo terá a menor área de superfície. Consequentemente, consideramos o problema modificado de determinar qual caixa aberta com um volume especificado tem a menor área de superfície.

Exemplo$\PageIndex{6}$: Minimizing Surface Area

Uma caixa retangular com uma base quadrada, uma parte superior aberta e um volume de$216 \,\text{in}^3$ deve ser construída. Quais devem ser as dimensões da caixa para minimizar a área da superfície da caixa? Qual é a área mínima da superfície?

Solução

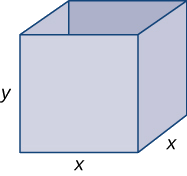
Etapa 1: Desenhe uma caixa retangular e introduza a variável$x$ para representar o comprimento de cada lado da base quadrada; vamos$y$ representar a altura da caixa. Deixe$S$ indicar a área da superfície da caixa aberta.

Uma caixa com base quadrada é mostrada. A base tem o comprimento lateral x e a altura é y. — Figura$\PageIndex{8}$: Queremos minimizar a área de superfície de uma caixa quadrada com um determinado volume.

Etapa 2: Precisamos minimizar a área da superfície. Portanto, precisamos minimizar$S$.

Etapa 3: Como a caixa tem uma parte superior aberta, precisamos apenas determinar a área dos quatro lados verticais e da base. A área de cada um dos quatro lados verticais é$x⋅y.$ A área da base é$x^2$. Portanto, a área da superfície da caixa é

$S=4xy+x^2$.

Etapa 4: Como o volume dessa caixa é$x^2y$ e o volume é dado como$216\,\text{in}^3$, a equação de restrição é

$x^2y=216$.

Resolvendo a equação de restrição para$y$, temos$y=\dfrac{216}{x^2}$. Portanto, podemos escrever a área da superfície em função$x$ apenas de:

\[S(x)=4x\left(\dfrac{216}{x^2}\right)+x^2.\nonumber \]

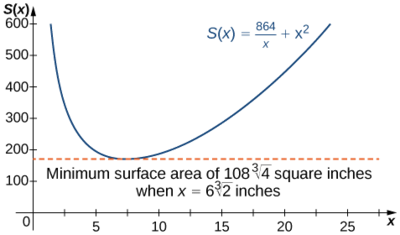
Portanto,$S(x)=\dfrac{864}{x}+x^2$.

Etapa 5: Como estamos exigindo isso$x^2y=216$, não podemos ter$x=0$. Portanto, precisamos$x>0$. Por outro lado,$x$ é permitido ter qualquer valor positivo. Observe que, à medida que$x$ se torna grande, a altura da caixa$y$ se torna correspondentemente pequena, de modo que$x^2y=216$. Da mesma forma, quando$x$ se torna pequena, a altura da caixa se torna correspondentemente grande. Concluímos que o domínio é o intervalo aberto e ilimitado$(0,∞)$. Observe que, diferentemente dos exemplos anteriores, não podemos reduzir nosso problema à procura de um máximo absoluto ou mínimo absoluto em um intervalo fechado e limitado. No entanto, na próxima etapa, descobrimos por que essa função deve ter um mínimo absoluto no intervalo$(0,∞).$

Etapa 6: Observe que, como$x→0^+,\, S(x)→∞.$ também, como$x→∞, \,S(x)→∞$. Como$S$ é uma função contínua que se aproxima do infinito nas extremidades, ela deve ter um mínimo absoluto em algumas$x∈(0,∞)$. Esse mínimo deve ocorrer em um ponto crítico de$S$. A derivada é

\[S′(x)=−\dfrac{864}{x^2}+2x.\nonumber \]

Portanto,$S′(x)=0$ quando$2x=\dfrac{864}{x^2}$. Resolvendo essa equação para$x$, obtemos$x^3=432$, então$x=\sqrt[3]{432}=6\sqrt[3]{2}.$ Como esse é o único ponto crítico de$S$, o mínimo absoluto deve ocorrer em$x=6\sqrt[3]{2}$ (veja a Figura$\PageIndex{9}$).

Quando$x=6\sqrt[3]{2}$,$y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}\,\text{in.}$ portanto, as dimensões da caixa devem ser$x=6\sqrt[3]{2}\,\text{in.}$ e$y=3\sqrt[3]{2}\,\text{in.}$ Com essas dimensões, a área da superfície é

\[S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}\,\text{in}^2\nonumber \]

A função S (x) = 864/x + x2 é representada graficamente. No mínimo, há uma linha tracejada e um texto que diz “A área mínima da superfície é 108 vezes a raiz cúbica de 4 polegadas quadradas quando x = 6 vezes a raiz cúbica de 2 polegadas”. — Figura$\PageIndex{9}$: Podemos usar um gráfico para determinar as dimensões de uma caixa com base no volume e na área mínima da superfície.

Exercício$\PageIndex{6}$

Considere a mesma caixa aberta, que deve ter volume$216\,\text{in}^3$. Suponha que o custo do material para a base seja$20¢/\text{in}^2$ e o custo do material para as laterais$30¢/\text{in}^2$ e estejamos tentando minimizar o custo dessa caixa. Escreva o custo em função dos comprimentos laterais da base. ($x$Seja o comprimento lateral da base e$y$ a altura da caixa.)

Dica: Se o custo de um dos lados for,$30¢/\text{in}^2,$ o custo desse lado é em$0.30xy$ dólares.

Responda: $c(x)=\dfrac{259.2}{x}+0.2x^2$dólares

Conceitos-chave

Para resolver um problema de otimização, comece desenhando uma imagem e introduzindo variáveis.
Encontre uma equação relacionando as variáveis.
Encontre uma função de uma variável para descrever a quantidade que deve ser minimizada ou maximizada.
Procure pontos críticos para localizar os extremos locais.

Glossário

problemas de otimização: problemas que são resolvidos ao encontrar o valor máximo ou mínimo de uma função

Exemplo\(\PageIndex{1}\): Maximizing the Area of a Garden

Exercício\(\PageIndex{1}\)

Estratégia de resolução de problemas: resolvendo problemas de otimização

Exemplo\(\PageIndex{2}\): Maximizing the Volume of a Box

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\): Minimizing Travel Time

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\): Maximizing Revenue

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\): Maximizing the Area of an Inscribed Rectangle

Exercício\(\PageIndex{5}\)

Exemplo\(\PageIndex{6}\): Minimizing Surface Area

Exercício\(\PageIndex{6}\)