4.7E: Exercícios para a Seção 4.7

Last updated
Save as PDF

Page ID: 188240

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para os exercícios 1 a 4, responda por prova, contra-exemplo ou explicação.

1) Quando você encontra o máximo para um problema de otimização, por que você precisa verificar o sinal da derivada em torno dos pontos críticos?

Resposta: Os pontos críticos podem ser os mínimos, os máximos ou nenhum deles.

2) Por que você precisa verificar se há problemas de otimização nos endpoints?

3) Verdadeiro ou falso. Para cada função não linear contínua, você pode encontrar o valor$x$ que maximiza a função.

Resposta: Falso;$y=−x^2$ tem apenas um mínimo

4) Verdadeiro ou falso. Para cada função contínua não constante em um domínio fechado e finito, existe pelo menos uma$x$ que minimiza ou maximiza a função.

Nos exercícios 5 a 8, configure e avalie cada problema de otimização.

5) Para transportar uma mala em um avião, a$\text{length}+\text{width}+\text{height}$ parte da caixa deve ser menor ou igual a$62$ dentro. Supondo que a altura seja fixa, mostre que o volume máximo é$V=h\left(31−\frac{1}{2}h\right)^2.$ Qual altura permite que você tenha o maior volume?

Resposta: $h=\frac{62}{3}$em.

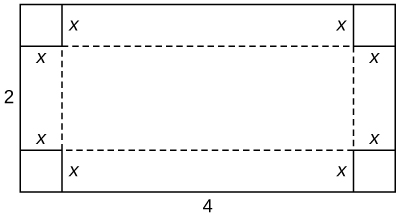
6) Você está construindo uma caixa de papelão com as dimensões$2$$4$ m por m. Em seguida, corta quadrados de tamanho igual em cada canto para poder dobrar as bordas. Quais são as dimensões da caixa com maior volume?

$Um retângulo é desenhado com altura 2 e largura 4. Cada canto tem um quadrado com o comprimento lateral x marcado nele.$

7) Encontre o inteiro positivo que minimiza a soma do número e seu recíproco.

Resposta: $1$

8) Encontre dois números inteiros positivos de forma que sua soma seja$10$, e minimize e maximize a soma de seus quadrados.

Nos exercícios 9 a 11, considere a construção de uma caneta para delimitar uma área.

9) Você tem$400\,\text{ft}$ uma cerca para construir uma caneta retangular para gado. Quais são as dimensões da caneta que maximizam a área?

Resposta: $100\,\text{ft}$por$100\,\text{ft}$

10) Você tem$800\,\text{ft}$ de esgrima para fazer uma caneta para porcos. Se você tem um rio em um lado de sua propriedade, qual é a dimensão da caneta retangular que maximiza a área?

11) Você precisa construir uma cerca em torno de uma área de$1600\,\text{ft}^2$. Quais são as dimensões da caneta retangular para minimizar a quantidade de material necessário?

Resposta: $40\,\text{ft}$por$40\,\text{ft}$

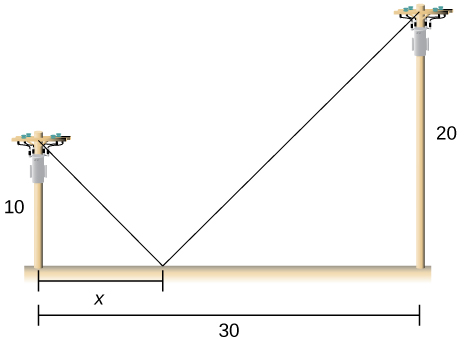
12) Dois pólos são conectados por um fio que também está conectado ao solo. O primeiro poste é$20\,\text{ft}$ alto e o segundo poste é$10\,\text{ft}$ alto. Há uma distância$30\,\text{ft}$ entre os dois pólos. Onde o fio deve ser ancorado ao solo para minimizar a quantidade de fio necessária?

$Dois postes são mostrados, um com 10 de altura e o outro com 20 de altura. Um triângulo reto é feito com o poste mais curto com outro lado de comprimento x. A distância entre os dois pólos é 30.$

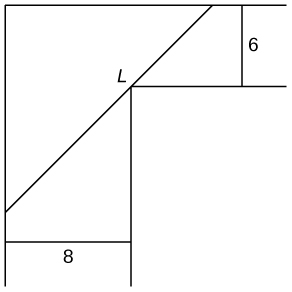
13) [T] Você está se mudando para um novo apartamento e percebe que há um canto onde o corredor se estreita$8\,\text{ft}$ para$6\,\text{ft}$. Qual é o comprimento do item mais longo que pode ser carregado horizontalmente na esquina?

$Uma figura ascendente em forma de L é desenhada com a parte _ tendo 6 de largura e a parte | com 8 de largura. Há uma linha traçada da parte _ até a parte | que toca o canto próximo da forma para formar uma hipotenusa para um triângulo reto, sendo os outros lados o resto das partes _ e |. Esta linha está marcada com L.$

Resposta: $19.73\,\text{ft}$

14) O pulso de um paciente mede$70 \,\text{bpm},\, 80 \,\text{bpm}$, então$120 \,\text{bpm}$. Para determinar uma medição precisa do pulso, o médico quer saber qual valor minimiza a expressão$(x−70)^2+(x−80)^2+(x−120)^2$? Qual valor o minimiza?

15) No problema anterior, suponha que o paciente estivesse nervoso durante a terceira medição, então pesamos esse valor apenas pela metade do que os outros. Qual é o valor que minimiza$(x−70)^2+ (x−80)^2+\frac{1}{2}(x−120)^2?$

Resposta: $84 \,\text{bpm}$

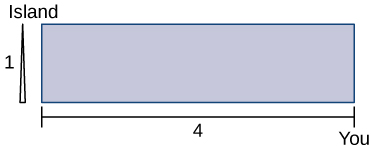
16) Você pode correr a uma velocidade de$6$ mph e nadar a uma velocidade de$3$ mph e está localizado na costa,$4$ milhas a leste de uma ilha que fica a$1$ milhas ao norte da costa. Até onde você deve correr para oeste para minimizar o tempo necessário para chegar à ilha?

$É desenhado um retângulo com altura 1 e comprimento 4. No canto inferior direito, está marcado com “Você” e no canto superior esquerdo está marcado como “Ilha”.$

Para os exercícios 17 a 19, considere um salva-vidas em uma piscina circular com diâmetro$40$ m. Ele deve alcançar alguém que esteja se afogando exatamente no lado oposto da piscina, na posição$C$. O salva-vidas nada com velocidade$v$ e corre pela piscina em alta velocidade$w=3v.$

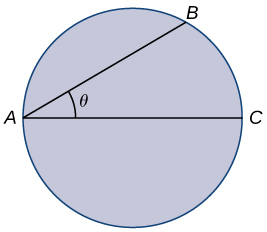
$Um círculo é desenhado com os pontos A e C em um diâmetro. Há um ponto B desenhado no círculo de forma que o ângulo BAC forme um ângulo agudo θ.$

17) Encontre uma função que meça o tempo total necessário para alcançar a pessoa que está se afogando em função do ângulo de natação,$θ$.

Resposta: $T(θ)=\dfrac{40θ}{3v}+\dfrac{40\cos θ}{v}$

18) Descubra em que ângulo$θ$ o salva-vidas deve nadar para alcançar a pessoa que está se afogando no menor tempo possível.

19) Um caminhão usa gás como$g(v)=av+\dfrac{b}{v}$, onde$v$ representa a velocidade do caminhão e$g$ representa os galões de combustível por milha. Em que velocidade o consumo de combustível é minimizado?

Resposta: $v=\sqrt{\dfrac{b}{a}}$

Para os exercícios 20 a 21, considere uma limusine que fica$m(v)=\frac{120−2v}{5}\,\text{mi/gal}$ em alta velocidade$v$, os custos$$15/\text{h}$ do motorista e a gasolina está$$3.50/\text{gal}$.

20) Encontre o custo por milha em alta velocidade$v.$

21) Encontre a velocidade de condução mais barata.

Resposta: aproximadamente$34.02$ mph

Para os exercícios 22 a 24, considere uma pizzaria que vende pizzas por uma receita$R(x)=ax$ e custos$C(x)=b+cx+dx^2$, onde$x$ representa o número de pizzas.

22) Encontre a função de lucro para o número de pizzas. Quantas pizzas dão o maior lucro por pizza?

23) Suponha que$R(x)=10x$$C(x)=2x+x^2$ e. Quantas pizzas vendidas maximizam o lucro?

Resposta: A venda de$4$ pizzas maximizará o lucro.

24) Suponha que$R(x)=15x$,$C(x)=60+3x+\frac{1}{2}x^2$ e. Quantas pizzas vendidas maximizam o lucro?

Para os exercícios 25 a 26, considere um fio$4$ de comprimento cortado em duas partes. Uma peça forma um círculo com raio$r$ e a outra forma um quadrado de lado$x$.

25)$x$ Opte por maximizar a soma de suas áreas.

Resposta: $x = 0$

26)$x$ Opte por minimizar a soma de suas áreas.

Para os exercícios 27 a 30, considere dois números não negativos$x$ e$y$ tal$x+y=10$. Maximize e minimize as quantidades.

27)$xy$

Resposta: Máximo:$x=5,\,y=5;$
Mínimo:$x=0,\,y=10$ e$y=0,\,x=10$

28$x^2y^2$

29)$y−\dfrac{1}{x}$

Resposta: Máximo:$x=1,\,y=9;$
Mínimo: nenhum

30)$x^2−y$

Nos exercícios 31 a 36, desenhe o problema de otimização fornecido e resolva.

31) Encontre o volume do maior cilindro circular reto que cabe em uma esfera de raio$1$.

Resposta: $V = \frac{4π}{3\sqrt{3}}$

32) Encontre o volume do maior cone direito que cabe em uma esfera de raio$1$.

33) Encontre a área do maior retângulo que se encaixa no triângulo com lados$x=0,\,y=0$ e$\dfrac{x}{4}+\dfrac{y}{6}=1.$

Resposta: $A = 6$

34) Encontre o maior volume de um cilindro que se encaixa em um cone com raio base$R$ e altura$h$.

35) Encontre as dimensões do volume do cilindro fechado$V=16π$ que tem a menor quantidade de área de superfície.

Resposta: $r=2,\,h=4$

36) Encontre as dimensões de um cone direito com a área de superfície$S=4π$ que tenha o maior volume.

Para os exercícios 37 a 40, considere os pontos nos gráficos das equações dadas. Use uma calculadora para representar graficamente as funções.

37) [T] Onde está a linha$y=5−2x$ mais próxima da origem?

Resposta: $(2,1)$

38) [T] Onde está a linha$y=5−2x$ mais próxima do ponto$(1,1)$?

39) [T] Onde está a parábola$y=x^2$ mais próxima do ponto$(2,0)$?

Resposta: $(0.8351,0.6974)$

40) [T] Onde está a parábola$y=x^2$ mais próxima do ponto$(0,3)$?

Nos exercícios 41 a 45, configure, mas não avalie, cada problema de otimização.

41) Uma janela é composta por um semicírculo colocado em cima de um retângulo. Se você tiver materiais$20\,\text{ft}$ de moldura de janela para a moldura externa, qual é o tamanho máximo da janela que você pode criar? Use r para representar o raio do semicírculo.

$Uma janela semicircular é desenhada com raio r.$

Resposta: $A=20r−2r^2−\frac{1}{2}πr^2$

42) Você tem uma fileira de plantas de$20$ melancia que produzem uma média de$30$ melancias cada. Para qualquer planta adicional de melancia plantada, a produção por planta de melancia cai em uma melancia. Quantas plantas extras de melancia você deve plantar?

43) Você está construindo uma caixa para seu gato dormir. O material de pelúcia para o fundo quadrado da caixa custa$$5/\text{ft}^2$ e o material para as laterais$$2/\text{ft}^2$. Você precisa de uma caixa com volume$4\,\text{ft}^3$. Encontre as dimensões da caixa que minimizam os custos. Use$x$ para representar o comprimento da lateral da caixa.

Resposta: $C(x)=5x^2+\dfrac{32}{x}$

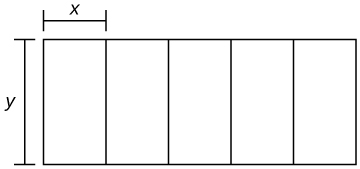
44) Você está construindo cinco canetas idênticas adjacentes uma à outra com uma área total de$1000\,\text{m}^2$, conforme mostrado na figura a seguir. Quais dimensões você deve usar para minimizar a quantidade de cercas?

$Um retângulo é dividido em cinco seções, e cada seção tem comprimento y e largura x.$

45) Você é o gerente de um complexo de apartamentos com$50$ unidades. Quando você define o aluguel em$$800/\text{month}$, todos os apartamentos são alugados. À medida que você aumenta o aluguel$$25/\text{month}$, um apartamento a menos é alugado. Os custos de manutenção são$$50/\text{month}$ cobrados para cada unidade ocupada. Qual é o aluguel que maximiza o valor total do lucro?

Resposta: $P(x)=(50−x)(800+25x−50)$