4.6E: Exercícios para a Seção 4.6

Last updated
Save as PDF

Page ID: 188366

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para os exercícios 1 a 5, examine os gráficos. Identifique onde as assíntotas verticais estão localizadas.

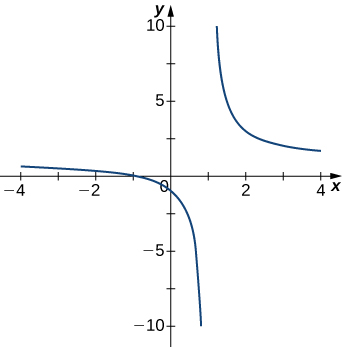
$A função representada graficamente diminui muito rapidamente à medida que se aproxima de x = 1 pela esquerda e, do outro lado de x = 1, parece começar perto do infinito e depois diminuir rapidamente.$

Resposta: $x=1$

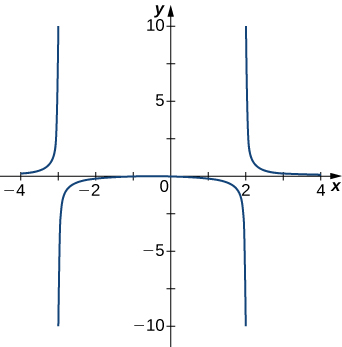
$A função representada graficamente aumenta muito rapidamente à medida que se aproxima de x = −3 pela esquerda e, do outro lado de x = −3, parece começar perto do infinito negativo e depois aumentar rapidamente para formar uma espécie de forma de U apontando para baixo, com o outro lado do U em x = 2. Do outro lado de x = 2, o gráfico parece começar perto do infinito e depois diminuir rapidamente.$

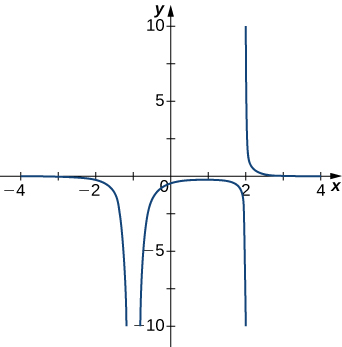
$A função representada graficamente diminui muito rapidamente à medida que se aproxima de x = −1 pela esquerda e, do outro lado de x = −1, parece começar perto do infinito negativo e depois aumentar rapidamente para formar uma espécie de forma de U apontando para baixo, com o outro lado do U em x = 2. Do outro lado de x = 2, o gráfico parece começar perto do infinito e depois diminuir rapidamente.$

Resposta: $x=−1,\;x=2$

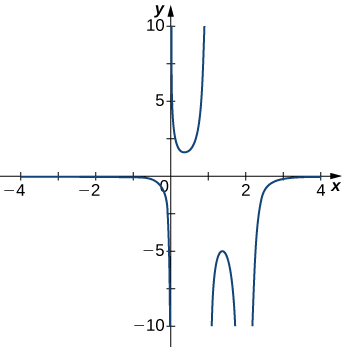
$A função representada graficamente diminui muito rapidamente à medida que se aproxima de x = 0 pela esquerda e, do outro lado de x = 0, parece começar perto do infinito e depois diminuir rapidamente para formar uma espécie de forma de U que está apontando para cima, com o outro lado do U em x = 1. Do outro lado de x = 1, há outra forma de U apontando para baixo, com o outro lado em x = 2. Do outro lado de x = 2, o gráfico parece começar perto do infinito negativo e depois aumentar rapidamente.$

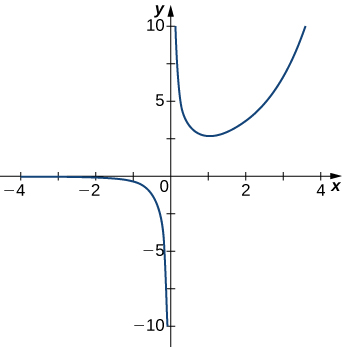
$A função representada graficamente diminui muito rapidamente à medida que se aproxima de x = 0 pela esquerda e, do outro lado de x = 0, parece começar perto do infinito e depois diminuir rapidamente para formar uma espécie de forma de U que está apontando para cima, com o outro lado sendo uma função normal que parece ocupar a totalidade do valores do eixo x.$

Resposta: $x=0$

Para as funções$f(x)$ dos exercícios 6 a 10, determine se há uma assíntota em$x=a$. Justifique sua resposta sem criar gráficos em uma calculadora.

6)$f(x)=\dfrac{x+1}{x^2+5x+4},\quad a=−1$

7)$f(x)=\dfrac{x}{x−2},\quad a=2$

Resposta: Sim, há uma assíntota vertical em$x = 2$.

8)$f(x)=(x+2)^{3/2},\quad a=−2$

9)$f(x)=(x−1)^{−1/3},\quad a=1$

Resposta: Sim, há assíntota vertical em$x = 1$.

10)$f(x)=1+x^{−2/5},\quad a=1$

Nos exercícios 11 a 20, avalie o limite.

11)$\displaystyle \lim_{x→∞}\frac{1}{3x+6}$

Resposta: $\displaystyle \lim_{x→∞}\frac{1}{3x+6} = 0$

12)$\displaystyle \lim_{x→∞}\frac{2x−5}{4x}$

13)$\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2}$

Resposta: $\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2} = ∞$

14)$\displaystyle \lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}$

15)$\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}$

Resposta: $\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4} = −\frac{1}{7}$

16)$\displaystyle \lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}$

17)$\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2}$

Resposta: $\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2} = -2$

18)$\displaystyle \lim_{x→∞}\frac{4x}{\sqrt{x^2−1}}$

19)$\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}}$

Resposta: $\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}} = -4$

20)$\displaystyle \lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}$

Para os exercícios 21 a 25, encontre as assíntotas horizontais e verticais.

21)$f(x)=x−\dfrac{9}{x}$

Resposta: Horizontal: nenhuma,
Vertical:$x=0$

22)$f(x)=\dfrac{1}{1−x^2}$

23)$f(x)=\dfrac{x^3}{4−x^2}$

Resposta: Horizontal: nenhuma,
Vertical:$x=±2$

24)$f(x)=\dfrac{x^2+3}{x^2+1}$

25)$f(x)=\sin(x)\sin(2x)$

Resposta: Horizontal: nenhuma,
Vertical: nenhuma

26)$f(x)=\cos x+\cos(3x)+\cos(5x)$

27)$f(x)=\dfrac{x\sin(x)}{x^2−1}$

Resposta: Horizontal:$y=0,$
Vertical:$x=±1$

28)$f(x)=\dfrac{x}{\sin(x)}$

29)$f(x)=\dfrac{1}{x^3+x^2}$

Resposta: Horizontal:$y=0,$
Vertical:$x=0$ e$x=−1$

30)$f(x)=\dfrac{1}{x−1}−2x$

31)$f(x)=\dfrac{x^3+1}{x^3−1}$

Resposta: Horizontal:$y=1,$
Vertical:$x=1$

32)$f(x)=\dfrac{\sin x+\cos x}{\sin x−\cos x}$

33)$f(x)=x−\sin x$

Resposta: Horizontal: nenhuma,
Vertical: nenhuma

34)$f(x)=\dfrac{1}{x}−\sqrt{x}$

Para os exercícios 35 a 38, construa uma função$f(x)$ que tenha as assíntotas dadas.

35)$x=1$ e$y=2$

Resposta: As respostas podem variar, por exemplo:$y=\dfrac{2x}{x−1}$

36)$x=1$ e$y=0$

37)$y=4, \;x=−1$

Resposta: As respostas podem variar, por exemplo:$y=\dfrac{4x}{x+1}$

38)$x=0$

Nos exercícios 39 a 43, represente graficamente a função em uma calculadora gráfica na janela$x=[−5,5]$ e estime a assíntota ou limite horizontal. Em seguida, calcule a assíntota ou o limite horizontal real.

39) [T]$f(x)=\dfrac{1}{x+10}$

Resposta: $\displaystyle \lim_{x→∞}\frac{1}{x+10}=0$então$f$ tem uma assíntota horizontal de$y=0$.

40) [T]$f(x)=\dfrac{x+1}{x^2+7x+6}$

41) [T]$\displaystyle \lim_{x→−∞}x^2+10x+25$

Resposta: $\displaystyle \lim_{x→−∞}x^2+10x+25 = ∞$

42) [T]$\displaystyle \lim_{x→−∞}\frac{x+2}{x^2+7x+6}$

43) [T]$\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}$

Resposta: $\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}=3$então essa função tem uma assíntota horizontal de$y=3$.

Nos exercícios 44 a 55, desenhe um gráfico das funções sem usar uma calculadora. Certifique-se de observar todas as características importantes do gráfico: máximos e mínimos locais, pontos de inflexão e comportamento assintótico.

44)$y=3x^2+2x+4$

45)$y=x^3−3x^2+4$

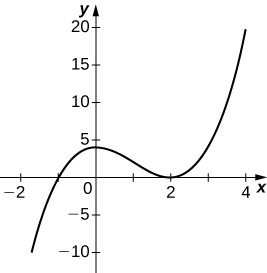
Resposta: $A função começa no terceiro quadrante, aumenta para passar por (−1, 0), aumenta até o máximo e o intercepto y em 4, diminui para o toque (2, 0) e depois aumenta para (4, 20).$

(46)$y=\dfrac{2x+1}{x^2+6x+5}$

47)$y=\dfrac{x^3+4x^2+3x}{3x+9}$

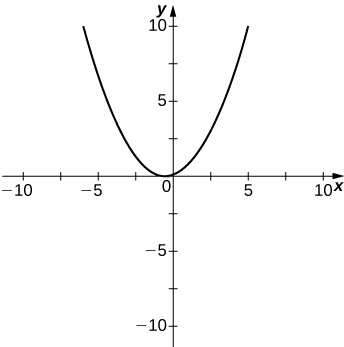
Resposta: $Uma parábola voltada para cima com o mínimo entre x = 0 e x = −1 com intercepto y entre 0 e 1.$

48)$y=\dfrac{x^2+x−2}{x^2−3x−4}$

49)$y=\sqrt{x^2−5x+4}$

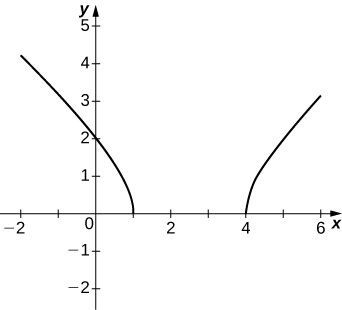
Resposta: $Esse gráfico começa em (−2, 4) e diminui de forma convexa para (1, 0). Em seguida, o gráfico começa novamente em (4, 0) e aumenta de forma convexa para (6, 3).$

50)$y=2x\sqrt{16−x^2}$

51)$y=\dfrac{\cos x}{x}$, não$x=[−2π,2π]$

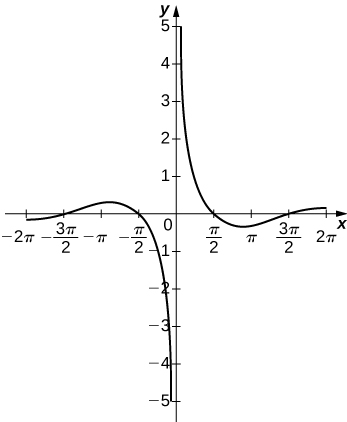
Resposta: $Este gráfico tem assíntota vertical em x = 0. A primeira parte da função ocorre no segundo e terceiro quadrantes e começa no terceiro quadrante logo abaixo (−2π, 0), aumenta e passa pelo eixo x em −3π /2, atinge um máximo e depois diminui pelo eixo x em −π /2 antes de se aproximar da assíntota. Do outro lado da assíntota, a função começa no primeiro quadrante, diminui rapidamente para passar por π /2, diminui para um mínimo local e depois aumenta (3π /2, 0) antes de ficar logo acima (2π, 0).$

52)$y=e^x−x^3$

53)$y=x\tan x, \quad x=[−π,π]$

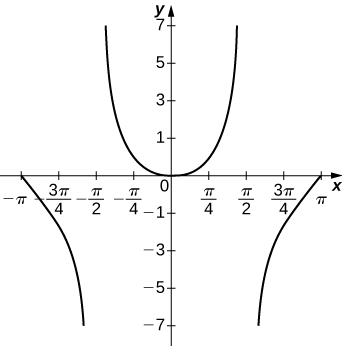
Resposta: $Este gráfico tem assíntotas verticais em x = ±π /2. O gráfico é simétrico em relação ao eixo y, portanto, descrever o lado esquerdo será suficiente. A função começa em (−π, 0) e diminui rapidamente para a assíntota. Em seguida, ele começa do outro lado da assíntota no segundo quadrante e diminui para a origem.$

54)$y=x\ln(x), \quad x>0$

55)$y=x^2\sin(x),\quad x=[−2π,2π]$

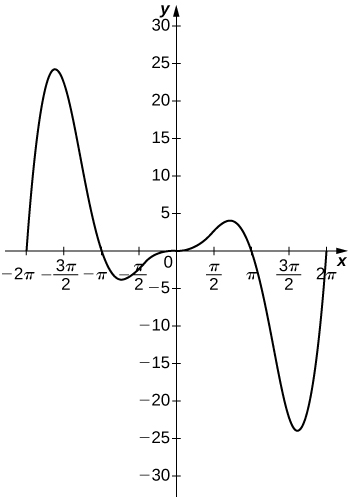
Resposta: $Essa função começa em (−2π, 0), aumenta para perto (−3π /2, 25), diminui até (−π, 0), atinge um mínimo local e depois aumenta através da origem. Do outro lado da origem, o gráfico é o mesmo, mas invertido, ou seja, é congruente com a outra metade por uma rotação de 180 graus.$

56)$f(x)=\dfrac{P(x)}{Q(x)}$ Para ter uma assíntota em$y=2$ seguida os polinômios$P(x)$ e$Q(x)$ deve ter qual relação?

57)$f(x)=\dfrac{P(x)}{Q(x)}$ Para ter uma assíntota em$x=0$, então os polinômios$P(x)$ e$Q(x).$ deve ter qual relação?

Resposta: $Q(x).$deve ter$x^{k+1}$ como fator, onde$P(x)$ tem$x^k$ como fator.

58) Se$f′(x)$ tem assíntotas em$y=3$ e$x=1$, então$f(x)$ tem quais assíntotas?

59) Ambos$f(x)=\dfrac{1}{x−1}$ e$g(x)=\dfrac{1}{(x−1)^2}$ têm assíntotas em$x=1$ e$y=0.$ Qual é a diferença mais óbvia entre essas duas funções?

Resposta: $\displaystyle \lim_{x→1^−}f(x)=-\infty \text{ and } \lim_{x→1^−}g(x)=\infty$

60) Verdadeiro ou falso: Cada proporção de polinômios tem assíntotas verticais.