4.6: Limites no infinito e nas assíntotas
- Page ID
- 188352
- Calcule o limite de uma função à medida que\(x\) aumenta ou diminui sem limite.
- Reconheça uma assíntota horizontal no gráfico de uma função.
- Estime o comportamento final de uma função à medida que\(x\) aumenta ou diminui sem limite.
- Reconheça uma assíntota oblíqua no gráfico de uma função.
- Analise uma função e suas derivadas para desenhar seu gráfico.
Mostramos como usar a primeira e a segunda derivadas de uma função para descrever a forma de um gráfico. Para representar graficamente uma função\(f\) definida em um domínio ilimitado, também precisamos conhecer o comportamento de\(f\) as\(x→±∞\). Nesta seção, definimos limites no infinito e mostramos como esses limites afetam o gráfico de uma função. No final desta seção, descrevemos uma estratégia para representar graficamente uma função arbitrária\(f\).
Começamos examinando o que significa para uma função ter um limite finito no infinito. Em seguida, estudamos a ideia de uma função com um limite infinito no infinito. De volta à Introdução às Funções e Gráficos, analisamos as assíntotas verticais; nesta seção, lidamos com assíntotas horizontais e oblíquas.
Limites no infinito e nas assíntotas horizontais
Lembre-se de que o\(\displaystyle \lim_{x→a}f(x)=L\) meio\(f(x)\) se torna arbitrariamente próximo\(L\), desde que\(x\) esteja suficientemente próximo de\(a\). Podemos estender essa ideia até limites no infinito. Por exemplo, considere a função\(f(x)=2+\frac{1}{x}\). Como pode ser visto graficamente na Figura\(\PageIndex{1}\) e numericamente na Tabela\(\PageIndex{1}\), à medida que os valores de\(x\) aumentam, os valores de\(f(x)\) aproximação\(2\). Dizemos que o limite se\(x\) aproxima\(∞\) do\(f(x)\) é\(2\) e escrevemos\(\displaystyle \lim_{x→∞}f(x)=2\). Da mesma forma\(x<0\), para, à medida\(|x|\) que os valores aumentam, os valores da\(f(x)\) abordagem\(2\). Dizemos que o limite se\(x\) aproxima\(−∞\) do\(f(x)\) é\(2\) e escrevemos\(\displaystyle \lim_{x→−∞}f(x)=2\).
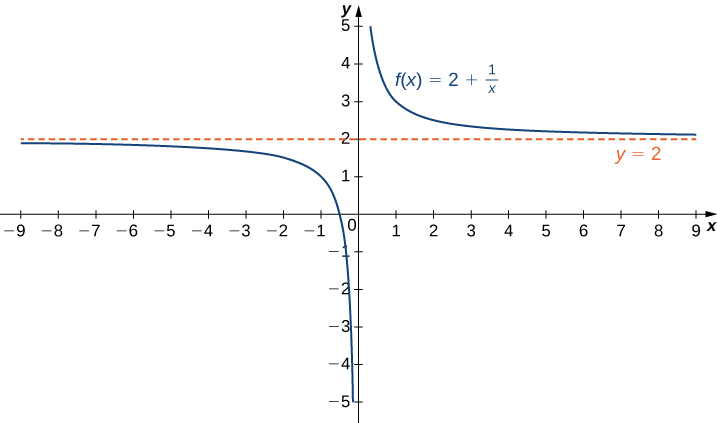
| \(x\) | 10 | 100 | 1.000 | 10.000 |
|---|---|---|---|---|
| \(2+\frac{1}{x}\) | 2.1 | 2,01 | 2.001 | 2.0001 |
| \(x\) | −10 | −100 | −1000 | −10.000 |
| \(2+\frac{1}{x}\) | 1.9 | 1,99 | 1.999 | 1.999 |
De forma mais geral, para qualquer função\(f\), dizemos que o limite a partir\(x→∞\) de\(f(x)\) é\(L\) se\(f(x)\) se torna arbitrariamente próximo do tempo que\(x\) for suficientemente grande.\(L\) Nesse caso, nós escrevemos\(\displaystyle \lim_{x→∞}f(x)=L\). Da mesma forma, dizemos que o limite a partir\(x→−∞\) de\(f(x)\) é\(L\) se\(f(x)\) se tornar arbitrariamente próximo de\(L\) tão longo quanto\(x<0\) e\(|x|\) for suficientemente grande. Nesse caso, nós escrevemos\(\displaystyle \lim_{x→−∞}f(x)=L\). Agora, examinamos a definição de uma função com um limite no infinito.
Se os valores de\(f(x)\) se tornarem arbitrariamente próximos de\(L\) as\(x\) se tornarem suficientemente grandes, dizemos que a função\(f\) tem um limite no infinito e escrevemos
\[\lim_{x→∞}f(x)=L. \nonumber \]
Se os valores de\(f(x)\) se tornarem arbitrariamente próximos de\(L\) for à\(x<0\) medida que\(|x|\) se tornam suficientemente grandes, dizemos que a função\(f\) tem um limite no infinito negativo e escrevemos
\[\lim_{x→−∞}f(x)=L. \nonumber \]
Se os valores\(f(x)\) estiverem se aproximando arbitrariamente de algum valor finito\(L\) como\(x→∞\) ou\(x→−∞\), o gráfico de\(f\) se aproxima da linha\(y=L\). Nesse caso, a linha\(y=L\) é uma assíntota horizontal de\(f\) (Figura\(\PageIndex{2}\)). Por exemplo, para a função\(f(x)=\dfrac{1}{x}\), uma vez que\(\displaystyle \lim_{x→∞}f(x)=0\), a linha\(y=0\) é uma assíntota horizontal de\(f(x)=\dfrac{1}{x}\).

Se\(\displaystyle \lim_{x→∞}f(x)=L\) ou\(\displaystyle \lim_{x→−∞}f(x)=L\), dizemos que a linha\(y=L\) é uma assíntota horizontal de\(f\).
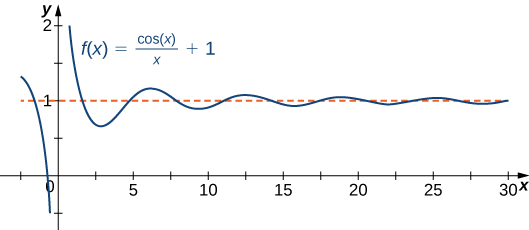
Uma função não pode cruzar uma assíntota vertical porque o gráfico deve se aproximar do infinito (ou\( −∞\)) de pelo menos uma direção quando\(x\) se aproxima da assíntota vertical. No entanto, uma função pode cruzar uma assíntota horizontal. Na verdade, uma função pode cruzar uma assíntota horizontal um número ilimitado de vezes. Por exemplo, a função\(f(x)=\dfrac{\cos x}{x}+1\) mostrada na Figura\(\PageIndex{3}\) cruza a assíntota horizontal\(y=1\) um número infinito de vezes à medida que ela oscila em torno da assíntota com amplitude cada vez menor.
As leis do limite algébrico e o teorema de compressão que introduzimos na Introdução aos Limites também se aplicam aos limites no infinito. Ilustramos como usar essas leis para calcular vários limites no infinito.
Para cada uma das seguintes funções\(f\),\(\displaystyle \lim_{x→∞}f(x)\) avalie\(\displaystyle \lim_{x→−∞}f(x)\) e. Determine a assíntota (s) horizontal (s) para\(f\).
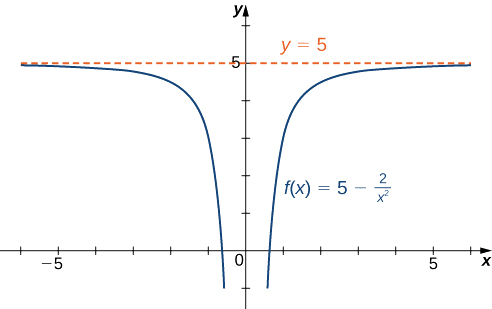
- \(f(x)=5−\dfrac{2}{x^2}\)
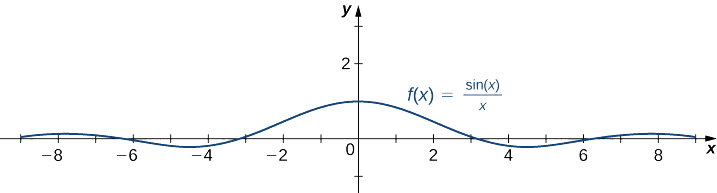
- \(f(x)=\dfrac{\sin x}{x}\)
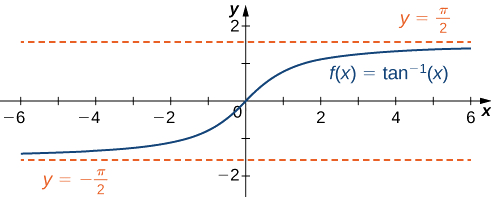
- \(f(x)=\tan^{−1}(x)\)
Solução
a. Usando as leis de limite algébricos, temos
\[\lim_{x→∞}\left(5−\frac{2}{x^2}\right)=\lim_{x→∞}5−2\left(\lim_{x→∞}\frac{1}{x}\right)\cdot\left(\lim_{x→∞}\frac{1}{x}\right)=5−2⋅0=5.\nonumber \]
Da mesma forma,\(\displaystyle \lim_{x→−∞}f(x)=5\). Portanto,\(f(x)=5-\dfrac{2}{x^2}\) tem uma assíntota horizontal\(y=5\) e\(f\) se aproxima dessa assíntota horizontal\(x→±∞\), conforme mostrado no gráfico a seguir.
b. Uma vez que,\(-1≤\sin x≤1\) para todos\(x\), temos
\[\frac{−1}{x}≤\frac{\sin x}{x}≤\frac{1}{x}\nonumber \]
para todos\(x≠0\). Além disso, uma vez que
\(\displaystyle \lim_{x→∞}\frac{−1}{x}=0=\lim_{x→∞}\frac{1}{x}\),
podemos aplicar o teorema da compressão para concluir que
\(\displaystyle \lim_{x→∞}\frac{\sin x}{x}=0.\)
Da mesma forma,
\(\displaystyle \lim_{x→−∞}\frac{\sin x}{x}=0.\)
Assim,\(f(x)=\dfrac{\sin x}{x}\) tem uma assíntota horizontal\(y=0\) e\(f(x)\) se aproxima dessa assíntota horizontal\(x→±∞\), conforme mostrado no gráfico a seguir.
c. Para avaliar\(\displaystyle \lim_{x→∞}\tan^{−1}(x)\) e\(\displaystyle \lim_{x→−∞}\tan^{−1}(x)\), primeiro consideramos o gráfico do\(y=\tan(x)\) intervalo,\(\left(−\frac{π}{2},\frac{π}{2}\right)\) conforme mostrado no gráfico a seguir.
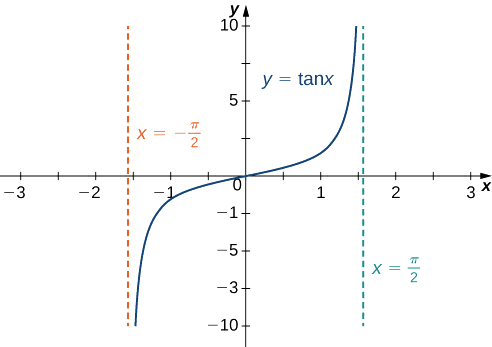
Desde
\(\displaystyle \lim_{x→\tfrac{π}{2}^−}\tan x=∞,\)
segue-se que
\(\displaystyle \lim_{x→∞}\tan^{−1}(x)=\frac{π}{2}.\)
Da mesma forma, já que
\(\displaystyle \lim_{x→-\tfrac{π}{2}^+}\tan x=−∞,\)
segue-se que
\(\displaystyle \lim_{x→−∞}\tan^{−1}(x)=−\frac{π}{2}.\)
Como resultado,\(y=\frac{π}{2}\) e\(y=−\frac{π}{2}\) são assíntotas horizontais\(f(x)=\tan^{−1}(x)\), conforme mostrado no gráfico a seguir.
Avalie\(\displaystyle \lim_{x→−∞}\left(3+\frac{4}{x}\right)\)\(\displaystyle \lim_{x→∞}\left(3+\dfrac{4}{x}\right)\) e. Determine as assíntotas horizontais de,\(f(x)=3+\frac{4}{x},\) se houver.
- Dica
-
\(\displaystyle \lim_{x→±∞}\frac{1}{x}=0\)
- Responda
-
Ambos os limites são\(3.\) A linha\(y=3\) é uma assíntota horizontal.
Limites infinitos no infinito
Às vezes, os valores de uma função\(f\) se tornam arbitrariamente grandes como\(x→∞ \) (ou como\(x→−∞\)). Nesse caso, escrevemos\(\displaystyle \lim_{x→∞}f(x)=∞\) (ou\(\displaystyle \lim_{x→−∞}f(x)=∞\)). Por outro lado, se os valores de\(f\) forem negativos, mas se tornarem arbitrariamente grandes em magnitude como\(x→∞\) (ou como\(x→−∞\)), escrevemos\(\displaystyle \lim_{x→∞}f(x)=−∞\) (ou\(\displaystyle \lim_{x→−∞}f(x)=−∞\)).
Por exemplo, considere a função\(f(x)=x^3\). Conforme visto na Tabela\(\PageIndex{2}\) e na Figura\(\PageIndex{8}\), à medida\(x→∞\) que os valores\(f(x)\) se tornam arbitrariamente grandes. Portanto,\(\displaystyle \lim_{x→∞}x^3=∞\). Por outro lado, como\(x→−∞\), os valores de\(f(x)=x^3\) são negativos, mas se tornam arbitrariamente grandes em magnitude. Consequentemente,\(\displaystyle \lim_{x→−∞}x^3=−∞.\)
| \(x\) | 10 | 20 | 50 | 100 | 1000 |
|---|---|---|---|---|---|
| \(x^3\) | 1000 | 8000 | 125.000 | 1.000.000 | 1.000.000.000 |
| \(x\) | −10 | −20 | −50 | −100 | −1000 |
| \(x^3\) | −1000 | −8000 | −125.000 | −1.000.000 | −1.000.000.000 |
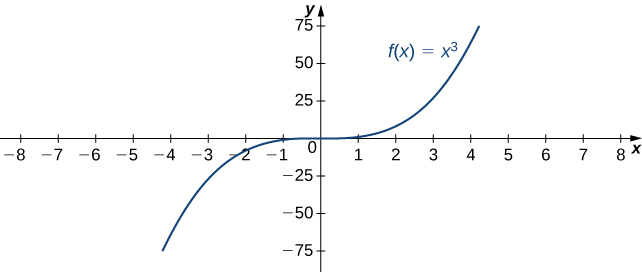
Dizemos que uma função\(f\) tem um limite infinito no infinito e escrevemos
\[\lim_{x→∞}f(x)=∞. \nonumber \]
se\(f(x)\) torna arbitrariamente grande para\(x\) suficientemente grande. Dizemos que uma função tem um limite infinito negativo no infinito e escrevemos
\[\lim_{x→∞}f(x)=−∞. \nonumber \]
se\(f(x)<0\) e\(|f(x)|\) se torna arbitrariamente grande para\(x\) suficientemente grande. Da mesma forma, podemos definir limites infinitos como\(x→−∞.\)
Definições formais
Anteriormente, usamos os termos arbitrariamente próximos, arbitrariamente grandes e suficientemente grandes para definir limites no infinito informalmente. Embora esses termos forneçam descrições precisas dos limites no infinito, eles não são precisos matematicamente. Aqui estão definições mais formais de limites no infinito. Em seguida, examinamos como usar essas definições para provar resultados envolvendo limites no infinito.
Dizemos que uma função\(f\) tem um limite no infinito, se existe um número real\(L\) tal que, para todos\(ε>0\), existe\(N>0\) tal que
\[|f(x)−L|<ε \nonumber \]
para todos,\(x>N.\) nesse caso, escrevemos
\[\lim_{x→∞}f(x)=L \nonumber \]
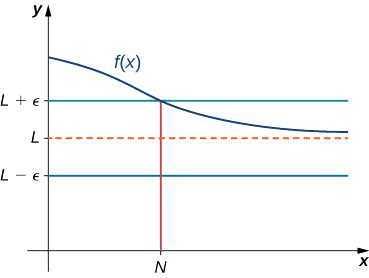
No início desta seção, usamos evidências gráficas na Figura\(\PageIndex{1}\) e evidências numéricas na Tabela\(\PageIndex{1}\) para concluir isso\(\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2\). Aqui usamos a definição formal de limite no infinito para provar esse resultado rigorosamente.
Use a definição formal de limite no infinito para provar isso\(\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2\).
Solução
Deixe,\(ε>0.\) deixe\(N=\frac{1}{ε}\). Portanto, para todos\(x>N\), temos
\[\left|2+\frac{1}{x}−2\right|=\left|\frac{1}{x}\right|=\frac{1}{x}<\frac{1}{N}=ε \nonumber \]
Use a definição formal de limite no infinito para provar isso\(\displaystyle \lim_{x→∞}\left(3-\frac{1}{x^2}\right)=3\).
- Dica
-
Deixe\(N=\frac{1}{\sqrt{ε}}\).
- Responda
-
Deixe,\(ε>0.\) deixe\(N=\frac{1}{\sqrt{ε}}\). Portanto, por tudo o\(x>N,\) que temos
\[\Big|3−\frac{1}{x^2}−3\Big|=\frac{1}{x^2}<\frac{1}{N^2}=ε \nonumber \]
Portanto,\(\displaystyle \lim_{x→∞}(3−1/x^2)=3.\)
Agora voltamos nossa atenção para uma definição mais precisa de um limite infinito no infinito.
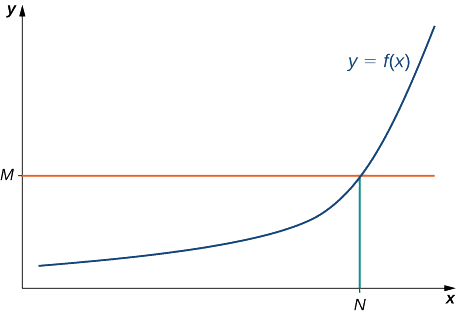
Dizemos que uma função\(f\) tem um limite infinito no infinito e escrevemos
\(\displaystyle \lim_{x→∞}f(x)=∞\)
se por todos\(M>0,\) existe um\(N>0\) tal que
\(f(x)>M\)
para todos\(x>N\) (veja a Figura\(\PageIndex{10}\)).
Dizemos que uma função tem um limite infinito negativo no infinito e escrevemos
\(\displaystyle \lim_{x→∞}f(x)=−∞\)
se para todos\(M<0\), existe um\(N>0\) tal que
\(f(x)<M\)
para todos\(x>N\).
Da mesma forma, podemos definir limites como\(x→−∞.\)
Anteriormente, usamos evidências gráficas (Figura\(\PageIndex{8}\)) e evidências numéricas (Tabela\(\PageIndex{2}\)) para concluir isso\(\displaystyle \lim_{x→∞}x^3=∞\). Aqui usamos a definição formal de limite infinito no infinito para provar esse resultado.
Use a definição formal de limite infinito no infinito para provar que\(\displaystyle \lim_{x→∞}x^3=∞.\)
Solução
Deixe,\(M>0.\) deixe\(N=\sqrt[3]{M}\). Então, para todos\(x>N\), temos
\(x^3>N^3=(\sqrt[3]{M})^3=M.\)
Portanto,\(\displaystyle \lim_{x→∞}x^3=∞\).
Use a definição formal de limite infinito no infinito para provar que\(\displaystyle \lim_{x→∞}3x^2=∞.\)
- Dica
-
Deixe\(N=\sqrt{\frac{M}{3}}\).
- Responda
-
Deixe,\(M>0.\) deixe\(N=\sqrt{\frac{M}{3}}\). Então, por tudo o\(x>N,\) que temos
\(3x^2>3N^2=3\left(\sqrt{\frac{M}{3}}\right)^2=\frac{3M}{3}=M\)
Comportamento final
O comportamento de uma função, como\(x→±∞\) é chamado de comportamento final da função. Em cada extremidade da função, a função pode exibir um dos seguintes tipos de comportamento:
- A função\(f(x)\) se aproxima de uma assíntota horizontal\(y=L\).
- A função\(f(x)→∞\) ou\(f(x)→−∞.\)
- A função não se aproxima de um limite finito, nem se aproxima de\(∞\) ou\(−∞\). Nesse caso, a função pode ter algum comportamento oscilatório.
Vamos considerar várias classes de funções aqui e ver os diferentes tipos de comportamentos finais dessas funções.
Comportamento final para funções polinomiais
Considere a função de potência\(f(x)=x^n\) onde\(n\) é um número inteiro positivo. De Figura\(\PageIndex{11}\) e Figura\(\PageIndex{12}\), vemos que
\[\lim_{x→∞}x^n=∞;\;n=1,2,3,… \nonumber \]
e
\[\lim_{x→−∞}x^n=\begin{cases}∞, & n=2,4,6,…\\−∞, & n=1,3,5,….\end{cases} \nonumber \]
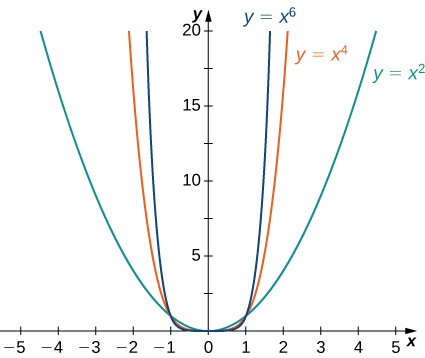
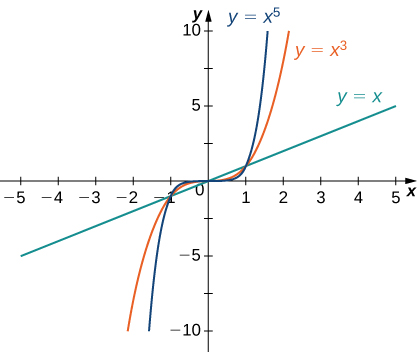
Usando esses fatos, não é difícil avaliar\(\displaystyle \lim_{x→∞}cx^n\) e\(\displaystyle \lim_{x→−∞}cx^n\), onde\(c\) há qualquer constante e\(n\) é um número inteiro positivo. Se\(c>0\), o gráfico de\(y=cx^n\) é um estiramento vertical ou compressão de\(y=x^n,\) e, portanto,
\(\displaystyle \lim_{x→∞}cx^n=\lim_{x→∞}x^n\)e\(\displaystyle \lim_{x→−∞}cx^n=\lim_{x→−∞}x^n\) se\(c>0\).
Se\(c<0,\) o gráfico de\(y=cx^n\) for um estiramento ou compressão vertical combinado com uma reflexão sobre o\(x\) eixo -e, portanto,
\(\displaystyle \lim_{x→∞}cx^n=−\lim_{x→∞}x^n\)e\(\displaystyle \lim_{x→−∞}cx^n=−\lim_{x→−∞}x^n\) se\(c<0.\)
Se\(c=0,y=cx^n=0,\) nesse caso\(\displaystyle \lim_{x→∞}cx^n=0=\lim_{x→−∞}cx^n.\)
Para cada função\(f\),\(\displaystyle \lim_{x→∞}f(x)\) avalie\(\displaystyle \lim_{x→−∞}f(x)\) e.
- \(f(x)=−5x^3\)
- \(f(x)=2x^4\)
Solução
- Como o coeficiente de\(x^3\) é\(−5\), o gráfico de\(f(x)=−5x^3\) envolve um estiramento vertical e uma reflexão do gráfico de\(y=x^3\) cerca do\(x\) eixo. Portanto,\(\displaystyle \lim_{x→∞}(−5x^3)=−∞\)\(\displaystyle \lim_{x→−∞}(−5x^3)=∞\) e.
- Como o coeficiente de\(x^4\) é\(2\), o gráfico de\(f(x)=2x^4\) é um trecho vertical do gráfico de\(y=x^4\). Portanto,\(\displaystyle \lim_{x→∞}2x^4=∞\)\(\displaystyle \lim_{x→−∞}2x^4=∞\) e.
Deixe\(f(x)=−3x^4\). Encontre\(\displaystyle \lim_{x→∞}f(x)\).
- Dica
-
O coeficiente\(−3\) é negativo.
- Responda
-
\(−∞\)
Agora, veremos como os limites no infinito para funções de potência podem ser usados\(\displaystyle \lim_{x→±∞}f(x)\) para determinar qualquer função polinomial\(f\). Considere uma função polinomial
\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a^1x+a^0 \nonumber \]
de grau\(n≥1\) para que\(a_n≠0.\)
Fatorando, vemos que
\[f(x)=a_nx^n\left(1+\frac{a_{n−1}}{a_n}\frac{1}{x}+…+\frac{a_1}{a_n}\frac{1}{x^{n−1}}+\frac{a_0}{a_n}\frac{1}{x^n}\right). \nonumber \]
Como\(x→±∞,\) todos os termos dentro dos parênteses se aproximam de zero, exceto o primeiro termo. Concluímos que
\[\lim_{x→±∞}f(x)=\lim_{x→±∞}a_nx^n. \nonumber \]
Por exemplo, a função\(f(x)=5x^3−3x^2+4\) se comporta\(g(x)=5x^3\)\(x→±∞\) como mostrado na Figura\(\PageIndex{13}\) e na Tabela\(\PageIndex{3}\).
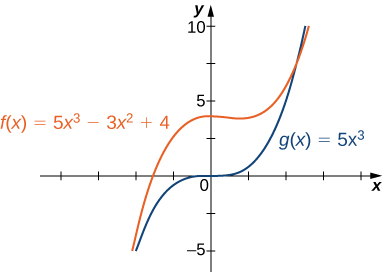
| \(x\) | 10 | 100 | 1000 |
|---|---|---|---|
| \(f(x)=5x^3−3x^2+4\) | 4704 | 4.970,004 | 4.997.000,004 |
| \(g(x)=5x^3\) | 5000 | 5.000.000 | 5.000.000.000 |
| \(x\) | −10 | −100 | −000 |
| \(f(x)=5x^3−3x^2+4\) | −5296 | −5.029.996 | −5.002.999.996 |
| \(g(x)=5x^3\) | −5000 | −5.000.000 | −5.000.000.000 |
Comportamento final para funções algébricas
O comportamento final para funções racionais e funções envolvendo radicais é um pouco mais complicado do que para polinômios. No exemplo\(\PageIndex{5}\), mostramos que os limites no infinito de uma função racional\(f(x)=\dfrac{p(x)}{q(x)}\) dependem da relação entre o grau do numerador e o grau do denominador. Para calcular os limites no infinito de uma função racional, dividimos o numerador e o denominador pela maior potência de\(x\) aparecer no denominador. Isso determina qual termo na expressão geral domina o comportamento da função em grandes valores de\(x\).
Para cada uma das funções a seguir, determine os limites como\(x→∞\) e,\(x→−∞.\) em seguida, use essas informações para descrever o comportamento final da função.
- \(f(x)=\dfrac{3x−1}{2x+5}\)(Nota: O grau do numerador e do denominador são os mesmos.)
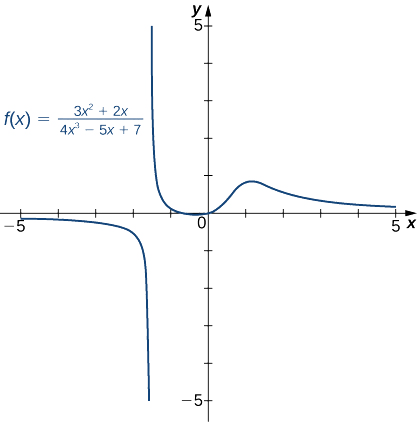
- \(f(x)=\dfrac{3x^2+2x}{4x^3−5x+7}\)(Nota: O grau do numerador é menor que o grau do denominador.)
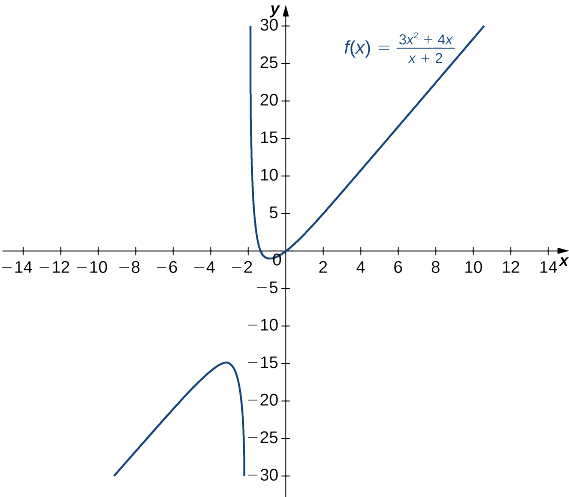
- \(f(x)=\dfrac{3x^2+4x}{x+2}\)(Nota: O grau do numerador é maior do que o grau do denominador.)
Solução
a. A maior potência de\(x\) no denominador é\(x\). Portanto, dividindo o numerador e o denominador\(x\) e aplicando as leis do limite algébrico, vemos que
\[ \begin{align*} \lim_{x→±∞}\frac{3x−1}{2x+5} &=\lim_{x→±∞}\frac{3−1/x}{2+5/x} \\[4pt] &=\frac{\lim_{x→±∞}(3−1/x)}{\lim_{x→±∞}(2+5/x)} \\[4pt] &=\frac{\lim_{x→±∞}3−\lim_{x→±∞}1/x}{\lim_{x→±∞}2+\lim_{x→±∞}5/x} \\[4pt] &=\frac{3−0}{2+0}=\frac{3}{2}. \end{align*}\]
Pois\(\displaystyle \lim_{x→±∞}f(x)=\frac{3}{2}\), sabemos que\(y=\frac{3}{2}\) é uma assíntota horizontal para essa função, conforme mostrado no gráfico a seguir.
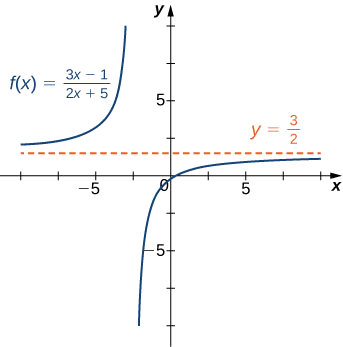
b. Como a maior potência de\(x\) aparecer no denominador é\(x^3\), divida o numerador e o denominador por\(x^3\). Depois de fazer isso e aplicar as leis de limite algébricos, obtemos
\[\lim_{x→±∞}\frac{3x^2+2x}{4x^3−5x+7}=\lim_{x→±∞}\frac{3/x+2/x^2}{4−5/x^2+7/x^3}=\frac{3\cdot 0+2\cdot 0}{4−5\cdot 0+7\cdot 0}=\frac{0}{4}=0. \nonumber \]
Portanto,\(f\) tem uma assíntota horizontal de\(y=0\) como mostrado no gráfico a seguir.
c. Dividindo o numerador e o denominador por\(x\), temos
\[\displaystyle \lim_{x→±∞}\frac{3x^2+4x}{x+2}=\lim_{x→±∞}\frac{3x+4}{1+2/x}. \nonumber \]
À medida que\(x→±∞\) o denominador se aproxima\(1\). À medida que\(x→∞\) o numerador se aproxima\(+∞\). À medida que\(x→−∞\) o numerador se aproxima\(−∞\). Portanto\(\displaystyle \lim_{x→∞}f(x)=∞\), considerando que,\(\displaystyle \lim_{x→−∞}f(x)=−∞\) conforme mostrado na figura a seguir.
Avalie\(\displaystyle \lim_{x→±∞}\frac{3x^2+2x−1}{5x^2−4x+7}\) e use esses limites para determinar o comportamento final do\(f(x)=\dfrac{3x^2+2x−1}{5x^2−4x+7}\).
- Dica
-
Divida o numerador e o denominador por\(x^2\).
- Responda
-
\(\frac{3}{5}\)
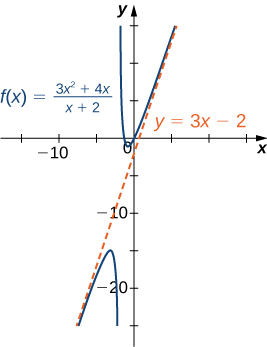
Antes de continuar, considere o gráfico\(f(x)=\dfrac{3x^2+4x}{x+2}\) mostrado na Figura\(\PageIndex{16}\). Como\(x→∞\) e\(x→−∞\), o gráfico de\(f\) parece quase linear. Embora certamente não\(f\) seja uma função linear, agora investigamos por que o gráfico de\(f\) parece estar se aproximando de uma função linear. Primeiro, usando a divisão longa de polinômios, podemos escrever
\[f(x)=\frac{3x^2+4x}{x+2}=3x−2+\frac{4}{x+2}. \nonumber \]
Pois\(\dfrac{4}{x+2}→0\), ao\(x→±∞,\) concluirmos que
\[ \lim_{x→±∞}(f(x)−(3x−2))=\lim_{x→±∞}\frac{4}{x+2}=0. \nonumber \]
Portanto, o gráfico de\(f\) se aproxima da linha\(y=3x−2\) como\(x→±∞\). Essa linha é conhecida como assíntota oblíqua para\(f\) (Figura\(\PageIndex{17}\)).
Podemos resumir os resultados do Example\(\PageIndex{5}\) para fazer a seguinte conclusão sobre o comportamento final de funções racionais. Considere uma função racional
\[f(x)=\frac{p(x)}{q(x)}=\frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0},\nonumber \]
onde\(a_n≠0\) e\(b_m≠0.\)
- Se o grau do numerador for o mesmo que o grau do denominador\((n=m),\), então\(f\) tem uma assíntota horizontal de\(y=a_n/b_m\) como\(x→±∞.\)
- Se o grau do numerador for menor que o grau do denominador\((n<m),\), então\(f\) tem uma assíntota horizontal de\(y=0\) como\(x→±∞.\)
- Se o grau do numerador for maior que o grau do denominador\((n>m),\), então\(f\) não tem uma assíntota horizontal. Os limites no infinito são infinitos positivos ou negativos, dependendo dos sinais dos termos principais. Além disso, usando divisão longa, a função pode ser reescrita\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x)}, \nonumber \] quando o grau de\(r(x)\) é menor que o grau de\(q(x)\). Como resultado,\(\displaystyle \lim_{x→±∞}r(x)/q(x)=0\). Portanto, os valores se\([f(x)−g(x)]\) aproximam de zero como\(x→±∞\). Se o grau de\(p(x)\) for exatamente um a mais do que o grau de\(q(x)\) (ou seja,\(n=m+1\)), a função\(g(x)\) é linear. Nesse caso,\(g(x)\) chamamos de assíntota oblíqua.
Agora, vamos considerar o comportamento final das funções que envolvem um radical.
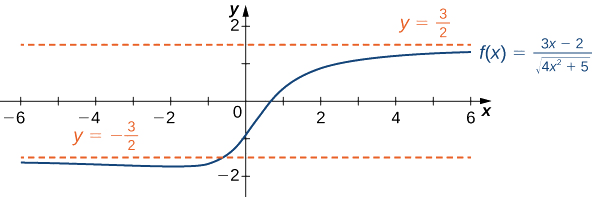
Encontre os limites como\(x→∞\) e\(x→−∞\) para\(f(x)=\dfrac{3x−2}{\sqrt{4x^2+5}}\) e descreva o comportamento final de\(f\).
Solução
Vamos usar a mesma estratégia que usamos para funções racionais: dividir o numerador e o denominador por uma potência de\(x\). Para determinar a potência apropriada de\(x\), considere a expressão\(\sqrt{4x^2+5}\) no denominador. Desde
\[\sqrt{4x^2+5}≈\sqrt{4x^2}=2|x| \nonumber \]
para grandes valores de\(x\) efeito\(x\) aparece apenas na primeira potência no denominador. Portanto, dividimos o numerador e o denominador por\(|x|\). Em seguida, usando o fato de que\(|x|=x\)\(x>0, |x|=−x\) para\(x<0\),\(|x|=\sqrt{x^2}\) para e para todos\(x\), calculamos os limites da seguinte forma:
\ [\ begin {align*}\ lim_ {x→∞}\ frac {3x−2} {\ sqrt {4x^2+5}} &=\ lim_ {x→∞}\ frac {(1/|x|) (3x−2)} {(1/|x|)\ sqrt {4x^2+5}}\\ [4pt]
&=\ lim_ {x→∞}\ frac {(1/x) (3x−2)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→∞}\ frac {3−2/x} {\ sqrt {4+5/x^2}} =\ frac {3} {\ sqrt {4}} =\ frac {3} {\ sqrt {4}} =\ frac {3} {2}\ end {align*}\]
\ [\ begin {align*}\ lim_ {x→−∞}\ frac {3x−2} {\ sqrt {4x^2+5}} &=\ lim_ {x→−∞}\ frac {(1/|x|) (3x−2)} {(1/|x|)\ sqrt {4x^2+5}}\\ [4pt]
&=\ lim_ {x→−∞}\ frac {(−1/x) (3x−2)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→−∞}\ frac {−3+2/x} {\ sqrt {4+5/x^2}} =\ frac {−3}\ sqrt {4}} =\ frac {−3} {2}. \ end {align*}\]
Portanto,\(f(x)\) se aproxima da assíntota horizontal\(y=\frac{3}{2}\) como\(x→∞\) e da assíntota horizontal\(y=−\frac{3}{2}\)\(x→−∞\) conforme mostrado no gráfico a seguir.
Avalie\(\displaystyle \lim_{x→∞}\frac{\sqrt{3x^2+4}}{x+6}\).
- Dica
-
Divida o numerador e o denominador por\(x\).
- Responda
-
\(\sqrt{3}\)
Determinando o comportamento final para funções transcendentais
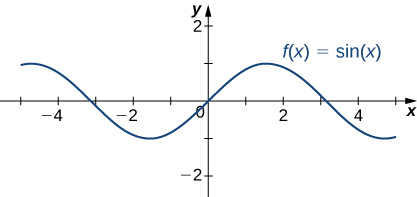
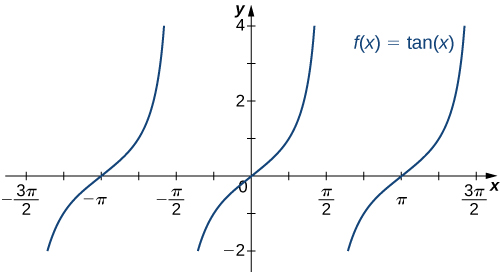
As seis funções trigonométricas básicas são periódicas e não se aproximam de um limite finito, pois,\(x→±∞.\) por exemplo,\(\sin x\) oscila entre 1 e -1 (Figura\(\PageIndex{19}\)). A função tangente\(x\) tem um número infinito de assíntotas verticais como\(x→±∞\); portanto, ela não se aproxima de um limite finito nem se aproxima\(±∞\)\(x→±∞\) conforme mostrado na Figura\(\PageIndex{20}\).
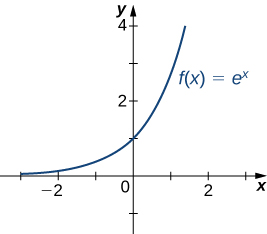
Lembre-se de que, para qualquer base,\(b>0,\; b≠1,\) a função\(y=b^x\) é uma função exponencial com domínio\((−∞,∞)\) e alcance\((0,∞)\). \(b>1,\;y=b^x\)Está aumentando\((−∞,∞)\). If\(0<b<1, \; y=b^x\) está diminuindo em\((−∞,∞).\) Para a função exponencial natural\(f(x)=e^x, \; e≈2.718>1\). Portanto,\(f(x)=e^x\) está aumentando\((−∞,∞)\) e o alcance é\((0,∞)\). A função exponencial\(f(x)=e^x\) se\(∞\) aproxima\(x→∞\) e se aproxima\(0\)\(x→−∞\) conforme mostrado na Tabela\(\PageIndex{4}\) e na Figura\(\PageIndex{21}\).
| \(x\) | −5 | −2 | 0 | 2 | 5 |
|---|---|---|---|---|---|
| \(e^x\) | 0,00674 | 0,135 | 1 | 7.389 | 148.413 |
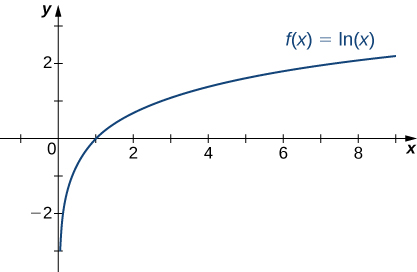
Lembre-se de que a função logarítmica natural\(f(x)=\ln(x)\) é o inverso da função exponencial natural\(y=e^x\). Portanto, o domínio de\(f(x)=\ln(x)\) é\((0,∞)\) e o intervalo é\((−∞,∞)\). O gráfico de\(f(x)=\ln(x)\) é o reflexo do gráfico de\(y=e^x\) cerca da linha\(y=x\). Portanto,\(\ln(x)→−∞\) como\(x→0^+\) e\(\ln(x)→∞\)\(x→∞\) conforme mostrado na Figura\(\PageIndex{22}\) e na Tabela\(\PageIndex{5}\).
| \(x\) | 0,01 | 0.1 | 1 | 10 | 100 |
|---|---|---|---|---|---|
| \(\ln(x)\) | −4,605 | −2,303 | 0 | 2.303 | 4.605 |
Encontre os limites como\(x→∞\) e\(x→−∞\) para\(f(x)=\dfrac{2+3e^x}{7−5e^x}\) e descreva o comportamento final de\(f.\)
Solução
Para encontrar o limite,\(x→∞,\) divida o numerador e o denominador por\(e^x\):
\[ \begin{align*} \lim_{x→∞}f(x) &= \lim_{x→∞}\frac{2+3e^x}{7−5e^x} \\[4pt] &=\lim_{x→∞}\frac{(2/e^x)+3}{(7/e^x)−5.} \end{align*}\]
Conforme mostrado na Figura\(\PageIndex{21}\),\(e^x→∞\) como\(x→∞\). Portanto,
\(\displaystyle \lim_{x→∞}\frac{2}{e^x}=0=\lim_{x→∞}\frac{7}{e^x}\).
Concluímos que\(\displaystyle \lim_{x→∞}f(x)=−\frac{3}{5}\), e o gráfico de\(f\) se aproxima da assíntota horizontal\(y=−\frac{3}{5}\) como\(x→∞.\) Para encontrar o limite como\(x→−∞\), use o fato de que\(e^x→0\),\(x→−∞\) para concluir que\(\displaystyle \lim_{x→-∞}f(x)=\frac{2}{7}\), e, portanto, o gráfico de\(f(x)\) se aproxima da assíntota horizontal \(y=\frac{2}{7}\)como\(x→−∞\).
Encontre os limites como\(x→∞\) e\(x→−∞\) para\(f(x)=\dfrac{3e^x−4}{5e^x+2}\).
- Dica
-
\(\displaystyle \lim_{x→∞}e^x=∞\)e\(\displaystyle \lim_{x→-∞}e^x=0.\)
- Responda
-
\(\displaystyle \lim_{x→∞}f(x)=\frac{3}{5}, \quad\lim_{x→−∞}f(x)=−2\)
Diretrizes para desenhar o gráfico de uma função
Agora temos ferramentas analíticas suficientes para desenhar gráficos de uma grande variedade de funções algébricas e transcendentais. Antes de mostrar como representar graficamente funções específicas, vamos analisar uma estratégia geral a ser usada ao representar graficamente qualquer função.
Dada uma função\(f\), use as etapas a seguir para esboçar um gráfico de\(f\):
- Determine o domínio da função.
- Localize as\(y\) interceptações\(x\) - e -.
- Avalie\(\displaystyle \lim_{x→∞}f(x)\) e\(\displaystyle \lim_{x→−∞}f(x)\) determine o comportamento final. Se um desses limites for um número finito\(L\), então\(y=L\) é uma assíntota horizontal. Se um desses limites for\(∞\) ou\(−∞\), determine se\(f\) tem uma assíntota oblíqua. Se\(f\) é uma função racional tal que\(f(x)=\dfrac{p(x)}{q(x)}\), onde o grau do numerador é maior que o grau do denominador, então\(f\) pode ser escrito como\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x),} \nonumber \] onde o grau de\(r(x)\) é menor que o grau de\(q(x)\). Os valores de\(f(x)\) se aproximam dos valores de\(g(x)\) as\(x→±∞\). Se\(g(x)\) for uma função linear, é conhecida como assíntota oblíqua.
- Determine se\(f\) tem alguma assíntota vertical.
- Calcule\(f′.\) Encontre todos os pontos críticos e determine os intervalos onde\(f\) está aumentando e onde\(f\) está diminuindo. Determine se\(f\) tem algum extremo local.
- Calcule\(f''.\) Determine os intervalos onde\(f\) é côncavo para cima e onde\(f\) é côncavo para baixo. Use essas informações para determinar se\(f\) tem algum ponto de inflexão. A segunda derivada também pode ser usada como um meio alternativo para determinar ou verificar se\(f\) tem um extremo local em um ponto crítico.
Agora, vamos usar essa estratégia para representar graficamente várias funções diferentes. Começamos representando graficamente uma função polinomial.
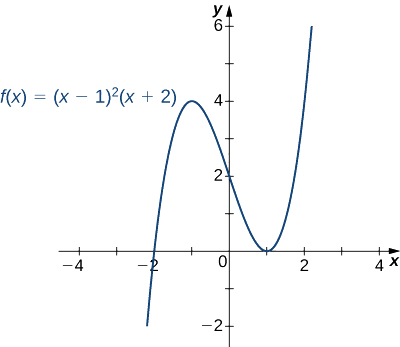
Esboce um gráfico de\(f(x)=(x−1)^2(x+2).\)
Solução
Etapa 1: Como\(f\) é um polinômio, o domínio é o conjunto de todos os números reais.
Etapa 2: Quando,\(x=0,\; f(x)=2.\) portanto, o\(y\) -intercept é\((0,2)\). Para encontrar os\(x\) interceptos -, precisamos resolver a equação\((x−1)^2(x+2)=0\), que nos dá os\(x\) interceptos\((1,0)\) -e\((−2,0)\)
Etapa 3: Precisamos avaliar o comportamento final\(f.\) de As\(x→∞, \;(x−1)^2→∞\)\((x+2)→∞\) e. Portanto,\(\displaystyle \lim_{x→∞}f(x)=∞\).
Como\(x→−∞, \;(x−1)^2→∞\)\((x+2)→−∞\) e. Portanto,\(\displaystyle \lim_{x→-∞}f(x)=−∞\).
Para obter ainda mais informações sobre o comportamento final do\(f\), podemos multiplicar os fatores de\(f\). Ao fazer isso, vemos que
\[f(x)=(x−1)^2(x+2)=x^3−3x+2. \nonumber \]
Como o termo principal de\(f\) é\(x^3\), concluímos que\(f\) se comporta\(y=x^3\) como\(x→±∞.\)
Etapa 4: Como\(f\) é uma função polinomial, ela não tem assíntotas verticais.
Etapa 5: A primeira derivada de\(f\) é
\[f′(x)=3x^2−3. \nonumber \]
Portanto,\(f\) tem dois pontos críticos:\(x=1,−1.\) Divida o intervalo\((−∞,∞)\) em três intervalos menores:\((−∞,−1), \;(−1,1)\),\((1,∞)\) e. Em seguida, escolha os pontos de teste e\(x=−2, x=0\),\(x=2\) a partir desses intervalos, avalie o sinal de\(f′(x)\) em cada um desses pontos de teste, conforme mostrado na tabela a seguir.
| Intervalo | Ponto de teste | Sinal de derivada\(f'(x)=3x^2−3=3(x−1)(x+1)\) | Conclusão |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">\((+)(−)(−)=+\) | \(f\)está aumentando |
| \((−1,1)\) | \(x=0\) | \ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">\((+)(−)(+)=−\) | \(f\)diminuindo |
| \((1,∞)\) | \(x=2\) | \ (f' (x) =3x^2−3=3 (x−1) (x+1)\)” style="text-align:center; ">\((+)(+)(+)=+\) | \(f\)está aumentando |
Na tabela, vemos que\(f\) tem um máximo local em\(x=−1\) e um mínimo local em\(x=1\). \(f(x)\)Avaliando esses dois pontos, descobrimos que o valor máximo local é\(f(−1)=4\) e o valor mínimo local é\(f(1)=0.\)
Etapa 6: A segunda derivada de\(f\) é
\[f''(x)=6x. \nonumber \]
A segunda derivada é zero em\(x=0.\) Portanto, para determinar a concavidade de\(f\), divida o intervalo\((−∞,∞)\) em intervalos menores\((−∞,0)\) e\((0,∞)\), e escolha pontos de teste\(x=−1\) e determine\(x=1\) a concavidade de\(f\) em cada um desses intervalos menores conforme mostrado na tabela a seguir.
| Intervalo | Ponto de teste | Sinal de\(f''(x)=6x\) | Conclusão |
|---|---|---|---|
| \((−∞,0)\) | \(x=−1\) | \ (f "(x) =6x\)” style="alinhamento do texto: centro; ">\(−\) | \(f\)é côncavo para baixo. |
| \((0,∞)\) | \(x=1\) | \ (f "(x) =6x\)” style="alinhamento do texto: centro; ">\(+\) | \(f\)é côncavo para cima. |
Observamos que as informações na tabela anterior confirmam o fato, encontrado na etapa\(5\), de que f tem um máximo local em\(x=−1\) e um mínimo local em\(x=1\). Além disso, as informações encontradas na etapa\(5\) — ou seja,\(f\) têm um máximo local em\(x=−1\) e um mínimo local\(f′(x)=0\) em\(x=1\) e nesses pontos — combinado com o fato de que\(f''\) as alterações assinam somente em\(x=0\) confirma os resultados encontrados\(6\) na etapa do concavidade de\(f\).
Combinando essas informações, chegamos ao gráfico\(f(x)=(x−1)^2(x+2)\) mostrado no gráfico a seguir.
Esboce um gráfico de\(f(x)=(x−1)^3(x+2).\)
- Dica
-
\(f\)é um polinômio de quarto grau.
- Responda
-
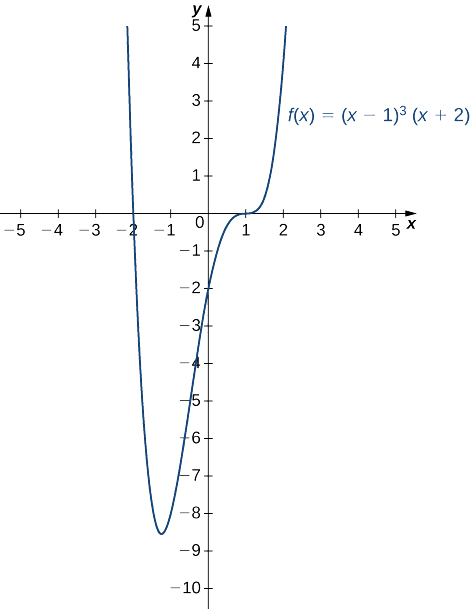
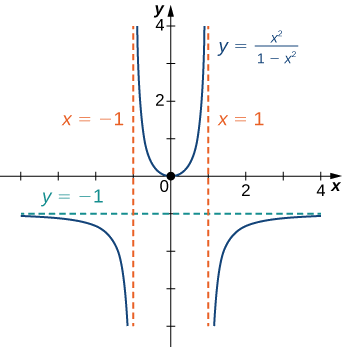
Esboce o gráfico de\(f(x)=\dfrac{x^2}{1−x^2}\).
Solução
Etapa 1: A função\(f\) é definida desde que o denominador não seja zero. Portanto, o domínio é o conjunto de todos os números reais\(x\), exceto\(x=±1.\)
Etapa 2: Encontre as interceptações. Se\(x=0,\) então\(f(x)=0\), o mesmo\(0\) acontece com uma interceptação. Se\(y=0\), então\(\dfrac{x^2}{1−x^2}=0,\) o que implica\(x=0\). Portanto,\((0,0)\) é a única interceptação.
Etapa 3: Avalie os limites no infinito. Como\(f\) é uma função racional, divida o numerador e o denominador pela maior potência no denominador:\(x^2\) .Obtemos
\(\displaystyle \lim_{x→±∞}\frac{x^2}{1−x^2}=\lim_{x→±∞}\frac{1}{\frac{1}{x^2}−1}=−1.\)
Portanto,\(f\) tem uma assíntota horizontal de\(y=−1\) como\(x→∞\) e\(x→−∞.\)
Etapa 4: Para determinar se\(f\) tem alguma assíntota vertical, primeiro verifique se o denominador tem zeros. Descobrimos que o denominador é zero quando\(x=±1\). Para determinar se as linhas\(x=1\) ou\(x=−1\) são assíntotas verticais de\(f\),\(\displaystyle \lim_{x→1}f(x)\) avalie\(\displaystyle \lim_{x→−1}f(x)\) e. Observando cada limite unilateral,\(x→1,\) vemos que
\(\displaystyle \lim_{x→1^+}\frac{x^2}{1−x^2}=−∞\)e\(\displaystyle \lim_{x→1^−}\frac{x^2}{1−x^2}=∞.\)
Além disso, observando cada limite unilateral à medida que\(x→−1,\) descobrimos que
\(\displaystyle \lim_{x→−1^+}\frac{x^2}{1−x^2}=∞\)e\(\displaystyle \lim_{x→−1^−}\frac{x^2}{1−x^2}=−∞.\)
Etapa 5: Calcule a primeira derivada:
\(f′(x)=\dfrac{(1−x^2)(2x)−x^2(−2x)}{\Big(1−x^2\Big)^2}=\dfrac{2x}{\Big(1−x^2\Big)^2}\).
Os pontos críticos ocorrem em pontos\(x\) onde\(f′(x)=0\) ou\(f′(x)\) estão indefinidos. Vemos isso\(f′(x)=0\) quando\(x=0.\) a derivada não\(f′\) é indefinida em nenhum ponto do domínio de\(f\). No entanto, não\(x=±1\) estão no domínio de\(f\). Portanto, para determinar onde\(f\) está aumentando e onde\(f\) está diminuindo, divida o intervalo\((−∞,∞)\) em quatro intervalos menores:\((−∞,−1), (−1,0), (0,1),\) e\((1,∞)\) escolha um ponto de teste em cada intervalo para determinar o sinal de\(f′(x)\) em cada um desses intervalos. Os valores\(x=−2,\; x=−\frac{1}{2}, \;x=\frac{1}{2}\) e\(x=2\) são boas escolhas para pontos de teste, conforme mostrado na tabela a seguir.
| Intervalo | Ponto de teste | Sinal de\(f′(x)=\frac{2x}{(1−x^2)^2}\) | Conclusão |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f′f (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(−/+=−\) | \(f\)está diminuindo. |
| \((−1,0)\) | \(x=−1/2\) | \ (f′f (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(−/+=−\) | \(f\)está diminuindo. |
| \((0,1)\) | \(x=1/2\) | \ (f′f (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(+/+=+\) | \(f\)está aumentando. |
| \((1,∞)\) | \(x=2\) | \ (f′f (x) =\ frac {2x} {(1−x^2) ^2}\)” style="text-align:center; ">\(+/+=+\) | \(f\)está aumentando. |
A partir dessa análise, concluímos que\(f\) tem um mínimo local em\(x=0\), mas nenhum máximo local.
Etapa 6: Calcule a segunda derivada:
\ [\ begin {align*} f "(x) &=\ frac {(1−x^2) ^2 (2) −2x (2 (1−x^2) (−2x)))} {(1−x^2) ^4}\\ [4pt]
&=\ frac {(1−x^2) [2 (1−x^2) +8x^2]} {\ Grande (1−x^2\ Grande) ^4}\\ [4pt]
&=\ frac {2 (1−x^2) +8x^2} {\ Grande (1−x^2\ Grande) ^3}\\ [4pt]
&=\ frac {6x^2+2} {\ Grande (1−x^2\ Grande) ^3}. \ end {align*}\]
Para determinar os intervalos onde\(f\) é côncavo para cima e onde\(f\) é côncavo para baixo, primeiro precisamos encontrar todos os pontos\(x\) onde\(f''(x)=0\) ou\(f''(x)\) estão indefinidos. Já que o numerador\(6x^2+2≠0\) de qualquer\(x, f''(x)\) um nunca é zero. Além disso, não\(f''\) é indefinido para nenhum\(x\) no domínio de\(f\). No entanto, conforme discutido anteriormente, não\(x=±1\) estão no domínio de\(f\). Portanto, para determinar a concavidade de\(f\), dividimos o intervalo\((−∞,∞)\) em três intervalos\((−∞,−1), \, (−1,1)\) menores e\((1,∞)\) escolhemos um ponto de teste em cada um desses intervalos para avaliar o sinal de\(f''(x)\). Os valores\(x=−2, \;x=0\) e\(x=2\) são possíveis pontos de teste, conforme mostrado na tabela a seguir.
| Intervalo | Ponto de teste | Sinal de\(f''(x)=\frac{6x^2+2}{(1−x^2)^3}\) | Conclusão |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">\(+/−=−\) | \(f\)é côncavo para baixo. |
| \((−1,1)\) | \(x=0\) | \ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">\(+/+=+\) | \(f\)é côncavo para cima |
| \((1,∞)\) | \(x=2\) | \ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)” style="text-align:center; ">\(+/−=−\) | \(f\)é côncavo para baixo. |
Combinando todas essas informações, chegamos ao gráfico\(f\) mostrado abaixo. Observe que, embora\(f\) mude a concavidade em\(x=−1\) e\(x=1\), não há pontos de inflexão em nenhum desses lugares porque não\(f\) é contínuo em\(x=−1\) ou\(x=1.\)
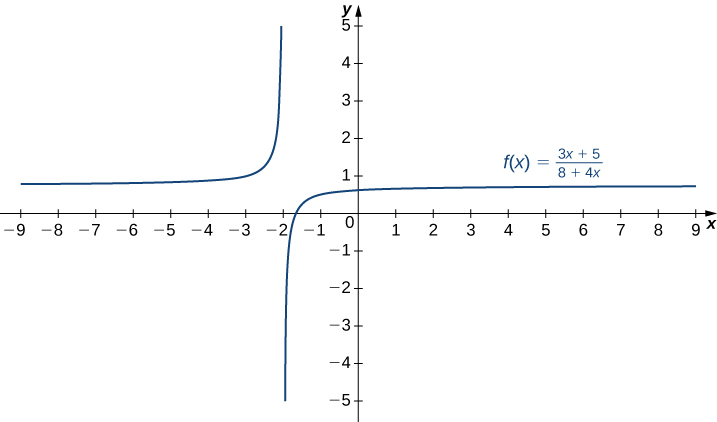
Esboce um gráfico de\(f(x)=\dfrac{3x+5}{8+4x}.\)
- Dica
-
Uma linha\(y=L\) é uma assíntota horizontal de\(f\) se o limite como\(x→∞\) ou o limite a partir\(x→−∞\) de\(f(x)\) é\(L\). Uma linha\(x=a\) é uma assíntota vertical se pelo menos um dos limites unilaterais de\(f\) como\(x→a\) é\(∞\) ou\(−∞.\)
- Responda
-
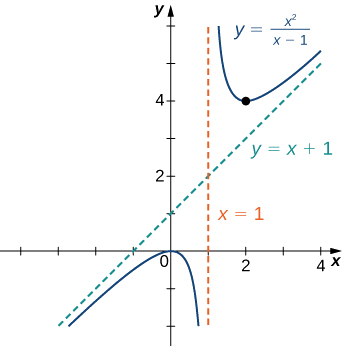
Esboce o gráfico de\(f(x)=\dfrac{x^2}{x−1}\)
Solução
Etapa 1: O domínio de\(f\) é o conjunto de todos os números reais\(x\), exceto\(x=1.\)
Etapa 2: Encontre as interceptações. Podemos ver que, quando\(x=0, \,f(x)=0,\) sim,\((0,0)\) é a única interceptação.
Etapa 3: Avalie os limites no infinito. Como o grau do numerador é um a mais que o grau do denominador,\(f\) deve ter uma assíntota oblíqua. Para encontrar a assíntota oblíqua, use a divisão longa de polinômios para escrever
\(f(x)=\dfrac{x^2}{x−1}=x+1+\dfrac{1}{x−1}\).
Uma vez que\(\dfrac{1}{x−1}→0\) tão\(x→±∞, f(x)\) se aproxima da linha\(y=x+1\) quanto\(x→±∞\). A linha\(y=x+1\) é uma assíntota oblíqua para\(f\).
Etapa 4: Para verificar se há assíntotas verticais, veja onde o denominador é zero. Aqui, o denominador é zero em\(x=1.\) Olhando para os dois limites unilaterais conforme\(x→1,\) encontramos
\(\displaystyle \lim_{x→1^+}\frac{x^2}{x−1}=∞\)e\(\displaystyle \lim_{x→1^−}\frac{x^2}{x−1}=−∞.\)
Portanto,\(x=1\) é uma assíntota vertical, e determinamos o comportamento da\(f\) medida que\(x\) se aproxima\(1\) da direita e da esquerda.
Etapa 5: Calcule a primeira derivada:
\(f′(x)=\dfrac{(x−1)(2x)−x^2(1)}{(x−1)^2}=\dfrac{x^2−2x}{(x−1)^2}.\)
Nós temos\(f′(x)=0\) quando\(x^2−2x=x(x−2)=0\). Portanto,\(x=0\) e\(x=2\) são pontos críticos. Como\(f\) é indefinido em\(x=1\), precisamos dividir o intervalo\((−∞,∞)\) em intervalos menores\((−∞,0), (0,1), (1,2),\) e\((2,∞)\) escolher um ponto de teste de cada intervalo para avaliar o sinal de\(f′(x)\) em cada um desses intervalos menores. Por exemplo\(x=−1, x=\frac{1}{2}, x=\frac{3}{2}\), sejam e\(x=3\) sejam os pontos de teste, conforme mostrado na tabela a seguir.
| Intervalo | Ponto de teste | Sinal de\(f'(x)=\dfrac{x^2−2x}{(x−1)^2}\) | Conclusão |
|---|---|---|---|
| \((−∞,0)\) | \(x=−1\) | \ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” data-valign="top"> (−) (−) /+=+ | \(f\)está aumentando. |
| \((0,1)\) | \(x=1/2\) | \ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” data-valign="top"> (+) (−) /+=− | \(f\)está diminuindo. |
| \((1,2)\) | \(x=3/2\) | \ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” data-valign="top"> (+) (−) /+=− | \(f\)está diminuindo. |
| \((2,∞)\) | \(x=3\) | \ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)” data-valign="top"> (+) (+) /+=+ | \(f\)está aumentando. |
Nesta tabela, vemos que\(f\) tem um máximo local em\(x=0\) e um mínimo local em\(x=2\). O valor de\(f\) no máximo local é\(f(0)=0\) e o valor de\(f\) no mínimo local é\(f(2)=4\). Portanto,\((0,0)\) e\((2,4)\) são pontos importantes no gráfico.
Etapa 6. Calcule a segunda derivada:
\ [\ begin {align*} f "(x) &=\ frac {(x−1) ^2 (2x−2) −2 (x−1) (x^2−2x)} {(x−1) ^4}\\ [4pt]
&=\ frac {2 (x−1) [(x−1) ^2− (x^2−2x)]} {(x−1) ^4}\\ [4pt]
&=\ frac {2 [x^2-2x+1−x^2+2x]} {(x−1) ^3}\ [4pt]
&=\ frac {2} {(x−1) ^3}. \ end {align*}\]
Vemos que isso nunca\(f''(x)\) é zero ou indefinido\(x\) no domínio de\(f\). Como\(f\) é indefinido em\(x=1\), para verificar a concavidade\((1,∞)\), basta\((−∞,∞)\) dividir o intervalo em dois intervalos menores\((−∞,1)\) e escolher um ponto de teste de cada intervalo para avaliar o sinal de\(f''(x)\) em cada um desses intervalos. Os valores\(x=0\) e\(x=2\) são possíveis pontos de teste, conforme mostrado na tabela a seguir.
| Intervalo | Ponto de teste | Sinal de\(f''(x)=\dfrac{2}{(x−1)^3}\) | Conclusão |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f "(x) =\ dfrac {2} {(x−1) ^3}\)” style="text-align:center; ">\(+/−=−\) | \(f\)é côncavo para baixo. |
| \((1,∞)\) | \(x=2\) | \ (f "(x) =\ dfrac {2} {(x−1) ^3}\)” style="text-align:center; ">\(+/+=+\) | \(f\)é côncavo para cima |
A partir das informações coletadas, chegamos ao seguinte gráfico para\(f.\)
Encontre a assíntota oblíqua para\(f(x)=\dfrac{3x^3−2x+1}{2x^2−4}\).
- Dica
-
Use divisão longa de polinômios.
- Responda
-
\(y=\frac{3}{2}x\)
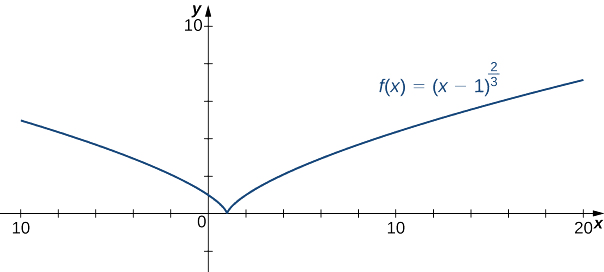
Esboce um gráfico de\(f(x)=(x−1)^{2/3}\)
Solução
Etapa 1: Como a função de raiz cúbica é definida para todos os números reais\(x\) e\((x−1)^{2/3}=(\sqrt[3]{x−1})^2\), o domínio de\(f\) são todos números reais.
Etapa 2: Para encontrar o\(y\) -intercept, avalie\(f(0)\). Uma vez que\(f(0)=1,\) o\(y\) intercepto -é\((0,1)\). Para encontrar o\(x\) intercepto -, resolva\((x−1)^{2/3}=0\). A solução dessa equação é\(x=1\), então o\(x\) intercepto -é\((1,0).\)
Etapa 3: Como\(\displaystyle \lim_{x→±∞}(x−1)^{2/3}=∞,\) a função continua a crescer sem limites como\(x→∞\) e\(x→−∞.\)
Etapa 4: A função não tem assíntotas verticais.
Etapa 5: Para determinar onde\(f\) está aumentando ou diminuindo, calcule\(f′.\) Nós encontramos
\[f′(x)=\frac{2}{3}(x−1)^{−1/3}=\frac{2}{3(x−1)^{1/3}} \nonumber \]
Essa função não é zero em nenhum lugar, mas é indefinida quando\(x=1.\) Portanto, o único ponto crítico é\(x=1.\) Divida o intervalo\((−∞,∞)\) em intervalos menores\((−∞,1)\) e\((1,∞)\), e escolha pontos de teste em cada um desses intervalos para determinar o sinal de\(f′(x)\) em cada um deles intervalos menores. Seja\(x=0\) e\(x=2\) seja os pontos de teste, conforme mostrado na tabela a seguir.
| Intervalo | Ponto de teste | Sinal de\(f′(x)=\frac{2}{3(x−1)^{1/3}}\) | Conclusão |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f′f (x) =\ frac {2} {3 (x−1) ^ {1/3}}\)” style="text-align:center; ">\(+/−=−\) | \(f\)está diminuindo |
| \((1,∞)\) | \(x=2\) | \ (f′f (x) =\ frac {2} {3 (x−1) ^ {1/3}}\)” style="text-align:center; ">\(+/+=+\) | \(f\)está aumentando |
Concluímos que\(f\) tem um mínimo local em\(x=1\). Avaliando\(f\) em\(x=1\), descobrimos que o valor de\(f\) no mínimo local é zero. Observe que\(f′(1)\) é indefinido, portanto, para determinar o comportamento da função neste ponto crítico, precisamos examinar.\(\displaystyle \lim_{x→1}f′(x).\) Observando os limites unilaterais, temos
\[\lim_{x→1^+}\frac{2}{3(x−1)^{1/3}}=∞\text{ and } \lim_{x→1^−}\frac{2}{3(x−1)^{1/3}}=−∞.\nonumber \]
Portanto,\(f\) tem uma cúspide em\(x=1.\)
Etapa 6: Para determinar a concavidade, calculamos a segunda derivada de\(f:\)
\[f''(x)=−\dfrac{2}{9}(x−1)^{−4/3}=\dfrac{−2}{9(x−1)^{4/3}}. \nonumber \]
Descobrimos que isso\(f''(x)\) é definido para todos\(x\), mas é indefinido quando\(x=1\). Portanto, divida o intervalo\((−∞,∞)\) em intervalos menores\((−∞,1)\) e\((1,∞)\) escolha pontos de teste para avaliar o sinal de\(f''(x)\) em cada um desses intervalos. Como fizemos anteriormente, vamos\(x=0\) testar pontos conforme mostrado na tabela a seguir.\(x=2\)
| Intervalo | Ponto de teste | Sinal de\(f''(x)=\dfrac{−2}{9(x−1)^{4/3}}\) | Conclusão |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f "(x) =\ dfrac {−2} {9 (x−1) ^ {4/3}}\)” style="text-align:center; ">\(−/+=−\) | \(f\)é côncavo para baixo |
| \((1,∞)\) | \(x=2\) | \ (f "(x) =\ dfrac {−2} {9 (x−1) ^ {4/3}}\)” style="text-align:center; ">\(−/+=−\) | \(f\)é côncavo para baixo |
A partir desta tabela, concluímos que\(f\) é côncavo em todos os lugares. Combinando todas essas informações, chegamos ao gráfico a seguir para\(f\).
Considere a função\(f(x)=5−x^{2/3}\). Determine o ponto no gráfico em que uma cúspide está localizada. Determine o comportamento final do\(f\).
- Dica
-
Uma função\(f\) tem uma cúspide em um ponto,\(a\) se\(f(a)\) existir,\(f'(a)\) é indefinida, um dos limites unilaterais a partir\(x→a\) de\(f'(x)\) é\(+∞\) e o outro limite unilateral é\(−∞.\)
- Responda
-
A função\(f\) tem uma cúspide em\((0,5)\), uma vez que\(\displaystyle \lim_{x→0^−}f′(x)=∞\)\(\displaystyle \lim_{x→0^+}f′(x)=−∞\) e. Para o comportamento final,\(\displaystyle \lim_{x→±∞}f(x)=−∞.\)
Conceitos-chave
- O limite de\(f(x)\) é\(L\) como\(x→∞\) (ou como\(x→−∞)\) se os valores se\(f(x)\) tornassem arbitrariamente próximos ao que\(L\)\(x\) se tornassem suficientemente grandes).
- O limite de\(f(x)\) é\(∞\) como\(x→∞\) se\(f(x)\) tornasse arbitrariamente grande à medida que\(x\) se tornasse suficientemente grande. O limite de\(f(x)\) é\(−∞\) como\(x→∞\) se\(f(x)<0\) e se\(|f(x)|\) torna arbitrariamente grande à medida que\(x\) se torna suficientemente grande. Podemos definir o limite de\(f(x)\) como\(x\) abordagens\(−∞\) semelhantes.
- Para uma função polinomial\(p(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0,\) em que\(a_n≠0\), o comportamento final é determinado pelo termo principal\(a_nx^n\). Se se\(n≠0, p(x)\)\(∞\) aproximar ou\(−∞\) em cada extremidade.
- Para uma função racional,\(f(x)=\dfrac{p(x)}{q(x),}\) o comportamento final é determinado pela relação entre o grau de\(p\) e o grau de\(q\). Se o grau de\(p\) for menor que o grau de\(q\), a linha\(y=0\) é uma assíntota horizontal para\(f\). Se o grau de\(p\) for igual ao grau de\(q\), então a linha\(y=\dfrac{a_n}{b_n}\) é uma assíntota horizontal, onde\(a_n\) e\(b_n\) são os coeficientes principais de\(p\) e\(q\), respectivamente. Se o grau de\(p\) for maior que o grau de\(q\), então\(f\) se aproxima\(∞\) ou\(−∞\) em cada extremidade.
Glossário
- comportamento final
- o comportamento de uma função como\(x→∞\) e\(x→−∞\)
- assíntota horizontal
- se\(\displaystyle \lim_{x→∞}f(x)=L\) ou\(\displaystyle \lim_{x→−∞}f(x)=L\), então\(y=L\) é uma assíntota horizontal de\(f\)
- limite infinito no infinito
- uma função que se torna arbitrariamente grande à medida que\(x\) se torna grande
- limite no infinito
- uma função que se aproxima de um valor limite\(L\) à medida que\(x\) se torna grande
- assíntota oblíqua
- a linha\(y=mx+b\) se\(f(x)\) aproxima dela como\(x→∞\) ou\( x→−∞\)


