4.5E: Exercícios para a Seção 4.5

Last updated
Save as PDF

Page ID: 188257

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) Se$c$ for um ponto crítico de$f(x)$, quando não há máximo ou mínimo local em$c$? Explique.

2) Para a função$y=x^3$, é$x=0$ tanto um ponto de inflexão quanto um máximo/mínimo local?

Responda: Não é um máximo/mínimo local porque$f'$ não altera o sinal

3) Para a função$y=x^3$, é$x=0$ um ponto de inflexão?

4) É possível que um ponto$c$ seja tanto um ponto de inflexão quanto um extremo local de uma função duas vezes diferenciável?

Responda: Não

5) Por que você precisa de continuidade para o primeiro teste derivado? Invente um exemplo.

6) Explique se uma função côncava para baixo precisa ser cruzada$y=0$ para algum valor de$x$.

Resposta: Falso; por exemplo,$y=\sqrt{x}$.

7) Explique se um polinômio de grau$2$ pode ter um ponto de inflexão.

Nos exercícios 8 a 12, analise os gráficos de e, em seguida$f'$, liste todos os intervalos em que$f$ está aumentando ou diminuindo.

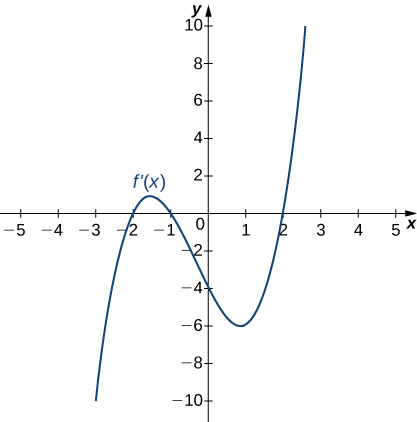
$A função f' (x) é representada graficamente. A função começa com negativo e cruza o eixo x em (−2, 0). Em seguida, continua aumentando um pouco antes de diminuir e cruzar o eixo x em (−1, 0). Ele atinge um mínimo local em (1, −6) antes de aumentar e cruzar o eixo x em (2, 0).$

Resposta: Aumentando para$−2<x<−1$ e$x>2$;
Diminuindo para$x<−2$ e$−1<x<2$

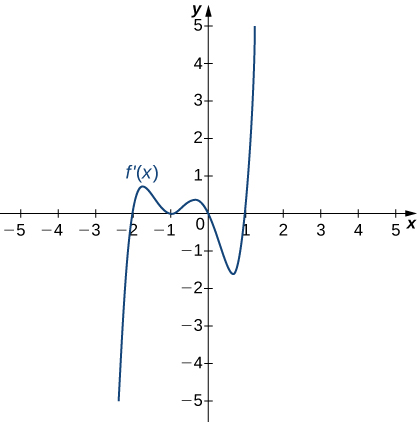
$A função f' (x) é representada graficamente. A função começa com negativo e cruza o eixo x em (−2, 0). Em seguida, continua aumentando um pouco antes de diminuir e tocar o eixo x em (−1, 0). Em seguida, ele aumenta um pouco antes de diminuir e cruzar o eixo x na origem. A função então diminui para um mínimo local antes de aumentar, cruzando o eixo x em (1, 0) e continuando a aumentar.$

10)

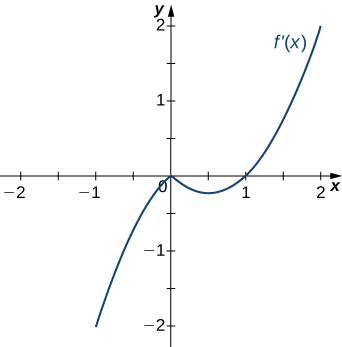
$A função f' (x) é representada graficamente. A função começa com negativo e toca o eixo x na origem. Em seguida, ele diminui um pouco antes de aumentar para cruzar o eixo x em (1, 0) e continuar a aumentar.$

Resposta: Diminuindo para$x<1$,
aumentando para$x>1$

11)

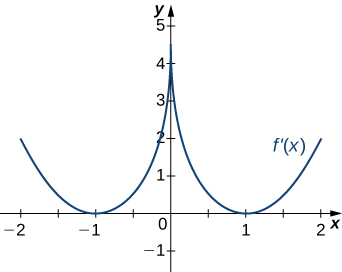
$A função f' (x) é representada graficamente. A função começa positiva e diminui ao tocar o eixo x em (−1, 0). Em seguida, ele aumenta para (0, 4,5) antes de diminuir para tocar o eixo x em (1, 0). Em seguida, a função aumenta.$

12)

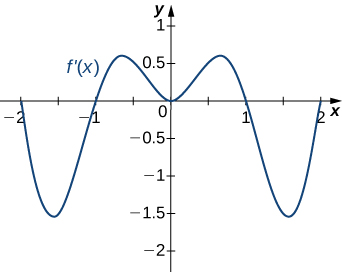
$A função f' (x) é representada graficamente. A função começa em (−2, 0), diminui para (−1,5, −1,5), aumenta para (−1, 0) e continua aumentando antes de diminuir para a origem. Então, o outro lado é simétrico: ou seja, a função aumenta e depois diminui para passar (1, 0). Ele continua diminuindo para (1,5, −1,5) e depois aumenta para (2, 0).$

Resposta: Diminuindo para$−2<x<−1$ e$1<x<2$;
Aumentando para$−1<x<1$ e$x<−2$ e$x>2$

Nos exercícios 13 a 17, analise os gráficos$f',$ e liste todos os intervalos onde

a.$f$ está aumentando e diminuindo e

b. os mínimos e máximos estão localizados.

13)

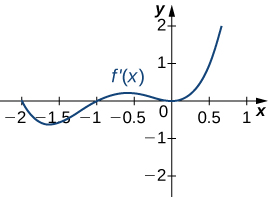
$A função f' (x) é representada graficamente. A função começa em (−2, 0), diminui um pouco e depois aumenta para (−1, 0), continua aumentando antes de diminuir para a origem, momento em que aumenta.$

14)

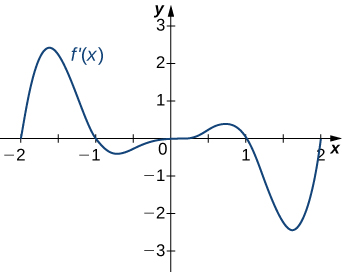
$A função f' (x) é representada graficamente. A função começa em (−2, 0), aumenta e depois diminui para (−1, 0), diminui e depois aumenta para um ponto de inflexão na origem. Em seguida, a função aumenta e diminui para cruzar (1, 0). Ele continua diminuindo e depois aumenta para (2, 0).$

Resposta: a. Aumentando mais$−2<x<−1,\;0<x<1,x>2$, diminuindo sobre$x<−2, \;−1<x<0, \;1<x<2;$
b. Máximos em$x=−1$ e$x=1$, Mínimos em$x=−2$ e e$x=0$ e$x=2$

15)

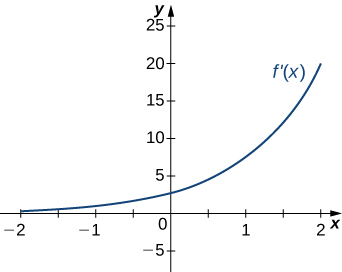
$A função f' (x) é representada graficamente de x = −2 a x = 2. Ele começa próximo de zero em x = −2, mas depois aumenta rapidamente e permanece positivo em todo o comprimento do gráfico.$

16)

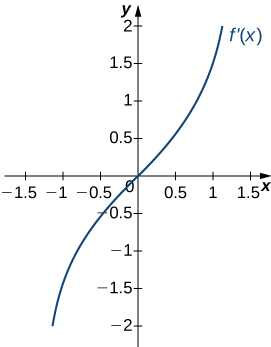
$A função f' (x) é representada graficamente. A função começa com negativo e cruza o eixo x na origem, que é um ponto de inflexão. Em seguida, continua aumentando.$

Resposta: a. Aumentando mais$x>0$, diminuindo acima de$x<0;$
b. Mínimo em$x=0$

17)

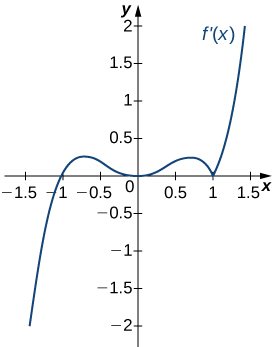
$A função f' (x) é representada graficamente. A função começa com negativo e cruza o eixo x em (−1, 0). Em seguida, continua aumentando um pouco antes de diminuir e tocar o eixo x na origem. Ele aumenta novamente e depois diminui para (1, 0). Em seguida, aumenta.$

Nos exercícios 18 a 22, analise os gráficos de e, em seguida$f'$, liste todos os pontos de inflexão e intervalos$f$ côncavos para cima e côncavos para baixo.

18)

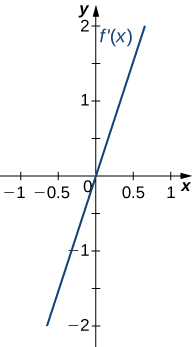
$A função f' (x) é representada graficamente. A função é linear e começa negativa. Ele cruza o eixo x na origem.$

Resposta: Côncavo para todos$x$,
sem pontos de inflexão

19)

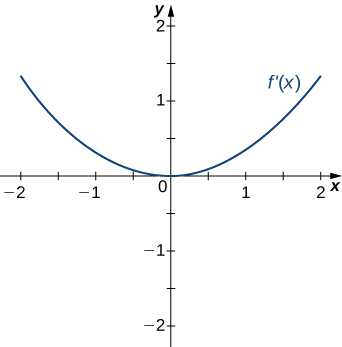
$A função f' (x) é representada graficamente. É uma parábola voltada para cima com 0 como mínimo local.$

20)

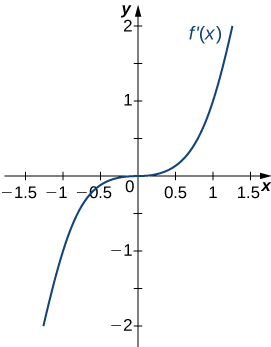
$A função f' (x) é representada graficamente. A função se assemelha ao gráfico de x3: ou seja, ela começa com negativo e cruza o eixo x na origem. Em seguida, continua aumentando.$

Resposta: Côncavo para todos$x$,
sem pontos de inflexão

21)

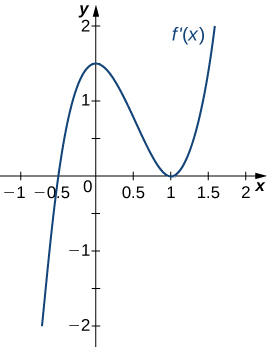
$A função f' (x) é representada graficamente. A função começa com negativo e cruza o eixo x em (−0,5, 0). Em seguida, continua aumentando para (0, 1,5) antes de diminuir e tocar no eixo x em (1, 0). Em seguida, aumenta.$

22)

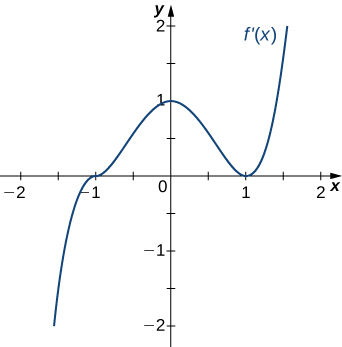
$A função f' (x) é representada graficamente. A função começa com negativo e cruza o eixo x em (−1, 0). Em seguida, continua aumentando até um máximo local em (0, 1), ponto em que diminui e toca o eixo x em (1, 0). Em seguida, aumenta.$

Resposta: Côncavo para cima para$x<0$ e$x>1$,
Côncavo para baixo para$0<x<1$, Pontos
de inflexão em$x=0$ e$x=1$

Para os exercícios 23 a 27, desenhe um gráfico que satisfaça as especificações fornecidas para$x=[−3,3].$ o domínio. A função não precisa ser contínua ou diferenciável.

23)$f(x)>0,\;f'(x)>0$$x>1,\;−3<x<0,\;f'(x)=0$ mais de$0<x<1$

24)$f'(x)>0$$x>2,\;−3<x<−1,\;f'(x)<0$ mais$−1<x<2,\;f''(x)<0$ para todos$x$

Resposta: As respostas variarão

25)$f''(x)<0$ acima do máximo$−1<x<1,\;f''(x)>0,\;−3<x<−1,\;1<x<3,$$x=0,$ local em mínimos locais em$x=±2$

26) Há um máximo local no mínimo$x=2,$ local em$x=1,$ e o gráfico não é côncavo para cima nem côncavo para baixo.

Resposta: As respostas variarão

27) Existem máximos locais em que$x=±1,$ a função é côncava para todos$x$ e a função permanece positiva para todos$x.$

Para os exercícios a seguir, determine

a. intervalos em que$f$ está aumentando ou diminuindo e

b. mínimos e máximos locais de$f$.

28)$f(x)=\sin x+\sin^3x$ acabou$−π<x<π$

Resposta

a. Aumentar em$−\frac{π}{2}<x<\frac{π}{2},$ detrimento da diminuição$x<−\frac{π}{2},\; x>\frac{π}{2}$

b. Máximo local em$x=\frac{π}{2}$; mínimo local em$x=−\frac{π}{2}$

29)$f(x)=x^2+\cos x$

Para o exercício 30, determine

a. intervalos em que$f$ é côncavo para cima ou côncavo para baixo, e

b. os pontos de inflexão de$f$.

30)$f(x)=x^3−4x^2+x+2$

Resposta

a. Côncavo para$x>\frac{4}{3},$ cima para baixo para$x<\frac{4}{3}$

b. Ponto de inflexão em$x=\frac{4}{3}$

Para os exercícios 31 a 37, determine

a. intervalos em que$f$ está aumentando ou diminuindo,

b. mínimos e máximos locais de$f$,

c. intervalos em que$f$ é côncavo para cima e côncavo para baixo, e

d. os pontos de inflexão de$f.$

31)$f(x)=x^2−6x$

32)$f(x)=x^3−6x^2$

Resposta: a. Aumentando$x<0$ e$x>4,$ diminuindo sobre$0<x<4$
b. Máximo em$x=0$, mínimo em$x=4$
c. Côncavo para cima$x>2$, côncavo para baixo para$x<2$
d. Ponto de inflexão em$x=2$

33)$f(x)=x^4−6x^3$

34)$f(x)=x^{11}−6x^{10}$

Resposta: a. Aumentando$x<0$ e$x>\frac{60}{11}$ diminuindo sobre$0<x<\frac{60}{11}$
b. Máximo em$x=0$, mínimo em$x=\frac{60}{11}$
c. Côncavo para baixo para$x<\frac{54}{11}$, côncavo para cima para$x>\frac{54}{11}$
d. Ponto de inflexão em$x=\frac{54}{11}$

(35)$f(x)=x+x^2−x^3$

36)$f(x)=x^2+x+1$

Resposta: a. Aumentando mais$x>−\frac{1}{2}$, diminuindo sobre$x<−\frac{1}{2}$
b. Mínimo em$x=−\frac{1}{2}$
c. Côncavo para cima para todos$x$
d. Sem pontos de inflexão

37)$f(x)=x^3+x^4$

Para os exercícios 38 a 47, determine

a. intervalos em que$f$ está aumentando ou diminuindo,

b. mínimos e máximos locais de$f,$

c. intervalos em que$f$ é côncavo para cima e côncavo para baixo, e

d. os pontos de inflexão de$f.$ Esboce a curva e, em seguida, use uma calculadora para comparar sua resposta. Se você não conseguir determinar a resposta exata analiticamente, use uma calculadora.

38) [T]$f(x)=\sin(πx)−\cos(πx)$ acabou$x=[−1,1]$

Resposta: a. Aumenta em$−\frac{1}{4}<x<\frac{3}{4},$ decréscimos acima$x>\frac{3}{4}$ e$x<−\frac{1}{4}$
b. Mínimo em$x=−\frac{1}{4}$, máximo em$x=\frac{3}{4}$
c. Côncavo para cima$−\frac{3}{4}<x<\frac{1}{4}$, côncavo para baixo para$x<−\frac{3}{4}$ e$x>\frac{1}{4}$
d. Pontos de inflexão em$x=−\frac{3}{4},\;x=\frac{1}{4}$

39) [T]$f(x)=x+\sin(2x)$ acabou$x=[−\frac{π}{2},\frac{π}{2}]$

40) [T]$f(x)=\sin x+\tan x$ acabou$(−\frac{π}{2},\frac{π}{2})$

Resposta: a. Aumentando para todos$x$
b. Sem mínimo ou máximo local
c. Côncavo para cima$x>0$, côncavo para baixo para$x<0$
d. Ponto de inflexão em$x=0$

41) [T]$f(x)=(x−2)^2(x−4)^2$

42) [T]$f(x)=\dfrac{1}{1−x},\quad x≠1$

Resposta: a. Aumentando para todos$x$ quando definido
b. Sem mínimos ou máximos locais
c. Côncavo para cima$x<1$; côncavo para baixo para$x>1$
d. Sem pontos de inflexão no domínio

43) [T]$f(x)=\dfrac{\sin x}{x}$ acabou$x=[-2π,0)∪(0,2π]$

44)$f(x)=\sin(x)e^x$ acabou$x=[−π,π]$

Resposta: a. Aumentando mais$−\frac{π}{4}<x<\frac{3π}{4}$, diminuindo sobre$x>\frac{3π}{4},\;x<−\frac{π}{4}$
b. Mínimo em$x=−\frac{π}{4}$, máximo em$x=\frac{3π}{4}$
c. Côncavo para cima$−\frac{π}{2}<x<\frac{π}{2}$, côncavo para baixo para$x<−\frac{π}{2},\;x>\frac{π}{2}$
d. Pontos de inflexão em$x=±\frac{π}{2}$

45)$f(x)=\ln x\sqrt{x},\quad x>0$

(46)$f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x},\quad x>0$

Resposta: a. Aumentando$x>4,$ decrescente em relação a$0<x<4$
b. Mínimo em$x=4$
c. Côncavo para cima para$0<x<8\sqrt[3]{2}$, côncavo para baixo para$x>8\sqrt[3]{2}$
d. Ponto de inflexão em$x=8\sqrt[3]{2}$

47)$f(x)=\dfrac{e^x}{x},\quad x≠0$

Nos exercícios 48 a 52, interprete as frases em termos de$f,\;f',$ e$f''.$

48) A população está crescendo mais lentamente. Aqui$f$ está a população.

Resposta: $f>0,\;f'>0,\;f''<0$

49) Uma bicicleta acelera mais rápido, mas um carro vai mais rápido. Aqui, a posição da$f=$ bicicleta menos a posição do carro.

50) O avião pousa sem problemas. Aqui$f$ está a altitude do avião.

Resposta: $f>0,\;f'<0,\;f''>0$

51) Os preços das ações estão no auge. Aqui$f$ está o preço das ações.

52) A economia está ganhando velocidade. Aqui$f$ está uma medida da economia, como o PIB.

Resposta: $f>0,\;f'>0,\;f''>0$

Para os exercícios 53 - 57, considere um polinômio de terceiro grau$f(x),$ que tenha as propriedades$f'(1)=0$$f'(3)=0$ e.

Determine se as afirmações a seguir são verdadeiras ou falsas. Justifique sua resposta.

53)$f(x)=0$ para alguns$1≤x≤3$.

54)$f''(x)=0$ para alguns$1≤x≤3$.

Resposta: É verdade, pelo Teorema do Valor Médio

55) Não há máximo absoluto em$x=3$.

56) Se$f(x)$ tem três raízes, então tem ponto de$1$ inflexão.

Resposta: É verdade, examine a derivada

57) Se$f(x)$ tem um ponto de inflexão, então tem três raízes reais.