4.5: Derivadas e a forma de um gráfico
- Page ID
- 188242
- Explique como o sinal da primeira derivada afeta a forma do gráfico de uma função.
- Indique o primeiro teste derivado para pontos críticos.
- Use pontos de concavidade e inflexão para explicar como o sinal da segunda derivada afeta a forma do gráfico de uma função.
- Explique o teste de concavidade para uma função em um intervalo aberto.
- Explique a relação entre uma função e sua primeira e segunda derivadas.
- Indique o segundo teste derivado para extremos locais.
No início deste capítulo, afirmamos que se uma função\(f\) tem um extremo local em um ponto\(c\), então\(c\) deve ser um ponto crítico de\(f\). No entanto, não é garantido que uma função tenha uma extremidade local em um ponto crítico. Por exemplo,\(f(x)=x^3\) tem um ponto crítico\(x=0\) desde que\(f'(x)=3x^2\) é zero em\(x=0\), mas\(f\) não tem um extremo local em\(x=0\). Usando os resultados da seção anterior, agora podemos determinar se um ponto crítico de uma função realmente corresponde a um valor extremo local. Nesta seção, também vemos como a segunda derivada fornece informações sobre a forma de um gráfico ao descrever se o gráfico de uma função se curva para cima ou para baixo.
O primeiro teste derivado
O corolário\(3\) do Teorema do Valor Médio mostrou que se a derivada de uma função for positiva em um intervalo\(I\), a função está aumentando\(I\). Por outro lado, se a derivada da função for negativa em um intervalo\(I\), a função estará diminuindo\(I\) conforme mostrado na figura a seguir.
Uma função contínua\(f\) tem um máximo local no ponto\(c\) se e somente se\(f\) mudar de aumento para decrescente no ponto\(c\). Da mesma forma,\(f\) tem um mínimo local de\(c\) se e somente se\(f\) mudar de decrescente para aumentar em\(c\). Se\(f\) for uma função contínua em um intervalo\(I\) contendo\(c\) e diferenciável sobre\(I\), exceto possivelmente em\(c\), a única maneira de\(f\) mudar de aumento para decrescente (ou vice-versa) em um ponto\(c\) é se\(f'\) as mudanças sinalizarem como \(x\)aumenta através de\(c\). Se\(f\) for diferenciável em\(c\), a única maneira de\(f'\) mudar de sinal à medida que\(x\) aumenta\(c\) é se\(f'(c)=0\). Portanto, para uma função\(f\) que é contínua em um intervalo\(I\) contendo\(c\) e diferenciável\(I\), exceto possivelmente em\(c\), a única maneira de\(f\) mudar de crescente para decrescente (ou vice-versa) é se\(f'(c)=0\) ou\(f'(c)\) é indefinida. Consequentemente, para localizar a extremidade local de uma função\(f\), procuramos pontos\(c\) no domínio\(f\) dessa que\(f'(c)=0\) ou\(f'(c)\) estejam indefinidos. Lembre-se de que esses pontos são chamados de pontos críticos de\(f\).
Observe que não é\(f\) necessário ter um extremo local em um ponto crítico. Os pontos críticos são candidatos apenas aos extremos locais. Na Figura\(\PageIndex{2}\), mostramos que se uma função contínua\(f\) tem um extremo local, ela deve ocorrer em um ponto crítico, mas uma função pode não ter uma extremidade local em um ponto crítico. Mostramos que,\(f\) se houver uma extremidade local em um ponto crítico, o sinal de\(f'\) comutadores\(x\) aumenta nesse ponto.
Usando a Figura\(\PageIndex{2}\), resumimos os principais resultados em relação aos extremos locais.
- Se uma função contínua\(f\) tem um extremo local, ela deve ocorrer em um ponto crítico\(c\).
- A função tem um extremo local no ponto crítico\(c\) se e somente se as\(f'\) chaves derivadas assinarem como\(x\) aumentos\(c\).
- Portanto, para testar se uma função tem um extremo local em um ponto crítico\(c\), devemos determinar o sinal de\(f'(x)\) à esquerda e à direita de\(c\).
Esse resultado é conhecido como o primeiro teste derivado.
Suponha que\(f\) seja uma função contínua em um intervalo\(I\) contendo um ponto crítico\(c\). Se\(f\) for diferenciável\(I\), exceto possivelmente em alguns pontos\(c\), então\(f(c)\) satisfaz uma das seguintes descrições:
- Se\(f'\) mudar de positivo quando\(x<c\) para negativo quando\(x>c\), então\(f(c)\) é um máximo local de\(f\).
- Se\(f'\) as mudanças forem indicadas de negativo quando\(x<c\) para positivo quando\(x>c\), então\(f(c)\) é um mínimo local de\(f\).
- Se\(f'\) tem o mesmo sinal para\(x<c\) e\(x>c\), então não\(f(c)\) é um máximo local nem um mínimo local de\(f\)
Agora, vamos ver como usar essa estratégia para localizar todos os extremos locais para funções específicas.
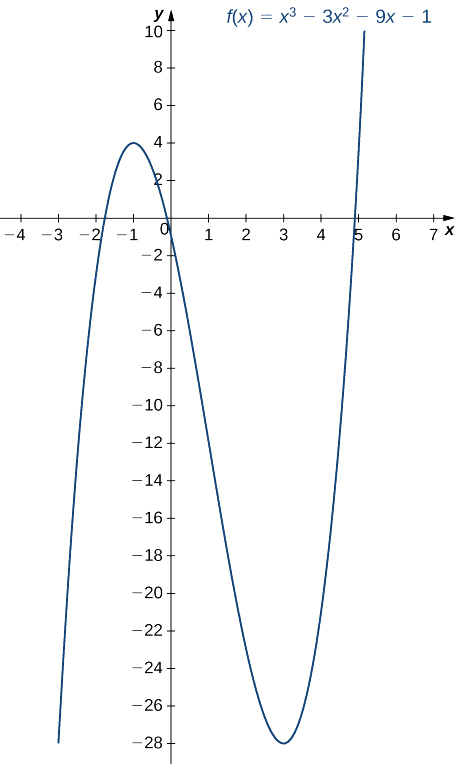
Use o primeiro teste derivado para encontrar a localização de todos os extremos locais para\(f(x)=x^3−3x^2−9x−1.\) Use um utilitário gráfico para confirmar seus resultados.
Solução
Etapa 1. A derivada é:\(f'(x)=3x^2−6x−9.\) Para encontrar os pontos críticos, precisamos descobrir onde\(f'(x)=0.\) Fatorando o polinômio, concluímos que os pontos críticos devem satisfazer
\[3(x^2−2x−3)=3(x−3)(x+1)=0. \nonumber \]
Portanto, os pontos críticos são\(x=3,−1.\) Agora divida o intervalo\((−∞,∞)\) em intervalos menores\((−∞,−1),(−1,3)\) e\((3,∞).\)
Etapa 2. Como\(f'\) é uma função contínua, para determinar o sinal de\(f'(x)\) mais de cada subintervalo, basta escolher um ponto em cada um dos intervalos\((−∞,−1),(−1,3)\)\((3,∞)\) e determinar o sinal de\(f'\) em cada um desses pontos. Por exemplo, vamos escolher\(x=−2\)\(x=0\), e\(x=4\) como pontos de teste.
| Intervalo | Ponto de teste | Sinal de\(f'(x)=3(x−3)(x+1)\) no ponto de teste | Conclusão |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =3 (x−3) (x+1)\) no ponto de teste” style="vertical-align:middle; "> (+) (−) (−) =+ | \(f\)está aumentando. |
| \((−1,3)\) | \(x=0\) | \ (f' (x) =3 (x−3) (x+1)\) no ponto de teste” style="vertical-align:middle; "> (+) (−) (+) =- | \(f\)está diminuindo. |
| \((3,∞)\) | \(x=4\) | \ (f' (x) =3 (x−3) (x+1)\) no ponto de teste” style="vertical-align:middle; "> (+) (+) (+) =+ | \(f\)está aumentando. |
Etapa 3. Como\(f'\) os interruptores passam de positivo para negativo à medida que\(x\) aumenta\(-1\),\(f\) tem um máximo local em\(x=−1\). Como\(f'\) os interruptores passam de negativo para positivo à medida que\(x\) aumenta\(3\),\(f\) tem um mínimo local em\(x=3\). Esses resultados analíticos concordam com o gráfico a seguir.
Use o primeiro teste derivado para localizar todas as extremidades locais para\(f(x)=−x^3+\frac{3}{2}x^2+18x.\)
- Dica
-
Encontre todos os pontos críticos\(f\) e determine os sinais\(f'(x)\) de intervalos específicos determinados pelos pontos críticos.
- Resposta
-
\(f\)tem um mínimo local em\(−2\) e um máximo local em\(3\).
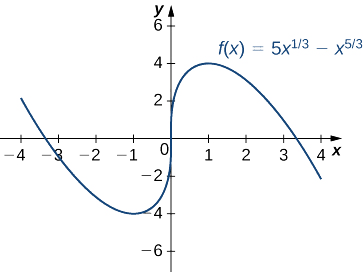
Use o primeiro teste derivado para encontrar a localização de todos os extremos locais para\(f(x)=5x^{1/3}−x^{5/3}.\) Use um utilitário gráfico para confirmar seus resultados.
Solução
Etapa 1. A derivada é
\[f'(x)=\frac{5}{3}x^{−2/3}−\frac{5}{3}x^{2/3}=\frac{5}{3x^{2/3}}−\frac{5x^{2/3}}{3}=\frac{5−5x^{4/3}}{3x^{2/3}}=\frac{5(1−x^{4/3})}{3x^{2/3}}.\nonumber \]
A derivada\(f'(x)=0\) quando\(1−x^{4/3}=0.\) Portanto,\(f'(x)=0\) em\(x=±1\). A derivada\(f'(x)\) é indefinida em\(x=0.\) Portanto, temos três pontos críticos:\(x=0\)\(x=1\),,\(x=−1\) e. Consequentemente,\((−∞,∞)\) divida o intervalo em intervalos menores\((−∞,−1),\,(−1,0),\,(0,1)\),\((1,∞)\) e.
Etapa 2: Como\(f'\) é contínuo em cada subintervalo, basta escolher um ponto de teste\(x\) em cada um dos intervalos da etapa 1 e determinar o sinal de\(f'\) em cada um desses pontos. Os pontos\(x=−2,\,x=−\frac{1}{2},\,x=\frac{1}{2}\) e\(x=2\) são pontos de teste para esses intervalos.
| Intervalo | Ponto de teste | Sinal de\(f'(x)=\frac{5(1−x^{4/3})}{3x^{2/3}}\) no ponto de teste | Conclusão |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) no ponto de teste” style="vertical-align:middle; ">\(\frac{(+)(−)}{+}=−\) | \(f\)está diminuindo. |
| \((−1,0)\) | \(x=−\frac{1}{2}\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) no ponto de teste” style="vertical-align:middle; ">\(\frac{(+)(+)}{+}=+\) | \(f\)está aumentando. |
| \((0,1)\) | \(x=\frac{1}{2}\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) no ponto de teste” style="vertical-align:middle; ">\(\frac{(+)(+)}{+}=+\) | \(f\)está aumentando. |
| \((1,∞)\) | \(x=2\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) no ponto de teste” style="vertical-align:middle; ">\(\frac{(+)(−)}{+}=−\) | \(f\)está diminuindo. |
Etapa 3: Como\(f\) está diminuindo ao longo do intervalo\((−∞,−1)\) e aumentando ao longo do intervalo\((−1,0)\),\(f\) tem um mínimo local em\(x=−1\). Como\(f\) está aumentando ao longo do intervalo\((−1,0)\) e do intervalo\((0,1)\),\(f\) não tem um extremo local em\(x=0\). Como\(f\) está aumentando ao longo do intervalo\((0,1)\) e diminuindo ao longo do intervalo\((1,∞)\),\(f\) tem um máximo local em\(x=1\). Os resultados analíticos concordam com o gráfico a seguir.
Use o primeiro teste derivado para encontrar todos os extremos locais para\(f(x)=\dfrac{3}{x−1}\).
- Dica
-
O único ponto crítico do\(f\) é\(x=1.\)
- Resposta
-
\(f\)não tem extremos locais porque\(f'\) não muda de sinal\(x=1\).
Concavidade e pontos de inflexão
Agora sabemos como determinar onde uma função está aumentando ou diminuindo. No entanto, há outra questão a ser considerada em relação à forma do gráfico de uma função. Se o gráfico se curva, ele se curva para cima ou para baixo? Essa noção é chamada de concavidade da função.
A figura\(\PageIndex{5a}\) mostra uma função\(f\) com um gráfico que se curva para cima. À medida que\(x\) aumenta, a inclinação da reta tangente aumenta. Assim, como a derivada aumenta à medida que\(x\) aumenta,\(f'\) é uma função crescente. Dizemos que essa função\(f\) é côncava para cima. A figura\(\PageIndex{5b}\) mostra uma função\(f\) que se curva para baixo. À medida que\(x\) aumenta, a inclinação da reta tangente diminui. Como a derivada diminui à medida que\(x\) aumenta,\(f'\) é uma função decrescente. Dizemos que essa função\(f\) é côncava para baixo.
\(f\)Seja uma função que seja diferenciável em um intervalo aberto\(I\). Se\(f'\) está aumentando\(I\), dizemos que\(f\) é côncavo para cima\(I\). Se\(f'\) está diminuindo\(I\), dizemos que\(f\) é côncavo para baixo\(I\).
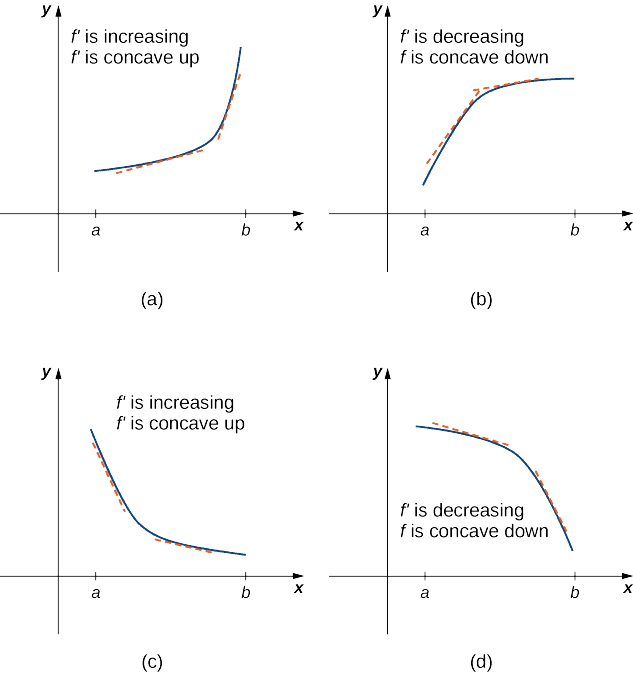
Em geral, sem ter o gráfico de uma função\(f\), como podemos determinar sua concavidade? Por definição, uma função\(f\) é côncava para cima se\(f'\) estiver aumentando. Do Corolário\(3\), sabemos que se\(f'\) é uma função diferenciável, então\(f'\) está aumentando se for derivada\(f''(x)>0\). Portanto, uma função\(f\) que é duas vezes diferenciável é côncava para cima quando\(f''(x)>0\). Da mesma forma, uma função\(f\) é côncava para baixo se\(f'\) estiver diminuindo. Sabemos que uma função diferenciável\(f'\) está diminuindo se for derivada\(f''(x)<0\). Portanto, uma função duas vezes diferenciável\(f\) é côncava para baixo quando\(f''(x)<0\). A aplicação dessa lógica é conhecida como teste de concavidade.
\(f\)Seja uma função que seja duas vezes diferenciável em um intervalo\(I\).
- Se for\(f''(x)>0\) para todos\(x∈I\), então\(f\) é côncavo para cima\(I\)
- Se for\(f''(x)<0\) para todos\(x∈I,\), então\(f\) é côncavo para baixo\(I\).
Concluímos que podemos determinar a concavidade de uma função\(f\) observando a segunda derivada de\(f\). Além disso, observamos que uma função\(f\) pode alternar a concavidade (Figura\(\PageIndex{6}\)). No entanto, uma função contínua pode alternar a concavidade somente em um ponto\(x\) se\(f''(x)=0\) ou\(f''(x)\) for indefinido. Consequentemente, para determinar os intervalos em que uma função\(f\) é côncava para cima e côncava para baixo, procuramos os valores de\(x\) onde\(f''(x)=0\) ou\(f''(x)\) está indefinido. Quando determinamos esses pontos, dividimos o domínio de\(f\) em intervalos menores e determinamos o sinal de\(f''\) sobre cada um desses intervalos menores. Se\(f''\) as mudanças assinarem quando passamos por um ponto\(x\), então\(f\) muda a concavidade. É importante lembrar que uma função\(f\) pode não mudar a concavidade em um ponto,\(x\) mesmo se\(f''(x)=0\) ou não\(f''(x)\) estiver definida. Se, no entanto,\(f\) muda a concavidade em um ponto\(a\) e\(f\) é contínuo em\(a\), dizemos que o ponto\((a,f(a))\) é um ponto de inflexão de\(f\).
Se\(f\) é contínuo em\(a\) e\(f\) muda a concavidade em\(a\), o ponto\((a, \,f(a))\) é um ponto de inflexão de\(f\).
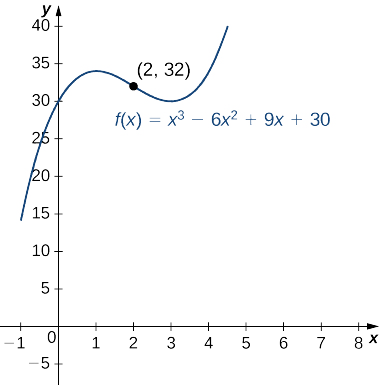
Para a função,\(f(x)=x^3−6x^2+9x+30,\) determine todos os intervalos onde\(f\) é côncavo para cima e todos os intervalos onde\(f\) é côncavo para baixo. Liste todos os pontos de inflexão para\(f\). Use um utilitário gráfico para confirmar seus resultados.
Solução
Para determinar a concavidade, precisamos encontrar a segunda derivada.\(f''(x).\) A primeira derivada é\(f'(x)=3x^2−12x+9,\) então a segunda derivada é\(f''(x)=6x−12.\) Se a função muda de concavidade, ela ocorre quando\(f''(x)=0\) ou\(f''(x)\) é indefinida. Como\(f''\) é definido para todos os números reais\(x\), precisamos apenas descobrir onde\(f''(x)=0\). Resolvendo a equação\(6x−12=0\), vemos que\(x=2\) é o único lugar onde\(f\) poderia mudar a concavidade. Agora testamos pontos ao longo dos intervalos\((−∞,2)\) e\((2,∞)\) determinamos a concavidade de\(f\). Os pontos\(x=0\) e\(x=3\) são pontos de teste para esses intervalos.
| Intervalo | Ponto de teste | Sinal de\(f''(x)=6x−12\) no ponto de teste | Conclusão |
|---|---|---|---|
| \((−∞,2)\) | \(x=0\) | \ (f "(x) =6x−12\) no ponto de teste” style="vertical-align:middle; ">− | \(f\)é côncavo para baixo |
| \((2,∞)\) | \(x=3\) | \ (f "(x) =6x−12\) no ponto de teste” style="vertical-align:middle; ">+ | \(f\)é côncavo para cima |
Concluímos que\(f\) é côncavo para baixo sobre o intervalo\((−∞,2)\) e côncavo para cima sobre o intervalo\((2,∞)\). Como\(f\) muda a concavidade em\(x=2\), o ponto\((2,f(2))=(2,32)\) é um ponto de inflexão. A figura\(\PageIndex{7}\) confirma os resultados analíticos.
Para\(f(x)=−x^3+\frac{3}{2}x^2+18x\), encontre todos os intervalos onde\(f\) é côncavo para cima e todos os intervalos onde\(f\) está côncavo para baixo.
- Dica
-
Descubra onde\(f''(x)=0\)
- Resposta
-
\(f\)é côncavo para cima sobre o intervalo\((−∞,\frac{1}{2})\) e côncavo para baixo sobre o intervalo\((\frac{1}{2},∞)\)
Agora resumimos, na Tabela\(\PageIndex{4}\), as informações que a primeira e a segunda derivadas de uma função\(f\) fornecem sobre o gráfico e ilustramos essas informações na Figura\(\PageIndex{8}\).\(f\)
| Sinal de\(f'\) | Sinal de\(f''\) | Está\(f\) aumentando ou diminuindo? | Concavidade |
|---|---|---|---|
| \ (f'\)” style="vertical-align:middle; ">Positivo | \ (f "\)” style="vertical-align:middle; ">Positivo | \ (f\) aumentando ou diminuindo?” style="vertical-align:middle; ">Aumentando | Côncavo para cima |
| \ (f'\)” style="vertical-align:middle; ">Positivo | \ (f "\)” style="vertical-align:middle; ">Negativo | \ (f\) aumentando ou diminuindo?” style="vertical-align:middle; ">Aumentando | Côncavo para baixo |
| \ (f'\)” style="vertical-align:middle; ">Negativo | \ (f "\)” style="vertical-align:middle; ">Positivo | \ (f\) aumentando ou diminuindo?” style="vertical-align:middle; ">Diminuindo | Côncavo para cima |
| \ (f'\)” style="vertical-align:middle; ">Negativo | \ (f "\)” style="vertical-align:middle; ">Negativo | \ (f\) aumentando ou diminuindo?” style="vertical-align:middle; ">Diminuindo | Côncavo para baixo |
O segundo teste derivado
O primeiro teste derivado fornece uma ferramenta analítica para encontrar extremos locais, mas a segunda derivada também pode ser usada para localizar valores extremos. Usar a segunda derivada às vezes pode ser um método mais simples do que usar a primeira derivada.
Sabemos que se uma função contínua tem um extremo local, ela deve ocorrer em um ponto crítico. No entanto, uma função não precisa ter uma extremidade local em um ponto crítico. Aqui, examinamos como o segundo teste de derivada pode ser usado para determinar se uma função tem um extremo local em um ponto crítico. \(f\)Seja uma função duas vezes diferenciável, tal que\(f'(a)=0\) e\(f''\) seja contínua em um intervalo aberto\(I\) contendo\(a\). Suponha\(f''(a)<0\). Uma vez que\(f''\) é contínuo\(I, f''(x)<0\) para todos\(x∈I\) (Figura\(\PageIndex{9}\)). Então, por Corolário\(3\),\(f'\) uma função decrescente está encerrada\(I\). Desde então\(f'(a)=0\), concluímos que, para todos,\(x∈I, \,f'(x)>0\) se\(x<a\) e\(f'(x)<0\) se\(x>a\). Portanto, pelo primeiro teste derivado,\(f\) tem um máximo local em\(x=a\).
Por outro lado, suponha que exista um ponto\(b\) como esse\(f'(b)=0\), mas\(f''(b)>0\). Uma vez que\(f''\) é contínuo em um intervalo aberto\(I\) contendo\(b\), então\(f''(x)>0\) para todos\(x∈I\) (Figura\(\PageIndex{9}\)). Então, por Corolário\(3\),\(f'\) uma função crescente acabou\(I\). Desde então\(f'(b)=0\), concluímos que, para todos\(x∈I\),\(f'(x)<0\) se\(x<b\) e\(f'(x)>0\) se\(x>b\). Portanto, pelo primeiro teste derivado,\(f\) tem um mínimo local em\(x=b.\)
Suponha que\(f'(c)=0\) e\(f''\) seja contínuo em um intervalo contendo\(c\).
- Se\(f''(c)>0\), então\(f\) tem um mínimo local em\(c\).
- Se\(f''(c)<0\), então\(f\) tem um máximo local em\(c\).
- \(f''(c)=0,\)Em caso afirmativo, o teste é inconclusivo.
Observe que, para o caso iii. quando\(f''(c)=0\), então\(f\) pode ter um máximo local, mínimo local ou nenhum em\(c\). Por exemplo, as funções\(f(x)=x^3, \; f(x)=x^4,\) e\(f(x)=−x^4\) todas têm pontos críticos em\(x=0\). Em cada caso, a segunda derivada é zero em\(x=0\). No entanto, a função\(f(x)=x^4\) tem um mínimo local em\(x=0\),\(x=0\) enquanto a função\(f(x)=−x^4\) tem um máximo local em e a função\(f(x)=x^3\) não tem um extremo local em\(x=0\).
Vamos agora ver como usar o segundo teste derivado para determinar se\(f\) tem um máximo local ou mínimo local em um ponto crítico\(c\) onde\(f'(c)=0.\)
Use a segunda derivada para encontrar a localização de todos os extremos locais para\(f(x)=x^5−5x^3.\)
Solução
Para aplicar o segundo teste derivado, primeiro precisamos encontrar pontos críticos\(c\) onde\(f'(c)=0\). A derivada é\(f'(x)=5x^4−15x^2\). Portanto,\(f'(x)=5x^4−15x^2=5x^2(x^2−3)=0\) quando\(x=0,\,±\sqrt{3}\).
Para determinar se\(f\) tem uma extremidade local em algum desses pontos, precisamos avaliar o sinal de\(f''\) nesses pontos. A segunda derivada é
\(f''(x)=20x^3−30x=10x(2x^2−3).\)
Na tabela a seguir, avaliamos a segunda derivada em cada um dos pontos críticos e usamos o teste da segunda derivada para determinar se\(f\) tem um máximo local ou mínimo local em algum desses pontos.
| \(x\) | \(f''(x)\) | Conclusão |
|---|---|---|
| \ (x\) ">\(−\sqrt{3}\) | \ (f "(x)\)" >\(−30\sqrt{3}\) | Máximo local |
| \ (x\) ">\(0\) | \ (f "(x)\)" >\(0\) | O segundo teste derivado é inconclusivo |
| \ (x\) ">\(\sqrt{3}\) | \ (f "(x)\)" >\(30\sqrt{3}\) | Mínimo local |
Pelo segundo teste derivado, concluímos que\(f\) tem um máximo local em\(x=−\sqrt{3}\) e\(f\) tem um mínimo local em\(x=\sqrt{3}\). O segundo teste derivado é inconclusivo em\(x=0\). Para determinar se\(f\) tem uma extremidade local em,\(x=0,\) aplicamos o primeiro teste derivado. Para avaliar o sinal de\(f'(x)=5x^2(x^2−3)\) para\(x∈(−\sqrt{3},0)\) e\(x∈(0,\sqrt{3})\), seja\(x=−1\) e\(x=1\) seja os dois pontos de teste. Desde\(f'(−1)<0\) e\(f'(1)<0\), concluímos que\(f\) está diminuindo em ambos os intervalos e, portanto,\(f\) não tem uma extremidade local em,\(x=0\) conforme mostrado no gráfico a seguir.
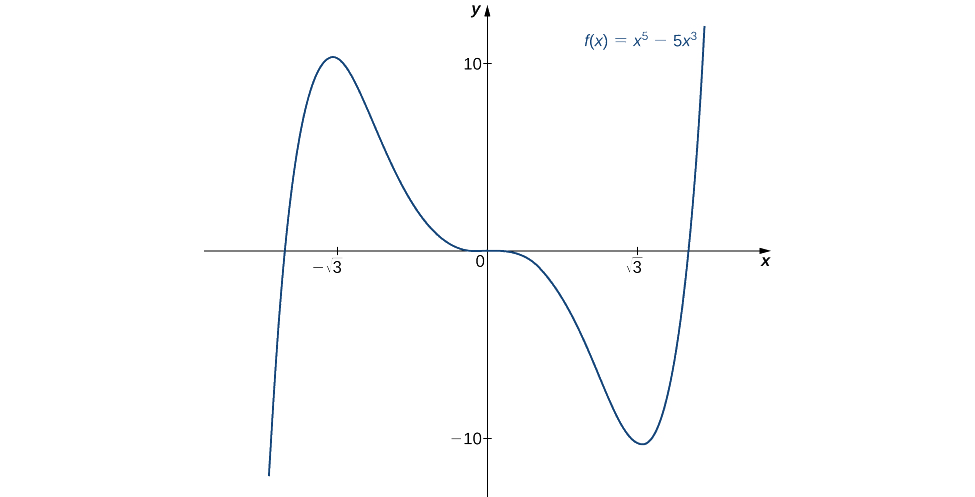
Considere a função\(f(x)=x^3−(\frac{3}{2})x^2−18x\). Os pontos\(c=3,\,−2\) satisfazem\(f'(c)=0\). Use o segundo teste derivado para determinar se\(f\) tem um máximo local ou mínimo local nesses pontos.
- Dica
-
\(f''(x)=6x−3\)
- Resposta
-
\(f\)tem um máximo local em\(−2\) e um mínimo local em\(3\).
Agora desenvolvemos as ferramentas necessárias para determinar onde uma função está aumentando e diminuindo, bem como adquirimos uma compreensão da forma básica do gráfico. Na próxima seção, discutiremos o que acontece com uma função, pois\(x→±∞.\) Nesse ponto, temos ferramentas suficientes para fornecer gráficos precisos de uma grande variedade de funções.
Conceitos-chave
- Se\(c\) for um ponto crítico de\(f\) e\(f'(x)>0\) para\(x<c\) e\(f'(x)<0\) para\(x>c\), então\(f\) tem um máximo local em\(c\).
- Se\(c\) é um ponto crítico de\(f\) e\(f'(x)<0\) para\(x<c\) e\(f'(x)>0\) para\(x>c,\) então\(f\) tem um mínimo local em\(c\).
- Se estiver\(f''(x)>0\) em um intervalo\(I\), então\(f\) é côncavo para cima\(I\).
- Se estiver\(f''(x)<0\) em um intervalo\(I\), então\(f\) é côncavo para baixo\(I\).
- Se\(f'(c)=0\) e\(f''(c)>0\), então\(f\) tem um mínimo local em\(c\).
- Se\(f'(c)=0\) e\(f''(c)<0\), então\(f\) tem um máximo local em\(c\).
- Se\(f'(c)=0\) e\(f''(c)=0\), então avalie\(f'(x)\) em um ponto de teste\(x\) à esquerda\(c\) e um ponto de teste\(x\) à direita de\(c\), para determinar se\(f\) tem uma extremidade local em\(c\).
Glossário
- côncavo para baixo
- se\(f\) é diferenciável em um intervalo\(I\) e\(f'\) está diminuindo\(I\), então\(f\) é côncavo para baixo\(I\)
- côncavo para cima
- se\(f\) é diferenciável em um intervalo\(I\) e\(f'\) está aumentando\(I\), então\(f\) é côncavo acima\(I\)
- concavidade
- a curva ascendente ou descendente do gráfico de uma função
- teste de concavidade
- suponha que\(f\) seja duas vezes diferenciável em um intervalo\(I\); se\(f''>0\) terminar\(I\), então\(f\) é côncavo para cima\(I\); se\(f''<\) terminar\(I\), então\(f\) é côncavo para baixo\(I\)
- primeiro teste derivado
- \(f\)seja uma função contínua em um intervalo\(I\) contendo um ponto crítico\(c\) tal que\(f\) seja diferenciável,\(I\) exceto possivelmente em\(c\); se\(f'\) mudar de sinal de positivo para negativo à medida que\(x\) aumenta\(c\), então \(f\)tem um máximo local em\(c\); se\(f'\) as mudanças de sinal de negativo para positivo à medida que\(x\) aumenta\(c\), então\(f\) tem um mínimo local em\(c\); se\(f'\) não mudar de sinal à medida que\(x\) aumenta\(c\), então\(f\) não tem uma extremidade local em\(c\)
- ponto de inflexão
- se\(f\) é contínuo em\(c\) e\(f\) muda a concavidade em\(c\), o ponto\((c,f(c))\) é um ponto de inflexão de\(f\)
- segundo teste de derivada
- suponha que\(f'(c)=0\) e\(f'\) 'seja contínuo em um intervalo contendo\(c\); if\(f''(c)>0\), então\(f\) tem um mínimo local em\(c\); if\(f''(c)<0\), então\(f\) tem um máximo local em\(c\); if\(f''(c)=0\), então o teste é inconclusivo


