4.4: O teorema do valor médio

Last updated
Save as PDF

Page ID: 188354

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Explique o significado do teorema de Rolle.
Descreva a importância do Teorema do Valor Médio.
Declare três consequências importantes do Teorema do Valor Médio.

O Teorema do Valor Médio é um dos teoremas mais importantes do cálculo. Examinamos algumas de suas implicações no final desta seção. Primeiro, vamos começar com um caso especial do Teorema do Valor Médio, chamado teorema de Rolle.

Teorema de Rolle

Informalmente, o teorema de Rolle afirma que, se as saídas de uma função diferenciável$f$ forem iguais nos pontos finais de um intervalo, então deve haver um ponto interior$c$ onde$f'(c)=0$. A figura$\PageIndex{1}$ ilustra esse teorema.

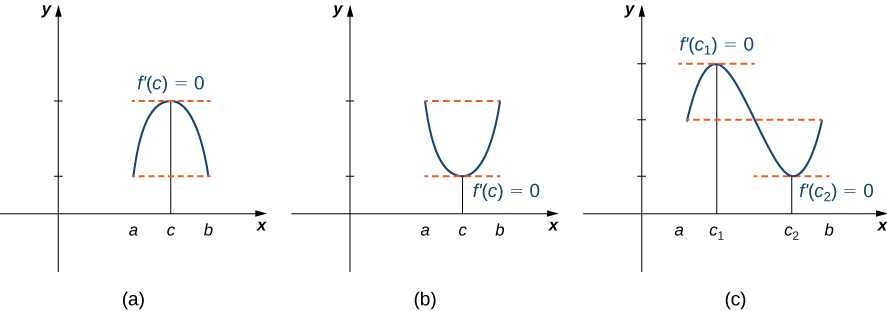
A figura é dividida em três partes rotuladas a, b e c. A Figura a mostra o primeiro quadrante com os valores a, c e b marcados no eixo x. Uma parábola voltada para baixo é desenhada de forma que seus valores em a e b sejam os mesmos. O ponto c é o máximo global e observa-se que f' (c) = 0. A Figura b mostra o primeiro quadrante com os valores a, c e b marcados no eixo x. Uma parábola voltada para cima é desenhada de forma que seus valores em a e b sejam os mesmos. O ponto c é o mínimo global e observa-se que f' (c) = 0. A Figura c mostra o primeiro quadrante com os pontos a, c1, c2 e b marcados no eixo x. Um período de uma onda senoidal é desenhado de forma que seus valores em a e b sejam iguais. O ponto c1 é o máximo global e observa-se que f' (c1) = 0. O ponto c2 é o mínimo global e observa-se que f' (c2) = 0. — Figura$\PageIndex{1}$: Se uma função diferenciável$f$ satisfaz$f(a)=f(b)$, sua derivada deve ser zero em algum ponto (s) entre$a$$b$ e.

Teorema de Rolle

$f$Seja uma função contínua no intervalo fechado$[a,b]$ e diferenciável no intervalo aberto, de$(a,b)$ forma que$f(a)=f(b)$. Existe então pelo menos um$c∈(a,b)$ desses$f'(c)=0.$

Prova

$k=f(a)=f(b).$Vamos considerar três casos:

$f(x)=k$para todos$x∈(a,b).$
Existe$x∈(a,b)$ tal que$f(x)>k.$
Existe$x∈(a,b)$ tal que$f(x)<k.$

Caso 1: Se for$f(x)=k$ para todos$x∈(a,b)$, então$f'(x)=0$ para todos$x∈(a,b).$

Caso 2: Como$f$ é uma função contínua sobre o intervalo fechado e limitado$[a,b]$, pelo teorema do valor extremo, ela tem um máximo absoluto. Além disso,$x∈(a,b)$ como existe um ponto em que$f(x)>k$, o máximo absoluto é maior que$k$. Portanto, o máximo absoluto não ocorre em nenhum dos pontos finais. Como resultado, o máximo absoluto deve ocorrer em um ponto interno$c∈(a,b)$. Porque$f$ tem um máximo em um ponto$c$ interior e$f$ é diferenciável em$c$, pelo teorema de Fermat,$f'(c)=0.$

Caso 3: O caso em que$x∈(a,b)$$f(x)<k$ existe um ponto semelhante ao caso 2, com o máximo substituído pelo mínimo.

□

Um ponto importante sobre o teorema de Rolle é que a diferenciabilidade da função$f$ é crítica. Se não$f$ for diferenciável, mesmo em um único ponto, o resultado pode não se sustentar. Por exemplo, a função$f(x)=|x|−1$ é contínua sobre$[−1,1]$ e$f(−1)=0=f(1)$, mas$f'(c)≠0$ para qualquer uma,$c∈(−1,1)$ conforme mostrado na figura a seguir.

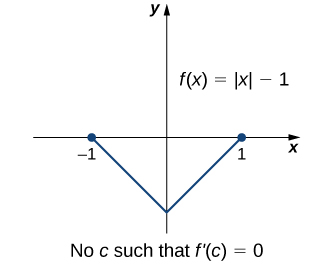
A função f (x) = |x| − 1 é representada graficamente. É mostrado que f (1) = f (−1), mas nota-se que não existe c tal que f' (c) = 0. — Figura$\PageIndex{2}$: Como não$f(x)=|x|−1$ é diferenciável em$x=0$, as condições do teorema de Rolle não são satisfeitas. Na verdade, a conclusão não se sustenta aqui; não existe$c∈(−1,1)$ tal que$f'(c)=0.$

Vamos agora considerar funções que satisfazem as condições do teorema de Rolle e calcular explicitamente os pontos$c$ em que$f'(c)=0.$

Exemplo$\PageIndex{1}$: Using Rolle’s Theorem

Para cada uma das funções a seguir, verifique se a função satisfaz os critérios estabelecidos no teorema de Rolle e encontre todos os valores$c$ no intervalo fornecido onde$f'(c)=0.$

$f(x)=x^2+2x$acabou$[−2,0]$
$f(x)=x^3−4x$acabou$[−2,2]$

Solução

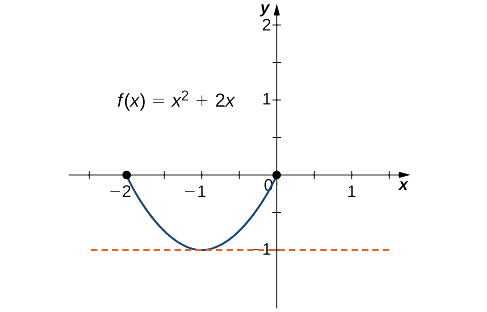
a. Como$f$ é um polinômio, é contínuo e diferenciável em todos os lugares. Além disso,$f(−2)=0=f(0).$ Portanto,$f$ satisfaz os critérios do teorema de Rolle. Concluímos que existe pelo menos um valor$c∈(−2,0)$ desse tipo$f'(c)=0$. Como$f'(x)=2x+2=2(x+1),$ vemos, isso$f'(c)=2(c+1)=0$ implica$c=−1$, conforme mostrado no gráfico a seguir.

A função f (x) = x2 +2x é representada graficamente. É mostrado que f (0) = f (−2), e uma linha horizontal tracejada é desenhada no mínimo absoluto em (−1, −1). — Figura$\PageIndex{3}$: Essa função é contínua e diferenciável sobre [−2,0],$f'(c)=0$ quando$c=−1$.

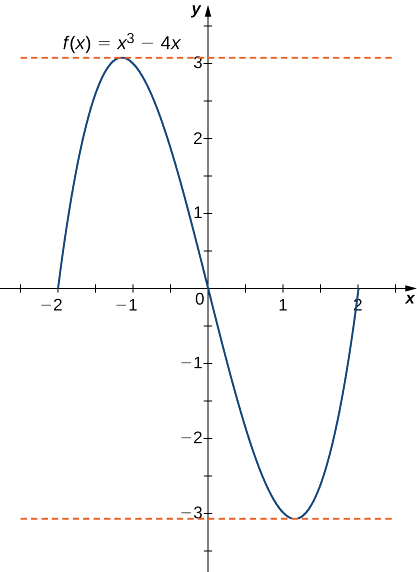
b. Como na parte a.$f$ é um polinômio e, portanto, é contínuo e diferenciável em todos os lugares. Além disso, dito$f(−2)=0=f(2).$ isso,$f$ satisfaz os critérios do teorema de Rolle. Diferenciando, descobrimos que$f'(x)=3x^2−4.$ Portanto,$f'(c)=0$ quando$x=±\frac{2}{\sqrt{3}}$. Ambos os pontos estão no intervalo e$[−2,2]$, portanto, ambos os pontos satisfazem a conclusão do teorema de Rolle, conforme mostrado no gráfico a seguir.

A função f (x) = x3 — 4x é representada graficamente. É óbvio que f (2) = f (−2) = f (0). As linhas horizontais tracejadas são desenhadas em x = ± 2/raiz quadrada de 3, que são o máximo e o mínimo locais. — Figura$\PageIndex{4}$: Para este polinômio acima de$[−2,2], f'(c)=0$ at$x=±2/\sqrt{3}$.

Exercício$\PageIndex{1}$

Verifique se a função$f(x)=2x^2−8x+6$ definida ao longo do intervalo$[1,3]$ satisfaz as condições do teorema de Rolle. Encontre todos os pontos$c$ garantidos pelo teorema de Rolle.

Dica: Encontre todos os valores$c$, onde$f'(c)=0$.

Resposta: $c=2$

O teorema do valor médio e seu significado

O teorema de Rolle é um caso especial do Teorema do Valor Médio. No teorema de Rolle, consideramos funções diferenciáveis$f$ que são zero nos pontos finais. O Teorema do Valor Médio generaliza o teorema de Rolle considerando funções que não são necessariamente zero nos pontos finais. Consequentemente, podemos ver o Teorema do Valor Médio como uma versão inclinada do teorema de Rolle (Figura$\PageIndex{5}$). O Teorema do Valor Médio afirma que, se$f$ for contínuo no intervalo fechado$[a,b]$ e diferenciável no intervalo aberto$(a,b)$, existe um ponto$c∈(a,b)$ tal que a reta tangente ao gráfico de$f$ at$c$ é paralela à linha secante que se conecta $(a,f(a))$e$(b,f(b)).$

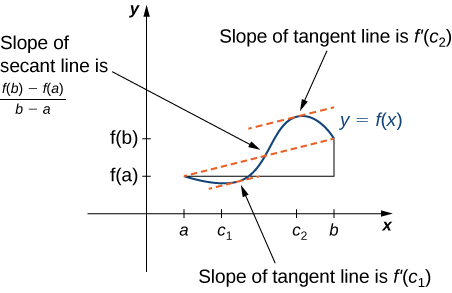
Uma função vagamente sinusoidal y = f (x) é desenhada. No eixo x, a, c1, c2 e b estão marcados. No eixo y, f (a) e f (b) estão marcados. A função f (x) começa em (a, f (a)), diminui para c1, aumenta para c2 e depois diminui para (b, f (b)). Uma linha secante é traçada entre (a, f (a)) e (b, f (b)), e nota-se que essa linha tem inclinação (f (b) — f (a))/(b − a). As linhas tangentes em c1 e c2 são desenhadas e essas linhas são paralelas à linha secante. Note-se que as inclinações dessas retas tangentes são f' (c1) e f' (c2), respectivamente. — Figura$\PageIndex{5}$: O Teorema do Valor Médio diz que, para uma função que atende às suas condições, em algum ponto a reta tangente tem a mesma inclinação da linha secante entre as extremidades. Para esta função, existem dois valores$c_1$ e$c_2$ tal que a reta tangente a$f$ at$c_1$ e$c_2$ tem a mesma inclinação da linha secante.

Teorema do valor médio

$f$Seja contínuo no intervalo fechado$[a,b]$ e diferenciável no intervalo aberto$(a,b)$. Então, existe pelo menos um ponto$c∈(a,b)$ tal que

\[f'(c)=\frac{f(b)−f(a)}{b−a} \nonumber \]

Prova

A prova segue do teorema de Rolle ao introduzir uma função apropriada que satisfaz os critérios do teorema de Rolle. Considere a linha de conexão$(a,f(a))$ e$(b,f(b)).$ uma vez que a inclinação dessa linha é

\[\frac{f(b)−f(a)}{b−a} \nonumber \]

e a linha passa pelo ponto em que$(a,f(a)),$ a equação dessa linha pode ser escrita como

\[y=\frac{f(b)−f(a)}{b−a}(x−a)+f(a). \nonumber \]

Vamos$g(x)$ indicar a diferença vertical entre o ponto$(x,f(x))$ e o ponto$(x,y)$ nessa linha. Portanto,

\[g(x)=f(x)−\left[\frac{f(b)−f(a)}{b−a}(x−a)+f(a)\right]. \nonumber \]

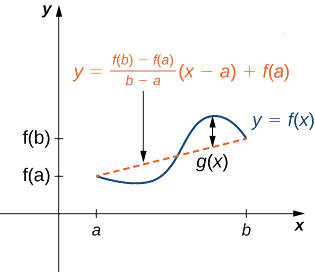$Curva ascendente, mas oscilante, Y é igual a F de X com linha secante Y igual a F de B menos F de A em todo B menos A mais F de A, a distância entre a curva oscilante e a linha é G de X$ Figura$\PageIndex{6}$: O valor$g(x)$ é a diferença vertical entre o ponto$(x,f(x))$ e o ponto$(x,y)$ na linha secante que conecta$(a,f(a))$$(b,f(b))$ e.

Como o gráfico de$f$ cruza a linha secante quando$x=a$ e$x=b$, vemos isso$g(a)=0=g(b)$. Como$f$ é uma função diferenciável encerrada$(a,b)$, também$g$ é uma função diferenciável encerrada$(a,b)$. Além disso, uma vez que$f$$[a,b], \, g$ é contínuo, também é contínuo$[a,b]$. Portanto,$g$ satisfaz os critérios do teorema de Rolle. Consequentemente, existe um ponto$c∈(a,b)$ tal que$g'(c)=0.$ Desde

\[g'(x)=f'(x)−\frac{f(b)−f(a)}{b−a}, \nonumber \]

nós vemos isso

\[g'(c)=f'(c)−\frac{f(b)−f(a)}{b−a}. \nonumber \]

Uma vez$g'(c)=0,$ que concluímos que

\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

□

No próximo exemplo, mostramos como o Teorema do Valor Médio pode ser aplicado à função$f(x)=\sqrt{x}$ durante o intervalo$[0,9]$. O método é o mesmo para outras funções, embora às vezes tenha consequências mais interessantes.

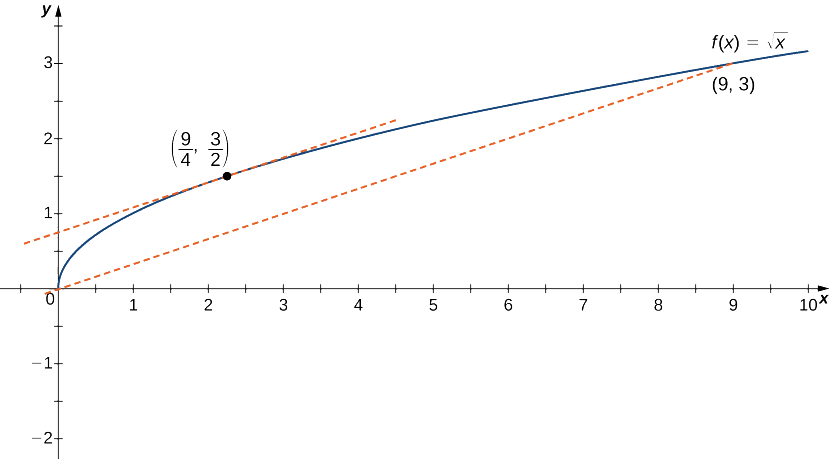
Exemplo$\PageIndex{2}$: Verifying that the Mean Value Theorem Applies

Para$f(x)=\sqrt{x}$ além do intervalo$[0,9]$, mostre que$f$ satisfaz a hipótese do Teorema do Valor Médio e, portanto, existe pelo menos um valor$c∈(0,9)$ igual à inclinação da linha que$f′(c)$ conecta$(0,f(0))$$(9,f(9))$ e. Encontre esses valores$c$ garantidos pelo Teorema do Valor Médio.

Solução

Sabemos que$f(x)=\sqrt{x}$ é contínuo$[0,9]$ e diferenciável sobre$(0,9).$ Portanto,$f$ satisfaz as hipóteses do Teorema do Valor Médio, e deve existir pelo menos um valor$c∈(0,9)$ que$f′(c)$ seja igual à inclinação da linha que conecta$(0,f(0))$ e$(9,f(9))$ (Figura$\PageIndex{7}$). Para determinar quais valores de$c$ são garantidos, primeiro calcule a derivada de$f$. O derivado$f′(x)=\frac{1}{(2\sqrt{x})}$. A inclinação da linha que conecta$(0,f(0))$ e$(9,f(9))$ é dada por

\[\frac{f(9)−f(0)}{9−0}=\frac{\sqrt{9}−\sqrt{0}}{9−0}=\frac{3}{9}=\frac{1}{3}. \nonumber \]

Queremos encontrar$c$ isso$f′(c)=\frac{1}{3}$. Ou seja, queremos descobrir$c$ que

\[\frac{1}{2\sqrt{c}}=\frac{1}{3}. \nonumber \]

Resolvendo essa equação para$c$, obtemos$c=\frac{9}{4}$. Nesse ponto, a inclinação da reta tangente é igual à inclinação da linha que une as extremidades.

A função f (x) = a raiz quadrada de x é representada graficamente de (0, 0) a (9, 3). Há uma linha secante desenhada de (0, 0) a (9, 3). No ponto (9/4, 3/2), há uma linha tangente que é desenhada e essa linha é paralela à linha secante. — Figura$\PageIndex{7}$: A inclinação da reta tangente em$c=9/4$ é igual à inclinação do segmento de reta conectando (0,0) e (9,3).

Uma aplicação que ajuda a ilustrar o Teorema do Valor Médio envolve a velocidade. Por exemplo, suponha que dirigimos um carro por 1 h em uma estrada reta com uma velocidade média de 45 mph. Deixe$s(t)$ e$v(t)$ denote a posição e a velocidade do carro, respectivamente, para$0≤t≤1$ h. Supondo que a função de posição$s(t)$ seja diferenciável, podemos aplicar o Teorema do Valor Médio para concluir que, em algum momento$c∈(0,1)$, a velocidade do carro era exatamente

\[v(c)=s′(c)=\frac{s(1)−s(0)}{1−0}=45\,\text{mph.} \nonumber \]

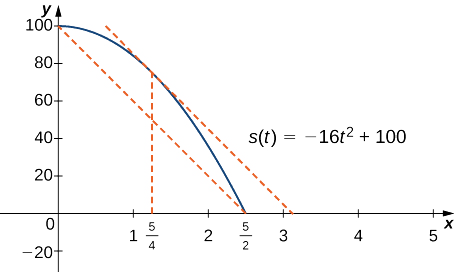
Exemplo$\PageIndex{3}$: Mean Value Theorem and Velocity

Se uma rocha cair de uma altura de 100 pés, sua posição$t$ segundos depois de cair até atingir o solo é dada pela função$s(t)=−16t^2+100.$

Determine quanto tempo leva até que a rocha atinja o solo.
Encontre a velocidade média$v_{avg}$ da rocha para quando a rocha é lançada e a rocha atinge o solo.
Encontre o tempo$t$ garantido pelo Teorema do Valor Médio quando a velocidade instantânea da rocha é$v_{avg}.$

Solução

a. Quando a rocha atinge o solo, sua posição é$s(t)=0$. Resolvendo a equação$−16t^2+100=0$ para$t$, descobrimos isso$t=±\frac{5}{2}sec$. Como estamos apenas considerando$t≥0$, a bola atingirá o chão$\frac{5}{2}$ segundos depois de cair.

b. A velocidade média é dada por

\[v_{avg}=\frac{s(5/2)−s(0)}{5/2−0}=\frac{0−100}{5/2}=−40\,\text{ft/sec}. \nonumber \]

c. A velocidade instantânea é dada pela derivada da função de posição. Portanto, precisamos encontrar um tempo$t$ como$v(t)=s′(t)=v_{avg}=−40$ pés/seg. Como$s(t)$ é contínuo ao longo do intervalo$[0,5/2]$ e diferenciável ao longo do intervalo$(0,5/2),$ pelo Teorema do Valor Médio, é garantido que haja um ponto$c∈(0,5/2)$ tal que

\[s′(c)=\frac{s(5/2)−s(0)}{5/2−0}=−40. \nonumber \]

Tomando a derivada da função de posição$s(t)$, descobrimos que$s′(t)=−32t.$ Portanto, a equação se reduz a$s′(c)=−32c=−40.$ Resolvendo esta equação para$c$, temos$c=\frac{5}{4}$. Portanto,$\frac{5}{4}$ segundos após a queda da rocha, a velocidade instantânea é igual à velocidade média da rocha durante sua queda livre:$−40$ pés/seg.

A função s (t) = −16t2 + 100 é representada graficamente de (0, 100) a (5/2, 0). Há uma linha secante desenhada de (0, 100) a (5/2, 0). No ponto correspondente a x = 5/4, há uma linha tangente que é desenhada e essa linha é paralela à linha secante. — Figura$\PageIndex{8}$: No tempo$t=5/4$ seg, a velocidade da rocha é igual à sua velocidade média desde o momento em que ela cai até atingir o solo.

Exercício$\PageIndex{2}$

Suponha que uma bola caia de uma altura de 200 pés. Sua posição no momento$t$ é$s(t)=−16t^2+200.$ Encontre o$t$ momento em que a velocidade instantânea da bola é igual à sua velocidade média.

Dica: Primeiro, determine quanto tempo a bola leva para atingir o chão. Em seguida, determine a velocidade média da bola desde o momento em que ela cai até atingir o chão.

Resposta: $\frac{5}{2\sqrt{2}}$seg

Corolários do Teorema do Valor Médio

Vamos agora ver três corolários do Teorema do Valor Médio. Esses resultados têm consequências importantes, que usaremos nas próximas seções.

Neste ponto, sabemos que a derivada de qualquer função constante é zero. O Teorema do Valor Médio nos permite concluir que o inverso também é verdadeiro. Em particular, se for$f′(x)=0$ para todos$x$ em algum intervalo$I$, então$f(x)$ é constante nesse intervalo. Esse resultado pode parecer intuitivamente óbvio, mas tem implicações importantes que não são óbvias, e as discutiremos em breve.

Corolário 1: Funções com uma derivada de zero

$f$Seja diferenciável em um intervalo$I$. Se for$f′(x)=0$ para todos$x∈I$, então$f(x)=$ constante para todos$x∈I.$

Prova

Uma vez que$f$ é diferenciável$I$,$f$ deve ser contínuo$I$. Suponha que não$f(x)$ seja constante para todos$x$$I$. Então existe$a,b∈I$, onde$a≠b$ e$f(a)≠f(b).$ escolha a notação para que$a<b.$ Portanto,

\[\frac{f(b)−f(a)}{b−a}≠0. \nonumber \]

Como$f$ é uma função diferenciável, pelo Teorema do Valor Médio, existe$c∈(a,b)$ tal que

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Portanto, existe$c∈I$ tal coisa$f′(c)≠0$, o que contradiz a suposição de que$f′(x)=0$ para todos$x∈I$.

□

De “Corolário 1: Funções com uma derivada de zero”, conclui-se que se duas funções têm a mesma derivada, elas diferem em, no máximo, uma constante.

Corolário 2: Teorema da diferença constante

Se$f$ e$g$ são diferenciáveis em um intervalo$I$ e$f′(x)=g′(x)$ para todos$x∈I$, então$f(x)=g(x)+C$ para alguma constante$C$.

Prova

Let$h(x)=f(x)−g(x).$ Then,$h′(x)=f′(x)−g′(x)=0$ para todos$x∈I.$ Por Corolário 1, existe uma constante$C$ tal que$h(x)=C$ para todos$x∈I$. Portanto,$f(x)=g(x)+C$ para todos$x∈I.$

□

O terceiro corolário do Teorema do Valor Médio discute quando uma função está aumentando e quando está diminuindo. Lembre-se de que uma função$f$ está aumentando$I$ se$f(x_1)<f(x_2)$ sempre$x_1<x_2$, enquanto$f$ está diminuindo sobre$I$ se$f(x_1)>f(x_2)$ sempre$x_1<x_2$. Usando o Teorema do Valor Médio, podemos mostrar que se a derivada de uma função for positiva, a função está aumentando; se a derivada for negativa, a função está diminuindo (Figura$\PageIndex{9}$). Usamos esse fato na próxima seção, onde mostramos como usar a derivada de uma função para localizar valores locais máximos e mínimos da função e como determinar a forma do gráfico.

Esse fato é importante porque significa que, para uma determinada função$f$, se existe uma função$F$ tal$F′(x)=f(x)$; então, as únicas outras funções que têm uma derivada igual a$f$ são$F(x)+C$ para alguma constante$C$. Discutiremos esse resultado com mais detalhes posteriormente neste capítulo.

Uma função vagamente sinusoidal f (x) é representada graficamente. Ele aumenta de algum lugar no segundo quadrante para (a, f (a)). Nesta seção, observa-se que f' — Figura$\PageIndex{9}$: Se uma função tiver uma derivada positiva em algum intervalo$I$, a função aumentará nesse intervalo$I$; se a derivada for negativa em algum intervalo$I$, a função diminuirá nesse intervalo$I$.

Corolário 3: funções crescentes e decrescentes

$f$Seja contínuo no intervalo fechado$[a,b]$ e diferenciável no intervalo aberto$(a,b)$.

Se for$f′(x)>0$ para todos$x∈(a,b)$, então$f$ uma função crescente acabou$[a,b].$
Se for$f′(x)<0$ para todos$x∈(a,b)$, então$f$ uma função decrescente acabou$[a,b].$

Prova

Vamos provar i.; a prova de ii. é similar. Suponha que não$f$ haja uma função crescente ativada$I$. Então existe$a$ e$b$ em$I$ tal coisa$a<b$, mas$f(a)≥f(b)$. Uma vez$f$ que uma função diferenciável acabou$I$, pelo Teorema do Valor Médio$c∈(a,b)$, existe tal que

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Desde então$f(a)≥f(b)$, sabemos disso$f(b)−f(a)≤0$. Além disso, nos$a<b$ diz que$b−a>0.$ concluímos que

\[f′(c)=\frac{f(b)−f(a)}{b−a}≤0. \nonumber \]

No entanto,$f′(x)>0$ para todos$x∈I$. Isso é uma contradição e, portanto,$f$ deve ser uma função crescente$I$.

□

Conceitos chave

Se$f$ é contínuo$[a,b]$ e diferenciável sobre$(a,b)$ e$f(a)=f(b)$, então existe um ponto$c∈(a,b)$ tal que$f′(c)=0.$ Este é o teorema de Rolle.
Se$f$ é contínuo$[a,b]$ e diferenciável sobre$(a,b)$, então existe um ponto$c∈(a,b)$ tal que\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \] Este é o Teorema do Valor Médio.
Se$f'(x)=0$ ao longo de um intervalo$I$, então$f$ é constante$I$.
Se duas funções diferenciáveis$f$ e$g$ satisfizerem$f′(x)=g′(x)$$I$, então$f(x)=g(x)+C$ para alguma constante$C$.
Se$f′(x)>0$ em um intervalo$I$, então$f$ está aumentando$I$. Se$f′(x)<0$ terminar$I$, então$f$ está diminuindo mais$I$.

Glossário

teorema do valor médio: se$f$ é contínuo$[a,b]$ e diferenciável$(a,b)$, então existe$c∈(a,b)$ tal que$f′(c)=\frac{f(b)−f(a)}{b−a}$

teorema de Rolle: se$f$ é contínuo$[a,b]$ e diferenciável sobre$(a,b)$, e se$f(a)=f(b)$, então existe$c∈(a,b)$ tal que$f′(c)=0$