4.3E: Exercícios para a Seção 4.3

Last updated
Save as PDF

Page ID: 188284

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) No pré-cálculo, você aprendeu uma fórmula para a posição do máximo ou mínimo de uma equação quadrática$y=ax^2+bx+c$, que era$m=−\frac{b}{2a}$. Prove essa fórmula usando cálculo.

2) Se você está encontrando um mínimo absoluto em um intervalo,$[a,b],$ por que precisa verificar os pontos finais? Desenhe um gráfico que suporte sua hipótese.

Responda: Em um intervalo fechado, os pontos finais geralmente estão acima ou abaixo de qualquer extremidade local (relativa). As respostas podem variar para o gráfico.

3) Se você estiver examinando uma função em um intervalo$(a,b),$ para$a$ e$b$ finito, é possível não ter um máximo absoluto ou um mínimo absoluto?

4) Ao verificar pontos críticos para localizar a extremidade de uma função$f$, explique por que você também precisa determinar pontos onde$f'(x)$ está indefinido. Desenhe um gráfico para apoiar sua explicação.

Responda: Os pontos no gráfico de$f$ onde há um canto, uma cúspide ou uma descontinuidade de salto ou descontinuidade removível podem facilmente ser a extremidade absoluta (ou local) da função. As respostas podem variar para o gráfico.

5) Você pode ter um máximo absoluto finito para$y=ax^2+bx+c$ mais de$(−∞,∞)$? Explique por que ou por que não usar argumentos gráficos.

6) Você pode ter um máximo absoluto finito para$y=ax^3+bx^2+cx+d$$(−∞,∞)$ assumir que$a$ é diferente de zero? Explique por que ou por que não usar argumentos gráficos.

Responda: Não; as respostas podem variar

7)$m$ Seja o número de mínimos locais e$M$ seja o número de máximos locais. Você pode criar uma função onde$M>m+2$? Desenhe um gráfico para apoiar sua explicação.

8) É possível ter mais de um máximo absoluto? Use um argumento gráfico para provar sua hipótese.

Responda: Como o máximo absoluto é o valor da função (saída) em vez do valor x, a resposta é não; as respostas variam

9) É possível não ter um mínimo ou máximo absoluto para uma função? Em caso afirmativo, construa essa função. Caso contrário, explique por que isso não é possível.

10) [T] Representa graficamente a função$y=e^{ax}.$ Para quais valores de$a$, em qualquer domínio infinito, você terá um mínimo absoluto e um máximo absoluto?

Responda: Quando$a=0$

Nos exercícios 11 a 14, determine onde os máximos e mínimos locais e absolutos ocorrem no gráfico fornecido. Suponha que os domínios sejam intervalos fechados, salvo indicação em contrário.

11)

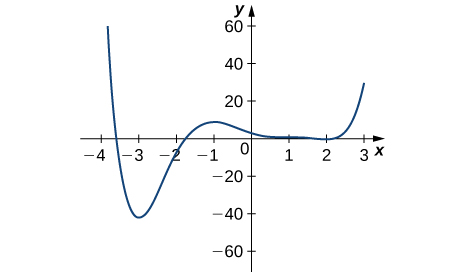
$A função representada graficamente começa em (−4, 60), diminui rapidamente para (−3, −40), aumenta para (−1, 10) antes de diminuir lentamente para (2, 0), momento em que aumenta rapidamente para (3, 30).$

12)

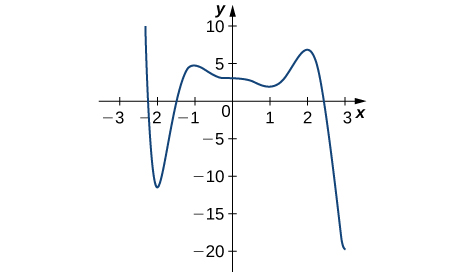
$A função representada graficamente começa em (−2,2, 10), diminui rapidamente para (−2, −11), aumenta para (−1, 5) antes de diminuir lentamente para (1, 3), momento em que aumenta para (2, 7) e depois diminui para (3, −20).$

Responda: Mínimo absoluto em 3; máximo absoluto em −2,2; mínimos locais em −2, 1; máximos locais em −1, 2

13)

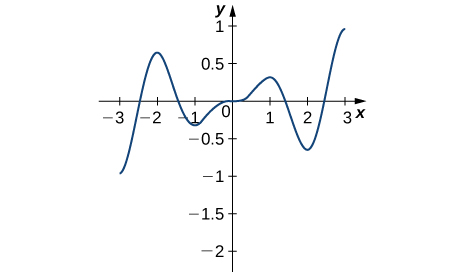
$A função representada graficamente começa em (−3, −1), aumenta rapidamente para (−2, 0,7), diminui para (−1, −0,25) antes de diminuir lentamente para (1, 0,25), momento em que diminui para (2, 0,7) e depois aumenta para (3, 1).$

14)

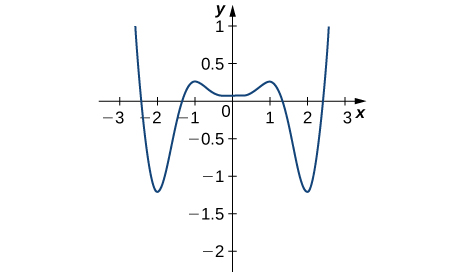
$A função representada graficamente começa em (−2,5, 1), diminui rapidamente para (−2, −1,25), aumenta para (−1, 0,25) antes de diminuir lentamente para (0, 0,2), momento em que aumenta lentamente para (1, 0,25), depois diminui rapidamente para (2, −1,25) e, finalmente, aumenta para (2,5, 1).$

Responda: Mínimos absolutos em −2, 2; máximos absolutos em −2,5, 2,5; mínimo local em 0; máximos locais em −1, 1

Para os exercícios 15 a 18, desenhe gráficos de$f(x)$, que são contínuos, ao longo do intervalo$[−4,4]$ com as seguintes propriedades:

15) Máximo absoluto em$x=2$ e mínimos absolutos em$x=±3$

16) Mínimo absoluto em$x=1$ e máximo absoluto em$x=2$

Responda: As respostas podem variar.

17) Máximo$x=4,$ absoluto no mínimo absoluto no máximo$x=−1,$ local em$x=−2,$ e um ponto crítico que não seja máximo ou mínimo em$x=2$

18) Máximos absolutos em$x=2$ e$x=−3$, mínimo local em$x=1$ e mínimo absoluto em$x=4$

Responda: As respostas podem variar.

Nos exercícios 19 a 28, encontre os pontos críticos nos domínios das funções dadas.

19)$y=4x^3−3x$

20)$y=4\sqrt{x}−x^2$

Responda: $x=1$

21)$y=\dfrac{1}{x−1}$

22)$y=\ln(x−2)$

Responda: Nenhuma

23)$y=\tan(x)$

24)$y=\sqrt{4−x^2}$

Responda: $x=0$

25)$y=x^{3/2}−3x^{5/2}$

26)$y=\dfrac{x^2−1}{x^2+2x−3}$

Responda: Nenhuma

27)$y=\sin^2(x)$

28)$y=x+\dfrac{1}{x}$

Responda: $x=−1$e$x = 1$

Nos exercícios 29 a 39, encontre os máximos locais e/ou absolutos para as funções no domínio especificado.

29)$f(x)=x^2+3$ acabou$[−1,4]$

30)$y=x^2+\dfrac{2}{x}$ mais$[1,4]$

Responda: Máximo absoluto$x=4, y=\frac{33}{2}$; mínimo absoluto:$x=1, y=3$

31)$y=(x−x^2)^2$ acabou$[−1,1]$

32)$y=\dfrac{1}{x−x^2}$ mais$[0,1]$

Responda: mínimo absoluto:$x=\frac{1}{2}, y=4$

33)$y=\sqrt{9−x}$ acabou$[1,9]$

34)$y=x+\sin(x)$ acabou$[0,2π]$

Responda: máximo absoluto: mínimo$x=2π, y=2π;$ absoluto:$x=0, y=0$

35)$y=\dfrac{x}{1+x}$ mais$[0,100]$

36)$y=|x+1|+|x−1|$ acabou$[−3,2]$

Responda: máximo absoluto: mínimo$x=−3, y = 6;$ absoluto:$−1≤x≤1, y=2$

37)$y=\sqrt{x}−\sqrt{x^3}$ mais$[0,4]$

38)$y=\sin x+\cos x$ mais$[0,2π]$

Resposta: Máximo absoluto$x=\frac{π}{4}, y=\sqrt{2}$; mínimo absoluto:$x=\frac{5π}{4}, y=−\sqrt{2}$

39)$y=4\sin θ−3\cos θ$ acabou$[0,2π]$

Nos exercícios 40 a 45, determine os mínimos e máximos locais e absolutos para as funções acima$(−∞,∞).$

40)$y=x^2+4x+5$

Resposta: mínimo absoluto:$x=−2, y=1$

41)$y=x^3−12x$

(42)$y=3x^4+8x^3−18x^2$

Resposta: Mínimo absoluto: máximo$x=−3, y=−135;$ local:$x=0, y=0$; mínimo local:$x=1, y=−7$

43)$y=x^3(1−x)^6$

44)$y=\dfrac{x^2+x+6}{x−1}$

Resposta: Máximo local:$x=1−2\sqrt{2}, y=3−4\sqrt{2}$; mínimo local:$x=1+2\sqrt{2}, y=3+4\sqrt{2}$

45)$y=\dfrac{x^2−1}{x−1}$

Nos exercícios 46 a 50, use uma calculadora para representar graficamente a função e estimar os máximos e mínimos absolutos e locais. Em seguida, resolva-os explicitamente.

46) [T]$y=3x\sqrt{1−x^2}$

Resposta: máximo absoluto: mínimo$x=\frac{\sqrt{2}}{2}, y=\frac{3}{2};$ absoluto:$x=−\frac{\sqrt{2}}{2}, y=−\frac{3}{2}$

47) [T]$y=x+\sin(x)$

48) [T]$y=12x^5+45x^4+20x^3−90x^2−120x+3$

Resposta: Máximo local:$x=−2,y=59$; mínimo local:$x=1, y=−130$

49) [T]$y=\dfrac{x^3+6x^2−x−30}{x−2}$

50) [T]$y=\dfrac{\sqrt{4−x^2}}{\sqrt{4+x^2}}$

Resposta: máximo absoluto: mínimo$x=0, y=1;$ absoluto:$x=−2,2, y=0$

51) Uma empresa que produz telefones celulares tem uma função de custo de$C=x^2−1200x+36,400,$ onde$C$ é o custo em dólares e$x$ é o número de telefones celulares produzidos (em milhares). Quantas unidades de celular (em milhares) minimizam essa função de custo?

52) Uma bola é lançada no ar e sua posição é dada por$h(t)=−4.9t^2+60t+5m.$ Encontre a altura na qual a bola para de subir. Quanto tempo depois de ser lançado isso acontece?

Resposta: $h=\frac{9245}{49}$ms$t=\frac{300}{49}$,

Para os exercícios 53-54, considere a produção de ouro durante a corrida do ouro na Califórnia (1848—1888). A produção de ouro pode ser modelada por$G(t)=\dfrac{(25t)}{(t^2+16)}$, onde$t$ está o número de anos desde o início da correria$(0≤t≤40)$ e$G$ são onças de ouro produzidas (em milhões). Um resumo dos dados é mostrado na figura a seguir.

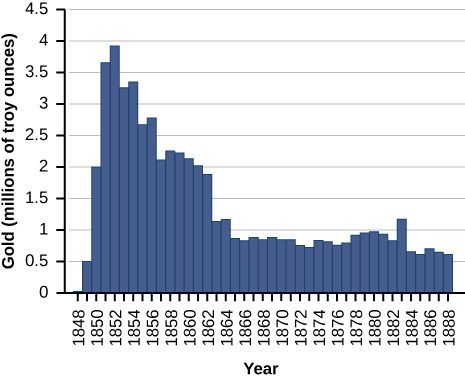
$O gráfico de barras mostra ouro (em milhões de onças troy) por ano, começando em 1848 e terminando em 1888. Em 1848, o gráfico de barras mostra 0,05; em 1849, 0,5; em 1850, 2; em 1851, 3,6; em 1852, 3,9; em 1853, 3,3; em 1854, 3,4; em 1855, 2,6; em 1856, 2,75; em 1857, 2,1; em 1858, 2,2; em 1859, 2,15; em 1860, 2,1; em 1861, 2; em 1862, 1,8; em 1863, 1,1; em 1864, 1,15; em 1865, 0,9; em 1866, 0,85; em 1867, 0,9; em 1868, 0,85 ; em 1869, 0,9; em 1870, 0,85; em 1871, 0,85; em 1872, 0,75; em 1873, 0,7; em 1874, 0,8; em 1875, 0,75; em 1876, 0,7; em 1877, 0,73; em 1878, 0,9; em 1879, 0,95; em 1880, 1; em 1881, 0,95; em 1882, 0,85; em 1880, 1; em 1881, 0,95; em 1882, 0,85; em 1880 83, 1,1; em 1884, 0,6; em 1885, 0,55; em 1886, 0,65; em 1887, 0,6; e em 1888, 0,55.$

53) Descubra quando ocorreu a produção máxima (local e global) de ouro e a quantidade de ouro produzida durante esse máximo.

54) Descubra quando ocorreu a produção mínima (local e global) de ouro. Qual foi a quantidade de ouro produzida durante esse mínimo?

Resposta: O mínimo global foi em 1848, quando nenhum ouro foi produzido.

Nos exercícios 55 e 56, encontre os pontos críticos, máximos e mínimos para determinadas funções por partes.

55)$y= \begin{cases} x^2−4x, & \text{if }0≤x≤1\\x^2−4, & \text{if }1<x≤2 \end{cases}$

(56)$y=\begin{cases}x^2+1, & \text{if }x≤1 \\ x^2−4x+5, & \text{if }x>1\end{cases}$

Resposta: Mínimos absolutos:$x=0, x=2, y=1$; máximo local em$x=1, y=2$

Nos exercícios 57 a 58, encontre os pontos críticos das seguintes funções genéricas. Eles são máximos, mínimos ou nenhum deles? Indique as condições necessárias.

57)$y=ax^2+bx+c,$ dado que$a>0$

58)$y=(x−1)^a$, dado que$a>1$

Resposta: Sem máximo/mínimo se$a$ for ímpar, mínimo em$x=1$ se$a$ for par

Contribuidores e atribuições

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added answers for exercises 2 and 4.