4.3: Máxima e Mínima

Last updated
Save as PDF

Page ID: 188271

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Defina extrema absoluta.
Defina os extremos locais.
Explique como encontrar os pontos críticos de uma função em um intervalo fechado.
Descreva como usar pontos críticos para localizar extremos absolutos em um intervalo fechado.

Dada uma função específica, geralmente estamos interessados em determinar os maiores e menores valores da função. Essas informações são importantes na criação de gráficos precisos. Encontrar os valores máximo e mínimo de uma função também tem significado prático, pois podemos usar esse método para resolver problemas de otimização, como maximizar o lucro, minimizar a quantidade de material usado na fabricação de uma lata de alumínio ou encontrar a altura máxima que um foguete pode alcançar. Nesta seção, veremos como usar derivadas para encontrar os maiores e os menores valores de uma função.

Extrema absoluta

Considere a função\(f(x)=x^2+1\) ao longo do intervalo\((−∞,∞)\). Como\(x→±∞, f(x)→∞\). Portanto, a função não tem um valor maior. No entanto, como\(x^2+1≥1\) para todos os números reais\(x\) e\(x^2+1=1\) quando\(x=0\), a função tem um valor menor,\(1\), quando\(x=0\). Dizemos que\(1\) é o mínimo absoluto de\(f(x)=x^2+1\) e ocorre em\(x=0\). Dizemos que\(f(x)=x^2+1\) não tem um máximo absoluto (Figura\(\PageIndex{1}\)).

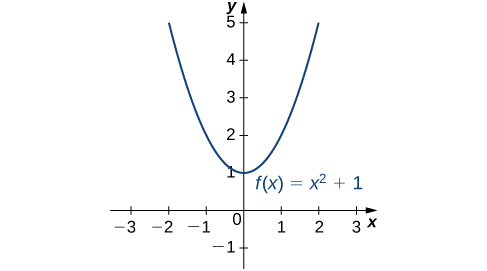
A função f (x) = x^2 + 1 é representada graficamente e seu mínimo de 1 é visto em x = 0. — Figura\(\PageIndex{1}\): A função dada tem um mínimo absoluto de\(1\) at\(x=0\). A função não tem um máximo absoluto.

Definição: Extrema absoluta

\(f\)Seja uma função definida em um intervalo\(I\) e deixe\(c∈I\). Dizemos que\(f\) tem um máximo absoluto de\(I\) at\(c\) if\(f(c)≥f(x)\) for all\(x∈I\). Dizemos que\(f\) tem um mínimo absoluto de\(I\) at\(c\) if\(f(c)≤f(x)\) for all\(x∈I\). Se\(f\) tem um máximo absoluto em\(I\) at\(c\) ou um mínimo absoluto em\(I\) at\(c\), dizemos que\(f\) tem um extremo absoluto em\(I\) at\(c\).

Antes de prosseguir, vamos observar duas questões importantes relacionadas a essa definição. Primeiro, o termo absoluto aqui não se refere ao valor absoluto. Um extremo absoluto pode ser positivo, negativo ou zero. Segundo, se uma função\(f\) tem um extremo absoluto em um intervalo\(I\) em\(c\), o extremo absoluto é\(f(c)\). O número real\(c\) é um ponto no domínio em que ocorre o extremo absoluto. Por exemplo, considere a função\(f(x)=1/(x^2+1)\) ao longo do intervalo\((−∞,∞)\). Desde

\[f(0)=1≥\frac{1}{x^2+1}=f(x) \nonumber \]

para todos os números reais\(x\), dizemos que\(f\) tem um máximo absoluto acima de\((−∞,∞)\) em\(x=0\). O máximo absoluto é\(f(0)=1\). Ocorre em\(x=0\), conforme mostrado na Figura\(\PageIndex{2}\) (b).

Uma função pode ter um máximo absoluto e um mínimo absoluto, apenas um extremo ou nenhum dos dois. A figura\(\PageIndex{2}\) mostra várias funções e algumas das diferentes possibilidades em relação à extrema absoluta. No entanto, o seguinte teorema, chamado Teorema do Valor Extremo, garante que uma função\(f\) contínua em um intervalo fechado e limitado\([a,b]\) tenha tanto um máximo absoluto quanto um mínimo absoluto.

Esta figura tem seis partes a, b, c, d, e f. Na figura a, a linha f (x) = x^3 é mostrada, e nota-se que ela não tem mínimo absoluto nem máximo absoluto. Na figura b, a linha f (x) = 1/ (x^2 + 1) é mostrada, que está próxima de 0 na maior parte de seu comprimento e sobe para uma protuberância em (0, 1); ela não tem mínimo absoluto, mas tem um máximo absoluto de 1 em x = 0. Na figura c, a linha f (x) = cos x é mostrada, que tem mínimos absolutos de −1 em ±π, ±3π,... e máximos absolutos de 1 em 0, ±2π, ±4π,... Na figura d, a função por partes f (x) = 2 — x^2 para 0 ≤ x < 2 e x — 3 para 2 ≤ x ≤ 4 é mostrada, com máximo absoluto de 2 em x = 0 e sem mínimo absoluto. Na figura e, a função f (x) = (x — 2) 2 é mostrada em [1, 4], que tem máximo absoluto de 4 em x = 4 e mínimo absoluto de 0 em x = 2. Na figura f, a função f (x) = x/ (2 − x) é mostrada em [0, 2), com mínimo absoluto de 0 em x = 0 e sem máximo absoluto. — Figura\(\PageIndex{2}\): Os gráficos (a), (b) e (c) mostram várias possibilidades de extrema absoluta para funções com um domínio de\((−∞,∞).\) Os gráficos (d), (e) e (f) mostram várias possibilidades de extrema absoluta para funções com um domínio que é um intervalo limitado.

Teorema\(\PageIndex{1}\): Extreme Value Theorem

Se\(f\) for uma função contínua sobre o intervalo fechado e limitado\([a,b]\), então há um ponto\([a,b]\) no qual\(f\) tem um máximo absoluto acima\([a,b]\) e há um ponto\([a,b]\) no qual\(f\) tem um mínimo absoluto acima\([a,b]\).

A prova do teorema do valor extremo está além do escopo deste texto. Normalmente, isso é comprovado em um curso sobre análise real. Há alguns pontos-chave a serem observados sobre a afirmação desse teorema. Para que o teorema do valor extremo seja aplicado, a função deve ser contínua em um intervalo fechado e limitado. Se o intervalo\(I\) estiver aberto ou a função tiver pelo menos um ponto de descontinuidade, a função pode não ter um máximo absoluto ou um mínimo absoluto acima\(I\). Por exemplo, considere as funções mostradas na Figura\(\PageIndex{2}\) (d), (e) e (f). Todas essas três funções são definidas em intervalos limitados. No entanto, a função no gráfico (e) é a única que tem um máximo absoluto e um mínimo absoluto sobre seu domínio. O teorema do valor extremo não pode ser aplicado às funções nos gráficos (d) e (f) porque nenhuma dessas funções é contínua em um intervalo fechado e limitado. Embora a função no gráfico (d) seja definida no intervalo fechado\([0,4]\), a função é descontínua em\(x=2\). A função tem um máximo absoluto acima\([0,4]\), mas não tem um mínimo absoluto. A função no gráfico (f) é contínua no intervalo semiaberto\([0,2)\), mas não está definida em e\(x=2\), portanto, não é contínua em um intervalo fechado e limitado. A função tem um mínimo absoluto acima\([0,2)\), mas não tem um máximo absoluto acima\([0,2)\). Esses dois gráficos ilustram por que uma função em um intervalo limitado pode deixar de ter um máximo absoluto e/ou mínimo absoluto.

Antes de ver como encontrar a extrema absoluta, vamos examinar o conceito relacionado de extrema local. Essa ideia é útil para determinar onde ocorrem os extremos absolutos.

Pontos extremos e críticos locais

Considere a função\(f\) mostrada na Figura\(\PageIndex{3}\). O gráfico pode ser descrito como duas montanhas com um vale no meio. O valor máximo absoluto da função ocorre no pico mais alto, em\(x=2\). No entanto, também\(x=0\) é um ponto de interesse. Embora não\(f(0)\) seja o maior valor de\(f\), o valor\(f(0)\) é maior do que\(f(x)\) para todos\(x\) próximos de 0. Dizemos que\(f\) tem um máximo local em\(x=0\). Da mesma forma, a função\(f\) não tem um mínimo absoluto, mas tem um mínimo local em\(x=1\) porque\(f(1)\) é menor do que\(f(x)\) para\(x\) perto de 1.

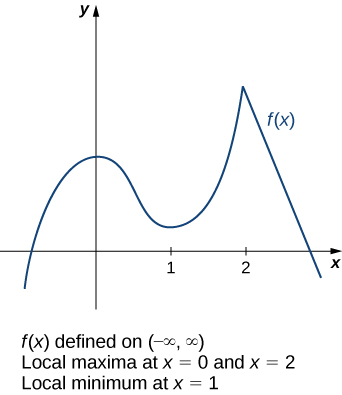
A função f (x) é mostrada, que se curva para cima a partir do quadrante III, diminui a velocidade no quadrante II, atinge um máximo local no eixo y, diminui para atingir um mínimo local no quadrante I em x = 1, aumenta para um máximo local em x = 2 que é maior do que o outro máximo local e, em seguida, diminui rapidamente quadrante IV. — Figura\(\PageIndex{3}\): Essa função\(f\) tem dois máximos locais e um mínimo local. O máximo local em também\(x=2\) é o máximo absoluto.

Definição: Local Extrema

Uma função\(f\) tem um máximo local em\(c\) se existir um intervalo aberto\(I\) contendo\(c\) um que\(I\) esteja contido no domínio de\(f\) e\(f(c)≥f(x)\) para todos\(x∈I\). Uma função\(f\) tem um mínimo local em\(c\) se existir um intervalo aberto\(I\) contendo\(c\) um que\(I\) esteja contido no domínio de\(f\) e\(f(c)≤f(x)\) para todos\(x∈I\). Uma função\(f\) tem um extremo local em\(c\) se\(f\) tem um máximo local em\(c\) ou\(f\) tem um mínimo local em\(c\).

Observe que se\(f\) tem um extremo absoluto em\(c\) e\(f\) é definido em um intervalo contendo\(c\), então também\(f(c)\) é considerado um extremo local. Se um extremo absoluto para uma função\(f\) ocorre em um ponto final, não consideramos que seja um extremo local, mas nos referimos a isso como um extremo final.

Dado o gráfico de uma função\(f\), às vezes é fácil ver onde ocorre um máximo local ou mínimo local. No entanto, nem sempre é fácil de ver, pois os recursos interessantes no gráfico de uma função podem não ser visíveis porque ocorrem em uma escala muito pequena. Além disso, podemos não ter um gráfico da função. Nesses casos, como podemos usar uma fórmula para uma função para determinar onde esses extremos ocorrem?

Para responder a essa pergunta, vamos dar uma olhada na Figura\(\PageIndex{3}\) novamente. Os extremos locais ocorrem em\(x=0, x=1,\) e\(x=2.\) Observe que em\(x=0\) e\(x=1\), a derivada\(f'(x)=0\). Em\(x=2\), a derivada\(f'(x)\) não existe, pois a função\(f\) tem um canto ali. Na verdade, se\(f\) tiver um extremo local em um ponto\(x=c\), a derivada\(f'(c)\) deve satisfazer uma das seguintes condições:\(f'(c)=0\) ou\(f'(c)\) é indefinida. Esse valor\(c\) é conhecido como ponto crítico e é importante para encontrar valores extremos para funções.

Definição: Pontos críticos

\(c\)Seja um ponto interior no domínio de\(f\). Dizemos que esse\(c\) é um ponto crítico de\(f\) se\(f'(c)=0\) ou\(f'(c)\) é indefinido.

Como mencionado anteriormente, se\(f\) tem um extremo local em um ponto\(x=c\), então\(c\) deve ser um ponto crítico de\(f\). Esse fato é conhecido como teorema de Fermat.

Teorema\(\PageIndex{2}\): Fermat’s Theorem

Se\(f\) tem um extremo local em\(c\) e\(f\) é diferenciável em\(c\), então\(f'(c)=0.\)

Prova

Suponha que\(f\) tenha uma extremidade local em\(c\) e\(f\) seja diferenciável em\(c\). Precisamos mostrar isso\(f'(c)=0\). Para fazer isso, mostraremos isso\(f'(c)≥0\) e\(f'(c)≤0\), portanto\(f'(c)=0\). Uma vez que\(f\) tem um extremo local em\(c\),\(f\) tem um máximo local ou mínimo local em\(c\). Suponha que\(f\) tenha um máximo local em\(c\). O caso em que\(f\) tem um mínimo local em\(c\) pode ser tratado de forma semelhante. Existe então um intervalo aberto I tal que\(f(c)≥f(x)\) para todos\(x∈I\). Como\(f\) é diferenciável em\(c\), a partir da definição da derivada, sabemos que

\[f'(c)=\lim_{x→c}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Como esse limite existe, os dois limites unilaterais também existem e são iguais\(f'(c)\). Portanto,

\[f'(c)=\lim_{x→c^+}\frac{f(x)−f(c)}{x−c,}\label{FermatEqn2} \]

\[f'(c)=\lim_{x→c^−}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Como\(f(c)\) é um máximo local, vemos isso\(f(x)−f(c)≤0\) por\(x\) perto\(c\). Portanto, por\(x\) quase\(c\), mas\(x>c\), nós temos\(\frac{f(x)−f(c)}{x−c}≤0\). A partir da Equação\ ref {FermateQN2} concluímos que\(f'(c)≤0\). Da mesma forma, pode-se mostrar que\(f'(c)≥0.\) Portanto,\(f'(c)=0.\)

□

A partir do teorema de Fermat, concluímos que se\(f\) tem um extremo local em\(c\), então\(f'(c)=0\) ou\(f'(c)\) é indefinido. Em outras palavras, a extrema local só pode ocorrer em pontos críticos.

Observe que este teorema não afirma que uma função\(f\) deve ter uma extremidade local em um ponto crítico. Em vez disso, afirma que os pontos críticos são candidatos aos extremos locais. Por exemplo, considere a função\(f(x)=x^3\). Nós temos\(f'(x)=3x^2=0\) quando\(x=0\). Portanto,\(x=0\) é um ponto crítico. No entanto,\(f(x)=x^3\) está aumentando e\((−∞,∞)\), portanto,\(f\) não tem um extremo local em\(x=0\). Na Figura\(\PageIndex{4}\), vemos várias possibilidades diferentes para pontos críticos. Em alguns desses casos, as funções têm extremos locais em pontos críticos, enquanto em outros casos as funções não. Observe que esses gráficos não mostram todas as possibilidades para o comportamento de uma função em um ponto crítico.

Esta figura tem cinco partes a, b, c, d e e. Na figura a, uma parábola é mostrada voltada para baixo no quadrante I; há uma linha tangente horizontal no máximo local marcada f' (c) = 0. Na figura b, há uma função desenhada com uma assíntota em c, o que significa que a função aumenta em direção ao infinito em ambos os lados de c; nota-se que f' (c) é indefinida. Na figura c, é mostrada uma versão do gráfico de valor absoluto que foi deslocada para que seu mínimo esteja no quadrante I com x = c. Observa-se que f' (c) é indefinido. Na figura d, é mostrada uma versão da função f (x) = x^3 que foi deslocada para que seu ponto de inflexão fique no quadrante I com x = c. Seu ponto de inflexão em (c, f (c)) tem uma linha horizontal através dela, e observa-se que f' (c) = 0. Na figura e, é mostrada uma versão da função f (x) = x1/3 que foi deslocada para que seu ponto de inflexão fique no quadrante I com x = c. Seu ponto de inflexão em (c, f (c)) tem uma linha vertical passando por ela, e observa-se que f' (c) é indefinido. — Figura\(\PageIndex{4}\): (a—e) Uma função\(f\) tem um ponto crítico em\(c\) se\(f'(c)=0\) ou\(f'(c)\) é indefinido. Uma função pode ou não ter um extremo local em um ponto crítico.

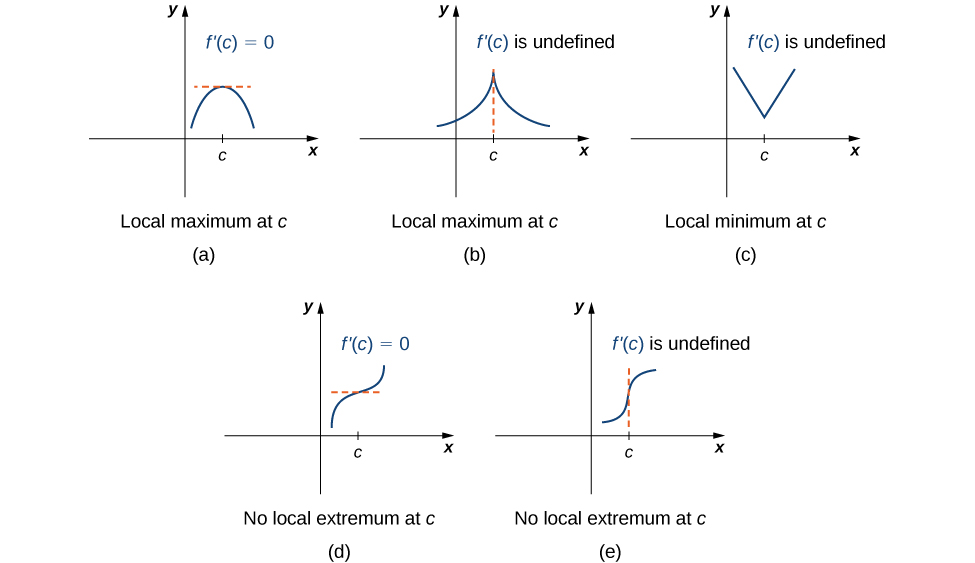
Mais adiante neste capítulo, examinaremos métodos analíticos para determinar se uma função realmente tem uma extremidade local em um ponto crítico. Por enquanto, vamos voltar nossa atenção para encontrar pontos críticos. Usaremos observações gráficas para determinar se um ponto crítico está associado a uma extremidade local.

Exemplo\(\PageIndex{1}\): Locating Critical Points

Para cada uma das funções a seguir, encontre todos os pontos críticos. Use um utilitário gráfico para determinar se a função tem um extremo local em cada um dos pontos críticos.

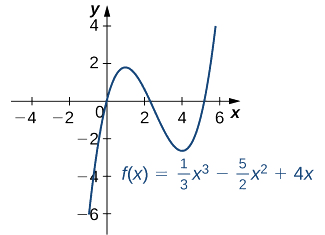
\(f(x)=\frac{1}{3}x^3−\frac{5}{2}x^2+4x\)
\(f(x)=(x^2−1)^3\)
\(f(x)=\frac{4x}{1+x^2}\)

Solução

a. A derivada\(f'(x)=x^2−5x+4\) é definida para todos os números reais\(x\). Portanto, só precisamos encontrar os valores para\(x\) onde\(f'(x)=0\). Uma vez que\(f'(x)=x^2−5x+4=(x−4)(x−1)\), os pontos críticos são\(x=1\) e A\(x=4.\) partir do gráfico da\(f\) Figura\(\PageIndex{5}\), vemos que\(f\) tem um máximo local em\(x=1\) e um mínimo local em\(x=4\).

A função f (x) = (1/3) x^3 — (5/2) x^2 + 4x é representada graficamente. A função tem máximo local em x = 1 e mínimo local em x = 4. — Figura\(\PageIndex{5}\): Essa função tem um máximo local e um mínimo local.

b. Usando a regra da cadeia, vemos que a derivada é

\(f'(x)=3(x^2−1)^2(2x)=6x(x^2−1)^2.\)

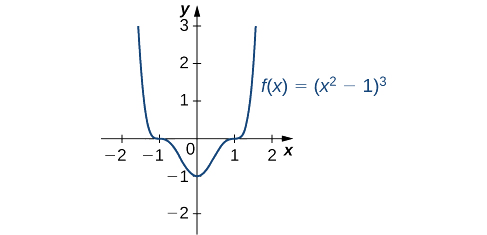
Portanto,\(f\) tem pontos críticos quando\(x=0\) e quando\(x^2−1=0\). Concluímos que os pontos críticos são\(x=0,±1\). A partir do gráfico da\(f\) Figura\(\PageIndex{6}\), vemos que\(f\) tem um mínimo local (e absoluto) em\(x=0\), mas não tem uma extremidade local em\(x=1\) ou\(x=−1\).

A função f (x) = (x^2 − 1) 3 é representada graficamente. A função tem mínimo local em x = 0 e pontos de inflexão em x = ±1. — Figura\(\PageIndex{6}\): Essa função tem três pontos críticos:\(x=0\)\(x=1\),\(x=−1\) e. A função tem um mínimo local (e absoluto) em\(x=0\), mas não tem extremos nos outros dois pontos críticos.

c. Pela regra do quociente, vemos que a derivada é

\(f'(x)=\frac{4(1+x^2)−4x(2x)}{(1+x^2)^2}=\frac{4−4x^2}{(1+x^2)^2}\).

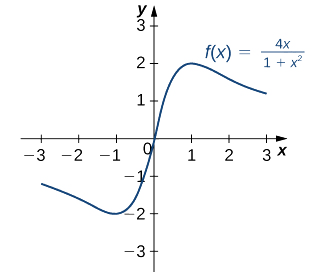
A derivada é definida em todos os lugares. Portanto, só precisamos encontrar valores para\(x\) onde\(f'(x)=0\). Resolvendo\(f'(x)=0\), vemos o\(4−4x^2=0,\) que implica\(x=±1\). Portanto, os pontos críticos são\(x=±1\). A partir do gráfico da\(f\) Figura\(\PageIndex{7}\), vemos que f tem um máximo absoluto em\(x=1\) e um mínimo absoluto em\(x=−1.\) Portanto,\(f\) tem um máximo local em\(x=1\) e um mínimo local em\(x=−1\). (Observe que se\(f\) tem um extremo absoluto em um intervalo\(I\) em um ponto\(c\) que não é um ponto final de\(I\), então\(f\) tem um extremo local em\(c.)\)

A função f (x) = 4x/ (1 + x^2) é representada graficamente. A função tem máximo local/absoluto em x = 1 e mínimo local/absoluto em x = −1. — Figura\(\PageIndex{7}\): Esta função tem um máximo absoluto e um mínimo absoluto.

Exercício\(\PageIndex{1}\)

Encontre todos os pontos críticos para\(f(x)=x^3−\frac{1}{2}x^2−2x+1.\)

Dica: Calcular\(f'(x).\)

Resposta: \(x=\frac{−2}{3}, x=1\)

Localizando a extrema absoluta

O teorema do valor extremo afirma que uma função contínua em um intervalo fechado e limitado tem um máximo absoluto e um mínimo absoluto. Conforme mostrado na Figura\(\PageIndex{2}\), um ou ambos os extremos absolutos podem ocorrer em um ponto final. No entanto, se um extremo absoluto não ocorrer em um ponto final, ele deve ocorrer em um ponto interno, caso em que o extremo absoluto é um extremo local. Portanto, pelo Teorema de Fermat, o ponto\(c\) em que a extremidade local ocorre deve ser um ponto crítico. Resumimos esse resultado no seguinte teorema.

Teorema\(\PageIndex{3}\): Location of Absolute Extrema

\(f\)Seja uma função contínua em um intervalo fechado e limitado\(I\). O máximo absoluto de\(f\) over\(I\) e o mínimo absoluto de\(f\) over\(I\) devem ocorrer nos pontos finais de\(I\) ou nos pontos críticos de\(f\) in\(I\).

Com essa ideia em mente, vamos examinar um procedimento para localizar extremos absolutos.

Estratégia de resolução de problemas: localização de extremos absolutos em um intervalo fechado

Considere uma função contínua\(f\) definida no intervalo fechado\([a,b].\)

\(f\)Avalie nos endpoints\(x=a\) e\(x=b.\)
Encontre todos os pontos críticos\(f\) dessa linha ao longo do intervalo\((a,b)\) e avalie\(f\) nesses pontos críticos.
Compare todos os valores encontrados em (1) e (2). A partir de “Localização da Extrema Absoluta”, a extrema absoluta deve ocorrer em pontos finais ou pontos críticos. Portanto, o maior desses valores é o máximo absoluto de\(f\). O menor desses valores é o mínimo absoluto de\(f\).

Agora, vamos ver como usar essa estratégia para encontrar os valores absolutos máximos e mínimos absolutos para funções contínuas.

Exemplo\(\PageIndex{2}\): Locating Absolute Extrema

Para cada uma das funções a seguir, encontre o máximo absoluto e o mínimo absoluto no intervalo especificado e indique onde esses valores ocorrem.

\(f(x)=−x^2+3x−2\)acabou\([1,3].\)
\(f(x)=x^2−3x^{2/3}\)acabou\([0,2]\).

Solução

a. Etapa 1. \(f\)Avalie nos endpoints\(x=1\)\(x=3\) e.

\(f(1)=0\)e\(f(3)=−2\)

Etapa 2. Como\(f'(x)=−2x+3, f'\) é definido para todos os números reais.\(x.\) Portanto, não há pontos críticos em que a derivada seja indefinida. Resta verificar onde\(f'(x)=0\). Uma vez que\(f'(x)=−2x+3=0 \) em\(x=\frac{3}{2}\) e\(\frac{3}{2}\) está no intervalo,\([1,3], f(\frac{3}{2})\) é candidato a um extremo absoluto de\(f\) mais\([1,3]\). Nós avaliamos\(f(\frac{3}{2})\) e encontramos

\(f\left(\frac{3}{2}\right)=\frac{1}{4}\).

Etapa 3. Configuramos a tabela a seguir para comparar os valores encontrados nas etapas 1 e 2.

\(x\)	\(f(x)\)	Conclusão
\(1\)	\(0\)
\(\frac{3}{2}\)	\(\frac{1}{4}\)	máximo absoluto
\(3\)	\(−2\)	mínimo absoluto

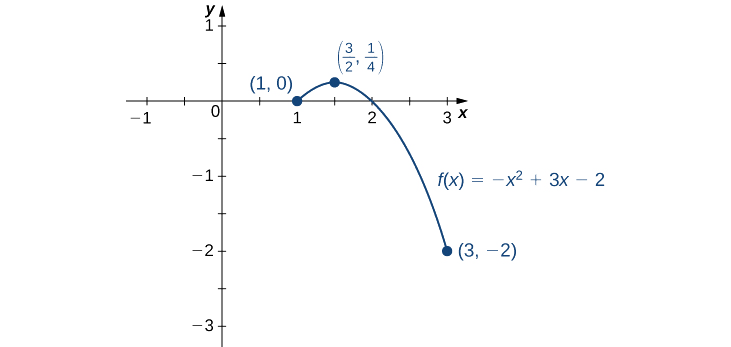
A partir da tabela, descobrimos que o máximo absoluto do intervalo [1, 3] é\(\frac{1}{4}\) e ocorre em\(x=\frac{3}{2}\).\(f\) O mínimo absoluto do intervalo\([1, 3]\) é\(−2\), e ocorre\(x=3\) conforme mostrado na Figura\(\PageIndex{8}\).\(f\)

A função f (x) = — x^2 + 3x — 2 é representada graficamente de (1, 0) a (3, −2), com seu máximo marcado em (3/2, 1/4). — Figura\(\PageIndex{8}\): Essa função tem um máximo absoluto e um mínimo absoluto.

b. Etapa 1. \(f\)Avalie nos endpoints\(x=0\)\(x=2\) e.

\(f(0)=0\)e\(f(2)=4−3\left(2\right)^{2/3}≈−0.762\)

Etapa 2. A derivada de\(f\) é dada por

\(f'(x)=2x−\frac{2}{x^{1/3}}=\dfrac{2x^{4/3}−2}{x^{1/3}}\)

para\(x≠0\). A derivada é zero quando\(2x^{4/3}−2=0\), o que implica\(x=±1\). A derivada é indefinida em\(x=0\). Portanto, os pontos críticos do\(f\) são\(x=0,1,−1\). O ponto\(x=0\) é um ponto final, então já avaliamos\(f(0)\) na etapa 1. O ponto não\(x=−1\) está no intervalo de interesse, então precisamos apenas avaliar\(f(1)\). Nós descobrimos que

\(f(1)=−2.\)

Etapa 3. Comparamos os valores encontrados nas etapas 1 e 2, na tabela a seguir.

\(x\)	\(f(x)\)	Conclusão
\(0\)	\(0\)	máximo absoluto
\(1\)	\(−2\)	mínimo absoluto
\(2\)	\(−0.762\)

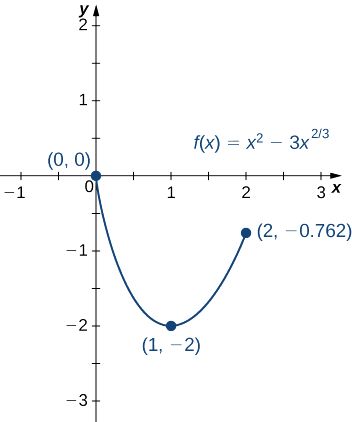
Concluímos que o máximo absoluto de\(f\) mais do que o intervalo\([0, 2]\) é zero e ocorre em\(x=0\). O mínimo absoluto é\(−2,\) e ocorre\(x=1\) conforme mostrado na Figura\(\PageIndex{9}\).

A função f (x) = x^2 — 3x^ (2/3) é representada graficamente de (0, 0) a (2, −0,762), com seu mínimo marcado em (1, −2). — Figura\(\PageIndex{9}\): Essa função tem um máximo absoluto em uma extremidade do intervalo.

Exercício\(\PageIndex{2}\)

Encontre o máximo absoluto e o mínimo absoluto de\(f(x)=x^2−4x+3\) ao longo do intervalo\([1,4]\).

Dica: Procure pontos críticos. Avalie\(f\) em todos os pontos críticos e nos pontos finais.

Resposta: O máximo absoluto é\(3\) e ocorre em\(x=4\). O mínimo absoluto é\(−1\) e ocorre em\(x=2\).

Neste ponto, sabemos como localizar extremos absolutos para funções contínuas em intervalos fechados. Também definimos a extremidade local e determinamos que, se uma função\(f\) tem uma extremidade local em um ponto\(c\), então\(c\) deve ser um ponto crítico de\(f\). No entanto,\(c\) ser um ponto crítico não é condição suficiente\(f\) para ter uma extremidade local em\(c\). Mais adiante neste capítulo, mostraremos como determinar se uma função realmente tem um extremo local em um ponto crítico. Primeiro, no entanto, precisamos introduzir o Teorema do Valor Médio, que ajudará na análise do comportamento do gráfico de uma função.

Conceitos-chave

Uma função pode ter tanto um máximo absoluto quanto um mínimo absoluto, ter apenas um extremo absoluto ou não ter máximo absoluto ou mínimo absoluto.
Se uma função tiver uma extremidade local, o ponto em que ela ocorre deve ser um ponto crítico. No entanto, uma função não precisa ter uma extremidade local em um ponto crítico.
Uma função contínua em um intervalo fechado e limitado tem um máximo absoluto e um mínimo absoluto. Cada extremidade ocorre em um ponto crítico ou em um ponto final.

Glossário

extremo absoluto: se\(f\) tem um máximo absoluto ou mínimo absoluto em\(c\), dizemos que\(f\) tem um extremo absoluto em\(c\)

máximo absoluto: se\(f(c)≥f(x)\) para todos\(x\) no domínio de\(f\), dizemos que\(f\) tem um máximo absoluto em\(c\)

mínimo absoluto: se\(f(c)≤f(x)\) para todos\(x\) no domínio de\(f\), dizemos que\(f\) tem um mínimo absoluto em\(c\)

ponto crítico: se\(f'(c)=0\) ou\(f'(c)\) é indefinido, dizemos que c é um ponto crítico de\(f\)

teorema do valor extremo: se\(f\) é uma função contínua em um intervalo finito e fechado, então\(f\) tem um máximo absoluto e um mínimo absoluto

Teorema de Fermat: se\(f\) tem um extremo local em\(c\), então\(c\) é um ponto crítico de\(f\)

extremo local: se\(f\) tem um máximo local ou mínimo local em\(c\), dizemos que\(f\) tem um extremo local em\(c\)

máximo local: se existe um intervalo\(I\) tal que,\(f(c)≥f(x)\) para todos\(x∈I\), dizemos que\(f\) tem um máximo local em\(c\)

mínimo local: se existe um intervalo\(I\) tal que,\(f(c)≤f(x)\) para todos\(x∈I\), dizemos que\(f\) tem um mínimo local em\(c\)