4.1: Tarifas relacionadas

Last updated
Save as PDF

Page ID: 188296

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Expresse quantidades variáveis em termos de derivados.
Encontre relações entre as derivadas em um determinado problema.
Use a regra da cadeia para encontrar a taxa de variação de uma quantidade que depende da taxa de variação de outras quantidades.

Vimos que, para quantidades que estão mudando ao longo do tempo, as taxas nas quais essas quantidades mudam são dadas por derivativos. Se duas quantidades relacionadas mudarem ao longo do tempo, as taxas nas quais as quantidades mudam estão relacionadas. Por exemplo, se um balão estiver sendo preenchido com ar, tanto o raio do balão quanto o volume do balão estão aumentando. Nesta seção, consideramos vários problemas nos quais duas ou mais quantidades relacionadas estão mudando e estudamos como determinar a relação entre as taxas de variação dessas quantidades.

Configurando problemas de tarifas relacionadas

Em muitas aplicações do mundo real, as quantidades relacionadas estão mudando em relação ao tempo. Por exemplo, se considerarmos o exemplo do balão novamente, podemos dizer que a taxa de variação no volume$V$,, está relacionada à taxa de variação no raio,$r$. Nesse caso, dizemos isso$\frac{dV}{dt}$ e$\frac{dr}{dt}$ estamos relacionados às taxas porque$V$ estão relacionadas$r$ a. Aqui, estudamos vários exemplos de quantidades relacionadas que estão mudando em relação ao tempo e analisamos como calcular uma taxa de variação dada outra taxa de variação.

Exemplo$\PageIndex{1}$: Inflating a Balloon

Um balão esférico está sendo preenchido com ar na taxa constante de$2\,\text{cm}^3\text{/sec}$ (Figura$\PageIndex{1}$). Com que rapidez o raio aumenta quando o raio é$3$ cm?

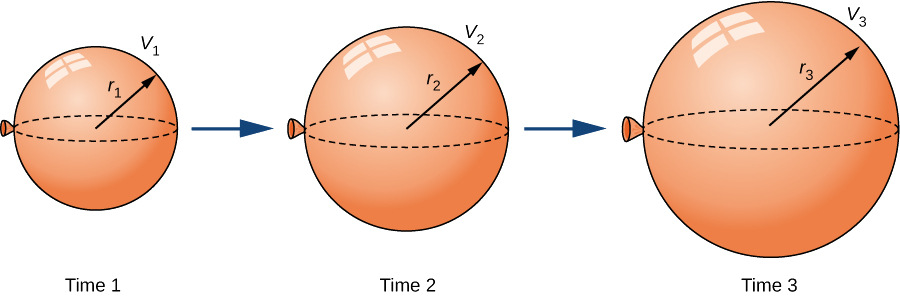
Três balões são mostrados nos tempos 1, 2 e 3. Esses balões aumentam em volume e raio à medida que o tempo aumenta. — Figura$\PageIndex{1}$: À medida que o balão está sendo preenchido com ar, tanto o raio quanto o volume estão aumentando em relação ao tempo.

Solução

O volume de uma esfera de$r$ centímetros de raio é

$V=\frac{4}{3}πr^3\,\text{cm}^3.$

Como o balão está sendo preenchido com ar, tanto o volume quanto o raio são funções do tempo. Portanto,$t$ segundos depois de começar a encher o balão com ar, o volume de ar no balão é

$V(t)=\frac{4}{3}π\big[r(t)\big]^3\text{cm}^3.$

Diferenciando os dois lados dessa equação em relação ao tempo e aplicando a regra da cadeia, vemos que a taxa de variação no volume está relacionada à taxa de mudança no raio pela equação

$V'(t)=4π\big[r(t)\big]^2r′(t).$

O balão está sendo preenchido com ar a uma taxa constante de$2 \,\text{cm}^3\text{/sec}$, então$V'(t)=2\,\text{cm}^3\text{/sec}$. Portanto,

$2\,\text{cm}^3\text{/sec}=\Big(4π\big[r(t)\big]^2\;\text{cm}^2\Big)⋅\Big(r'(t)\;\text{cm/s}\Big),$

o que implica

$r'(t)=\dfrac{1}{2π\big[r(t)\big]^2}\;\text{cm/sec}$.

Quando o raio$r=3$ cm,

$r'(t)=\dfrac{1}{18π}\;\text{cm/sec}.$

Exercício$\PageIndex{1}$

Qual é a taxa instantânea de mudança do raio quando$r=6$ cm?

Dica: $\dfrac{dr}{dt}=\dfrac{1}{2πr^2}$

Resposta: $\frac{1}{72π}$cm/seg ou aproximadamente 0,0044 cm/seg

Antes de analisar outros exemplos, vamos descrever a estratégia de solução de problemas que usaremos para resolver problemas de taxas relacionadas.

Estratégia de resolução de problemas: resolvendo um problema de taxas relacionadas

Atribua símbolos a todas as variáveis envolvidas no problema. Desenhe uma figura, se aplicável.
Indique, em termos das variáveis, as informações fornecidas e a taxa a ser determinada.
Encontre uma equação relacionando as variáveis introduzidas na etapa 1.
Usando a regra da cadeia, diferencie os dois lados da equação encontrada na etapa 3 em relação à variável independente. Essa nova equação relacionará as derivadas.
Substitua todos os valores conhecidos na equação da etapa 4 e resolva a taxa de variação desconhecida

Observe que, ao resolver um problema de taxas relacionadas, é crucial não substituir os valores conhecidos tão cedo. Por exemplo, se o valor de uma quantidade variável for substituído em uma equação antes que ambos os lados da equação sejam diferenciados, essa quantidade se comportará como uma constante e sua derivada não aparecerá na nova equação encontrada na etapa 4. Examinamos esse possível erro no exemplo a seguir.

Exemplos do processo

Vamos agora implementar a estratégia que acabamos de descrever para resolver vários problemas relacionados às taxas. O primeiro exemplo envolve um avião sobrevoando. A relação que estamos estudando é entre a velocidade do avião e a taxa na qual a distância entre o avião e uma pessoa no solo está mudando.

Exemplo$\PageIndex{2}$: An Airplane Flying at a Constant Elevation

Um avião está sobrevoando a uma elevação constante de$4000$ pés. Um homem está vendo o avião de uma posição a$3000$ pés da base de uma torre de rádio. O avião está voando horizontalmente para longe do homem. Se o avião estiver voando a uma taxa de$600$ pés/seg, em que velocidade a distância entre o homem e o avião aumenta quando o avião passa pela torre de rádio?

Solução

Etapa 1. Faça um desenho, introduzindo variáveis para representar as diferentes quantidades envolvidas.

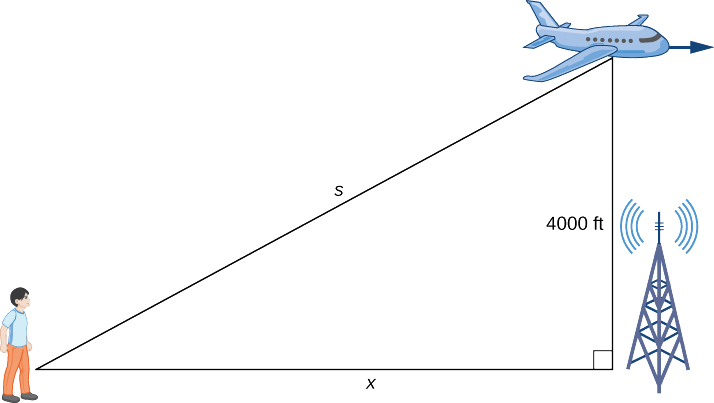
Um triângulo reto é feito com uma pessoa no chão, um avião no ar e uma torre de rádio no ângulo certo no solo. A hipotenusa é s, a distância no solo entre a pessoa e a torre de rádio é x e o lado oposto à pessoa (ou seja, a altura do solo até o avião) é de 4000 pés. — Figura$\PageIndex{2}$: Um avião está voando a uma altura constante de$4000$ pés. A distância entre a pessoa e o avião e a pessoa e o lugar no solo diretamente abaixo do avião estão mudando. Nós denotamos essas quantidades com as variáveis$s$ e$x$, respectivamente.

Conforme mostrado,$x$ indica a distância entre o homem e a posição no solo diretamente abaixo do avião. A variável$s$ indica a distância entre o homem e o avião. Note que ambos$x$ e$s$ são funções do tempo. Não introduzimos uma variável para a altura do avião porque ele permanece em uma elevação constante de$4000$ pés. Como a altura de um objeto acima do solo é medida como a menor distância entre o objeto e o solo, o segmento de linha de comprimento de 4000 pés é perpendicular ao segmento de linha de$x$ pés de comprimento, criando um triângulo reto.

Etapa 2. Uma vez que$x$ denota a distância horizontal entre o homem e o ponto no solo abaixo do plano,$dx/dt$ representa a velocidade do avião. Somos informados de que a velocidade do avião é$600$ pés/seg. Portanto,$\frac{dx}{dt}=600$ pés/seg. Como somos solicitados a encontrar a taxa de variação na distância entre o homem e o avião quando o avião está diretamente acima da torre de rádio, precisamos descobrir$ds/dt$ quando$x=3000$ pés.

Etapa 3. A partir da figura, podemos usar o teorema de Pitágoras para escrever uma equação relacionando$x$ e$s$:

$[x(t)]^2+4000^2=[s(t)]^2.$

Etapa 4. Diferenciando essa equação em relação ao tempo e usando o fato de que a derivada de uma constante é zero, chegamos à equação

\[x\frac{dx}{dt}=s\frac{ds}{dt}.\nonumber \]

Etapa 5. Encontre a taxa na qual a distância entre o homem e o avião está aumentando quando o avião está diretamente sobre a torre de rádio. Isso é, encontre$\frac{ds}{dt}$ quando$x=3000$ ft. Como a velocidade do avião é$600$ pés/seg, sabemos que$\frac{dx}{dt}=600$ pés/seg. Não recebemos um valor explícito para$s$; no entanto, como estamos tentando descobrir$\frac{ds}{dt}$ quando$x=3000$ pés, podemos usar o teorema de Pitágoras para determinar a distância$s$ quando$x=3000$ pés e a altura são$4000$ pés. Resolvendo a equação

$3000^2+4000^2=s^2$

pois$s$, temos$s=5000$ pés no momento do interesse. Usando esses valores, concluímos que$ds/dt$

é uma solução da equação

$(3000)(600)=(5000)⋅\dfrac{ds}{dt}$.

Portanto,

$\dfrac{ds}{dt}=\dfrac{3000⋅600}{5000}=360\,\text{ft/sec}.$

Nota: Ao resolver problemas de taxas relacionadas, é importante não substituir os valores pelas variáveis muito cedo. Por exemplo, na etapa 3, relacionamos as quantidades variáveis$x(t)$ e$s(t)$ pela equação

$[x(t)]^2+4000^2=[s(t)]^2.$

Como o avião permanece em uma altura constante, não é necessário introduzir uma variável para a altura, e podemos usar a constante 4000 para denotar essa quantidade. No entanto, as outras duas quantidades estão mudando. Se substituíssemos erroneamente$x(t)=3000$ a equação antes de diferenciar, nossa equação teria sido

$3000^2+4000^2=[s(t)]^2.$

Depois de diferenciar, nossa equação se tornaria

$0=s(t)\dfrac{ds}{dt}.$

Como resultado, concluiríamos incorretamente que$\frac{ds}{dt}=0.$

Exercício$\PageIndex{2}$

Qual é a velocidade do avião se a distância entre a pessoa e o avião estiver aumentando na taxa de$300$ pés/seg?

Dica: $\dfrac{ds}{dt}=300$pés/seg

Responda: $500$pés/seg

Agora voltamos ao problema envolvendo o lançamento do foguete desde o início do capítulo.

Exemplo$\PageIndex{3}$: Chapter Opener - A Rocket Launch

Um foguete é lançado para que ele suba verticalmente. A câmera está posicionada a$5000$ pés da plataforma de lançamento. Quando o foguete está$1000$ pés acima da plataforma de lançamento, sua velocidade é$600$ pés/seg.

Uma foto de um foguete decolando. — Figura$\PageIndex{3}$: (crédito: modificação do trabalho de Steve Jurvetson, Wikimedia Commons)

Encontre a taxa de mudança necessária do ângulo da câmera em função do tempo para que ela permaneça focada no foguete.

Solução

Etapa 1. Faça um desenho apresentando as variáveis.

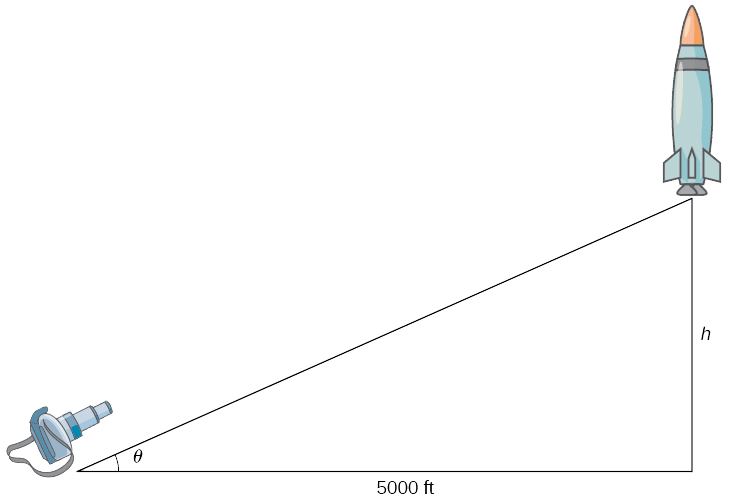
Um triângulo reto é formado com uma câmera em um dos ângulos não retos e um foguete no outro ângulo não reto. O ângulo com a câmera tem medida θ. A distância do foguete ao solo é h; observe que este é o lado oposto ao ângulo com a medida θ. O lado adjacente ao ângulo com a medida θ é de 5000 pés. — Figura$\PageIndex{4}$: A câmera está posicionada a$5000$ pés da plataforma de lançamento do foguete. A altura do foguete e o ângulo da câmera estão mudando em relação ao tempo. Nós denotamos essas quantidades com as variáveis$h$ e$θ$, respectivamente.

Vamos$h$ indicar a altura do foguete acima da plataforma de lançamento e$θ$ ser o ângulo entre a lente da câmera e o solo.

Etapa 2. Estamos tentando encontrar a taxa de mudança no ângulo da câmera em relação ao tempo em que o foguete está a 1000 pés do chão. Isso é, precisamos descobrir$\frac{dθ}{dt}$ quando$h=1000$ ft. Nesse momento, sabemos que a velocidade do foguete é$\frac{dh}{dt}=600$ pés/seg.

Etapa 3. Agora precisamos encontrar uma equação relacionando as duas quantidades que estão mudando em relação ao tempo:$h$$θ$ e. Como podemos criar essa equação? Usando o fato de termos desenhado um triângulo reto, é natural pensar em funções trigonométricas. Lembre-se de que$\tan θ$ é a razão entre o comprimento do lado oposto do triângulo e o comprimento do lado adjacente. Assim, temos

$\tan θ=\dfrac{h}{5000}$.

Isso nos dá a equação

$h=5000\tan θ.$

Etapa 4. Diferenciando essa equação em relação ao tempo$t$, obtemos

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}$.

Etapa 5. Queremos descobrir$\frac{dθ}{dt}$ quando$h=1000$ pés. No momento, sabemos que$\frac{dh}{dt}=600$ pés/seg. Precisamos determinar$\sec^2θ$. Lembre-se de que$\sec θ$ é a proporção entre o comprimento da hipotenusa e o comprimento do lado adjacente. Sabemos que o comprimento do lado adjacente é de$5000$ pés. Para determinar o comprimento da hipotenusa, usamos o teorema de Pitágoras, onde o comprimento de uma perna é$5000$ pés, o comprimento da outra perna é$h=1000$ pés e o comprimento da hipotenusa é$c$ pés, conforme mostrado na figura a seguir.

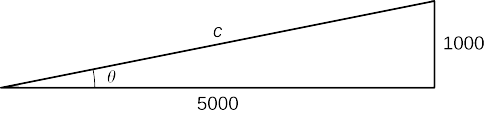
$Um triângulo reto tem um ângulo com medida θ. A hipotenusa é c, o comprimento do lado oposto ao ângulo com medida θ é 1000 e o lado adjacente ao ângulo com medida θ é 5000.$

Nós vemos isso

$1000^2+5000^2=c^2$

e concluímos que a hipotenusa é

$c=1000\sqrt{26}\,\text{ft}.$

Portanto, quando$h=1000,$ temos

$\sec^2θ=\left(\dfrac{1000\sqrt{26}}{5000}\right)^2=\dfrac{26}{25}.$

Lembre-se da etapa 4 que a equação relacionada$\frac{dθ}{dt}$ aos nossos valores conhecidos é

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}.$

Quando$h=1000$ pés, sabemos que$\frac{dh}{dt}=600$ pés/seg$\sec^2θ=\frac{26}{25}$ e. Substituindo esses valores na equação anterior, chegamos à equação

$600=5000\left(\frac{26}{25}\right)\dfrac{dθ}{dt}$.

Portanto,$\dfrac{dθ}{dt}=\dfrac{3}{26}$ rad/sec.

Exercício$\PageIndex{3}$

Que taxa de mudança é necessária para o ângulo de elevação da câmera se a câmera for colocada no solo a uma distância de$4000$ pés da plataforma de lançamento e a velocidade do foguete for$500$ pés/seg quando o foguete estiver a$2000$ pés do solo?

Dica: Descubra$\frac{dθ}{dt}$ quando$h=2000$ ft. Naquela época,$\frac{dh}{dt}=500$ pés/seg.

Responda: $\frac{1}{10}$rad/seg

No próximo exemplo, consideramos a drenagem da água de um funil em forma de cone. Comparamos a taxa na qual o nível de água no cone está diminuindo com a taxa na qual o volume de água está diminuindo.

Exemplo$\PageIndex{4}$: Water Draining from a Funnel

A água está drenando do fundo de um funil em forma de cone na proporção de$0.03\,\text{ft}^3\text{/sec}$. A altura do funil é$2$ pés e o raio na parte superior do funil é$1$ ft. Em que taxa a altura da água no funil muda quando a altura da água é de$\frac{1}{2}$ pés?

Solução

Etapa 1: Desenhe uma imagem introduzindo as variáveis.

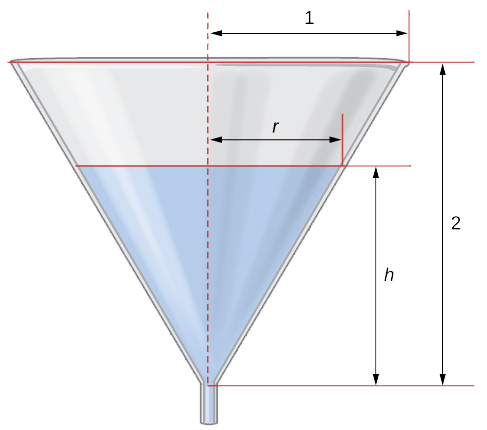
Um funil é mostrado com altura 2 e raio 1 na parte superior. O funil tem água até a altura h, ponto em que o raio é r. — Figura$\PageIndex{5}$: A água está drenando de um funil de altura$2$ ft e raio$1$ ft. A altura da água e o raio da água estão mudando com o tempo. Denotamos essas quantidades com as variáveis$h$ e$r$, respectivamente.

Deixe$h$ indicar a altura da água no funil, r denotar o raio da água em sua superfície e$V$ indicar o volume da água.

Etapa 2: Precisamos determinar$\frac{dh}{dt}$ quando$h=\frac{1}{2}$ pés. Sabemos que$\frac{dV}{dt}=−0.03$ pés/seg.

Etapa 3: O volume de água no cone é

$V=\frac{1}{3}πr^2h.$

A partir da figura, vemos que temos triângulos semelhantes. Portanto, a proporção dos lados nos dois triângulos é a mesma. Portanto,$\frac{r}{h}=\frac{1}{2}$ ou$r=\frac{h}{2}.$ usando esse fato, a equação do volume pode ser simplificada para

$V=\frac{1}{3}π\left(\frac{h}{2}\right)^2h=\frac{π}{12}h^3$.

Etapa 4: Aplicando a regra da cadeia ao diferenciar os dois lados dessa equação em relação ao tempo$t$, obtemos

\[\frac{dV}{dt}=\frac{π}{4}h^2\frac{dh}{dt}.\nonumber \]

Etapa 5: Queremos descobrir$\frac{dh}{dt}$ quando$h=\frac{1}{2}$ pés. Como a água está saindo na proporção de$0.03\,\text{ft}^3\text{/sec}$, nós sabemos disso$\frac{dV}{dt}=−0.03\,\text{ft}^3\text{/sec}$. Portanto,

\[−0.03=\frac{π}{4}\left(\frac{1}{2}\right)^2\dfrac{dh}{dt},\nonumber \]

o que implica

\[−0.03=\frac{π}{16}\dfrac{dh}{dt}.\nonumber \]

Daqui resulta que

\[\dfrac{dh}{dt}=−\frac{0.48}{π}=−0.153\,\text{ft/sec}.\nonumber \]

Exercício$\PageIndex{4}$

Em que taxa a altura da água muda quando a altura da água é de$\frac{1}{4}$ pés?

Dica: Precisamos descobrir$\frac{dh}{dt}$ quando$h=\frac{1}{4}.$

Responda: $−0.61$pés/seg

Conceitos-chave

Para resolver um problema de tarifas relacionado, primeiro desenhe uma imagem que ilustre a relação entre as duas ou mais quantidades relacionadas que estão mudando em relação ao tempo.
Em termos de quantidades, indique as informações fornecidas e a taxa a ser encontrada.
Encontre uma equação relacionando as quantidades.
Use a diferenciação, aplicando a regra da cadeia conforme necessário, para encontrar uma equação que relacione as taxas.
Certifique-se de não substituir uma quantidade variável por uma das variáveis até encontrar uma equação relacionada às taxas.

Glossário

tarifas relacionadas: são taxas de variação associadas a duas ou mais quantidades relacionadas que estão mudando ao longo do tempo

Exemplo\(\PageIndex{1}\): Inflating a Balloon

Exercício\(\PageIndex{1}\)

Estratégia de resolução de problemas: resolvendo um problema de taxas relacionadas

Exemplo\(\PageIndex{2}\): An Airplane Flying at a Constant Elevation

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\): Chapter Opener - A Rocket Launch

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\): Water Draining from a Funnel

Exercício\(\PageIndex{4}\)