4.1E: Exercícios para a Seção 4.1

Last updated
Save as PDF

Page ID: 188309

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 3, encontre as quantidades para a equação dada.

1) Encontre$\frac{dy}{dt}$ em$x=1$ e$y=x^2+3$ se$\frac{dx}{dt}=4.$

Resposta: $\dfrac{dy}{dt} = 8$

2) Encontre$\frac{dx}{dt}$ em$x=−2$ e$y=2x^2+1$ se$\frac{dy}{dt}=−1.$

3) Encontre$\frac{dz}{dt}$ em$(x,y)=(1,3)$$\frac{dx}{dt}=4$ e$z^2=x^2+y^2$ se$\frac{dy}{dt}=3$ e.

Resposta: $\dfrac{dz}{dt} = \frac{13}{\sqrt{10}}$

Nos exercícios 4 a 15, esboce a situação, se necessário, e use as taxas relacionadas para resolver as quantidades.

4) [T] Se dois resistores elétricos estiverem conectados em paralelo, a resistência total (medida em ohms, indicada pela letra maiúscula grega ômega$Ω$) é dada pela equação$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}.$ If$R_1$ está aumentando a uma taxa de$0.5Ω/\text{min}$ e$R_2$ diminui a uma taxa de$1.1Ω/\text{min}$, em que taxa a resistência total muda quando$R_1=20Ω$ e$R_2=50Ω/\text{min}$?

5) Uma escada$10$ de 5 pés está encostada em uma parede. Se a parte superior da escada deslizar pela parede a uma taxa de$2$ pés/seg, com que rapidez a parte inferior se move ao longo do solo quando a parte inferior da escada está a$5$ pés da parede?

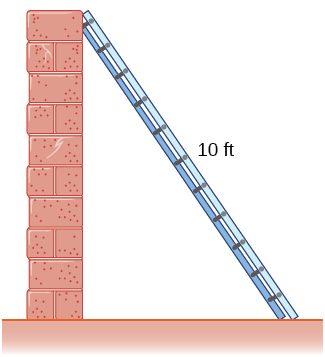
$Um triângulo reto é formado por uma escada encostada em uma parede de tijolos. A escada forma a hipotenusa e tem 10 pés de comprimento.$

Resposta: $2\sqrt{3}$pés/seg

6) Uma escada$25$ de 3 pés está encostada em uma parede. Se empurrarmos a escada em direção à parede a uma taxa de$1$ pés/seg, e a parte inferior da escada estiver inicialmente a$20$ pés de distância da parede, com que rapidez a escada sobe na parede$5$ segundos depois de começarmos a empurrar?

7) Dois aviões estão voando no ar na mesma altura: o avião A está voando para o leste a$250$ mi/h e o avião B está voando para o norte a$300$ mi/h. Se ambos estiverem indo para o mesmo aeroporto, localizado a$30$ milhas a leste do avião A e$40$ milhas ao norte do avião B, em que taxa é o a distância entre os aviões está mudando?

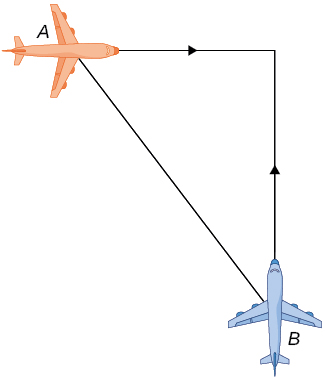
$Um triângulo reto é formado por dois aviões A e B se movendo perpendicularmente um ao outro. A hipotenusa é a distância entre os planos A e B. Os outros lados são extensões do caminho de cada plano até que eles se encontrem.$

Resposta: A distância está diminuindo em$390$ mi/h.

8) Você e um amigo estão indo de bicicleta até um restaurante que você acha que é o leste; seu amigo acha que o restaurante fica ao norte. Vocês dois partem do mesmo ponto, com você andando a$16$ mph leste e seu amigo andando$12$ mph para o norte. Depois de viajar$4$ mi, em que ritmo a distância entre vocês está mudando?

9) Dois ônibus estão dirigindo por rodovias paralelas que estão a$5$ quilômetros de distância, um indo para o leste e o outro para o oeste. Supondo que cada ônibus dirija uma$55$ mph constante, encontre a taxa na qual a distância entre os ônibus muda quando eles estão a$13$ quilômetros de distância (enquanto o corvo voa), indo um em direção ao outro.

Resposta: A distância entre eles diminui a uma taxa de$\frac{1320}{13}≈101.5$ mph.

10) Uma pessoa de$6$$10$ -ft de altura se afasta de um poste de luz a uma taxa constante de$3$ pés/seg. Qual é a taxa em que a ponta da sombra se afasta do poste quando a pessoa está a$10$ pés de distância do poste?

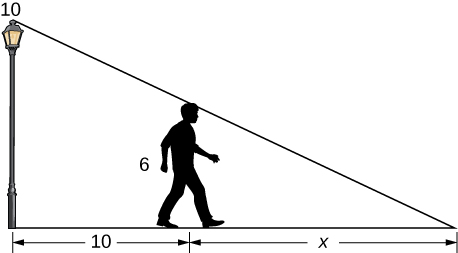
$É mostrado um poste de luz com 10 pés de altura. À sua direita, há uma pessoa com 6 pés de altura. Há uma linha do topo do poste que toca a parte superior da cabeça da pessoa e depois continua até o chão. O comprimento do final desta linha até onde o poste toca o solo é 10 + x. A distância do poste até a pessoa no chão é 10 e a distância da pessoa até o final da linha é x.$

11) Usando o problema anterior, qual é a taxa na qual a ponta da sombra se afasta da pessoa quando a pessoa está a$10$ pés do poste?

Resposta: $\frac{9}{2}$pés/seg

12) Uma pessoa$5$ de um metro de altura caminha em direção a uma parede a uma taxa de$2$ pés/seg. Um holofote está localizado no chão, a poucos$40$ metros da parede. Com que rapidez a altura da sombra da pessoa na parede muda quando a pessoa está a$10$ pés da parede?

13) Usando o problema anterior, qual é a taxa na qual a sombra muda quando a pessoa está a$10$ pés da parede, se a pessoa está se afastando da parede a uma taxa de$2$ pés/seg?

Resposta: Ela cresce a uma taxa$\frac{4}{9}$ ft/seg

14) Um helicóptero partindo do solo está subindo diretamente no ar a uma taxa de$25$ pés/seg. Você está correndo no chão começando diretamente embaixo do helicóptero a uma taxa de$10$ pés/seg. Encontre a taxa de variação da distância entre o helicóptero e você após um$5$ segundo.

15) Usando o problema anterior, supondo que o helicóptero esteja subindo novamente a uma taxa de$25$ pés/seg e você esteja correndo no solo começando diretamente embaixo do helicóptero a uma taxa de$10$ pés/seg, qual é a taxa na qual a distância entre você e o helicóptero está mudando quando o helicóptero está mudando quando o helicóptero subiu para uma altura de$60$ pés no ar, assumindo que, inicialmente, estava$30$ pés acima de você?

Resposta: A distância está aumentando em$\frac{135\sqrt{26}}{26}$ pés/seg

Nos exercícios 16 a 24, desenhe e rotule diagramas para ajudar a resolver os problemas relacionados às taxas.

16) O lado de um cubo aumenta a uma taxa de$\frac{1}{2}$ m/seg. Encontre a taxa na qual o volume do cubo aumenta quando o lado do cubo é$4$ m.

17) O volume de um cubo diminui a uma taxa de$10 \text{ m}^3$ /seg. Encontre a taxa na qual o lado do cubo muda quando o lado do cubo é$2$ m.

Resposta: $−\frac{5}{6}$m/seg

18) O raio de um círculo aumenta a uma taxa de$2$ m/seg. Encontre a taxa na qual a área do círculo aumenta quando o raio é$5$ m.

19) O raio de uma esfera diminui a uma taxa de$3$ m/seg. Encontre a taxa na qual a área da superfície diminui quando o raio é$10$ m.

Resposta: $240π \,\text{m}^2\text{/sec}$

20) O raio de uma esfera aumenta a uma taxa de$1$ m/seg. Encontre a taxa na qual o volume aumenta quando o raio é$20$ m.

21) O raio de uma esfera está aumentando a uma taxa de$9$ cm/seg. Encontre o raio da esfera quando o volume e o raio da esfera estão aumentando na mesma taxa numérica.

Resposta: $\frac{1}{2\sqrt{π}}$cm

22) A base de um triângulo está encolhendo a uma taxa de$1$ cm/min e a altura do triângulo está aumentando a uma taxa de$5$ cm/min. Encontre a taxa na qual a área do triângulo muda quando a altura é$22$ cm e a base é$10$ cm.

23) Um triângulo tem dois lados constantes de comprimento$3$ pés e$5$ pés. O ângulo entre esses dois lados está aumentando a uma taxa de$0.1$ rad/seg. Encontre a taxa na qual a área do triângulo está mudando quando o ângulo entre os dois lados é$π/6.$

Resposta: A área está aumentando em um ritmo$\frac{3\sqrt{3}}{8}\,\text{ft}^2\text{/sec}$.

24) Um triângulo tem uma altura que está aumentando a uma taxa de$2$ cm/seg e sua área está aumentando a uma taxa de$4 \,\text{cm}^2\text{/sec}$. Encontre a taxa na qual a base do triângulo está mudando quando a altura do triângulo é$4$ cm e a área é$20 \,\text{cm}^2$.

Nos exercícios 25 a 27, considere um cone direito invertido que esteja vazando água. (Invertido significa que a ponta do cone está voltada para baixo, como um funil.) As dimensões do tanque cônico são uma altura de 16 pés e um raio de 5 pés.

25) Com que rapidez a profundidade da água muda quando a água tem$10$ pés de altura se o cone vazar água a uma taxa de$10 \,\text{ft}^3\text{/min}$?

Resposta: A profundidade da água diminui em$\frac{128}{125π}$ pés/min.

26) Encontre a taxa na qual a área da superfície da água muda quando a água está com$10$ pés de altura se o cone vazar água a uma taxa de$10 \,\text{ft}^3\text{/min}$.

27) Se o nível da água estiver diminuindo a uma taxa de$3$ pol/min quando a profundidade da água estiver em$8$ pés, determine a taxa na qual a água está vazando do cone.

Resposta: O volume está diminuindo a uma taxa de$\frac{25π}{16}\,\text{ft}^3\text{/min}$.

28) Um cilindro vertical está vazando água a uma taxa de$1 \,\text{ft}^3\text{/sec}$. Se o cilindro tiver uma altura de$10$ pés e um raio de$1$ pés, em que taxa a altura da água muda quando a altura é$6$ pés?

29) Um cilindro está vazando água, mas você não consegue determinar em que velocidade. O cilindro tem uma altura de$2$ m e um raio de$2$ m. Encontre a taxa na qual a água está vazando para fora do cilindro se a taxa na qual a altura está diminuindo for$10$ cm/min quando a altura for$1$ m.

Resposta: A água sai rapidamente$\frac{2π}{5}\,\text{m}^3\text{/min}$.

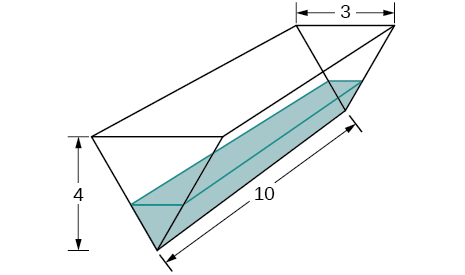
30) Uma calha tem extremidades em forma de triângulos isósceles, com largura$3$ m e altura$4$ m, e a calha tem$10$ m de comprimento. A água está sendo bombeada para a calha a uma taxa de$5\,\text{m}^3\text{/min}$. Em que velocidade a altura da água muda quando a água tem$1$ m de profundidade?

$Uma calha é mostrada com extremidades em forma de triângulos isósceles. Esses triângulos têm largura 3 e altura 4. A calha é composta por retângulos de comprimento 10. Há um pouco de água na calha.$

31) Um tanque tem a forma de uma pirâmide quadrada invertida, com base de$4$ m por$4$ m e altura de$12$ m (veja a figura a seguir). Com que rapidez a altura aumenta quando a água tem$2$ m de profundidade se a água estiver sendo bombeada a uma taxa de$\frac{2}{3} \text{ m}^3$ /seg?

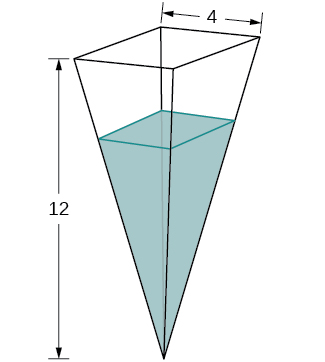
$Uma pirâmide quadrada invertida é mostrada com lados quadrados de comprimento 4 e altura 12. Há uma quantidade não especificada de água dentro da forma.$

Resposta: $\frac{3}{2}$m/seg

Para os exercícios 32 a 34, considere uma piscina em forma de metade inferior de uma esfera, que está sendo preenchida a uma taxa de$25 \,\text{ft}^3$ /min. O raio da piscina é de$10$ pés.

32) Encontre a taxa na qual a profundidade da água está mudando quando a água tem uma profundidade de$5$ pés.

33) Encontre a taxa na qual a profundidade da água está mudando quando a água tem uma profundidade de$1$ pés.

Resposta: $\frac{25}{19π}$pés/min

34) Se a altura estiver aumentando a uma taxa de$1$ pol/seg quando a profundidade da água for de$2$ pés, encontre a taxa na qual a água está sendo bombeada.

35) O cascalho está sendo descarregado de um caminhão e cai em uma pilha em forma de cone a uma taxa de$10 \,\text{ft}^3/\text{min}$. O raio da base do cone é três vezes a altura do cone. Encontre a taxa na qual a altura do cascalho muda quando a pilha tem uma altura de$5$ pés.

Resposta: $\frac{2}{45π}$pés/min

36) Usando uma configuração semelhante ao problema anterior, encontre a taxa na qual o cascalho está sendo descarregado se a pilha tiver$5$ pés de altura e a altura estiver aumentando a uma taxa de$4$ pol/min.

Nos exercícios 37 a 41, desenhe as situações e resolva os problemas relacionados à taxa.

37) Você está parado no chão e está vendo um pássaro voar horizontalmente a uma taxa de$10$ m/seg. O pássaro está localizado$40$ m acima da sua cabeça. Com que rapidez o ângulo de elevação muda quando a distância horizontal entre você e o pássaro é$9$ m?

Resposta: O ângulo diminui em$\frac{400}{1681}$ rad/seg.

38) Você fica a$40$ pés de um foguete de garrafa no chão e observa como ele decola verticalmente no ar a uma taxa de$20$ pés/seg. Encontre a taxa na qual o ângulo de elevação muda quando o foguete está a$30$ pés no ar.

39) Um farol,$L$, fica em uma ilha a$4$ milhas de distância do ponto mais próximo$P$,, na praia (veja a imagem a seguir). Se a luz do farol girar no sentido horário a uma taxa constante de$10$ rotações/min, com que rapidez o feixe de luz se move pela praia a$2$ quilômetros de distância do ponto mais próximo da praia?

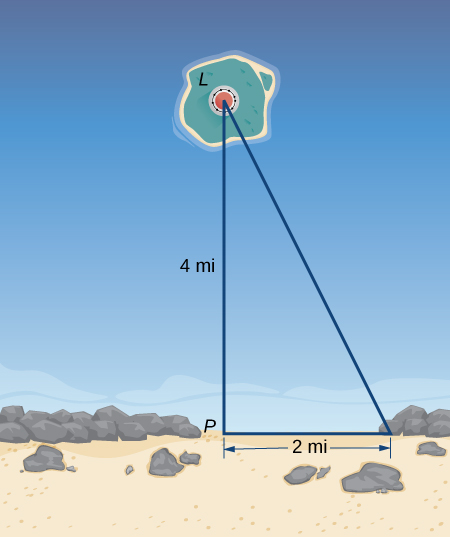
$Um triângulo reto é formado por um farol L, um ponto P na costa que é perpendicular à linha do farol até a costa e um ponto 2 milhas à direita do ponto P. A distância de P a L é de 4 milhas.$

Resposta: $100π$mínimo/min

40) Usando a mesma configuração do problema anterior, determine a que velocidade o feixe de luz se move pela praia a$1$ quilômetros de distância do ponto mais próximo da praia.

41) Você está caminhando até um ponto de ônibus na esquina em ângulo reto. Você se move para o norte a uma taxa de$2$ m/seg e está$20$ m ao sul da interseção. O ônibus viaja para o oeste a uma taxa de$10$ m/seg de distância do cruzamento - você perdeu o ônibus! Qual é a taxa na qual o ângulo entre você e o ônibus muda quando você está$20$ m ao sul do cruzamento e o ônibus está$10$ m a oeste do cruzamento?

Resposta: O ângulo está mudando a uma taxa de$\frac{11}{25}$ rad/seg.

Nos exercícios 42 a 45, consulte a figura do diamante de beisebol, que tem lados de 90 pés.

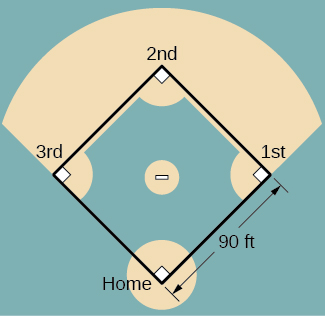
$Um campo de beisebol é mostrado, com as bases rotuladas Home, 1st, 2nd e 3rd formando um quadrado com comprimentos laterais de 90 pés.$

42) [T] Um batedor acerta uma bola em direção à terceira base a$75$ pés/seg e corre em direção à primeira base a uma taxa de$24$ pés/seg. Em que velocidade a distância entre a bola e o batedor muda quando o$2$ segundo passa?

43) [T] Um batedor acerta uma bola em direção à segunda base a$80$ pés/seg e corre em direção à primeira base a uma taxa de$30$ pés/seg. Em que velocidade a distância entre a bola e o batedor muda quando o corredor percorre um terço da distância até a primeira base? (Dica: lembre-se da lei dos cossenos.)

Resposta: A distância está aumentando a uma taxa de$62.50$ pés/seg.

44) [T] Um batedor bate na bola e corre em direção à primeira base a uma velocidade de$22$ pés/seg. Em que velocidade a distância entre o corredor e a segunda base muda quando o corredor corre por$30$ pés?

45) [T] Os corredores começam na primeira e na segunda base. Quando a bola de beisebol é atingida, o corredor na primeira base corre a uma velocidade de$18$ pés/seg em direção à segunda base e o corredor na segunda base corre a uma velocidade de$20$ pés/seg em direção à terceira base. A que velocidade a distância entre os corredores muda 1 segundo após a bola ser atingida?

Resposta: A distância está diminuindo a uma taxa de$11.99$ pés/seg.