4.2: Aproximações lineares e diferenciais
- Page ID
- 188297
- Descreva a aproximação linear de uma função em um ponto.
- Escreva a linearização de uma determinada função.
- Desenhe um gráfico que ilustre o uso de diferenciais para aproximar a mudança em uma quantidade.
- Calcule o erro relativo e o erro percentual usando uma aproximação diferencial.
Acabamos de ver como os derivados nos permitem comparar quantidades relacionadas que estão mudando com o tempo. Nesta seção, examinamos outra aplicação de derivadas: a capacidade de aproximar funções localmente por funções lineares. As funções lineares são as funções mais fáceis de trabalhar, portanto, elas fornecem uma ferramenta útil para aproximar os valores das funções. Além disso, as ideias apresentadas nesta seção são generalizadas posteriormente no texto, quando estudamos como aproximar funções por polinômios de maior grau. Introdução às séries de potências e funções.
Aproximação linear de uma função em um ponto
Considere uma função\(f\) que seja diferenciável em um ponto\(x=a\). Lembre-se de que a reta tangente ao gráfico de\(f\) at\(a\) é dada pela equação
\[y=f(a)+f'(a)(x−a). \nonumber \]
Por exemplo, considere a função\(f(x)=\frac{1}{x}\) at\(a=2\). Uma vez que\(f\) é diferenciável em\(x=2\) e\(f'(x)=−\frac{1}{x^2}\), vemos isso\(f'(2)=−\frac{1}{4}\). Portanto, a reta tangente ao gráfico de\(f\) at\(a=2\) é dada pela equação
\[y=\frac{1}{2}−\frac{1}{4}(x−2). \nonumber \]
A figura\(\PageIndex{1a}\) mostra um gráfico de\(f(x)=\frac{1}{x}\) junto com a reta tangente a\(f\) at\(x=2\). Observe que para\(x\) near\(2\), o gráfico da reta tangente está próximo ao gráfico de\(f\). Como resultado, podemos usar a equação da reta tangente\(f(x)\) para\(x\) aproximar\(2\). Por exemplo\(x=2.1\), se o\(y\) valor do ponto correspondente na linha tangente for
\[y=\frac{1}{2}−\frac{1}{4}(2.1−2)=0.475. \nonumber \]
O valor real de\(f(2.1)\) é dado por
\[f(2.1)=\frac{1}{2.1}≈0.47619. \nonumber \]
Portanto, a reta tangente nos dá uma aproximação bastante boa de\(f(2.1)\) (Figura\(\PageIndex{1b}\)). No entanto, observe que para valores\(x\) distantes\(2\), a equação da reta tangente não nos dá uma boa aproximação. Por exemplo\(x=10\), se o\(y\) valor -do ponto correspondente na linha tangente for
\[y=\frac{1}{2}−\frac{1}{4}(10−2)=\frac{1}{2}−2=−1.5, \nonumber \]
enquanto que o valor da função at\(x=10\) é\(f(10)=0.1.\)
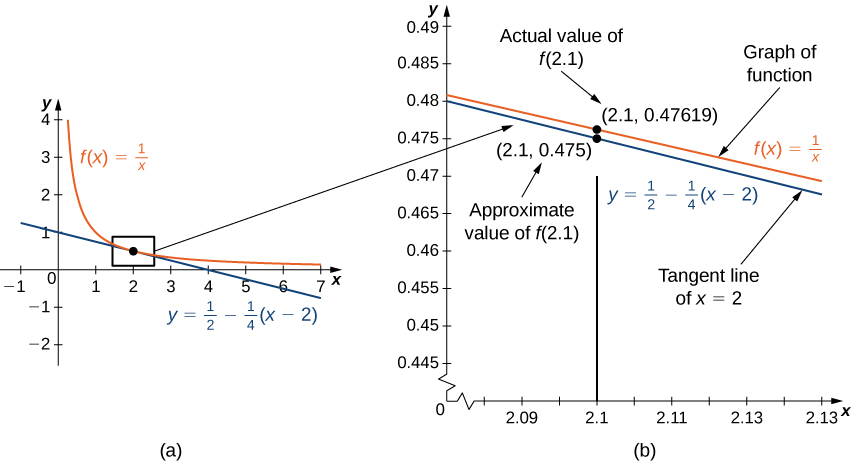
Em geral, para uma função diferenciável\(f\), a equação da reta tangente a\(f\) at\(x=a\) pode ser usada\(f(x)\) para aproximar a\(x\) proximidade\(a\). Portanto, podemos escrever
\(f(x)≈f(a)+f'(a)(x−a)\)por\(x\) perto\(a\).
Chamamos a função linear
\[L(x)=f(a)+f'(a)(x−a) \label{linearapprox} \]
a aproximação linear, ou aproximação de reta tangente, de\(f\) at\(x=a\). Essa função também\(L\) é conhecida como linearização de\(f\) em\(x=a.\)
Para mostrar o quão útil a aproximação linear pode ser, veremos como encontrar a aproximação linear para\(f(x)=\sqrt{x}\) em\(x=9.\)
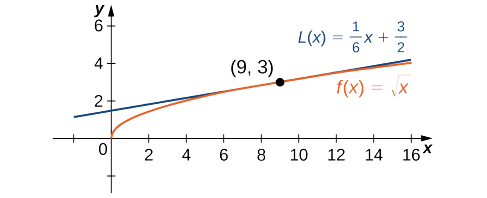
Encontre a aproximação linear de\(f(x)=\sqrt{x}\) at\(x=9\) e use a aproximação para estimar\(\sqrt{9.1}\).
Solução
Como estamos procurando a aproximação linear\(x=9,\) usando a Equação\ ref {linearapprox}, sabemos que a aproximação linear é dada por
\[L(x)=f(9)+f'(9)(x−9). \nonumber \]
Precisamos encontrar\(f(9)\) e\(f'(9).\)
\(f(x)=\sqrt{x}⇒f(9)=\sqrt{9}=3\)
\(f'(x)=\frac{1}{2\sqrt{x}}⇒f'(9)=\frac{1}{2\sqrt{9}}=\frac{1}{6}\)
Portanto, a aproximação linear é dada pela Figura\(\PageIndex{2}\).
\[L(x)=3+\frac{1}{6}(x−9) \nonumber \]
Usando a aproximação linear, podemos estimar\(\sqrt{9.1}\) escrevendo
\[\sqrt{9.1}=f(9.1)≈L(9.1)=3+\frac{1}{6}(9.1−9)≈3.0167. \nonumber \]
Análise
Usando uma calculadora, o valor de\(\sqrt{9.1}\) até quatro casas decimais é\(3.0166\). O valor dado pela aproximação linear,\(3.0167\), é muito próximo ao valor obtido com uma calculadora, então parece que usar essa aproximação linear é uma boa maneira de estimar\(\sqrt{x}\), pelo menos para x near\(9\). Ao mesmo tempo, pode parecer estranho usar uma aproximação linear quando podemos simplesmente apertar alguns botões em uma calculadora para avaliar\(\sqrt{9.1}\). No entanto, como a calculadora avalia\(\sqrt{9.1}\)? A calculadora usa uma aproximação! Na verdade, calculadoras e computadores usam aproximações o tempo todo para avaliar expressões matemáticas; eles usam apenas aproximações de maior grau.
Encontre a aproximação linear local para\(f(x)=\sqrt[3]{x}\) at\(x=8\). Use-o para\(\sqrt[3]{8.1}\) aproximar cinco casas decimais.
- Dica
-
\(L(x)=f(a)+f'(a)(x−a)\)
- Resposta
-
\(L(x)=2+\frac{1}{12}(x−8);\)\(2.00833\)
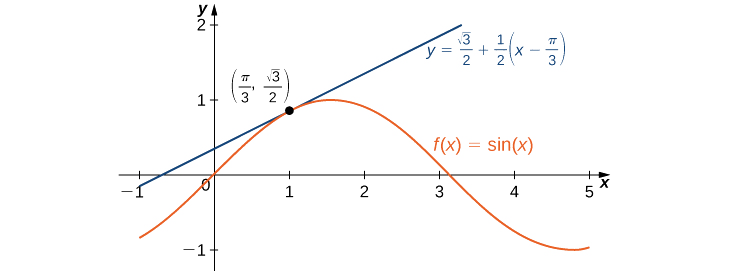
Encontre a aproximação linear de\(f(x)=\sin x \) at\(x=\frac{π}{3}\) e use-a para aproximar\(\sin(62°).\)
Solução
Primeiro, notamos que, como\(\frac{π}{3}\) rad é equivalente a\(60°\), usar a aproximação linear em\(x=π/3\) parece razoável. A aproximação linear é dada por
\(L(x)=f(\frac{π}{3})+f'(\frac{π}{3})(x−\frac{π}{3}).\)
Nós vemos isso
\(f(x)=\sin x ⇒f(\frac{π}{3})=\sin(\frac{π}{3})=\frac{\sqrt{3}}{2}\)
\(f'(x)=\cos x ⇒f'(\frac{π}{3})=\cos(\frac{π}{3})=\frac{1}{2}\)
Portanto, a aproximação linear de\(f\) at\(x=π/3\) é dada pela Figura\(\PageIndex{3}\).
\(L(x)=\frac{\sqrt{3}}{2}+\frac{1}{2}(x−\frac{π}{3})\)
Para estimar\(\sin(62°)\) o uso\(L\), precisamos primeiro\(62°\) converter em radianos. Temos\(62°=\frac{62π}{180}\) radianos, então a estimativa para\(\sin(62°)\) é dada por
\(\sin(62°)=f(\frac{62π}{180})≈L(\frac{62π}{180})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{62π}{180}−\frac{π}{3})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{2π}{180})=\frac{\sqrt{3}}{2}+\frac{π}{180}≈0.88348.\)
Encontre a aproximação linear para\(f(x)=\cos x \) em\(x=\frac{π}{2}.\)
- Dica
-
\(L(x)=f(a)+f'(a)(x−a)\)
- Resposta
-
\(L(x)=−x+\frac{π}{2}\)
Aproximações lineares podem ser usadas para estimar raízes e potências. No próximo exemplo, encontramos a aproximação linear para\(f(x)=(1+x)^n\) at\(x=0\), que pode ser usada para estimar raízes e potências para números reais próximos\(1\). A mesma ideia pode ser estendida a uma função da forma\(f(x)=(m+x)^n\) para estimar raízes e potências próximas a um número diferente\(m\).
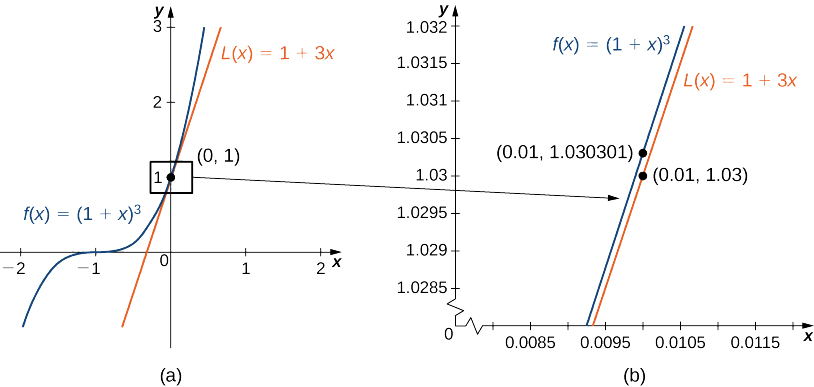
Encontre a aproximação linear de\(f(x)=(1+x)^n\) at\(x=0\). Use essa aproximação para estimar\((1.01)^3.\)
Solução
A aproximação linear em\(x=0\) é dada por
\(L(x)=f(0)+f'(0)(x−0).\)
Porque
\(f(x)=(1+x)^n⇒f(0)=1\)
\(f'(x)=n(1+x)^{n−1}⇒f'(0)=n,\)
a aproximação linear é dada pela Figura\(\PageIndex{4a}\).
\(L(x)=1+n(x−0)=1+nx\)
Podemos fazer uma aproximação\((1.01)^3\) avaliando\(L(0.01)\) quando\(n=3\). Concluímos que
\((1.01)^3=f(1.01)≈L(1.01)=1+3(0.01)=1.03.\)
Encontre a aproximação linear de\(f(x)=(1+x)^4\) at\(x=0\) sem usar o resultado do exemplo anterior.
- Dica
-
\(f'(x)=4(1+x)^3\)
- Resposta
-
\(L(x)=1+4x\)
Diferenciais
Vimos que aproximações lineares podem ser usadas para estimar os valores da função. Eles também podem ser usados para estimar a quantidade em que o valor de uma função muda como resultado de uma pequena alteração na entrada. Para discutir isso de forma mais formal, definimos um conceito relacionado: diferenciais. Os diferenciais nos fornecem uma maneira de estimar a quantidade que uma função muda como resultado de uma pequena alteração nos valores de entrada.
Quando analisamos as derivadas pela primeira vez, usamos a notação de Leibniz\(dy/dx\) para representar a derivada de em\(y\) relação\(x\) a. Embora tenhamos usado as expressões\(dy\) e\(dx\) nessa notação, elas não tinham significado por si só. Aqui vemos um significado para as expressões\(dy\)\(dx\) e. Suponha que\(y=f(x)\) seja uma função diferenciável. \(dx\)Seja uma variável independente que possa ser atribuída a qualquer número real diferente de zero e defina a variável dependente\(dy\) por
\[dy=f'(x)\,dx. \label{diffeq} \]
É importante notar que isso\(dy\) é uma função de ambos\(x\)\(dx\) e. As expressões\(dy\) e\(dx\) são chamadas de diferenciais. Podemos dividir os dois lados da Equação\ ref {diffeq} pela\(dx,\) qual produz
\[\frac{dy}{dx}=f'(x). \label{inteq} \]
Essa é a expressão familiar que usamos para denotar uma derivada. A equação\ ref {inteq} é conhecida como a forma diferencial da Equação\ ref {diffeq}.
Para cada uma das seguintes funções, encontre\(dy\) e avalie quando\(x=3\) e\(dx=0.1.\)
- \(y=x^2+2x\)
- \(y=\cos x \)
Solução
A etapa principal é calcular a derivada. Quando temos isso, podemos obter\(dy\) diretamente.
a. Uma vez que\(f(x)=x^2+2x,\) sabemos e\(f'(x)=2x+2\), portanto,
\(dy=(2x+2)\,dx.\)
Quando\(x=3\) e\(dx=0.1,\)
\(dy=(2⋅3+2)(0.1)=0.8.\)
b. Uma vez que\(f(x)=\cos x , f'(x)=−\sin(x).\) isso nos dá
\(dy=−\sin x \,dx.\)
Quando\(x=3\) e\(dx=0.1,\)
\(dy=−\sin(3)(0.1)=−0.1\sin(3).\)
Para\(y=e^{x^2}\), encontre\(dy\).
- Dica
-
\(dy=f'(x)\,dx\)
- Resposta
-
\(dy=2xe^{x^2}dx\)
Agora conectamos diferenciais a aproximações lineares. Os diferenciais podem ser usados para estimar a mudança no valor de uma função resultante de uma pequena alteração nos valores de entrada. Considere uma função\(f\) que seja diferenciável em alguns pontos\(a\). Suponha que a entrada\(x\) mude em uma pequena quantidade. Estamos interessados em saber o quanto a produção\(y\) muda. Se\(x\) mudar de\(a\) para\(a+dx\), então a mudança em\(x\) é\(dx\) (também indicada\(Δx\)), e a mudança em\(y\) é dada por
\[Δy=f(a+dx)−f(a). \nonumber \]
Em vez de calcular a mudança exata\(y\), no entanto, geralmente é mais fácil aproximar a mudança\(y\) usando uma aproximação linear. \(x\)\(a, f(x)\)Pois near pode ser aproximado pela aproximação linear (Equation\ ref {linearapprox})
\[L(x)=f(a)+f'(a)(x−a). \nonumber \]
Portanto, se\(dx\) for pequeno,
\[f(a+dx)≈L(a+dx)=f(a)+f'(a)(a+dx−a). \nonumber \]
Ou seja,
\[f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx. \nonumber \]
Em outras palavras, a mudança real na função\(f\) if\(x\) aumenta de\(a\) para\(a+dx\) é aproximadamente a diferença entre\(L(a+dx)\) e\(f(a)\), onde\(L(x)\) está a aproximação linear de\(f\) at\(a\). Por definição de\(L(x)\), essa diferença é igual\(f'(a)\,dx\) a. Em resumo,
\[Δy=f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx=dy. \nonumber \]
Portanto, podemos usar o diferencial\(dy=f'(a)\,dx\) para aproximar a mudança em\(y\) se\(x\) aumentar de\(x=a\) para\(x=a+dx\). Podemos ver isso no gráfico a seguir.
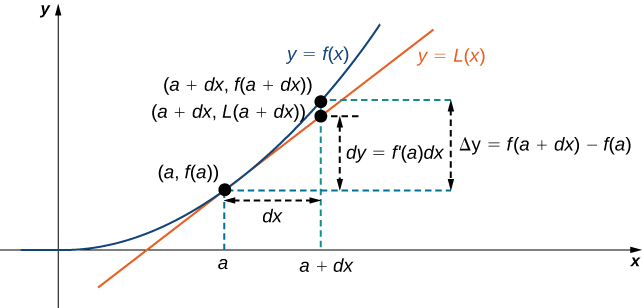
Agora vamos dar uma olhada em como usar diferenciais para aproximar a mudança no valor da função que resulta de uma pequena mudança no valor da entrada. Observe que o cálculo com diferenciais é muito mais simples do que calcular os valores reais das funções e o resultado é muito próximo ao que obteríamos com o cálculo mais exato.
Deixe o\(y=x^2+2x.\) Compute\(Δy\) e\(dy\) at\(x=3\) if\(dx=0.1.\)
Solução
A mudança real no\(y\) if\(x\) muda de\(x=3\) para\(x=3.1\) é dada por
\(Δy=f(3.1)−f(3)=[(3.1)^2+2(3.1)]−[3^2+2(3)]=0.81.\)
A mudança aproximada em\(y\) é dada por\(dy=f'(3)\,dx\). Uma vez\(f'(x)=2x+2,\) que temos
\(dy=f'(3)\,dx=(2(3)+2)(0.1)=0.8.\)
Para\(y=x^2+2x,\) encontrar\(Δy\) e\(dy\)\(x=3\) se\(dx=0.2.\)
- Dica
-
\(dy=f'(3)\,dx, \;Δy=f(3.2)−f(3)\)
- Resposta
-
\(dy=1.6, \; Δy=1.64\)
Calculando a quantidade de erro
Qualquer tipo de medição está sujeito a uma certa quantidade de erro. Em muitas aplicações, determinadas quantidades são calculadas com base em medições. Por exemplo, a área de um círculo é calculada medindo o raio do círculo. Um erro na medição do raio leva a um erro no valor computado da área. Aqui, examinamos esse tipo de erro e estudamos como os diferenciais podem ser usados para estimar o erro.
Considere uma função\(f\) com uma entrada que seja uma quantidade medida. Suponha que o valor exato da quantidade medida seja\(a\), mas o valor medido seja\(a+dx\). Dizemos que o erro de medição é\(dx\) (ou\(Δx\)). Como resultado, ocorre um erro na quantidade calculada\(f(x)\). Esse tipo de erro é conhecido como erro propagado e é dado por
\[Δy=f(a+dx)−f(a). \nonumber \]
Como todas as medições estão sujeitas a algum grau de erro, não sabemos o valor exato de uma quantidade medida, portanto, não podemos calcular exatamente o erro propagado. No entanto, dada uma estimativa da precisão de uma medição, podemos usar diferenciais para aproximar o erro propagado.\(Δy.\) Especificamente, se\(f\) for uma função diferenciável em\(a\), o erro propagado é
\[Δy≈dy=f'(a)\,dx. \nonumber \]
Infelizmente, não sabemos o valor exato.\(a.\) No entanto, podemos usar o valor medido\(a+dx,\) e estimar
\[Δy≈dy≈f'(a+dx)\,dx. \nonumber \]
No próximo exemplo, veremos como os diferenciais podem ser usados para estimar o erro no cálculo do volume de uma caixa se assumirmos que a medição do comprimento lateral é feita com certa precisão.
Suponha que o comprimento lateral de um cubo seja medido em\(5\) cm com uma precisão de\(0.1\) cm.
- Use diferenciais para estimar o erro no volume computado do cubo.
- Calcule o volume do cubo se o comprimento lateral for (i)\(4.9\) cm e (ii)\(5.1\) cm para comparar o erro estimado com o erro potencial real.
Solução
a. A medição do comprimento lateral é precisa dentro de\(±0.1\) cm. Portanto,
\(−0.1≤dx≤0.1.\)
O volume de um cubo é dado por\(V=x^3\), o que leva a
\(dV=3x^2dx.\)
Usando o comprimento lateral medido de\(5\) cm, podemos estimar que
\(−3(5)^2(0.1)≤dV≤3(5)^2(0.1).\)
Portanto,
\(−7.5≤dV≤7.5.\)
b. Se o comprimento do lado for realmente\(4.9\) cm, o volume do cubo será
\(V(4.9)=(4.9)^3=117.649\text{cm}^3.\)
Se o comprimento do lado for realmente\(5.1\) cm, o volume do cubo será
\(V(5.1)=(5.1)^3=132.651\text{cm}^3.\)
Portanto, o volume real do cubo está entre\(117.649\)\(132.651\) e. Como o comprimento do lado é medido em 5 cm, o volume calculado é\(V(5)=5^3=125.\) Portanto, o erro no volume calculado é
\(117.649−125≤ΔV≤132.651−125.\)
Ou seja,
\(−7.351≤ΔV≤7.651.\)
Vemos que o erro estimado\(dV\) está relativamente próximo do erro potencial real no volume calculado.
Estime o erro no volume computado de um cubo se o comprimento do lado for medido em\(6\) cm com uma precisão de\(0.2\) cm.
- Dica
-
\(dV=3x^2dx\)
- Resposta
-
A medição do volume é precisa para dentro\(21.6\,\text{cm}^3\).
O erro de medição\(dx\ (=Δx)\) e o erro propagado\(Δy\) são erros absolutos. Normalmente, estamos interessados no tamanho de um erro em relação ao tamanho da quantidade que está sendo medida ou calculada. Dado um erro absoluto\(Δq\) para uma quantidade específica, definimos o erro relativo como\(\frac{Δq}{q}\), onde\(q\) está o valor real da quantidade. O erro percentual é o erro relativo expresso como uma porcentagem. Por exemplo, se medirmos a altura de uma escada para estar\(63\) em. quando a altura real está\(62\) em., o erro absoluto é de 1 pol. mas o erro relativo é\(\frac{1}{62}=0.016\), ou\(1.6\%\). Em comparação, se medirmos a largura de um pedaço de papelão\(8.25\) em. Quando a largura real está\(8\) em., nosso erro absoluto está\(\frac{1}{4}\) em., enquanto o erro relativo é\(\frac{0.25}{8}=\frac{1}{32}\), ou\(3.1\%.\) Portanto, o erro percentual na medição do papelão é maior, mesmo embora\(0.25\) em. seja menor do que\(1\) em.
Um astronauta usando uma câmera mede o raio da Terra como\(4000\) mi com um erro de\(±80\) mi. Vamos usar diferenciais para estimar o erro relativo e percentual de usar essa medição de raio para calcular o volume da Terra, supondo que o planeta seja uma esfera perfeita.
Solução: Se a medição do raio for precisa para dentro,\(±80,\) temos
\(−80≤dr≤80.\)
Como o volume de uma esfera é dado por\(V=(\frac{4}{3})πr^3,\), temos
\(dV=4πr^2dr.\)
Usando o raio medido de\(4000\) mi, podemos estimar
\(−4π(4000)^2(80)≤dV≤4π(4000)^2(80).\)
Para estimar o erro relativo, considere\(\dfrac{dV}{V}\). Como não sabemos o valor exato do volume\(V\), use o raio\(r=4000\) mi medido para estimar\(V\). Nós obtemos\(V≈(\frac{4}{3})π(4000)^3\). Portanto, o erro relativo satisfaz
\(\frac{−4π(4000)^2(80)}{4π(4000)^3/3}≤\dfrac{dV}{V}≤\frac{4π(4000)^2(80)}{4π(4000)^3/3},\)
o que simplifica para
\(−0.06≤\dfrac{dV}{V}≤0.06.\)
O erro relativo é\(0.06\) e o erro percentual é\(6\%\).
Determine o erro percentual se o raio da Terra for medido em\(3950\) mi com um erro de\(±100\) mi.
- Dica
-
Use o fato de que\(dV=4πr^2dr\) para encontrar\(dV/V\).
- Resposta
-
\(7.6\%\)
Conceitos chave
- Uma função diferenciável\(y=f(x)\) pode ser aproximada em\(a\) pela função linear
\(L(x)=f(a)+f'(a)(x−a).\)
- Para uma função\(y=f(x)\), se\(x\) mudar de\(a\) para\(a+dx\), então
\(dy=f'(x)\,dx\)
é uma aproximação para a mudança em\(y\). A mudança real em\(y\) é
\(Δy=f(a+dx)−f(a).\)
- Um erro de medição\(dx\) pode levar a um erro em uma quantidade calculada\(f(x)\). O erro na quantidade calculada é conhecido como erro propagado. O erro propagado pode ser estimado por
\(dy≈f'(x)\,dx.\)
- Para estimar o erro relativo de uma quantidade específica\(q\), estimamos\(\frac{Δq}{q}\).
Equações chave
- Aproximação linear
\(L(x)=f(a)+f'(a)(x−a)\)
- Um diferencial
\(dy=f'(x)\,dx\)
Glossário
- diferencial
- o diferencial\(dx\) é uma variável independente à qual pode ser atribuído qualquer número real diferente de zero; o diferencial\(dy\) é definido como\(dy=f'(x)\,dx\)
- forma diferencial
- dada uma função diferenciável,\(y=f'(x),\) a equação\(dy=f'(x)\,dx\) é a forma diferencial da derivada de em\(y\) relação a\(x\)
- aproximação linear
- a função linear\(L(x)=f(a)+f'(a)(x−a)\) é a aproximação linear de\(f\) em\(x=a\)
- erro percentual
- o erro relativo expresso em porcentagem
- erro propagado
- o erro que resulta em uma quantidade calculada\(f(x)\) resultante de um erro de medição\(dx\)
- erro relativo
- dado um erro absoluto\(Δq\) para uma quantidade específica,\(\frac{Δq}{q}\) é o erro relativo.
- aproximação da linha tangente (linearização)
- como a aproximação linear de\(f\) at\(x=a\) é definida usando a equação da reta tangente, a aproximação linear de\(f\) at também\(x=a\) é conhecida como aproximação da reta tangente a\(f\) at\(x=a\)


