3.8: Diferenciação implícita
- Page ID
- 188464
- Encontre a derivada de uma função complicada usando a diferenciação implícita.
- Use a diferenciação implícita para determinar a equação de uma reta tangente.
Já estudamos como encontrar equações de retas tangentes a funções e a taxa de variação de uma função em um ponto específico. Em todos esses casos, tínhamos a equação explícita para a função e diferenciamos essas funções explicitamente. Suponha, em vez disso, que desejemos determinar a equação de uma reta tangente a uma curva arbitrária ou a taxa de variação de uma curva arbitrária em um ponto. Nesta seção, resolvemos esses problemas encontrando as derivadas de funções que definem\(y\) implicitamente em termos de\(x\).
Diferenciação implícita
Na maioria das discussões de matemática, se a variável dependente\(y\) for uma função da variável independente\(x\), expressamos y em termos de\(x\). Se for esse o caso, dizemos que\(y\) é uma função explícita de\(x\). Por exemplo, quando escrevemos a equação\(y=x^2+1\), estamos definindo y explicitamente em termos de\(x\). Por outro lado, se a relação entre a função\(y\) e a variável\(x\) é expressa por uma equação onde não\(y\) é expressa inteiramente em termos de\(x\), dizemos que a equação define\(y\) implicitamente em termos de\(x\). Por exemplo, a equação\(y−x^2=1\) define a função\(y=x^2+1\) implicitamente.
A diferenciação implícita nos permite encontrar inclinações de tangentes a curvas que claramente não são funções (elas falham no teste da linha vertical). Estamos usando a ideia de que partes de\(y\) são funções que satisfazem a equação dada, mas que y não é realmente uma função de\(x\).
Em geral, uma equação define uma função implicitamente se a função satisfizer essa equação. Uma equação pode definir muitas funções diferentes implicitamente. Por exemplo, as funções
\[y=\sqrt{25−x^2}\nonumber \]
e
\[y=\begin{cases}\sqrt{25−x^2}, & \text{if }−5≤x<0\\ −\sqrt{25−x^2}, & \text{if }0≤x≤5\end{cases}\nonumber \]
que são ilustradas na Figura\(\PageIndex{1}\), são apenas duas das muitas funções definidas implicitamente pela equação\(x^2+y^2=25\).
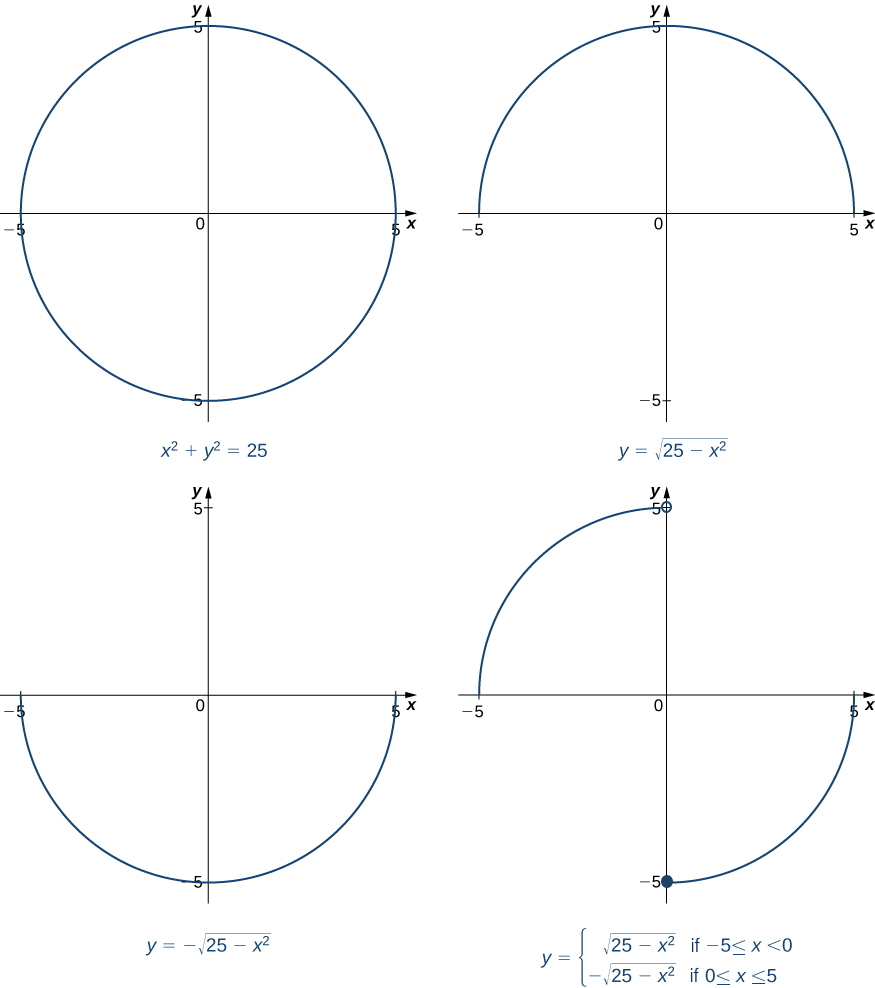
Se quisermos encontrar a inclinação da reta tangente ao gráfico de\(x^2+y^2=25\) no ponto\((3,4)\), poderíamos calcular a derivada da função\(y=\sqrt{25−x^2}\) em\(x=3\). Por outro lado, se quisermos a inclinação da reta tangente no ponto\((3,−4)\), poderíamos usar a derivada de\(y=−\sqrt{25−x^2}\). No entanto, nem sempre é fácil resolver uma função definida implicitamente por uma equação. Felizmente, a técnica de diferenciação implícita nos permite encontrar a derivada de uma função definida implicitamente sem nunca resolver a função explicitamente. O processo de descoberta\(\dfrac{dy}{dx}\) usando diferenciação implícita é descrito na seguinte estratégia de resolução de problemas.
Para realizar a diferenciação implícita em uma equação que define uma função\(y\) implicitamente em termos de uma variável\(x\), use as seguintes etapas:
- Pegue a derivada de ambos os lados da equação. Lembre-se de que isso\(y\) é uma função do\(x\). Consequentemente, enquanto\[\dfrac{d}{dx}(\sin x)=\cos x\nonumber \] e\[\dfrac{d}{dx}(\sin y)=\cos y\cdot\dfrac{dy}{dx}\nonumber \] porque devemos usar a regra da cadeia para diferenciar em\(\sin y\) relação\(x\) a.
- Reescreva a equação para que todos os termos que contêm\(dy/dx\) estejam à esquerda e todos os termos que não contêm\(dy/dx\) estejam à direita.
- Fale\(dy/dx\) à esquerda.
- Resolva isso\(dy/dx\) dividindo os dois lados da equação por uma expressão algébrica apropriada.
Supondo que\(y\) seja definido implicitamente pela equação\(x^2+y^2=25\), encontre\(\dfrac{dy}{dx}\).
Solução
Siga as etapas da estratégia de solução de problemas.
| \(\dfrac{d}{dx}(x^2+y^2)=\dfrac{d}{dx}(25)\) | Etapa 1. Diferencie os dois lados da equação. |
| \(\dfrac{d}{dx}(x^2)+\dfrac{d}{dx}(y^2)=0\) | Etapa 1.1. Use a regra de soma à esquerda. À direita\(\dfrac{d}{dx}(25)=0\). |
| \(2x+2y\dfrac{dy}{dx}=0\) | Etapa 1.2. Pegue os derivados, então\(\dfrac{d}{dx}(x^2)=2x\)\(\dfrac{d}{dx}(y^2)=2y\dfrac{dy}{dx}\) e. |
| \(2y\dfrac{dy}{dx}=−2x\) | Etapa 2. Mantenha os termos com\(\dfrac{dy}{dx}\) à esquerda. Mova os termos restantes para a direita. |
| \(\dfrac{dy}{dx}=−\dfrac{x}{y}\) | Etapa 4. Divida os dois lados da equação por\(2y\). (A etapa 3 não se aplica nesse caso.) |
Análise
Observe que a expressão resultante para\(\dfrac{dy}{dx}\) é em termos da variável independente\(x\) e da variável dependente\(y\). Embora em alguns casos seja possível expressar\(x\) apenas\(\dfrac{dy}{dx}\) em termos de, geralmente não é possível fazê-lo.
Supondo que\(y\) seja definido implicitamente pela equação\(x^3\sin y+y=4x+3\), encontre\(\dfrac{dy}{dx}\).
Solução
| \(\dfrac{d}{dx}(x^3\sin y+y)=\dfrac{d}{dx}(4x+3)\) | Etapa 1: diferencie os dois lados da equação. |
| \(\dfrac{d}{dx}(x^3\sin y)+\dfrac{d}{dx}(y)=4\) | Etapa 1.1: aplique a regra de soma à esquerda. À direita,\(\dfrac{d}{dx}(4x+3)=4\). |
| \(\left(\dfrac{d}{dx}(x^3)⋅\sin y+\dfrac{d}{dx}(\sin y)⋅x^3\right)+\dfrac{dy}{dx}=4\) | Etapa 1.2: Use a regra do produto para encontrar\(\dfrac{d}{dx}(x^3\sin y)\). Observe isso\(\dfrac{d}{dx}(y)=\dfrac{dy}{dx}\). |
| \(3x^2\sin y+(\cos y\dfrac{dy}{dx})⋅x^3+\dfrac{dy}{dx}=4\) | Etapa 1.3: Nós sabemos\(\dfrac{d}{dx}(x^3)=3x^2\). Use a regra da cadeia para obter\(\dfrac{d}{dx}(\sin y)=\cos y\dfrac{dy}{dx}\). |
| \(x^3\cos y\dfrac{dy}{dx}+\dfrac{dy}{dx}=4−3x^2\sin y\) | Etapa 2: mantenha todos os termos\(\dfrac{dy}{dx}\) contidos à esquerda. Mova todos os outros termos para a direita. |
| \(\dfrac{dy}{dx}(x^3\cos y+1)=4−3x^2\sin y\) | Etapa 3:\(\dfrac{dy}{dx}\) fatore à esquerda. |
| \(\dfrac{dy}{dx}=\dfrac{4−3x^2\sin y}{x^3\cos y+1}\) | Etapa 4: resolva\(\dfrac{dy}{dx}\) por dividindo os dois lados da equação por\(x^3\cos y+1\). |
Descubra\(\dfrac{d^2y}{dx^2}\) se\(x^2+y^2=25\).
Solução
No exemplo\(\PageIndex{1}\), mostramos isso\(\dfrac{dy}{dx}=−\dfrac{x}{y}\). Podemos pegar a derivada de ambos os lados dessa equação para encontrar\(\dfrac{d^2y}{dx^2}\).
\ (\ begin {align*}\ dfrac {d^2y} {dx^2} &=\ dfrac {d} {dy}\ left (−\ dfrac {x} {y}\ right) &\ text {Diferencie os dois lados de}\ dfrac {dy} {dx} =−\ dfrac {x} {y}.\\ [4pt]
−\ dfrac {\ left (1⋅y−x\ dfrac {dy} {dx}\ right)} {y^2} & &\ text {Use a regra do quociente para encontrar}\ dfrac {d} {dy}\ left (−\ dfrac {x} {y} \ right).\\ [4pt]
&=\ dfrac {−y+x\ dfrac {dy} {dx}} {y^2} & &\ text {Simplifique.}\\ [4pt]
&=\ dfrac {−y+x\ left (−\ dfrac {x} {y}\ right)} {y^2} & &\ text {Substituto} dfrac {dy} {dx} =−\ dfrac {x} {y}.\\ [4pt]
&=\ dfrac {−y^2−x^2} {y^3} & &\ text {Simplificar.} \ end {align*}\)
Neste ponto, encontramos uma expressão para\(\dfrac{d^2y}{dx^2}\). Se escolhermos, podemos simplificar ainda mais a expressão lembrando isso\(x^2+y^2=25\) e fazendo essa substituição no numerador para obter\(\dfrac{d^2y}{dx^2}=−\dfrac{25}{y^3}\).
Encontre\(\dfrac{dy}{dx}\) para\(y\) definido implicitamente pela equação\(4x^5+\tan y=y^2+5x\).
- Dica
-
Siga a estratégia de resolução de problemas, lembrando-se de aplicar a regra da cadeia para diferenciar\(\tan y\)\(y^2\) e.
- Responda
-
\[\dfrac{dy}{dx}=\dfrac{5−20x^4}{\sec^2y−2y} \nonumber \]
Encontrando linhas tangentes implicitamente
Agora que vimos a técnica de diferenciação implícita, podemos aplicá-la ao problema de encontrar equações de retas tangentes a curvas descritas por equações.
Encontre a equação da reta tangente à curva\(x^2+y^2=25\) no ponto\((3,−4)\).
Solução
Embora pudéssemos encontrar essa equação sem usar diferenciação implícita, usar esse método torna isso muito mais fácil. No exemplo\(\PageIndex{1}\), encontramos\(\dfrac{dy}{dx}=−\dfrac{x}{y}\).
A inclinação da reta tangente é encontrada\((3,−4)\) substituindo-a por essa expressão. Consequentemente, a inclinação da reta tangente é\(\dfrac{dy}{dx}\Big|_{(3,−4)}=−\dfrac{3}{−4}=\dfrac{3}{4}\).
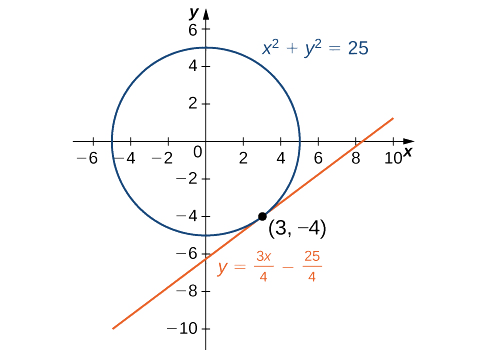
Usando o ponto\((3,−4)\) e a inclinação\(\dfrac{3}{4}\) na equação ponto-inclinação da reta, obtemos a equação\(y=\dfrac{3}{4}x−\dfrac{25}{4}\) (Figura\(\PageIndex{2}\)).
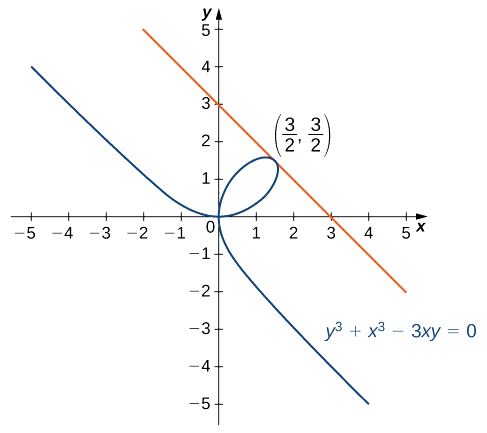
Encontre a equação da reta tangente ao gráfico de\(y^3+x^3−3xy=0\) no ponto\(\left(\frac{3}{2},\frac{3}{2}\right)\) (Figura\(\PageIndex{3}\)). Essa curva é conhecida como fólio (ou folha) de Descartes.
Solução
Comece encontrando\(\dfrac{dy}{dx}\).
\(\dfrac{d}{dx}\big(y^3+x^3−3xy\big)=\dfrac{d}{dx}\big(0\big)\)
\(3y^2\dfrac{dy}{dx}+3x^2−\left(3y+3x\dfrac{dy}{dx}\right)=0\)
\(3y^2\dfrac{dy}{dx}+3x^2−3y-3x\dfrac{dy}{dx}=0\)
\(\left(3y^2-3x\right)\dfrac{dy}{dx}=3y-3x^2\)
\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\).
Em seguida,\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\) substitua\(\left(\frac{3}{2},\frac{3}{2}\right)\) em para encontrar a inclinação da reta tangente:
\(\dfrac{dy}{dx}\Bigg|_{\left(\frac{3}{2},\frac{3}{2}\right)}=−1\).
Finalmente, substitua a equação ponto-inclinação da linha para obter
\(y=−x+3\).
Em um videogame simples, um foguete viaja em uma órbita elíptica cujo caminho é descrito pela equação\(4x^2+25y^2=100\). O foguete pode disparar mísseis ao longo de linhas tangentes ao seu caminho. O objetivo do jogo é destruir um asteróide que se aproxima viajando ao longo do\(x\) eixo positivo em direção a\((0,0)\). Se o foguete disparar um míssil quando estiver localizado\(\left(3,\frac{8}{5}\right)\), onde ele cruzará o\(x\) eixo -?
Solução
Para resolver esse problema, devemos determinar onde a reta tangente ao gráfico de
\(4x^2+25y^2=100\)at\(\left(3,\frac{8}{5}\right)\) cruza o\(x\) eixo y. Comece encontrando\(\dfrac{dy}{dx}\) implicitamente.
Diferenciando, temos
\(8x+50y\dfrac{dy}{dx}=0.\)
Resolvendo para\(\dfrac{dy}{dx}\),
nós temos
\(\dfrac{dy}{dx}=−\dfrac{4x}{25y}\).
A inclinação da reta tangente é\(\dfrac{dy}{dx}\Bigg|_{\left(3,\frac{8}{5}\right)}=−\dfrac{3}{10}\). A equação da reta tangente é\(y=−\dfrac{3}{10}x+\dfrac{5}{2}\). Para determinar onde a linha cruza o\(x\) eixo -, resolva\(0=−\dfrac{3}{10}x+\dfrac{5}{2}\). A solução é\(x=\dfrac{25}{3}\). O míssil cruza o\(x\) eixo -no ponto\(\left(\frac{25}{3},0\right)\).
Encontre a equação da reta tangente à hipérbole\(x^2−y^2=16\) no ponto\((5,3)\).
- Dica
-
\(\dfrac{dy}{dx}=\dfrac{x}{y}\)
- Responda
-
\(y=\dfrac{5}{3}x−\dfrac{16}{3}\)
Conceitos-chave
- Usamos a diferenciação implícita para encontrar derivadas de funções definidas implicitamente (funções definidas por equações).
- Usando a diferenciação implícita, podemos encontrar a equação de uma reta tangente ao gráfico de uma curva.
Glossário
- diferenciação implícita
- é uma técnica de computação\(\dfrac{dy}{dx}\) para uma função definida por uma equação, realizada diferenciando os dois lados da equação (lembrando de tratar a variável\(y\) como uma função) e resolvendo\(\dfrac{dy}{dx}\)


