3.7E: Exercícios para a Seção 3.7

Last updated
Save as PDF

Page ID: 188428

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 4, use o gráfico$y=f(x)$ de

a. esboce o gráfico de$y=f^{−1}(x)$, e

b. use a parte a. para estimar$\big(f^{−1}\big)′(1)$.

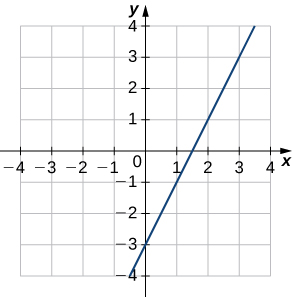
$Uma linha reta passando por (0, −3) e (3, 3).$

$Uma linha curva começando em (−2, 0) e passando por (−1, 1) e (2, 2).$

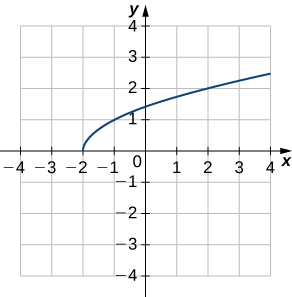
Responda

uma.

$alt$

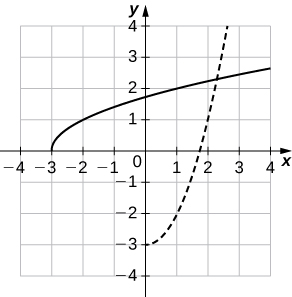
b.$(f^{−1})′(1)\approx 2$

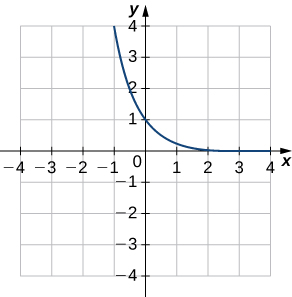
$Uma linha curva começando em (4, 0) e passando por (0, 1) e (−1, 4).$

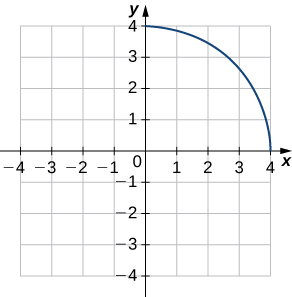
$Um quarto de círculo começando em (0, 4) e terminando em (4, 0).$

Responda

uma.

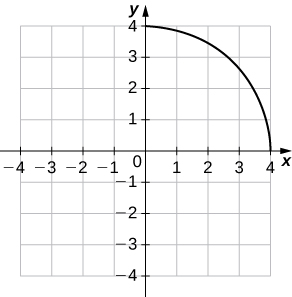
$Um quarto de círculo começando em (0, 4) e terminando em (4, 0).$

b.$(f^{−1})′(1)\approx −1/\sqrt{3}$

Para os exercícios 5 a 8, use a função dada$y=f(x)$ para encontrar

a.$\dfrac{df}{dx}$ em$x=a$ e

$x=f^{−1}(y)$b.

c. Em seguida, use a parte b. para encontrar$\dfrac{df^{−1}}{dy}$ em$y=f(a).$

5)$f(x)=6x−1,\; x=−2$

6)$f(x)=2x^3−3,\; x=1$

Responda: a.$\dfrac{df}{dx} = 6$
b.$x=f^{−1}(y)=\left(\dfrac{y+3}{2}\right)^{1/3}$
c.$\dfrac{df^{−1}}{dy} = \frac{1}{6}$

7)$f(x)=9−x^2,\; 0≤x≤3,x=2$

8)$f(x)=\sin x,\; x=0$

Responda: a.$\dfrac{df}{dx} = 1$
b.$x=f^{−1}(y)=\sin^{−1}y$
c.$\dfrac{df^{−1}}{dy} = 1$

Para cada função nos exercícios 9 a 14, encontre$\big(f^{−1}\big)′(a)$.

9)$f(x)=x^2+3x+2,\; x≥−1,\; a=2$

10$f(x)=x^3+2x+3,\; a=0$

Responda: $\big(f^{−1}\big)′(1) = \frac{1}{5}$

11)$f(x)=x+\sqrt{x},\; a=2$

12)$f(x)=x−\frac{2}{x},\; x<0,\; a=1$

Responda: $\big(f^{−1}\big)′(1) = \frac{1}{3}$

13)$f(x)=x+\sin x,\; a=0$

14)$f(x)=\tan x+3x^2,\; a=0$

Responda: $\big(f^{−1}\big)′(0) = 1$

Para cada função$y=f(x)$, dada nos exercícios 15 a 19,

a. encontre a inclinação da reta tangente à sua função inversa$f^{−1}$ no ponto indicado$P$, e

b. encontre a equação da reta tangente ao gráfico de$f^{−1}$ no ponto indicado.

15)$f(x)=\dfrac{4}{1+x^2},\quad P(2,1)$

16)$f(x)=\sqrt{x−4},\quad P(2,8)$

Responda: a.$4$
b.$y=4x$

17)$f(x)=(x^3+1)^4,\quad P(16,1)$

18)$f(x)=−x^3−x+2,\quad P(−8,2)$

Responda: a.$−\frac{1}{96}$
b.$y=−\frac{1}{13}x+\frac{18}{13}$

19)$f(x)=x^5+3x^3−4x−8,\quad P(−8,1)$

Nos exercícios 20 a 29, encontre$\dfrac{dy}{dx}$ a função dada.

20)$y=\sin^{−1}(x^2)$

Responda: $\dfrac{dy}{dx} = \dfrac{2x}{\sqrt{1−x^4}}$

21)$y=\cos^{−1}\left(\sqrt{x}\right)$

22)$y=\sec^{−1}\left(\frac{1}{x}\right)$

Responda: $\dfrac{dy}{dx} = \dfrac{−1}{\sqrt{1−x^2}}$

23)$y=\sqrt{\csc^{−1}x}$

24)$y=(1+\tan^{−1}x)^3$

Responda: $\dfrac{dy}{dx} = \dfrac{3(1+\tan^{−1}x)^2}{1+x^2}$

25)$y=\cos^{−1}(2x)⋅\sin^{−1}(2x)$

26)$y=\dfrac{1}{\tan^{−1}(x)}$

Responda: $\dfrac{dy}{dx} = \dfrac{−1}{(1+x^2)(\tan^{−1}x)^2}$

27)$y=\sec^{−1}(−x)$

28)$y=\cot^{−1}\sqrt{4−x^2}$

Responda: $\dfrac{dy}{dx} = \dfrac{x}{(5−x^2)\sqrt{4−x^2}}$

29)$y=x⋅\csc^{−1}x$

Nos exercícios 30 a 35, use os valores fornecidos para encontrar$\big(f^{−1}\big)′(a)$.

30)$f(π)=0,f'(π)=−1,a=0$

Responda: $\big(f^{−1}\big)′(0) = −1$

31)$f(6)=2,\; f′(6)=\frac{1}{3},\; a=2$

32)$f(\frac{1}{3})=−8,\; f'(\frac{1}{3})=2,\; a=−8$

Responda: $\big(f^{−1}\big)′(-8) = \frac{1}{2}$

33)$f(\sqrt{3})=\frac{1}{2},f'(\sqrt{3})=\frac{2}{3},a=\frac{1}{2}$

34)$f(1)=−3,\; f'(1)=10,\; a=−3$

Responda: $\big(f^{−1}\big)′(-3) =\frac{1}{10}$

(35)$f(1)=0,\; f'(1)=−2,\; a=0$

36) [T] A posição de um disco de hóquei em movimento após$t$ segundos é$s(t)=tan^{−1}t$ onde$s$ está em metros.

a. Encontre a velocidade do disco de hóquei a qualquer momento$t$.

b. Encontre a aceleração do disco a qualquer momento$t$.

c. Avalie as partes a. e b. por$t=2,\, 4$ e$6$ segundos.

d. Que conclusão pode ser extraída dos resultados em c.?

Responda

a.$v(t)=\dfrac{1}{1+t^2}$
b.$a(t)=\dfrac{−2t}{(1+t^2)^2}$
c. (a)$0.2,\, 0.06,\, 0.03$; (b)$−0.16,\, −0.028,\, −0.0088$

d. O disco de hóquei está desacelerando/desacelerando em 2, 4 e 6 segundos.

Solução:

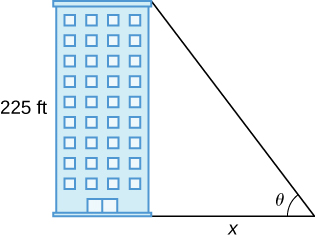
37) [T] Um prédio com 225 pés de altura projeta uma sombra de vários comprimentos à$x$ medida que o dia passa. Um ângulo de elevação$θ$ é formado por linhas da parte superior e inferior do edifício até a ponta da sombra, como pode ser visto na figura a seguir. Encontre a taxa de variação do ângulo de elevação$\frac{dθ}{dx}$ quando$x=272$ pés.

$Um edifício é mostrado com 225 pés de altura. Um triângulo é feito com a altura do edifício como o lado oposto do ângulo θ. O lado adjacente tem comprimento x.$

38) [T] Um poste tem 75 pés de altura. Um ângulo$θ$ é formado quando fios de vários comprimentos de$x$ pés são presos do solo ao topo do poste, conforme mostrado na figura a seguir. Encontre a taxa de variação do ângulo$\frac{dθ}{dx}$ quando um fio de 90 pés de comprimento é conectado.

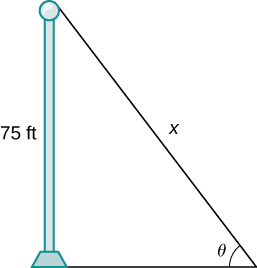
$Um mastro de bandeira é mostrado com altura de 75 pés. Um triângulo é feito com a altura do mastro da bandeira como o lado oposto do ângulo θ. A hipotenusa tem comprimento x.$

Responda: $−0.0168$radianos por pé

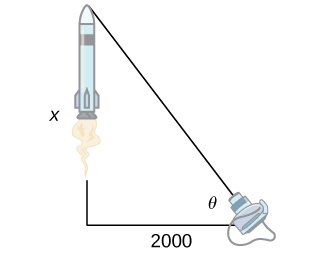
39) [T] Uma câmera de televisão no nível do solo está a 2000 pés de distância da plataforma de lançamento de um foguete espacial que está programado para decolar verticalmente, como pode ser visto na figura a seguir. O ângulo de elevação da câmera pode ser encontrado por$θ=\tan^{−1}\left(\frac{x}{2000}\right)$, onde$x$ está a altura do foguete. Encontre a taxa de variação do ângulo de elevação após o lançamento quando a câmera e o foguete estiverem a 5000 pés de distância.

$Um foguete é mostrado no ar com a distância de seu nariz até o solo sendo x. Um triângulo é feito com a altura do foguete como o lado oposto do ângulo θ. O lado adjacente tem 2000 de comprimento.$

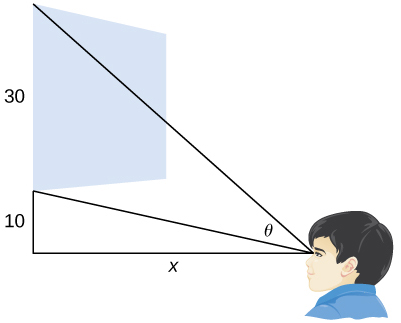
40) [T] Um cinema local com uma tela de 30 pés de altura que está 10 pés acima do nível dos olhos de uma pessoa quando sentada tem um ângulo de visão$θ$ (em radianos) dado por$θ=\cot^{−1}\frac{x}{40}−\cot^{−1}\frac{x}{10}$,

onde$x$ está a distância em pés da tela de cinema em que a pessoa está sentada, conforme mostrado na figura a seguir.

$Uma pessoa é mostrada com um triângulo reto saindo do olho (o ângulo reto está no lado oposto do olho), com altura 10 e base x. Há uma linha traçada do olho até o topo da tela, que forma um ângulo θ com a hipotenusa do triângulo. A tela tem uma altura de 30.$

a. Encontre$\dfrac{dθ}{dx}$.

b. Avalie$\dfrac{dθ}{dx}$ para$x=5,\,10,\,15,$$20$ e.

c. Interprete os resultados na parte b.

d. Avalie$\dfrac{dθ}{dx}$ para$x=25,\,30,\,35$,$40$ e.

e. Interprete os resultados na parte d. A que distância a pessoa$x$ deve ficar para maximizar seu ângulo de visão?

Responda: a.$\dfrac{dθ}{dx}=\dfrac{10}{100+x^2}−\dfrac{40}{1600+x^2}$
b.$\frac{18}{325},\,\frac{9}{340},\,\frac{42}{4745},\,0$
c. À medida que uma pessoa se afasta da tela, o ângulo de visão aumenta, o que implica que, à medida que ela se afasta, sua visão na tela aumenta. d.$−\frac{54}{12905},\,−\frac{3}{500},\,−\frac{198}{29945},\,−\frac{9}{1360}$
e. À medida que a pessoa se move além de 20 pés da tela, o ângulo de visão está diminuindo. A distância ideal que a pessoa deve ficar para maximizar o ângulo de visão é de 20 pés.