3.7: Derivadas de funções inversas
- Page ID
- 188412
- Calcule a derivada de uma função inversa.
- Reconheça as derivadas das funções trigonométricas inversas padrão.
Nesta seção, exploramos a relação entre a derivada de uma função e a derivada de seu inverso. Para funções cujas derivadas já conhecemos, podemos usar essa relação para encontrar derivadas de inversas sem precisar usar a definição de limite da derivada. Em particular, aplicaremos a fórmula para derivadas de funções inversas a funções trigonométricas. Essa fórmula também pode ser usada para estender a regra de potência para expoentes racionais.
A derivada de uma função inversa
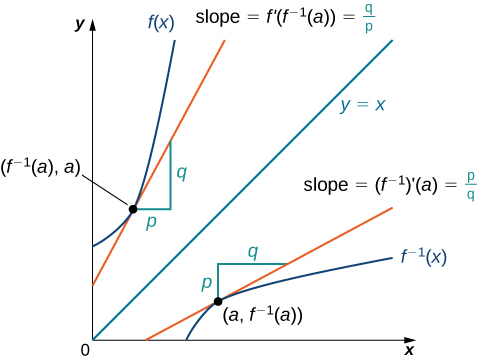
Começamos considerando uma função e seu inverso. Se\(f(x)\) for invertível e diferenciável, parece razoável que o inverso de também\(f(x)\) seja diferenciável. A figura\(\PageIndex{1}\) mostra a relação entre uma função\(f(x)\) e seu inverso\(f^{−1}(x)\). Veja o ponto\(\left(a,\,f^{−1}(a)\right)\) no gráfico de\(f^{−1}(x)\) ter uma reta tangente com uma inclinação de
\[\big(f^{−1}\big)′(a)=\dfrac{p}{q}. \nonumber \]
Este ponto corresponde a um ponto\(\left(f^{−1}(a),\,a\right)\) no gráfico de\(f(x)\) ter uma reta tangente com uma inclinação de
\[f′\big(f^{−1}(a)\big)=\dfrac{q}{p}. \nonumber \]
Assim, se\(f^{−1}(x)\) é diferenciável em\(a\), então deve ser o caso de que
\(\big(f^{−1}\big)′(a)=\dfrac{1}{f′\big(f^{−1}(a)\big)}\).
Também podemos derivar a fórmula para a derivada do inverso lembrando isso primeiro\(x=f\big(f^{−1}(x)\big)\). Então, ao diferenciar os dois lados dessa equação (usando a regra da cadeia à direita), obtemos
\(1=f′\big(f^{−1}(x)\big)\big(f^{−1}\big)′(x))\).
Resolvendo para\(\big(f^{−1}\big)′(x)\), obtemos
\(\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}\).
Resumimos esse resultado no seguinte teorema.
\(f(x)\)Seja uma função que seja ao mesmo tempo invertível e diferenciável. \(y=f^{−1}(x)\)Seja o inverso de\(f(x)\). Para todos os\(x\) satisfatórios\(f′\big(f^{−1}(x)\big)≠0\),
\[\dfrac{dy}{dx}=\dfrac{d}{dx}\big(f^{−1}(x)\big)=\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}.\label{inverse1} \]
Alternativamente, se\(y=g(x)\) for o inverso de\(f(x)\), então
\[g'(x)=\dfrac{1}{f′\big(g(x)\big)}. \label{inverse2} \]
Use o teorema da função inversa para encontrar a derivada de\(g(x)=\dfrac{x+2}{x}\). Compare a derivada resultante com a obtida pela diferenciação direta da função.
Solução
O inverso de\(g(x)=\dfrac{x+2}{x}\) é\(f(x)=\dfrac{2}{x−1}\).
Usaremos a Equação\ ref {inverse2} e começaremos encontrando\(f′(x)\). Assim,
\[f′(x)=\dfrac{−2}{(x−1)^2} \nonumber \]
e
\[f′\big(g(x)\big)=\dfrac{−2}{(g(x)−1)^2}=\dfrac{−2}{\left(\dfrac{x+2}{x}−1\right)^2}=−\dfrac{x^2}{2}. \nonumber \]
Finalmente,
\[g′(x)=\dfrac{1}{f′\big(g(x)\big)}=−\dfrac{2}{x^2}. \nonumber \]
Podemos verificar se esta é a derivada correta aplicando a regra do quociente\(g(x)\) para obter
\[g′(x)=−\dfrac{2}{x^2}. \nonumber \]
Use o teorema da função inversa para encontrar a derivada de\(g(x)=\dfrac{1}{x+2}\). Compare o resultado obtido pela diferenciação\(g(x)\) direta.
- Dica
-
Use o exemplo anterior como guia.
- Responda
-
\(g′(x)=−\dfrac{1}{(x+2)^2}\)
Use o teorema da função inversa para encontrar a derivada de\(g(x)=\sqrt[3]{x}\).
Solução
A função\(g(x)=\sqrt[3]{x}\) é o inverso da função\(f(x)=x^3\). Desde então\(g′(x)=\dfrac{1}{f′\big(g(x)\big)}\), comece encontrando\(f′(x)\). Assim,
\[f′(x)=3x^2\nonumber \]
e
\[f′\big(g(x)\big)=3\big(\sqrt[3]{x}\big)^2=3x^{2/3}\nonumber \]
Finalmente,
\[g′(x)=\dfrac{1}{3x^{2/3}}.\nonumber \]
Se fôssemos nos diferenciar\(g(x)\) diretamente, usando a regra do poder, primeiro reescreveríamos\(g(x)=\sqrt[3]{x}\) como um poder de\(x\) obter,
\[g(x) = x^{1/3}\nonumber \]
Em seguida, diferenciaríamos usando a regra de potência para obter
\[g'(x) =\tfrac{1}{3}x^{−2/3} = \dfrac{1}{3x^{2/3}}.\nonumber \]
Encontre a derivada de\(g(x)=\sqrt[5]{x}\) aplicando o teorema da função inversa.
- Dica
-
\(g(x)\)é o inverso de\(f(x)=x^5\).
- Responda
-
\(g(x)=\frac{1}{5}x^{−4/5}\)
No exemplo anterior, vemos que podemos usar o teorema da função inversa para estender a regra da potência aos expoentes da forma\(\dfrac{1}{n}\), onde\(n\) está um número inteiro positivo. Essa extensão, em última análise\(x^q\), nos permitirá diferenciar onde\(q\) está qualquer número racional.
A regra da potência pode ser estendida aos expoentes racionais. Ou seja, se\(n\) for um número inteiro positivo, então
\[\dfrac{d}{dx}\big(x^{1/n}\big)=\dfrac{1}{n} x^{(1/n)−1}. \nonumber \]
Além disso, se\(n\) for um número inteiro positivo e\(m\) for um inteiro arbitrário, então
\[\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}. \nonumber \]
A função\(g(x)=x^{1/n}\) é o inverso da função\(f(x)=x^n\). Desde então\(g′(x)=\dfrac{1}{f′\big(g(x)\big)}\), comece encontrando\(f′(x)\). Assim,
\(f′(x)=nx^{n−1}\)\(f′\big(g(x)\big)=n\big(x^{1/n}\big)^{n−1}=nx^{(n−1)/n}\)e.
Finalmente,
\(g′(x)=\dfrac{1}{nx^{(n−1)/n}}=\dfrac{1}{n}x^{(1−n)/n}=\dfrac{1}{n}x^{(1/n)−1}\).
Para diferenciar,\(x^{m/n}\) devemos reescrevê-la como\((x^{1/n})^m\) e aplicar a regra da cadeia. Assim,
\[\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{d}{dx}\big((x^{1/n}\big)^m)=m\big(x^{1/n}\big)^{m−1}⋅\dfrac{1}{n}x^{(1/n)−1}=\dfrac{m}{n}x^{(m/n)−1}. \nonumber \]
□
Encontre a equação da reta tangente ao gráfico de\(y=x^{2/3}\) at\(x=8\).
Solução
Primeiro, encontre\(\dfrac{dy}{dx}\) e avalie em\(x=8\). Desde
\[\dfrac{dy}{dx}=\frac{2}{3}x^{−1/3} \nonumber \]
e
\[\dfrac{dy}{dx}\Bigg|_{x=8}=\frac{1}{3}\nonumber \]
a inclinação da reta tangente ao gráfico em\(x=8\) é\(\frac{1}{3}\).
\(x=8\)Substituindo a função original, obtemos\(y=4\). Assim, a reta tangente passa pelo ponto\((8,4)\). Substituindo uma reta na fórmula ponto-inclinação, obtemos a reta tangente
\[y=\tfrac{1}{3}x+\tfrac{4}{3}. \nonumber \]
Encontre a derivada de\(s(t)=\sqrt{2t+1}\).
- Dica
-
Use a regra da cadeia.
- Responda
-
\(s′(t)=(2t+1)^{−1/2}\)
Derivadas de funções trigonométricas inversas
Agora voltamos nossa atenção para encontrar derivadas de funções trigonométricas inversas. Essas derivadas serão inestimáveis no estudo da integração posteriormente neste texto. As derivadas de funções trigonométricas inversas são bastante surpreendentes, pois suas derivadas são, na verdade, funções algébricas. Anteriormente, derivadas de funções algébricas provaram ser funções algébricas e derivadas de funções trigonométricas demonstraram ser funções trigonométricas. Aqui, pela primeira vez, vemos que a derivada de uma função não precisa ser do mesmo tipo da função original.
Use o teorema da função inversa para encontrar a derivada de\(g(x)=\sin^{−1}x\).
Solução
Como for\(x\) no intervalo\(\left[−\frac{π}{2},\frac{π}{2}\right],f(x)=\sin x\) é o inverso de\(g(x)=\sin^{−1}x\), comece encontrando\(f′(x)\). Desde
\[f′(x)=\cos x \nonumber \]
e
\[f′\big(g(x)\big)=\cos \big( \sin^{−1}x\big)=\sqrt{1−x^2} \nonumber \]
nós vemos isso
\[g′(x)=\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{f′\big(g(x)\big)}=\dfrac{1}{\sqrt{1−x^2}} \nonumber \]
Análise
Para ver isso\(\cos(\sin^{−1}x)=\sqrt{1−x^2}\), considere o seguinte argumento. Conjunto\(\sin^{−1}x=θ\). Nesse caso,\(\sin θ=x\) onde\(−\frac{π}{2}≤θ≤\frac{π}{2}\). Começamos considerando o caso em que\(0<θ<\frac{π}{2}\). Como\(θ\) é um ângulo agudo, podemos construir um triângulo reto com ângulo agudo\(θ\), uma hipotenusa de comprimento\(1\) e o lado oposto\(θ\) com comprimento\(x\). Do teorema de Pitágoras, o lado adjacente ao ângulo\(θ\) tem comprimento\(\sqrt{1−x^2}\). Esse triângulo é mostrado na Figura\(\PageIndex{2}\) Usando o triângulo, vemos isso\(\cos(\sin^{−1}x)=\cos θ=\sqrt{1−x^2}\).
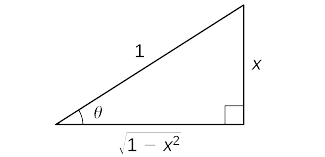
No caso em que\(−\frac{π}{2}<θ<0\), fazemos a observação de que\(0<−θ<\frac{π}{2}\) e, portanto,
\(\cos\big(\sin^{−1}x\big)=\cos θ=\cos(−θ)=\sqrt{1−x^2}\).
Agora, se\(θ=\frac{π}{2}\)\(θ=−\frac{π}{2},x=1\) ou ou\(x=−1\), e já que em qualquer caso\(\cosθ=0\) e\(\sqrt{1−x^2}=0\), temos
\(\cos\big(\sin^{−1}x\big)=\cosθ=\sqrt{1−x^2}\).
Consequentemente, em todos os casos,
\[\cos\big(\sin^{−1}x\big)=\sqrt{1−x^2}.\nonumber \]
Aplique a regra da cadeia à fórmula derivada em Exemplo\(\PageIndex{4A}\) para encontrar a derivada de\(h(x)=\sin^{−1}\big(g(x)\big)\) e use esse resultado para encontrar a derivada de\(h(x)=\sin^{−1}(2x^3).\)
Solução
Aplicando a regra da cadeia a\(h(x)=\sin^{−1}\big(g(x)\big)\), temos
\(h′(x)=\dfrac{1}{\sqrt{1−\big(g(x)\big)^2}}g′(x)\).
Agora deixe que\(g(x)=2x^3,\) assim seja\(g′(x)=6x^2\). Substituindo o resultado anterior, obtemos
\(\begin{align*} h′(x)&=\dfrac{1}{\sqrt{1−4x^6}}⋅6x^2\\[4pt]&=\dfrac{6x^2}{\sqrt{1−4x^6}}\end{align*}\)
Use o teorema da função inversa para encontrar a derivada de\(g(x)=\tan^{−1}x\).
- Dica
-
O inverso de\(g(x)\) é\(f(x)=\tan x\). Use o exemplo\(\PageIndex{4A}\) como guia.
- Responda
-
\(g′(x)=\dfrac{1}{1+x^2}\)
As derivadas das demais funções trigonométricas inversas também podem ser encontradas usando o teorema da função inversa. Essas fórmulas são fornecidas no seguinte teorema.
\[\begin{align} \dfrac{d}{dx}\big(\sin^{−1}x\big) &=\dfrac{1}{\sqrt{1−x^2}} \label{trig1} \\[4pt] \dfrac{d}{dx}\big(\cos^{−1}x\big) &=\dfrac{−1}{\sqrt{1−x^2}} \label{trig2} \\[4pt] \dfrac{d}{dx}\big(\tan^{−1}x\big) &=\dfrac{1}{1+x^2} \label{trig3} \\[4pt] \dfrac{d}{dx}\big(\cot^{−1}x\big) &=\dfrac{−1}{1+x^2} \label{trig4} \\[4pt] \dfrac{d}{dx}\big(\sec^{−1}x\big) &=\dfrac{1}{|x|\sqrt{x^2−1}} \label{trig5} \\[4pt] \dfrac{d}{dx}\big(\csc^{−1}x\big) &=\dfrac{−1}{|x|\sqrt{x^2−1}} \label{trig6} \end{align} \]
Encontre a derivada de\(f(x)=\tan^{−1}(x^2).\)
Solução
Deixe\(g(x)=x^2\), então\(g′(x)=2x\). Substituindo na Equação\ ref {trig3}, obtemos
\(f′(x)=\dfrac{1}{1+(x^2)^2}⋅(2x).\)
Simplificando, temos
\(f′(x)=\dfrac{2x}{1+x^4}\).
Encontre a derivada de\(h(x)=x^2 \sin^{−1}x.\)
Solução
Ao aplicar a regra do produto, temos
\(h′(x)=2x\sin^{−1}x+\dfrac{1}{\sqrt{1−x^2}}⋅x^2\)
Encontre a derivada de\(h(x)=\cos^{−1}(3x−1).\)
- Dica
-
Use Equation\ ref {trig2}. com\(g(x)=3x−1\)
- Responda
-
\(h′(x)=\dfrac{−3}{\sqrt{6x−9x^2}}\)
A posição de uma partícula no momento\(t\) é dada por\(s(t)=\tan^{−1}\left(\frac{1}{t}\right)\) for\(t≥ \ce{1/2}\). Encontre a velocidade da partícula no momento\( t=1\).
Solução
Comece diferenciando\(s(t)\) para encontrar\(v(t)\). Assim,
\(v(t)=s′(t)=\dfrac{1}{1+\left(\frac{1}{t}\right)^2}⋅\dfrac{−1}{t^2}\).
Simplificando, temos
\(v(t)=−\dfrac{1}{t^2+1}\).
Assim,\(v(1)=−\dfrac{1}{2}.\)
Encontre a equação da reta tangente ao gráfico de\(f(x)=\sin^{−1}x\) em\(x=0.\)
- Dica
-
\(f′(0)\)é a inclinação da reta tangente.
- Responda
-
\(y=x\)
Conceitos-chave
- O teorema da função inversa nos permite calcular derivadas de funções inversas sem usar a definição de limite da derivada.
- Podemos usar o teorema da função inversa para desenvolver fórmulas de diferenciação para as funções trigonométricas inversas.
Equações-chave
- Teorema da função inversa
\((f^{−1})′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}\)sempre\(f′\big(f^{−1}(x)\big)≠0\) e\(f(x)\) é diferenciável.
- Regra de potência com expoentes racionais
\(\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}.\)
- Derivada da função senoidal inversa
\(\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{\sqrt{1−x^2}}\)
- Derivada da função inversa do cosseno
\(\dfrac{d}{dx}\big(\cos^{−1}x\big)=\dfrac{−1}{\sqrt{1−x^2}}\)
Derivada da função tangente inversa
\(\dfrac{d}{dx}\big(\tan^{−1}x\big)=\dfrac{1}{1+x^2}\)
Derivada da função cotangente inversa
\(\dfrac{d}{dx}\big(\cot^{−1}x\big)=\dfrac{−1}{1+x^2}\)
Derivada da função secante inversa
\(\dfrac{d}{dx}\big(\sec^{−1}x\big)=\dfrac{1}{|x|\sqrt{x^2−1}}\)
Derivada da função cossecante inversa
\(\dfrac{d}{dx}\big(\csc^{−1}x\big)=\dfrac{−1}{|x|\sqrt{x^2−1}}\)
Contribuidores e atribuições
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) added the second half of Example \(\PageIndex{2}\).


