3.8E: Exercícios para a Seção 3.8

Last updated
Save as PDF

Page ID: 188480

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 10, use a diferenciação implícita para encontrar$\dfrac{dy}{dx}$.

1)$x^2−y^2=4$

2)$6x^2+3y^2=12$

Responda: $\dfrac{dy}{dx}=\dfrac{−2x}{y}$

3)$x^2y=y−7$

4)$3x^3+9xy^2=5x^3$

Responda: $\dfrac{dy}{dx}=\dfrac{x}{3y}−\dfrac{y}{2x}$

5)$xy−\cos(xy)=1$

6)$y\sqrt{x+4}=xy+8$

Responda: $\dfrac{dy}{dx}=\dfrac{y−\dfrac{y}{2\sqrt{x+4}}}{\sqrt{x+4}−x}$

7)$−xy−2=\frac{x}{7}$

8)$y\sin(xy)=y^2+2$

Responda: $\dfrac{dy}{dx}=\dfrac{y^2\cos(xy)}{2y−\sin(xy)−xy\cos(xy)}$

9)$(xy)^2+3x=y^2$

10)$x^3y+xy^3=−8$

Responda: $\dfrac{dy}{dx}=\dfrac{−3x^2y−y^3}{x^3+3xy^2}$

Para os exercícios 11 a 16, encontre a equação da reta tangente ao gráfico da equação dada no ponto indicado. Use uma calculadora ou um software de computador para representar graficamente a função e a reta tangente.

11) [T]$x^4y−xy^3=−2, \quad (−1,−1)$

12) [T]$x^2y^2+5xy=14,\quad (2,1)$

Responda

$y=−\frac{1}{2}x+2$

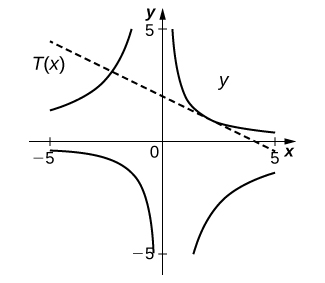
$O gráfico tem um crescente em cada um dos quatro quadrantes. Há uma linha reta marcada com T (x) com inclinação −1/2 e intercepto y 2.$

13) [T]$\tan(xy)=y,\quad \left(\frac{π}{4},1\right)$

14) [T]$xy^2+\sin(πy)−2x^2=10, \quad (2,−3)$

Responda

$y=\frac{1}{π+12}x−\frac{3π+38}{π+12}$

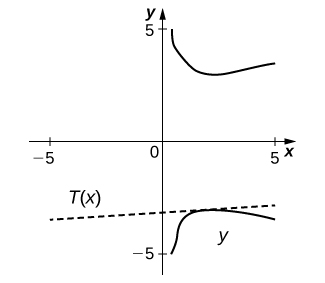
$O gráfico tem duas curvas, uma no primeiro quadrante e outra no quarto quadrante. Eles são simétricos em relação ao eixo x. A curva no primeiro quadrante vai de (0,3, 5) a (1,5, 3,5) a (5, 4). Há uma linha reta marcada com T (x) com inclinação 1/ (π + 12) e intercepto y − (3π + 38)/(π + 12).$

15) [T]$\dfrac{x}{y}+5x−7=−\frac{3}{4}y, \quad (1,2)$

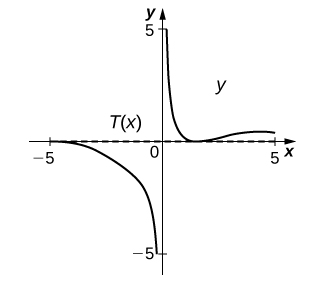
16) [T]$xy+\sin(x)=1,\quad \left(\frac{π}{2},0\right)$

Responda

$y=0$

$O gráfico começa no terceiro quadrante próximo a (−5, 0), permanece próximo de 0 até x = −4, ponto em que diminui até chegar perto de (0, −5). Há uma assíntota em x = 0. O gráfico começa novamente perto de (0, 5) diminuir para (1, 0) e depois aumenta um pouco antes de diminuir para ficar próximo (5, 0). Há uma linha reta marcada com T (x) que coincide com y = 0.$

17) [T] O gráfico de um fólio de Descartes com equação$2x^3+2y^3−9xy=0$ é dado no gráfico a seguir.

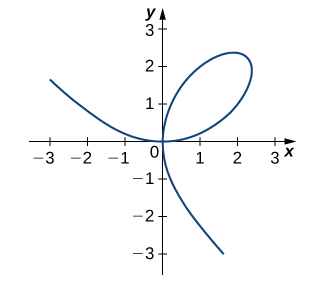
$Um fólio é representado graficamente com a equação 2x3 + 2y3 — 9xy = 0. Ele cruza sobre si mesmo em (0, 0).$

a. Encontre a equação da reta tangente no ponto$(2,1)$. Faça um gráfico da linha tangente junto com o fólio.

b. Encontre a equação da reta normal com a reta tangente em a. no ponto$(2,1)$.

18) Para a equação$x^2+2xy−3y^2=0,$

a. Encontre a equação da normal em relação à reta tangente no ponto$(1,1)$.

b. Em que outro ponto a linha normal em a. cruza o gráfico da equação?

Responda: a.$y=−x+2$
b.$(3,−1)$

19) Encontre todos os pontos no gráfico$y^3−27y=x^2−90$ em que a reta tangente é vertical.

20) Para a equação$x^2+xy+y^2=7$,

a. Encontre o (s)$x$ intercepto (s) -.

b. Encontre a inclinação da (s) reta (s) tangente (s) no (s)$x$ intercepto (s).

c. O que o (s) valor (es) na parte b. indicam sobre a (s) reta (s) tangente (s)?

Responda: a.$\left(±\sqrt{7},0\right)$
b.$−2$
c. Eles são paralelos, pois a inclinação é a mesma em ambas as interceptações.

21) Encontre a equação da reta tangente ao gráfico da equação$\sin^{−1}x+\sin^{−1}y=\frac{π}{6}$ no ponto$\left(0,\frac{1}{2}\right)$.

22) Encontre a equação da reta tangente ao gráfico da equação$\tan^{−1}(x+y)=x^2+\frac{π}{4}$ no ponto$(0,1)$.

Responda: $y=−x+1$

23) Encontre$y′$ e$y''$ para$x^2+6xy−2y^2=3$.

24) [T] O número de telefones celulares produzidos quando$x$ dólares são gastos em mão de obra e$y$ dólares são gastos em capital investido por um fabricante pode ser modelado pela equação$60x^{3/4}y^{1/4}=3240$.

a. Encontre$\frac{dy}{dx}$ e avalie no ponto$(81,16)$.

b. Interprete o resultado de a.

Responda: a.$\frac{dy}{dx}=−0.5926$
b. Quando $81 são gastos em mão de obra e $16 são gastos em capital, o valor gasto em capital está diminuindo em $0,5926 por $1 gasto em mão de obra.

25) [T] O número de carros produzidos quando$x$ dólares são gastos em mão de obra e$y$ dólares são gastos em capital investido por um fabricante pode ser modelado pela equação$30x^{1/3}y^{2/3}=360$.

(Ambos$x$$y$ são medidos em milhares de dólares.)

a. Encontre$\frac{dy}{dx}$ e avalie no ponto$(27,8)$.

b. Interprete o resultado da parte a.

26) O volume de um cone circular reto de raio$x$ e altura$y$ é dado por$V=\frac{1}{3}πx^2y$. Suponha que o volume do cone seja$85π\,\text{cm}^3$. Descubra$\dfrac{dy}{dx}$ quando$x=4$$y=16$ e.

Responda: $\dfrac{dy}{dx} = −8$

Para os exercícios 27 a 28, considere uma caixa retangular fechada com uma base quadrada com lado$x$ e altura$y$.

27) Encontre uma equação para a área da superfície da caixa retangular,$S(x,y)$.

28) Se a área da superfície da caixa retangular for 78 pés quadrados, encontre$\dfrac{dy}{dx}$ quando$x=3$ pés e$y=5$ pés.

Responda: $\dfrac{dy}{dx} = −2.67$

Nos exercícios 29 a 31, use a diferenciação implícita para determinar$y′$. A resposta concorda com as fórmulas que determinamos anteriormente?

29)$x=\sin y$

30)$x=\cos y$

Responda: $y′=−\dfrac{1}{\sqrt{1−x^2}}$

31)$x=\tan y$