3.9: Derivadas de funções exponenciais e logarítmicas
- Page ID
- 188397
- Encontre a derivada das funções exponenciais.
- Encontre a derivada das funções logarítmicas.
- Use a diferenciação logarítmica para determinar a derivada de uma função.
Até agora, aprendemos como diferenciar uma variedade de funções, incluindo funções trigonométricas, inversas e implícitas. Nesta seção, exploramos derivadas de funções exponenciais e logarítmicas. Conforme discutimos em Introdução às Funções e Gráficos, as funções exponenciais desempenham um papel importante na modelagem do crescimento populacional e da decomposição de materiais radioativos. As funções logarítmicas podem ajudar a redimensionar grandes quantidades e são particularmente úteis para reescrever expressões complicadas.
Derivada da função exponencial
Assim como quando encontramos as derivadas de outras funções, podemos encontrar as derivadas de funções exponenciais e logarítmicas usando fórmulas. À medida que desenvolvemos essas fórmulas, precisamos fazer certas suposições básicas. As provas que essas suposições sustentam estão além do escopo deste curso.
Em primeiro lugar, começamos com a suposição de que a função\(B(x)=b^x,\, b>0,\) é definida para cada número real e é contínua. Em cursos anteriores, os valores das funções exponenciais para todos os números racionais foram definidos — começando com a definição de\(b^n\), onde\(n\) está um número inteiro positivo — como o produto da\(b\) multiplicação por si só\(n\) vezes. Posteriormente\(b^0=1,b^{−n}=\dfrac{1}{b^n}\), definimos, para um inteiro\(n\) positivo e\(b^{s/t}=(\sqrt[t]{b})^s\) para números inteiros positivos\(s\)\(t\) e. Essas definições deixam em aberto a questão do valor de\(b^r\) onde\(r\) está um número real arbitrário. Ao assumir a continuidade de\(B(x)=b^x,b>0\), podemos interpretar\(b^r\) como\(\displaystyle \lim_{x→r}b^x\) onde os valores de\(x\) conforme consideramos o limite são racionais. Por exemplo, podemos ver\(4^π\) como o número satisfatório
\[4^3<4^π<4^4,\quad 4^{3.1}<4^π<4^{3.2},\quad 4^{3.14}<4^π<4^{3.15}, \nonumber \]
\[4^{3.141}<4^{π}<4^{3.142},\quad 4^{3.1415}<4^{π}<4^{3.1416},\quad …. \nonumber \]
Como vemos na tabela a seguir,\(4^π≈77.88.\)
| \(x\) | \(4^x\) | \(x\) | \(4^x\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">\(4^3\) | \ (4^x\)” style="text-align:center; ">64 | \ (x\)” style="text-align:center; ">\(4^{3.141593}\) | \ (4^x\)” style="alinhamento de texto: centro; ">77.8802710486 |
| \ (x\)” style="text-align:center; ">\(4^{3.1}\) | \ (4^x\)” style="alinhamento do texto: centro; ">73,5166947198 | \ (x\)” style="text-align:center; ">\(4^{3.1416}\) | \ (4^x\)” style="alinhamento de texto: centro; ">77.8810268071 |
| \ (x\)” style="text-align:center; ">\(4^{3.14}\) | \ (4^x\)” style="alinhamento de texto: centro; ">77.7084726013 | \ (x\)” style="text-align:center; ">\(4^{3.142}\) | \ (4^x\)” style="alinhamento de texto: centro; ">77.9242251944 |
| \ (x\)” style="text-align:center; ">\(4^{3.141}\) | \ (4^x\)” style="alinhamento de texto: centro; ">77.8162741237 | \ (x\)” style="text-align:center; ">\(4^{3.15}\) | \ (4^x\)” style="alinhamento de texto: centro; ">78.7932424541 |
| \ (x\)” style="text-align:center; ">\(4^{3.1415}\) | \ (4^x\)” style="alinhamento de texto: centro; ">77.8702309526 | \ (x\)” style="text-align:center; ">\(4^{3.2}\) | \ (4^x\)” style="alinhamento do texto: centro; ">84,4485062895 |
| \ (x\)” style="text-align:center; ">\(4^{3.14159}\) | \ (4^x\)” style="alinhamento do texto: centro; ">77.8799471543 | \ (x\)” style="text-align:center; ">\(4^{4}\) | \ (4^x\)” style="text-align:center; ">256 |
Aproximando um valor de\(4^π\)
Também assumimos que\(B(x)=b^x,\, b>0\), para, o valor\(B′(0)\) da derivada existe. Nesta seção, mostramos que, ao fazer essa suposição adicional, é possível provar que a função\(B(x)\) é diferenciável em todos os lugares.
Fazemos uma suposição final: que existe um valor único de\(b>0\) para o qual\(B′(0)=1\). Definimos e como esse valor único, como fizemos em Introdução às Funções e Gráficos. \(\PageIndex{1}\)A figura fornece gráficos das funções\(y=2^x, \,y=3^x, \,y=2.7^x,\)\(y=2.8^x\) e. Uma estimativa visual das inclinações das retas tangentes a essas funções em 0 fornece evidências de que o valor de e está em algum lugar entre 2,7 e 2,8. A função\(E(x)=e^x\) é chamada de função exponencial natural. Seu inverso\(L(x)=\log_e x=\ln x\) é chamado de função logarítmica natural.
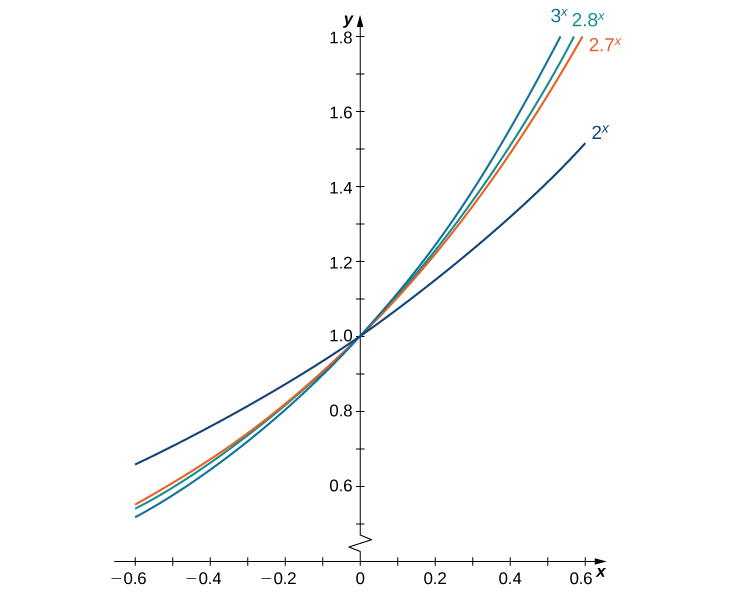
Para uma melhor estimativa de\(e\), podemos construir uma tabela de estimativas de\(B′(0)\) para funções do formulário\(B(x)=b^x\). Antes de fazer isso, lembre-se de que
\[B′(0)=\lim_{x→0}\frac{b^x−b^0}{x−0}=\lim_{x→0}\frac{b^x−1}{x}≈\frac{b^x−1}{x} \nonumber \]
para valores\(x\) muito próximos de zero. Para nossas estimativas, escolhemos\(x=0.00001\) e\(x=−0.00001\)
para obter a estimativa
\[\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}. \nonumber \]
Veja a tabela a seguir.
| \(b\) | \(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\) | \(b\) | \(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\) |
|---|---|---|---|
| \ (b\)” style="text-align:center; ">2 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.693145<B′(0)<0.69315\) | \ (b\)” style="text-align:center; ">2.7183 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000002<B′(0)<1.000012\) |
| \ (b\)” style="text-align:center; ">2.7 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.993247<B′(0)<0.993257\) | \ (b\)” style="text-align:center; ">2.719 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000259<B′(0)<1.000269\) |
| \ (b\)” style="text-align:center; ">2,71 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.996944<B′(0)<0.996954\) | \ (b\)” style="text-align:center; ">2,72 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000627<B′(0)<1.000637\) |
| \ (b\)” style="text-align:center; ">2.718 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.999891<B′(0)<0.999901\) | \ (b\)” style="text-align:center; ">2.8 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.029614<B′(0)<1.029625\) |
| \ (b\)” style="text-align:center; ">2.7182 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.999965<B′(0)<0.999975\) | \ (b\)” style="text-align:center; ">3 | \ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′S (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.098606<B′(0)<1.098618\) |
A evidência da tabela sugere que\(2.7182<e<2.7183.\)
O gráfico de\(E(x)=e^x\) junto com a linha\(y=x+1\) é mostrado na Figura\(\PageIndex{2}\). Essa linha é tangente ao gráfico de\(E(x)=e^x\) at\(x=0\).
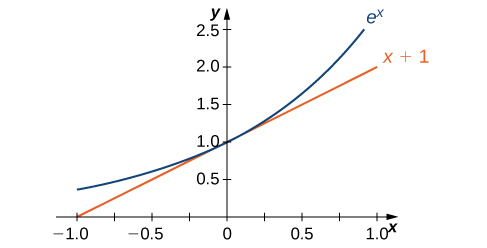
Agora que definimos nossas suposições básicas, começamos nossa investigação explorando a derivada de\(B(x)=b^x, \,b>0\). Lembre-se de que presumimos que isso\(B′(0)\) existe. Ao aplicar a definição de limite à derivada, concluímos que
\[B′(0)=\lim_{h→0}\frac{b^{0+h}−b^0}{h}=\lim_{h→0}\frac{b^h−1}{h} \nonumber \]
Passando para\(B′(x)\), obtemos o seguinte.
\ (\ displaystyle\ begin {align*} B′( x) &=\ lim_ {h→0}\ frac {b^ {x+h} −b^x} {h} &\ text {Aplique a definição limite da derivada.}\\ [4pt]
&=\ lim_ {h→0}\ frac {b^xb^h−b^x} {h} & &\ text {Note que} b^ {x+h} =b^xb^h.\\ [4pt]
&=\ lim_ {h→0}\ frac {b^x (b^h−1)} {h} & &\ text {Factor out} b^x.\\ [4pt]
&=b^x\ lim_ {h→0}\ frac {b^h−1} {h} & &\ text {Aplique uma propriedade de limites.}\\ [4pt]
&=B^xB′( 0) & &\ text {Use} B′B′0 (0) =\ lim_ {h→0}\ frac {b^b` ^ {0+h} −b^0} {h} =\ lim_ {h→0}\ frac {b^h−1} {h}. \ end {align*}\)
Vemos que, com base na suposição de que\(B(x)=b^x\) é diferenciável, não\(0,B(x)\) é apenas diferenciável em todos os lugares, mas sua derivada é
\[B′(x)=b^xB′(0).\nonumber \]
\(E(x)=e^x, \,E′(0)=1.\)Pois assim, nós temos\(E′(x)=e^x\). (O valor de\(B′(0)\) para uma função arbitrária do formulário\(B(x)=b^x, \,b>0,\) será derivado posteriormente.)
\(E(x)=e^x\)Seja a função exponencial natural. Então
\[E′(x)=e^x. \nonumber \]
Em geral,
\[\frac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x) \nonumber \]
Encontre a derivada de\(f(x)=e^{\tan(2x)}\).
Solução:
Usando a fórmula derivada e a regra da cadeia,
\[f′(x)=e^{\tan(2x)}\frac{d}{dx}\Big(\tan(2x)\Big)=e^{\tan(2x)}\sec^2(2x)⋅2 \nonumber \]
Encontre a derivada de\(y=\dfrac{e^{x^2}}{x}\).
Solução
Use a derivada da função exponencial natural, a regra do quociente e a regra da cadeia.
\ (\ begin {align*} y′&=\ dfrac {(e^ {x^2} ⋅2) x⋅x−1⋅e^ {x^2}} {x^2} & &\ text {Aplique a regra do quociente.}\\ [4pt]
&=\ dfrac {e^ {x^2} (2x^2−1)} {x^2} & &\ text {Simplifique.} \ end {align*}\)
Encontre a derivada de\(h(x)=xe^{2x}\).
- Dica
-
Não se esqueça de usar a regra do produto.
- Resposta
-
\(h′(x)=e^{2x}+2xe^{2x}\)
Uma colônia de mosquitos tem uma população inicial de 1000. Depois de\(t\) dias, a população é dada por\(A(t)=1000e^{0.3t}\). Mostre que a proporção da taxa de variação da população,\(A′(t)\), para a população,\(A(t)\) é constante.
Solução
Primeira descoberta\(A′(t)\). Usando a regra da cadeia, temos\(A′(t)=300e^{0.3t}.\) Assim, a razão entre a taxa de mudança da população e a população é dada por
\[\frac{A′(t)}{A(t)}=\frac{300e^{0.3t}}{1000e^{0.3t}}=0.3. \nonumber \]
A razão entre a taxa de variação da população e a população é a constante de 0,3.
Se\(A(t)=1000e^{0.3t}\) descreve a população de mosquitos após\(t\) dias, como no exemplo anterior, qual é a taxa de variação\(A(t)\) após 4 dias?
- Dica
-
Encontre\(A′(4)\).
- Resposta
-
\(996\)
Derivada da função logarítmica
Agora que temos a derivada da função exponencial natural, podemos usar a diferenciação implícita para encontrar a derivada de sua inversa, a função logarítmica natural.
Se\(x>0\) e\(y=\ln x\), então
\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]
De forma mais geral,\(g(x)\) seja uma função diferenciável. Para todos os valores dos\(x\) quais\(g′(x)>0\), a derivada de\(h(x)=\ln(g(x))\) é dada por
\[h′(x)=\frac{1}{g(x)}g′(x). \nonumber \]
Se\(x>0\) e\(y=\ln x\), então,\(e^y=x.\) diferenciar os dois lados dessa equação resulta na equação
\[e^y\frac{dy}{dx}=1. \nonumber \]
Solução para obter\(\dfrac{dy}{dx}\) rendimentos
\[\frac{dy}{dx}=\frac{1}{e^y}. \nonumber \]
Finalmente, substituímos\(x=e^y\) para obter
\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]
Também podemos derivar esse resultado aplicando o teorema da função inversa, da seguinte forma. Desde\(y=g(x)=\ln x\)
é o inverso de\(f(x)=e^x\), aplicando o teorema da função inversa que temos
\[\frac{dy}{dx}=\frac{1}{f′(g(x))}=\frac{1}{e^{\ln x}}=\frac{1}{x}. \nonumber \]
Usando esse resultado e aplicando a regra da cadeia aos\(h(x)=\ln(g(x))\) rendimentos
\[h′(x)=\frac{1}{g(x)}g′(x). \label{lnder} \]
□
O gráfico de\(y=\ln x\) e sua derivada\(\dfrac{dy}{dx}=\dfrac{1}{x}\) são mostrados na Figura\(\PageIndex{3}\).
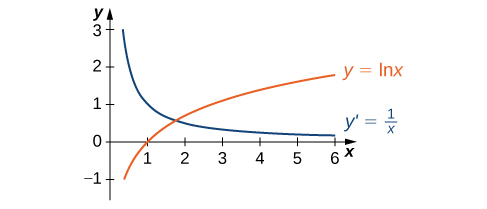
Encontre a derivada de\(f(x)=\ln(x^3+3x−4)\).
Solução
Use Equation\ ref {lnder} diretamente.
\ (\ begin {align*} f′( x) &=\ dfrac {1} {x^3+3x−4} ‣ (3x^2+3) & &\ text {Use} g (x) =x^3+3x−4\ texto {in} h′( x) =\ dfrac {1} {g (x)} g′n (x).\\ [4" pt]
&=\ dfrac {3x^2+3} {x^3+3x−4} & &\ text {Reescrever.} \ end {align*}\)
Encontre a derivada de\(f(x)=\ln\left(\dfrac{x^2\sin x}{2x+1}\right)\).
Solução
À primeira vista, tomar essa derivada parece bastante complicado. No entanto, usando as propriedades dos logaritmos antes de encontrar a derivada, podemos tornar o problema muito mais simples.
\ (\ begin {align*} f (x) &=\ ln\ left (\ frac {x^2\ sin x} {2x+1}\ right) =2\ ln x+\ ln (\ sin x) −\ ln (2x+1) & &\ text {Aplicar propriedades dos logaritmos.}\\ [4pt]
f′( x) &=\ dfrac {2} {x} +\ cot x−\ dfrac {2} {2x+1} & &\ text {Aplique a regra da soma e} h′( x) =\ dfrac {1} {g (x)} g′d (x). \ end {align*}\)
Diferenciar:\(f(x)=\ln(3x+2)^5\).
- Dica
-
Use uma propriedade dos logaritmos para simplificar antes de tomar a derivada.
- Resposta
-
\(f′(x)=\dfrac{15}{3x+2}\)
Agora que podemos diferenciar a função logarítmica natural, podemos usar esse resultado para encontrar as derivadas de\(y=\log_b x\) e\(y=b^x\) para\(b>0, \,b≠1\).
Seja\(b>0,b≠1,\) e deixe\(g(x)\) ser uma função diferenciável.
i. Se\(y=\log_b x\), então
\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]
De forma mais geral, se\(h(x)=\log_b(g(x))\), então, para todos os valores de\(x\) para os quais\(g(x)>0\),
\[h′(x)=\frac{g′(x)}{g(x)\ln b}. \label{genlogder} \]
ii. Se\(y=b^x,\) então
\[\frac{dy}{dx}=b^x\ln b. \nonumber \]
De forma mais geral, se\(h(x)=b^{g(x)},\) então
\[h′(x)=b^{g(x)}g'(x)\ln b \label{genexpder} \]
Se\(y=\log_b x,\) então\(b^y=x.\), segue isso\(\ln(b^y)=\ln x\). Assim\(y\ln b=\ln x\). Resolvendo para\(y\), nós temos\(y=\dfrac{\ln x}{\ln b}\). Diferenciando e tendo em mente que isso\(\ln b\) é uma constante, vemos que
\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]
A derivada na Equação\ ref {genlogder} agora segue da regra da cadeia.
Se\(y=b^x\). Em seguida,\(\ln y=x\ln b.\) usando diferenciação implícita, novamente tendo em mente que\(\ln b\) é constante, segue isso\(\dfrac{1}{y}\dfrac{dy}{dx}=\ln b\). Resolvendo\(\dfrac{dy}{dx}\) e substituindo\(y=b^x\), vemos que
\[\frac{dy}{dx}=y\ln b=b^x\ln b. \nonumber \]
A derivada mais geral (Equation\ ref {genexpder}) segue da regra da cadeia.
□
Encontre a derivada de\(h(x)=\dfrac{3^x}{3^x+2}\).
Solução
Use a regra do quociente e o Note.
\ (\ begin {align*} h′( x) &=\ dfrac {3^x\ ln 3 (3^x+2) −3^x\ ln 3 (3^x)} {(3^x+2) ^2} & &\ text {Aplique a regra do quociente.}\\ [4pt]
&=\ dfrac {2⋅3^x\ ln 3} {(3pt] x+2) ^2} & &\ text {Simplifique.} \ end {align*}\)
Encontre a inclinação da reta tangente ao gráfico de\(y=\log_2 (3x+1)\) at\(x=1\).
Solução
Para encontrar a inclinação, devemos avaliar\(\dfrac{dy}{dx}\) em\(x=1\). Usando a Equação\ ref {genlogder}, vemos que
\[\frac{dy}{dx}=\frac{3}{(3x+1)\ln 2}. \nonumber \]
Ao avaliar a derivada em\(x=1\), vemos que a reta tangente tem inclinação
\[\frac{dy}{dx}\bigg{|}_{x=1}=\frac{3}{4\ln 2}=\frac{3}{\ln 16}. \nonumber \]
Encontre a inclinação da reta tangente a\(y=3^x\) at\(x=2.\)
- Dica
-
Avalie a derivada em\(x=2.\)
- Resposta
-
\(9\ln(3)\)
Diferenciação logarítmica
Neste ponto, podemos obter derivadas de funções da forma\(y=(g(x))^n\) para certos valores de\(n\), bem como funções da forma\(y=b^{g(x)}\), onde\(b>0\)\(b≠1\) e. Infelizmente, ainda não conhecemos as derivadas de funções como\(y=x^x\) ou\(y=x^π\). Essas funções requerem uma técnica chamada diferenciação logarítmica, que nos permite diferenciar qualquer função da forma\(h(x)=g(x)^{f(x)}\). Também pode ser usado para converter um problema de diferenciação muito complexo em um mais simples, como encontrar a derivada de\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\). Descrevemos essa técnica na seguinte estratégia de resolução de problemas.
- Para diferenciar\(y=h(x)\) usando a diferenciação logarítmica, use o logaritmo natural de ambos os lados da equação para obter\(\ln y=\ln(h(x)).\)
- Use as propriedades dos logaritmos para expandir o\(\ln(h(x))\) máximo possível.
- Diferencie os dois lados da equação. À esquerda, teremos\(\dfrac{1}{y}\dfrac{dy}{dx}\).
- Multiplique os dois lados da equação por\(y\) para resolver\(\dfrac{dy}{dx}\).
- Substituir\(y\) por\(h(x)\).
Encontre a derivada de\(y=(2x^4+1)^{\tan x}\).
Solução
Use a diferenciação logarítmica para encontrar essa derivada.
\ (\ begin {align*}\ ln y&=\ ln (2x^4+1) ^ {\ tan x} & &\ text {Etapa 1. Pegue o logaritmo natural de ambos os lados.}\\ [4pt]
\ ln y&=\ tan x\ ln (2x^4+1) & &\ text {Etapa 2. Expanda usando as propriedades dos logaritmos.}\
\ [4pt]\ dfrac {1} {y}\ dfrac {dy} {dx} &=\ sec^2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ↑\ tan x & &\ text {Etapa 3. Diferencie os dois lados. Use a regra do produto à direita.}\\ [4pt]
\ dfrac {dy} {dx} &=yρ (\ sec^2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ≠\ tan x) & &\ text {Etapa 4. Multiplique por} y\ text {em ambos os lados.}\\ [4pt]
\ dfrac {dy} {dx} & =( 2x^4+1) ^ {\ tan x} (\ sec^2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ‣\ tan x) &\ text {Etapa 5. Substitua} y= (2x^4+1) ^ {\ tan x}. \ end {align*}\)
Encontre a derivada de\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\).
Solução
Esse problema realmente faz uso das propriedades dos logaritmos e das regras de diferenciação dadas neste capítulo.
| \(\ln y=\ln\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\) | Etapa 1. Pegue o logaritmo natural dos dois lados. |
| \(\ln y=\ln x+\frac{1}{2}\ln(2x+1)−x\ln e−3\ln \sin x\) | Etapa 2. Expanda usando as propriedades dos logaritmos. |
| \(\dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\dfrac{\cos x}{\sin x}\) | Etapa 3. Diferencie os dois lados. |
| \(\dfrac{dy}{dx}=y\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\) | Etapa 4. Multiplique por\(y\) em ambos os lados. |
| \(\dfrac{dy}{dx}=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\) | Etapa 5. Substituto\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}.\) |
Use a diferenciação logarítmica para encontrar a derivada de\(y=x^x\).
- Dica
-
Siga a estratégia de resolução de problemas.
- Resposta
-
Solução:\(\dfrac{dy}{dx}=x^x(1+\ln x)\)
Encontre a derivada de\(y=(\tan x)^π\).
- Dica
-
Use a regra da potência (já que o expoente\(\pi\) é uma constante) e a regra da cadeia.
- Resposta
-
\(y′=π(\tan x)^{π−1}\sec^2 x\)
Conceitos-chave
- Com base na suposição de que a função exponencial\(y=b^x, \,b>0\) é contínua em todos os lugares e diferenciável em\(0\), essa função é diferenciável em todos os lugares e existe uma fórmula para sua derivada.
- Podemos usar uma fórmula para encontrar a derivada de\(y=\ln x\), e a relação nos\(\log_b x=\dfrac{\ln x}{\ln b}\) permite estender nossas fórmulas de diferenciação para incluir logaritmos com bases arbitrárias.
- A diferenciação logarítmica nos permite diferenciar funções da forma\(y=g(x)^{f(x)}\) ou funções muito complexas, pegando o logaritmo natural de ambos os lados e explorando as propriedades dos logaritmos antes da diferenciação.
Equações-chave
- Derivada da função exponencial natural
\(\dfrac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x)\)
- Derivada da função logarítmica natural
\(\dfrac{d}{dx}\Big(\ln g(x)\Big)=\dfrac{1}{g(x)}g′(x)\)
- Derivada da função exponencial geral
\(\dfrac{d}{dx}\Big(b^{g(x)}\Big)=b^{g(x)}g′(x)\ln b\)
- Derivada da função logarítmica geral
\(\dfrac{d}{dx}\Big(\log_b g(x)\Big)=\dfrac{g′(x)}{g(x)\ln b}\)
Glossário
- diferenciação logarítmica
- é uma técnica que nos permite diferenciar uma função tomando primeiro o logaritmo natural de ambos os lados de uma equação, aplicando propriedades de logaritmos para simplificar a equação e diferenciando implicitamente


