3.5: Derivadas de funções trigonométricas
- Page ID
- 188427
- Encontre as derivadas da função seno e cosseno.
- Encontre as derivadas das funções trigonométricas padrão.
- Calcule as derivadas de ordem superior do seno e do cosseno.
Um dos tipos mais importantes de movimento na física é o movimento harmônico simples, associado a sistemas como um objeto com massa oscilando em uma mola. O movimento harmônico simples pode ser descrito usando as funções seno ou cosseno. Nesta seção, expandimos nosso conhecimento de fórmulas derivadas para incluir derivadas dessas e de outras funções trigonométricas. Começamos com as derivadas das funções seno e cosseno e depois as usamos para obter fórmulas para as derivadas das quatro funções trigonométricas restantes. Ser capaz de calcular as derivadas das funções seno e cosseno nos permitirá encontrar a velocidade e a aceleração do movimento harmônico simples.
Derivadas das funções seno e cosseno
Começamos nossa exploração da derivada da função seno usando a fórmula para fazer uma estimativa razoável de sua derivada. Lembre-se de que, para uma função\(f(x),\)
\[f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Consequentemente, para valores\(h\) muito próximos de\(0\),
\[f′(x)≈\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Vemos isso usando\(h=0.01\),
\[\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
Ao definir
\[D(x)=\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
e usando um utilitário gráfico, podemos obter um gráfico de uma aproximação à derivada de\(\sin x\) (Figura\(\PageIndex{1}\)).
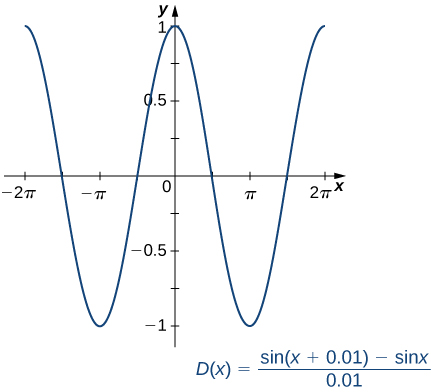
Após a inspeção, o gráfico de\(D(x)\) parece estar muito próximo do gráfico da função cosseno. De fato, mostraremos que
\[\dfrac{d}{dx}(\sin x)=\cos x. \nonumber \]
Se seguíssemos os mesmos passos para aproximar a derivada da função cosseno, descobriríamos que
\[\dfrac{d}{dx}(\cos x)=−\sin x. \nonumber \]
A derivada da função seno é o cosseno e a derivada da função cosseno é o seno negativo.
\[\dfrac{d}{dx}(\sin x)=\cos x \nonumber \]
\[\dfrac{d}{dx}(\cos x)=−\sin x \nonumber \]
Como as provas\(\dfrac{d}{dx}(\sin x)=\cos x\) e o\(\dfrac{d}{dx}(\cos x)=−\sin x\) uso de técnicas semelhantes, fornecemos apenas a prova de\(\dfrac{d}{dx}(\sin x)=\cos x\). Antes de começar, lembre-se de dois limites trigonométricos importantes:
\(\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1\)\(\displaystyle \lim_{h→0}\dfrac{\cos h−1}{h}=0\)e.
Os gráficos de\(y=\dfrac{\sin h}{h}\) e\(y=\dfrac{\cos h−1}{h}\) são mostrados na Figura\(\PageIndex{2}\).
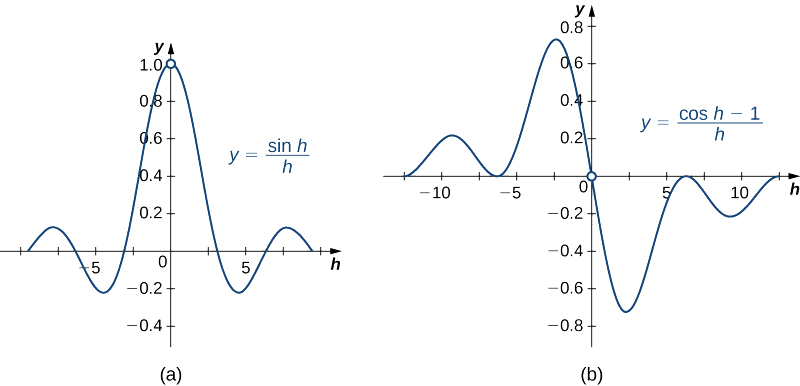
Também lembramos a seguinte identidade trigonométrica para o seno da soma de dois ângulos:
\[\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber \]
Agora que reunimos todas as equações e identidades necessárias, prosseguimos com a prova.
\ [\ begin {align*}\ dfrac {d} {dx} (\ sin x) &=\ lim_ {h→0}\ dfrac {\ sin (x+h) −\ sin x} {h} &\ text {Aplique a definição da derivada.}\\ [4pt]
&=\ lim_ {h→0}\ dfrac {\ sin x\ cos h→ +\ cos x\ sin h−\ sin x} {h} &\ text {Use a identidade trigonométrica para o seno da soma de dois ângulos.}\\ [4pt]
&=\ lim_ {h→0}\ left (\ dfrac {\ sin x\ cos h−\ sin x} {h} +\ dfrac {\ cos x\ sin h} {h}\ direita) &\ text {Reagrupar.}\\ [4pt]
&=\ lim_ {h→0}\ left (\ sin x\ left (\ dfrac {\ cos h−−0} 1} {h}\ right) + (\ cos x)\ left (\ dfrac {\ sin h} {h}\ right)\ right) & &\ text {Fator out}\ sin x\ text {e}\ cos x\\ [4pt]
& =(\ sin x)\ lim_ {h→0}\ left (\ dfrac {\ cos h−1} {h}\ right) + (\ cos x)\ lim_ {h→0}\ left (\ dfrac {\ sin h} {h}\ right) & &\ text {Factor}\ sin x\ text {e}\ cos x\ text {fora dos limites.}\\ [4pt]
& =(\ sin x) (0) + (\ cos x) (1) & &\ text {Aplique fórmulas de limite trigonométrico.}\\ [4pt]
&=\ cos x & &\ text {Simplifique.} \ end {align*}\ nonumber\]
□
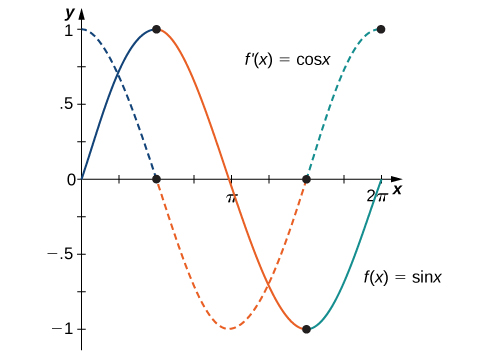
A figura\(\PageIndex{3}\) mostra a relação entre o gráfico de\(f(x)=\sin x\) e sua derivada\(f′(x)=\cos x\). Observe que nos pontos em que\(f(x)=\sin x\) tem uma tangente horizontal, sua derivada\(f′(x)=\cos x\) assume o valor zero. Também vemos que onde f\((x)=\sin x\) está aumentando\(f′(x)=\cos x>0\) e onde\(f(x)=\sin x\) está diminuindo,\(f′(x)=\cos x<0.\)
Encontre a derivada de\(f(x)=5x^3\sin x\).
Solução
Usando a regra do produto, temos
\[ \begin{align*} f'(x) &=\dfrac{d}{dx}(5x^3)⋅\sin x+\dfrac{d}{dx}(\sin x)⋅5x^3 \\[4pt] &=15x^2⋅\sin x+\cos x⋅5x^3. \end{align*}\]
Depois de simplificar, obtemos
\[f′(x)=15x^2\sin x+5x^3\cos x. \nonumber \]
Encontre a derivada de\(f(x)=\sin x\cos x.\)
- Dica
-
Não se esqueça de usar a regra do produto.
- Responda
-
\[f′(x)=\cos^2x−\sin^2x \nonumber \]
Encontre a derivada de\(g(x)=\dfrac{\cos x}{4x^2}\).
Solução
Ao aplicar a regra do quociente, temos
\[g′(x)=\dfrac{(−\sin x)4x^2−8x(\cos x)}{(4x^2)^2}. \nonumber \]
Simplificando, obtemos
\[g′(x)=\dfrac{−4x^2\sin x−8x\cos x}{16x^4}=\dfrac{−x\sin x−2\cos x}{4x^3}. \nonumber \]
Encontre a derivada de\(f(x)=\dfrac{x}{\cos x}\).
- Dica
-
Use a regra do quociente.
- Responda
-
\(f'(x) = \dfrac{\cos x+x\sin x}{\cos^2x}\)
Uma partícula se move ao longo de um eixo coordenado de tal forma que sua posição no tempo\(t\) é dada\(s(t)=2\sin t−t\) por for\(0≤t≤2π.\) Em que momentos a partícula está em repouso?
Solução
Para determinar quando a partícula está em repouso,\(s′(t)=v(t)=0.\) defina Comece encontrando\(s′(t).\) Obtemos
\[s′(t)=2 \cos t−1, \nonumber \]
então devemos resolver
\[2 \cos t−1=0\text{ for }0≤t≤2π. \nonumber \]
As soluções para essa equação são\(t=\dfrac{π}{3}\)\(t=\dfrac{5π}{3}\) e. Assim, a partícula está em repouso às vezes\(t=\dfrac{π}{3}\)\(t=\dfrac{5π}{3}\) e.
Uma partícula se move ao longo de um eixo coordenado. Sua posição no momento\(t\) é dada\(s(t)=\sqrt{3}t+2\cos t\) por for\(0≤t≤2π.\) Em que momentos a partícula está em repouso?
- Dica
-
Use o exemplo anterior como guia.
- Responda
-
\(t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}\)
Derivadas de outras funções trigonométricas
Como as quatro funções trigonométricas restantes podem ser expressas como quocientes envolvendo seno, cosseno ou ambos, podemos usar a regra do quociente para encontrar fórmulas para suas derivadas.
Encontre a derivada de\(f(x)=\tan x.\)
Solução
Comece expressando\(\tan x \) como o quociente de\(\sin x\) e\(\cos x\):
\(f(x)=\tan x =\dfrac{\sin x}{\cos x}\).
Agora aplique a regra do quociente para obter
\(f′(x)=\dfrac{\cos x\cos x−(−\sin x)\sin x}{(\cos x)^2}\).
Simplificando, obtemos
\[f′(x)=\dfrac{\cos^2x+\sin^2 x}{\cos^2x}. \nonumber \]
Reconhecendo que,\(\cos^2x+\sin^2x=1,\) pelo teorema de Pitágoras, agora temos
\[f′(x)=\dfrac{1}{\cos^2x} \nonumber \]
Finalmente, use a identidade\(\sec x=\dfrac{1}{\cos x}\) para obter
\(f′(x)=\text{sec}^2 x\).
Encontre a derivada de\(f(x)=\cot x .\)
- Dica
-
Reescreva\(\cot x \) como\(\dfrac{\cos x}{\sin x}\) e use a regra do quociente.
- Responda
-
\(f′(x)=−\csc^2 x\)
As derivadas das funções trigonométricas restantes podem ser obtidas usando técnicas similares. Nós fornecemos essas fórmulas no seguinte teorema.
As derivadas das funções trigonométricas restantes são as seguintes:
\ [\ begin {align}\ dfrac {d} {dx} (\ tan x) &=\ sec^2x\\ [4pt]
\ dfrac {d} {dx} (\ cot x) &=−\ csc^2x\\ [4pt]
\ dfrac {d} {dx} (\ sec x) &=\ sec x\ tan x\ [4pt]
\ dfrac {d} {dx} (\ csc x) &=−\ csc x\ cot x.\ end {align}\ nonumber\]
Encontre a equação de uma reta tangente ao gráfico de\(f(x)=\cot x \) at\(x=\frac{π}{4}\).
Solução
Para encontrar a equação da reta tangente, precisamos de um ponto e uma inclinação nesse ponto. Para encontrar o ponto, calcule
\(f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1\).
Assim, a reta tangente passa pelo ponto\(\left(\frac{π}{4},1\right)\). Em seguida, encontre a inclinação encontrando a derivada de\(f(x)=\cot x \) e avaliando-a em\(\frac{π}{4}\):
\(f′(x)=−\csc^2 x\)\(f′\left(\frac{π}{4}\right)=−\csc^2\left(\frac{π}{4}\right)=−2\)e.
Usando a equação ponto-inclinação da reta, obtemos
\(y−1=−2\left(x−\frac{π}{4}\right)\)
ou equivalentemente,
\(y=−2x+1+\frac{π}{2}\).
Encontre a derivada de\(f(x)=\csc x+x\tan x .\)
Solução
Para encontrar essa derivada, devemos usar a regra da soma e a regra do produto. Usando a regra da soma, encontramos
\(f′(x)=\dfrac{d}{dx}(\csc x)+\dfrac{d}{dx}(x\tan x )\).
No primeiro termo,\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x ,\) e aplicando a regra do produto ao segundo termo, obtemos
\(\dfrac{d}{dx}(x\tan x )=(1)(\tan x )+(\sec^2 x)(x)\).
Portanto, temos
\(f′(x)=−\csc x\cot x +\tan x +x\sec^2 x\).
Encontre a derivada de\(f(x)=2\tan x −3\cot x .\)
- Dica
-
Use a regra para diferenciar um múltiplo constante e a regra para diferenciar uma diferença de duas funções.
- Responda
-
\(f′(x)=2\sec^2 x+3\csc^2 x\)
Encontre a inclinação da reta tangente ao gráfico de\(f(x)=\tan x \) at\(x=\dfrac{π}{6}\).
- Dica
-
Avalie a derivada em\(x=\dfrac{π}{6}\).
- Responda
-
\(\dfrac{4}{3}\)
Derivados de ordem superior
As derivadas de ordem superior de\(\sin x\) e\(\cos x\) seguem um padrão repetitivo. Seguindo o padrão, podemos encontrar qualquer derivada de ordem superior de\(\sin x\) e\(\cos x.\)
Encontre as quatro primeiras derivadas de\(y=\sin x.\)
Solução
Cada etapa da cadeia é simples:
\ [\ begin {align*} y&=\ sin x\\ [4pt]
\ dfrac {dy} {dx} &=\ cos x\\ [4pt]
\ dfrac {d^2y} {dx^2} &=−\ sin x\\ [4pt]
\ dfrac {d^3y} {dx^3} &=− cos\ x\\ [4pt]]
\ dfrac {d^4y} {dx^4} &=\ sin x\ end {align*}\]
Análise
Depois de reconhecermos o padrão das derivadas, podemos encontrar qualquer derivada de ordem superior determinando a etapa no padrão ao qual ela corresponde. Por exemplo, cada quarta derivada de\(\sin x\) igual é igual\(\sin x\), então
\[\dfrac{d^4}{dx^4}(\sin x)=\dfrac{d^8}{dx^8}(\sin x)=\dfrac{d^{12}}{dx^{12}}(\sin x)=…=\dfrac{d^{4n}}{dx^{4n}}(\sin x)=\sin x \nonumber \]
\[\dfrac{d^5}{dx^5}(\sin x)=\dfrac{d^9}{dx^9}(\sin x)=\dfrac{d^{13}}{dx^{13}}(\sin x)=…=\dfrac{d^{4n+1}}{dx^{4n+1}}(\sin x)=\cos x. \nonumber \]
Para\(y=\cos x\), encontre\(\dfrac{d^4y}{dx^4}\).
- Dica
-
Veja o exemplo anterior.
- Responda
-
\(\cos x\)
Encontre\(\dfrac{d^{74}}{dx^{74}}(\sin x)\).
Solução
Podemos ver imediatamente que, para a 74ª derivada de\(\sin x\),\(74=4(18)+2\), então
\[\dfrac{d^{74}}{dx^{74}}(\sin x)=\dfrac{d^{72+2}}{dx^{72+2}}(\sin x)=\dfrac{d^2}{dx^2}(\sin x)=−\sin x. \nonumber \]
Para\(y=\sin x\), encontre\(\dfrac{d^{59}}{dx^{59}}(\sin x).\)
- Dica
-
\(\dfrac{d^{59}}{dx^{59}}(\sin x)=\dfrac{d^{4⋅14+3}}{dx^{4⋅14+3}}(\sin x)\)
- Responda
-
\(−\cos x\)
Uma partícula se move ao longo de um eixo coordenado de tal forma que sua posição no tempo\(t\) é dada por\(s(t)=2−\sin t\). Encontre\(v(π/4)\)\(a(π/4)\) e. Compare esses valores e decida se a partícula está acelerando ou diminuindo a velocidade.
Solução
Primeiro achado\(v(t)=s′(t)\)
\[v(t)=s′(t)=−\cos t . \nonumber \]
Assim,
\(v\left(\frac{π}{4}\right)=−\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\).
Em seguida, encontre\(a(t)=v′(t)\). Assim,\(a(t)=v′(t)=\sin t\) e nós temos
\(a\left(\frac{π}{4}\right)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\).
Desde\(v\left(\frac{π}{4}\right)=−\dfrac{\sqrt{2}}{2}<0\) e\(a\left(\frac{π}{4}\right)=\dfrac{\sqrt{2}}{2}>0\), vemos que a velocidade e a aceleração estão agindo em direções opostas; ou seja, o objeto está sendo acelerado na direção oposta à direção em que está viajando. Consequentemente, a partícula está ficando mais lenta.
Um bloco preso a uma mola está se movendo verticalmente. Sua posição no momento t é dada por\(s(t)=2\sin t\). Encontre\(v\left(\frac{5π}{6}\right)\)\(a\left(\frac{5π}{6}\right)\) e. Compare esses valores e decida se o bloqueio está acelerando ou diminuindo a velocidade.
- Dica
-
Use o exemplo\(\PageIndex{9}\) como guia.
- Responda
-
\(v\left(\frac{5π}{6}\right)=−\sqrt{3}<0\)\(a\left(\frac{5π}{6}\right)=−1<0\)e. O quarteirão está acelerando.
Conceitos-chave
- Podemos encontrar as derivadas de\(\sin x\) e\(\cos x\) usando a definição de derivada e as fórmulas de limite encontradas anteriormente. Os resultados são
\(\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big)=−\sin x\).
- Com essas duas fórmulas, podemos determinar as derivadas de todas as seis funções trigonométricas básicas.
Equações-chave
- Derivada da função senoidal
\(\dfrac{d}{dx}(\sin x)=\cos x\)
- Derivada da função cosseno
\(\dfrac{d}{dx}(\cos x)=−\sin x\)
- Derivada da função tangente
\(\dfrac{d}{dx}(\tan x )=\sec^2x\)
- Derivada da função cotangente
\(\dfrac{d}{dx}(\cot x )=−\csc^2x\)
- Derivada da função secante
\(\dfrac{d}{dx}(\sec x)=\sec x\tan x \)
- Derivada da função cossecante
\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x \)


