3.5E: Exercícios para a Seção 3.5

Last updated
Save as PDF

Page ID: 188440

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 10, encontre$\dfrac{dy}{dx}$ as funções dadas.

1)$y=x^2−\sec x+1$

Responda: $\dfrac{dy}{dx}=2x−\sec x\tan x$

2)$y=3\csc x+\dfrac{5}{x}$

3)$y=x^2\cot x$

Responda: $\dfrac{dy}{dx}=2x\cot x−x^2\csc^2 x$

4)$y=x−x^3\sin x$

5)$y=\dfrac{\sec x}{x}$

Responda: $\dfrac{dy}{dx}=\dfrac{x\sec x\tan x−\sec x}{x^2}$

6)$y=\sin x\tan x$

7)$y=(x+\cos x)(1−\sin x)$

Responda: $\dfrac{dy}{dx}=(1−\sin x)(1−\sin x)−\cos x(x+\cos x)$

8)$y=\dfrac{\tan x}{1−\sec x}$

9)$y=\dfrac{1−\cot x}{1+\cot x}$

Responda: $\dfrac{dy}{dx}=\dfrac{2\csc^2 x}{(1+\cot x)^2}$

10)$y=(\cos x)(1+\csc x)$

Nos exercícios 11 a 16, encontre a equação da reta tangente a cada uma das funções dadas nos valores indicados de$x$. Em seguida, use uma calculadora para representar graficamente a função e a reta tangente para garantir que a equação da reta tangente esteja correta.

11) [T]$f(x)=−\sin x,\quad x=0$

Responda

$y=−x$

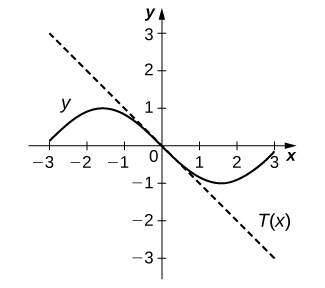
$O gráfico mostra menos sin (x) e a linha reta T (x) com inclinação −1 e y intercepto 0.$

12) [T]$f(x)=\csc x,\quad x=\frac{π}{2}$

13) [T]$f(x)=1+\cos x,\quad x=\frac{3π}{2}$

Responda

$y=x+\frac{2−3π}{2}$

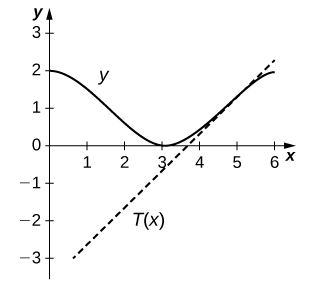
$O gráfico mostra a função cosseno deslocada um para cima e tem a linha reta T (x) com inclinação 1 e intercepto y (2 — 3π) /2.$

14) [T]$f(x)=\sec x,\quad x=\frac{π}{4}$

15) [T]$f(x)=x^2−\tan x, \quad x=0$

Responda

$y=−x$

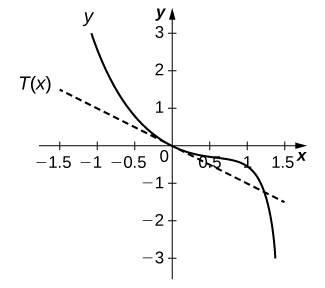
$O gráfico mostra a função começando em (−1, 3), diminuindo até a origem, continuando a diminuir lentamente para cerca de (1, −0,5), ponto em que ela diminui muito rapidamente.$

16) [T]$f(x)=5\cot x, \quad x=\frac{π}{4}$

Nos exercícios 17 a 22, encontre$\dfrac{d^2y}{dx^2}$ as funções dadas.

17)$y=x\sin x−\cos x$

Responda: $\dfrac{d^2y}{dx^2} = 3\cos x−x\sin x$

18)$y=\sin x\cos x$

19)$y=x−\frac{1}{2}\sin x$

Responda: $\dfrac{d^2y}{dx^2} = \frac{1}{2}\sin x$

20)$y=\dfrac{1}{x}+\tan x$

21)$y=2\csc x$

Responda: $\dfrac{d^2y}{dx^2} = 2\csc(x)\left(\csc^2(x)+\cot^2(x)\right) $

22)$y=\sec^2 x$

23) Encontre todos os$x$ valores no gráfico de$f(x)=−3\sin x\cos x$ onde a reta tangente é horizontal.

Responda: $x = \dfrac{(2n+1)π}{4}$, onde$n$ é um número inteiro

24) Encontre todos os$x$ valores no gráfico de$f(x)=x−2\cos x$ para$0<x<2π$ onde a reta tangente tem inclinação 2.

25) Vamos$f(x)=\cot x.$ determinar os pontos no gráfico de$f$ para$0<x<2π$ onde a (s) reta (s) tangente (s) é (são) paralela (s) à linha$y=−2x$.

Responda: $\left(\frac{π}{4},1\right),\quad \left(\frac{3π}{4},−1\right),\quad\left(\frac{5π}{4},1\right),\quad \left(\frac{7π}{4},−1\right)$

26) [T] Uma massa em uma mola salta para cima e para baixo em um movimento harmônico simples, modelado pela função em$s(t)=−6\cos t$ que s é medido em polegadas e$t$ é medido em segundos. Encontre a taxa na qual a mola está oscilando em$t=5$ s.

27) Deixe a posição de um pêndulo giratório em movimento harmônico simples ser dada por$s(t)=a\cos t+b\sin t$. Encontre as constantes$a$ e de$b$ forma que quando a velocidade for de 3 cm/s,$s=0$$t=0$ e.

Responda: $a=0,\quad b=3$

28) Depois que um mergulhador pula de uma prancha de mergulho, a borda da prancha oscila com a posição dada por$s(t)=−5\cos t$ cm$t$ segundos após o salto.

a. Esboce um período da função de posição para$t≥0$.

b. Encontre a função de velocidade.

c. Esboce um período da função de velocidade para$t≥0$.

d. Determine os momentos em que a velocidade$0$ ultrapassa um período.

e. Encontre a função de aceleração.

f. Esboce um período da função de aceleração para$t≥0$.

29) O número de hambúrgueres vendidos em um restaurante de fast-food em Pasadena, Califórnia, é dado por$y=10+5\sin x$ onde$y$ está o número de hambúrgueres vendidos e$x$ representa o número de horas após a abertura do restaurante, das 11h às 23h, quando a loja fecha. Encontre$y'$ e determine os intervalos em que o número de hambúrgueres vendidos está aumentando.

Responda: $y′=5\cos(x)$, aumentando em$\left(0,\frac{π}{2}\right),\;\left(\frac{3π}{2},\frac{5π}{2}\right)$ e$\left(\frac{7π}{2},12\right)$

30) [T] A quantidade de chuvas por mês em Phoenix, Arizona, pode ser aproximada em$y(t)=0.5+0.3\cos t$, onde$t$ estão meses desde janeiro. Encontre$y′$ e use uma calculadora para determinar os intervalos em que a quantidade de chuva caindo está diminuindo.

Para os exercícios 31 a 33, use a regra do quociente para derivar as equações dadas.

31)$\dfrac{d}{dx}(\cot x)=−\csc^2x$

32)$\dfrac{d}{dx}(\sec x)=\sec x\tan x$

33)$\dfrac{d}{dx}(\csc x)=−\csc x\cot x$

34) Use a definição de derivado e a identidade$\cos(x+h)=\cos x\cos h−\sin x\sin h$ para provar isso$\dfrac{d}{dx}(\cos x)=−\sin x$.

Para os exercícios 35 a 39, encontre a derivada de ordem superior solicitada para as funções dadas.

35)$\dfrac{d^3y}{dx^3}$ do$y=3\cos x$

Resposta: $\dfrac{d^3y}{dx^3} = 3\sin x$

36)$\dfrac{d^2y}{dx^2}$ do$y=3\sin x+x^2\cos x$

37)$\dfrac{d^4y}{dx^4}$ do$y=5\cos x$

Resposta: $\dfrac{d^4y}{dx^4} = 5\cos x$

38)$\dfrac{d^2y}{dx^2}$ do$y=\sec x+\cot x$

39)$\dfrac{d^3y}{dx^3}$ do$y=x^{10}−\sec x$

Resposta: $\dfrac{d^3y}{dx^3} = 720x^7−5\tan(x)\sec^3(x)−\tan^3(x)\sec(x)$