3.4E: Exercícios para a Seção 3.4

Last updated
Save as PDF

Page ID: 188481

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 3, as funções dadas representam a posição de uma partícula viajando ao longo de uma linha horizontal.

a. Encontre as funções de velocidade e aceleração.

b. Determine os intervalos de tempo em que o objeto está diminuindo ou acelerando.

1)$s(t)=2t^3−3t^2−12t+8$

2)$s(t)=2t^3−15t^2+36t−10$

Resposta: a.$v(t)=6t^2−30t+36,\quad a(t)=12t−30$;
b. acelera para$ (2,2.5)∪(3,∞)$, desacelera para$(0,2)∪(2.5,3)$

3)$s(t)=\dfrac{t}{1+t^2}$

4) Um foguete é disparado verticalmente para cima a partir do solo. A distância$s$ em pés que o foguete percorre do solo após$t$ segundos é dada por$s(t)=−16t^2+560t$.

a. Determine a velocidade do foguete 3 segundos após ser disparado.

b. Encontre a aceleração do foguete 3 segundos após ser disparado.

Responda: a.$464\; \text{ft/s}^2$
b.$−32\;\text{ft/s}^2$

5) Uma bola é lançada para baixo com uma velocidade de 8 pés/s do topo de um prédio de 64 pés de altura. Depois de$t$ segundos, sua altura acima do solo é dada por$s(t)=−16t^2−8t+64.$

a. Determine quanto tempo a bola leva para atingir o chão.

b. Determine a velocidade da bola quando ela atinge o chão.

6) A função de posição$s(t)=t^2−3t−4$ representa a posição da parte traseira de um carro saindo da garagem e depois dirigindo em linha reta, em$s$ pés e$t$ em segundos. Nesse caso,$s(t)=0$ representa o tempo em que a traseira do carro está na porta da garagem, assim$s(0)=−4$ como a posição inicial do carro, 4 pés dentro da garagem.

a. Determine a velocidade do carro quando$s(t)=0$.

b. Determine a velocidade do carro quando$s(t)=14$.

Responda: a.$5$
pés/b.$9$ pés/s

7) A posição de um beija-flor voando em linha reta em$t$ segundos é dada em$s(t)=3t^3−7t$ metros.

a. Determine a velocidade da ave em$t=1$ segundos.

b. Determine a aceleração do pássaro em$t=1$ segundos.

c. Determine a aceleração da ave quando a velocidade for igual a 0.

8) Uma batata é lançada verticalmente para cima com uma velocidade inicial de 100 pés/s de uma pistola de batata no topo de um prédio de 85 pés de altura. A distância em pés que a batata percorre do solo após$t$ segundos é dada por$s(t)=−16t^2+100t+85$.

a. Determine a velocidade da batata depois de$0.5$$5.75$ s e s.

b. Encontre a velocidade da batata em$0.5$$5.75$ s e s.

c. Determine quando a batata atinge sua altura máxima.

d. Encontre a aceleração da batata em$0.5$$1.5$ s e s.

e. Determine quanto tempo a batata está no ar.

f. Determine a velocidade da batata ao atingir o solo.

Responda: a. 84 pés/s, −84
pés/b. 84
pés/c.$\frac{25}{8}$ s
d.$−32 \; \text{ft/s}^2$ em ambos os casos
e.$\frac{1}{8}(25+\sqrt{965})$ s
f.$−4\sqrt{965}$ ft/s

9) A função de posição$s(t)=t^3−8t$ fornece a posição em milhas de um trem de carga, onde o leste é a direção positiva e$t$ é medido em horas.

a. Determine a direção em que o trem está viajando$s(t)=0$.

b. Determine a direção em que o trem está viajando$a(t)=0$.

c. Determine os intervalos de tempo em que o trem está desacelerando ou acelerando.

10) O gráfico a seguir mostra a posição$y=s(t)$ de um objeto se movendo ao longo de uma linha reta.

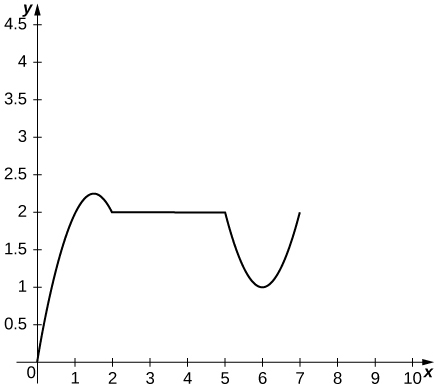
$No plano de coordenadas cartesianas, é representada graficamente uma função que faz parte de uma parábola da origem até (2, 2) com máximo em (1,5, 2,25). Então, a função é constante até (5, 2), em que os pontos se tornam uma parábola novamente, diminuindo ao mínimo em (6, 1) e depois aumentando para (7, 2).$

a. Use o gráfico da função de posição para determinar os intervalos de tempo em que a velocidade é positiva, negativa ou zero.

b. Esboce o gráfico da função de velocidade.

c. Use o gráfico da função de velocidade para determinar os intervalos de tempo em que a aceleração é positiva, negativa ou zero.

d. Determine os intervalos de tempo em que o objeto está acelerando ou diminuindo a velocidade.

Responda

a. A velocidade é positiva ligada$(0,1.5)∪(6,7)$, negativa ligada$(1.5,2)∪(5,6)$ e zero ligada$(2,5)$.

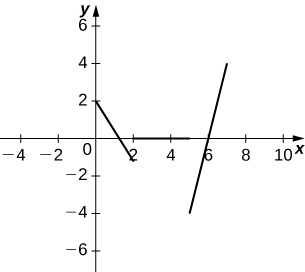
$O gráfico é uma linha reta de (0, 2) a (2, −1), depois é descontínuo com uma linha reta de (2, 0) a (5, 0) e, em seguida, é descontínuo com uma linha reta de (5, −4) a (7, 4).$

c. A aceleração é positiva ligada$(5,7)$, negativa$(0,2)$ ligada e zero ligada$(2,5)$.
d. O objeto está acelerando$(6,7)∪(1.5,2)$ e diminuindo a velocidade$(0,1.5)∪(5,6)$.

11) A função de custo, em dólares, de uma empresa que fabrica processadores de alimentos é dada por$C(x)=200+\dfrac{7}{x}+\dfrac{x}{27}$, onde$x$ está o número de processadores de alimentos fabricados.

a. Encontre a função de custo marginal.

b. Encontre o custo marginal de fabricação de 12 processadores de alimentos.

c. Encontre o custo real de fabricação do décimo terceiro processador de alimentos.

12) O preço p (em dólares) e a demanda$x$ por um determinado rádio-relógio digital são dados pela função preço-demanda$p=10−0.001x$.

a. Encontre a função de receita$R(x)$

b. Encontre a função de receita marginal.

c. Encontre a receita marginal em$x=2000$$5000$ e.

Responda: a.$R(x)=10x−0.001x^2$
b.$ R′(x)=10−0.002x$
c. $6 por item, $0 por item

13) [T] Um lucro é obtido quando a receita excede o custo. Suponha que a função de lucro de um fabricante de skates seja dada por$P(x)=30x−0.3x^2−250$, onde$x$ está o número de skates vendidos.

a. Encontre o lucro exato da venda do trigésimo skate.

b. Encontre a função de lucro marginal e use-a para estimar o lucro da venda do trigésimo skate.

14) [T] Em geral, a função de lucro é a diferença entre as funções de receita e custo:$P(x)=R(x)−C(x)$.

Suponha que as funções de preço-demanda e custo para a produção de furadeiras sem fio sejam dadas respectivamente por$p=143−0.03x$ e$C(x)=75,000+65x$, onde$x$ está o número de furadeiras sem fio que são vendidas a um preço de$p$ dólares por furadeira e$C(x)$ é o custo de produção de furadeiras$x$ sem fio.

a. Encontre a função de custo marginal.

b. Encontre as funções de receita e receita marginal.

c. Encontre$R′(1000)$$R′(4000)$ e. Interprete os resultados.

d. Encontre as funções de lucro e lucro marginal.

e. Encontre$P′(1000)$$P′(4000)$ e. Interprete os resultados.

Responda: a.$C′(x)=65$
b.$R(x)=143x−0.03x^2$,$R′(x)=143−0.06x$
$R′(1000)=83, \quad R′(4000) = −97$ c. Em um nível de produção de 1000 furadeiras sem fio, a receita está aumentando a uma taxa de $83 por furadeira; em um nível de produção de 4.000 furadeiras sem fio, a receita está diminuindo a uma taxa de $97 por furadeira.
d.$P(x)=−0.03x^2+78x−75000, \quad P′(x)=−0.06x+78$
$P′(1000)=18, \quad P′(4000) =−162$ e. Em um nível de produção de 1000 furadeiras sem fio, o lucro está aumentando a uma taxa de $18 por furadeira; em um nível de produção de 4000 furadeiras sem fio, o lucro está diminuindo a uma taxa de $162 por furadeira.

15) Uma pequena cidade em Ohio contratou uma empresa atuarial para realizar um estudo que modelou a taxa de mudança da população da cidade. O estudo descobriu que a população da cidade (medida em milhares de pessoas) pode ser modelada pela função$P(t)=−\frac{1}{3}t^3+64t+3000$, onde$t$ é medida em anos.

a. Encontre a função de taxa de variação$P′(t)$ da função de população.

b. Encontre$P′(1),\; P′(2),\; P′(3)$,$P′(4)$ e. Interprete o que os resultados significam para a cidade.

c. Encontre$P''(1),\; P''(2),\; P''(3)$,$P''(4)$ e. Interprete o que os resultados significam para a população da cidade.

16) [T] Uma cultura de bactérias cresce em número de acordo com a função$N(t)=3000(1+\dfrac{4t}{t^2+100})$, onde$t$ é medida em horas.

a. Encontre a taxa de variação do número de bactérias.

b. Encontre$N′(0),\; N′(10),\; N′(20)$,$N′(30)$ e.

c. Interprete os resultados em (b).

d. Encontre$N''(0),\; N''(10),\; N''(20),$$N''(30)$ e. Interprete o que as respostas sugerem sobre o crescimento populacional de bactérias.

Responda: a.$N′(t)=3000\left(\dfrac{−4t^2+400}{(t^2+100)^2}\right)$
b.$120,0,−14.4,−9.6$
c. A população de bactérias aumenta de 0 a 10 horas; depois, a população de bactérias diminui.
$0,−6,0.384,0.432$d. A taxa na qual a bactéria está aumentando está diminuindo durante as primeiras 10 horas. Posteriormente, a população de bactérias está diminuindo a uma taxa decrescente.

17) A força centrípeta de um objeto de massa m é dada por$F(r)=\dfrac{mv^2}{r}$, onde$v$ é a velocidade de rotação e$r$ é a distância do centro de rotação.

a. Determine a taxa de variação da força centrípeta em relação à distância do centro de rotação.

b. Encontre a taxa de variação da força centrípeta de um objeto com massa de 1000 kg, velocidade de 13,89 m/s e distância do centro de rotação de 200 metros.

As questões a seguir dizem respeito à população (em milhões) de Londres por década no século XIX, que está listada na tabela a seguir.

Ano desde 1800	População (milhões)
1	0,8975
11	1,040
21	1.264
31	1,516
41	1.661
51	2.000
61	2.634
71	3.272
81	3.911
91	4.422

População de LondresFonte: http://en.Wikipedia.org/wiki/Demographics_of_London

18) [T]

a. Usando uma calculadora ou um programa de computador, encontre a função linear mais adequada para medir a população.

b. Encontre a derivada da equação em a. e explique seu significado físico.

c. Encontre a segunda derivada da equação e explique seu significado físico.

Responda: a.$P(t)=0.03983+0.4280$
$P′(t)=0.03983$ b. A população está aumentando.
$P''(t)=0$c. A taxa na qual a população está aumentando é constante.

19) [T]

a. Usando uma calculadora ou um programa de computador, encontre a curva quadrática mais adequada por meio dos dados.

b. Encontre a derivada da equação e explique seu significado físico.

c. Encontre a segunda derivada da equação e explique seu significado físico.

Para os exercícios a seguir, considere um astronauta em um grande planeta em outra galáxia. Para saber mais sobre a composição desse planeta, o astronauta joga um sensor eletrônico em uma trincheira profunda. O sensor transmite sua posição vertical a cada segundo em relação à posição do astronauta. O resumo dos dados do sensor de queda é exibido na tabela a seguir.

Tempo após a queda (s)	Posição (m)
0	0
1	−1
2	−2
3	−5
4	−7
5	−14

20) [T]

a. Usando uma calculadora ou um programa de computador, encontre a curva quadrática mais adequada aos dados.

b. Encontre a derivada da função de posição e explique seu significado físico.

c. Encontre a segunda derivada da função de posição e explique seu significado físico.

Responda: a.$p(t)=−0.6071x^2+0.4357x−0.3571$
$p′(t)=−1.214x+0.4357$ b. Essa é a velocidade do sensor.
$p''(t)=−1.214$c. Essa é a aceleração do sensor; é uma aceleração constante para baixo.

21) [T]

a. Usando uma calculadora ou um programa de computador, encontre a curva cúbica mais adequada aos dados.

b. Encontre a derivada da função de posição e explique seu significado físico.

c. Encontre a segunda derivada da função de posição e explique seu significado físico.

d. Usando o resultado de c. explique por que uma função cúbica não é uma boa escolha para esse problema.

Os problemas a seguir lidam com as equações de Holling tipo I, II e III. Essas equações descrevem o evento ecológico de crescimento de uma população de predadores, dada a quantidade de presas disponíveis para consumo.

22) [T] A equação Holling tipo I é descrita por$f(x)=ax$, onde$x$ está a quantidade de presas disponível e$a>0$ é a taxa na qual o predador encontra a presa para consumo.

a. Representa graficamente a equação de Holling tipo I, dada$a=0.5$.

b. Determine a primeira derivada da equação de Holling tipo I e explique fisicamente o que a derivada implica.

c. Determine a segunda derivada da equação de Holling tipo I e explique fisicamente o que a derivada implica.

d. Usando as interpretações de b. e c. explique por que a equação de Holling tipo I pode não ser realista.

Responda

uma.

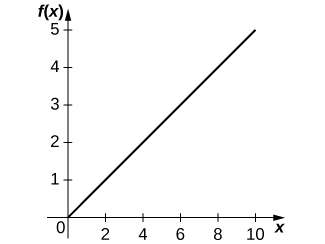
$O gráfico é uma linha reta traçada através da origem com inclinação 1/2.$

$f′(x)=a$b. Quanto maior o aumento de presas, maior o crescimento dos predadores.
$f''(x)=0$c. À medida que a quantidade de presas aumenta, a taxa na qual o crescimento da população de predadores aumenta é constante.
d. Essa equação pressupõe que, se houver mais presas, o predador é capaz de aumentar o consumo linearmente. Essa suposição não é física porque esperaríamos que houvesse algum ponto de saturação no qual haja muita presa para o predador consumir adequadamente.

23) [T] A equação Holling tipo II é descrita por$f(x)=\dfrac{ax}{n+x}$, onde$x$ está a quantidade de presas disponível e$a>0$ é a taxa máxima de consumo do predador.

a. Faça um gráfico da equação de Holling tipo II dada$a=0.5$$n=5$ e. Quais são as diferenças entre as equações de Holling tipo I e II?

b. Pegue a primeira derivada da equação de Holling tipo II e interprete o significado físico da derivada.

c.$f(n)=\frac{1}{2}a$ Mostre isso e interprete o significado do parâmetro n.

d. Encontre e interprete o significado da segunda derivada. O que torna a função Holling tipo II mais realista do que a função Holling tipo I?

24) [T] A equação Holling tipo III é descrita por$f(x)=\dfrac{ax^2}{n^2+x^2}$, onde x é a quantidade de presa disponível e$a>0$ é a taxa máxima de consumo do predador.

a. Representar graficamente a equação de Holling tipo III dada$a=0.5$ e$n=5.$ quais são as diferenças entre as equações de Holling tipo II e III?

b. Pegue a primeira derivada da equação de Holling tipo III e interprete o significado físico da derivada.

c. Encontre e interprete o significado da segunda derivada (pode ajudar a representar graficamente a segunda derivada).

d. Quais fenômenos ecológicos adicionais a função Holling tipo III descreve em comparação com a função Holling tipo II?

Responda

uma.

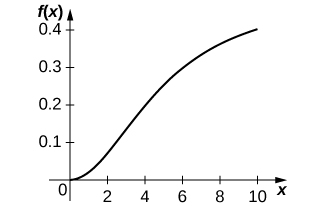
$O gráfico aumenta da origem rapidamente no início e depois lentamente para (10, 0,4).$

$f′(x)=\dfrac{2axn^2}{(n^2+x^2)^2}$b. Quando a quantidade de presas aumenta, o crescimento do predador aumenta.
$f''(x)=\dfrac{2an^2(n^2−3x^2)}{(n^2+x^2)^3}$c. Quando a quantidade de presas é extremamente pequena, a taxa na qual o crescimento do predador está aumentando está aumentando, mas quando a quantidade de presas atinge acima de um certo limite, a taxa na qual o crescimento do predador está aumentando começa a diminuir.
d. Em níveis mais baixos de presas, a presa é mais facilmente capaz de evitar a detecção pelo predador, portanto, menos presas são consumidas, resultando em menos crescimento de predadores.

25) [T] As populações da lebre com raquetes de neve (em milhares) e do lince (em centenas) coletadas ao longo de 7 anos, de 1937 a 1943, são mostradas na tabela a seguir. A lebre com raquetes de neve é a principal presa do lince.

População de lebres com raquetes de neve (milhares)	População de lince (centenas)
20	10
5	15
65	55
95	60

Populações de lebres e linces com raquetes de neve Fonte: http://www.biotopics.co.uk/newgcse/predatorprey.html.

a. Faça um gráfico dos pontos de dados e determine qual função do tipo Holling se ajusta melhor aos dados.

b. Usando os significados dos parâmetros$a$ e$n$, determine os valores desses parâmetros examinando um gráfico dos dados. Lembre-se de que$n$ mede qual valor da presa resulta na metade máxima do valor do predador.

c. Faça um gráfico das funções resultantes do tipo Holling I, II e III sobre os dados. O resultado da parte a. estava correto?