3.4: Derivativos como taxas de variação

Objetivos de

• Determine um novo valor de uma quantidade a partir do valor antigo e do valor da alteração.
• Calcule a taxa média de variação e explique como ela difere da taxa de variação instantânea.
• Aplique taxas de alteração ao deslocamento, velocidade e aceleração de um objeto se movendo ao longo de uma linha reta.
• Preveja a população futura a partir do valor atual e da taxa de crescimento populacional.
• Use derivativos para calcular o custo marginal e a receita em uma situação comercial.

Nesta seção, examinamos algumas aplicações da derivada, focando na interpretação da derivada como a taxa de variação de uma função. Essas aplicações incluem aceleração e velocidade na física, taxas de crescimento populacional em biologia e funções marginais em economia.

Fórmula de quantidade de alteração

Uma aplicação para derivadas é estimar um valor desconhecido de uma função em um ponto usando um valor conhecido de uma função em algum ponto determinado junto com sua taxa de variação em um determinado ponto. Se$f(x)$ for uma função definida em um intervalo$[a,a+h]$, então a quantidade de mudança de$f(x)$ ao longo do intervalo é a mudança nos$y$ valores da função nesse intervalo e é dada por

$$f(a+h)−f(a). \nonumber$$

A taxa média de mudança da função$f$ nesse mesmo intervalo é a razão entre a quantidade de mudança nesse intervalo e a alteração correspondente nos$x$ valores. É dado por

$$\frac{f(a+h)−f(a)}{h}. \nonumber$$

Como já sabemos, a taxa instantânea de variação de$f(x)$ at$a$ é sua derivada

$$f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \nonumber$$

Para valores suficientemente pequenos de$h$,$f′(a)≈\frac{f(a+h)−f(a)}{h}$. Em seguida, podemos resolver$f(a+h)$ para obter a fórmula da quantidade de mudança:

$$f(a+h)≈f(a)+f′(a)h. \label{linapprox}$$

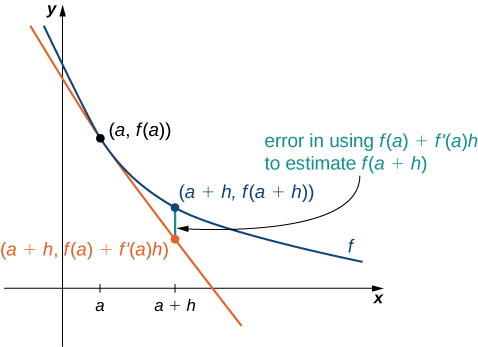
Podemos usar essa fórmula se soubermos apenas$f(a)$$f′(a)$ e quisermos estimar o valor de$f(a+h)$. Por exemplo, podemos usar a população atual de uma cidade e a taxa na qual ela está crescendo para estimar sua população em um futuro próximo. Como podemos ver na Figura$\PageIndex{1}$, estamos nos aproximando$f(a+h)$ pela$y$ coordenada em a+h na reta tangente a$f(x)$ at$x=a$. Observe que a precisão dessa estimativa depende do valor de$h$, bem como do valor de$f′(a)$.

Figura$\PageIndex{1}$: O novo valor de uma quantidade alterada é igual ao valor original mais a taxa de alteração multiplicada pelo intervalo de alteração:$f(a+h)≈f(a)+f′(a)h.$

Exemplo$\PageIndex{1}$: Estimating the Value of a Function

Se$f(3)=2$ e$f′(3)=5$, estime$f(3.2)$.

Solução

Comece encontrando$h$. Nós temos$h=3.2−3=0.2.$ assim,

$f(3.2)=f(3+0.2)≈f(3)+(0.2)f′(3)=2+0.2(5)=3.$

Exercício$\PageIndex{1}$

Dado$f(10)=−5$ e$f′(10)=6$, estime$f(10.1)$.

Dica

Use o mesmo processo do exemplo anterior.

Responda

$−4.4$

Movimento ao longo de uma linha

Outro uso da derivada é analisar o movimento ao longo de uma linha. Descrevemos a velocidade como a taxa de mudança de posição. Se tomarmos a derivada da velocidade, podemos encontrar a aceleração ou a taxa de variação da velocidade. Também é importante introduzir a ideia de velocidade, que é a magnitude da velocidade. Assim, podemos afirmar as seguintes definições matemáticas.

Definição

$s(t)$Seja uma função que fornece a posição de um objeto no tempo t.

• A velocidade do objeto no momento$t$ é dada por$v(t)=s′(t)$.
• A velocidade do objeto no momento$t$ é dada por$|v(t)|$.
• A aceleração do objeto em$t$ é dada por$a(t)=v′(t)=s''(t)$.

Exemplo$\PageIndex{2}$: Comparing Instantaneous Velocity and Average Velocity

Uma bola cai de uma altura de 64 pés. Sua altura acima do solo (em pés)$t$ segundos depois é dada por$s(t)=−16t^2+64$.

1. Qual é a velocidade instantânea da bola quando ela atinge o chão?
2. Qual é a velocidade média durante sua queda?

Solução

A primeira coisa a fazer é determinar quanto tempo a bola leva para chegar ao chão. Para fazer isso, defina$s(t)=0$. Resolvendo$−16t^2+64=0$, obtemos$t=2$, então leva 2 segundos para a bola chegar ao chão.

1. A velocidade instantânea da bola quando ela atinge o chão é$v(2)$. Desde então$v(t)=s′(t)=−32t$, obtemos$v(t)=−64$ pés/s.
2. A velocidade média da bola durante sua queda é

$v_{ave}=\frac{s(2)−s(0)}{2−0}=\frac{0−64}{2}=−32$pés/s.

Exemplo$\PageIndex{3}$: Interpreting the Relationship between $v(t)$ and $a(t)$

Uma partícula se move ao longo de um eixo coordenado na direção positiva para a direita. Sua posição no momento$t$ é dada por$s(t)=t^3−4t+2$. Encontre$v(1)$$a(1)$ e use esses valores para responder às seguintes perguntas.

1. A partícula está se movendo da esquerda para a direita ou da direita para a esquerda no momento$t=1$?
2. A partícula está acelerando ou diminuindo de vez em quando$t=1$?

Solução

Comece encontrando$v(t)$$a(t)$ e.

$v(t) = s'(t) = 3t^2 - 4$$a(t)=v′(t)=s''(t)=6t$e.

Avaliando essas funções em$t=1$, obtemos$v(1)=−1$$a(1)=6$ e.

1. Porque$v(1)<0$ a partícula está se movendo da direita para a esquerda.
2. Porque$v(1)<0$ e$a(1)>0$, a velocidade e a aceleração estão agindo em direções opostas. Em outras palavras, a partícula está sendo acelerada na direção oposta à direção em que está viajando, fazendo com que$|v(t)|$ diminua. A partícula está diminuindo.

Exemplo$\PageIndex{4}$: Position and Velocity

A posição de uma partícula se movendo ao longo de um eixo coordenado é dada por$s(t)=t^3−9t^2+24t+4,\; t≥0.$

1. Encontre$v(t)$.
2. Em que momento (s) a partícula está em repouso?
3. Em quais intervalos de tempo a partícula está se movendo da esquerda para a direita? Da direita para a esquerda?
4. Use as informações obtidas para esboçar o caminho da partícula ao longo de um eixo coordenado.

Solução

a. A velocidade é a derivada da função de posição:

$v(t)=s′(t)=3t^2−18t+24.$

b. A partícula está em repouso quando$v(t)=0$, assim definida$3t^2−18t+24=0$. Fatorar o lado esquerdo da equação produz$3(t−2)(t−4)=0$. Resolvendo, descobrimos que a partícula está em repouso em$t=2$$t=4$ e.

c. A partícula está se movendo da esquerda para a direita quando$v(t)>0$ e da direita para a esquerda quando$v(t)<0$. A figura$\PageIndex{2}$ fornece a análise do sinal de$v(t)$ for$t≥0$, mas não representa o eixo ao longo do qual a partícula está se movendo.

Figura: O$\PageIndex{2}$ sinal de determina$v(t)$ a direção da partícula.

• Desde então$3t^2−18t+24>0$$[0,2)∪(4,+∞)$, a partícula está se movendo da esquerda para a direita nesses intervalos.
• Desde então$3t^2−18t+24<0$$(2,4)$, a partícula está se movendo da direita para a esquerda nesse intervalo.

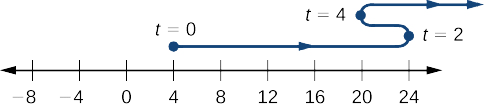
d. Antes de podermos esboçar o gráfico da partícula, precisamos saber sua posição no momento em que ela começa a se mover$(t=0)$ e nos momentos em que muda de direção$(t=2,4)$. Nós temos$s(0)=4$$s(2)=24$,$s(4)=20$ e. Isso significa que a partícula começa no eixo coordenado em$4$ e muda de direção no$24$ e$20$ sobre o eixo coordenado. O caminho da partícula é mostrado em um eixo de coordenadas na Figura$\PageIndex{3}$.

Figura$\PageIndex{3}$: O caminho da partícula pode ser determinado pela análise$v(t)$.

Exercício$\PageIndex{2}$

Uma partícula se move ao longo de um eixo coordenado. Sua posição no momento$t$ é dada por$s(t)=t^2−5t+1$. A partícula está se movendo da direita para a esquerda ou da esquerda para a direita no momento$t=3$?

Dica

Encontre$v(3)$ e veja a placa.

Responda

da esquerda para a direita

Mudança populacional

Além de analisar velocidade, velocidade, aceleração e posição, podemos usar derivados para analisar vários tipos de populações, incluindo aquelas tão diversas quanto colônias de bactérias e cidades. Podemos usar uma população atual, junto com uma taxa de crescimento, para estimar o tamanho de uma população no futuro. A taxa de crescimento populacional é a taxa de mudança de uma população e, consequentemente, pode ser representada pela derivada do tamanho da população.

Definição

Se$P(t)$ for o número de entidades presentes em uma população, então a taxa de crescimento populacional de$P(t)$ é definida como$P′(t)$.

Exemplo$\PageIndex{5}$: Estimating a Population

A população de uma cidade está triplicando a cada 5 anos. Se sua população atual for de 10.000, qual será sua população aproximada daqui a 2 anos?

Solução

$P(t)$Seja a população (em milhares)$t$ daqui a alguns anos. Assim, sabemos disso$P(0)=10$ e, com base nas informações, antecipamos$P(5)=30$. Agora$P′(0)$, estime, a taxa de crescimento atual, usando

$P′(0)≈\frac{P(5)−P(0)}{5−0}=\frac{30−10}{5}=4$.

Ao aplicar a Equação\ ref {linapprox} a$P(t)$, podemos estimar a população daqui a 2 anos escrevendo

$P(2)≈P(0)+(2)P′(0)≈10+2(4)=18$;

assim, em 2 anos, a população será de 18.000.

Exercício$\PageIndex{3}$

Sabe-se que a população atual de uma colônia de mosquitos é de 3.000; ou seja,$P(0)=3,000$. Se$P′(0)=100$, estime o tamanho da população em 3 dias, onde$t$ é medido em dias.

Dica

Use$P(3)≈P(0)+3P′(0)$

Responda

3.300

Mudanças no custo e na receita

Além de analisar o movimento ao longo de uma linha e o crescimento populacional, os derivativos são úteis para analisar mudanças no custo, receita e lucro. O conceito de função marginal é comum nas áreas de negócios e economia e implica o uso de derivativos. O custo marginal é a derivada da função de custo. A receita marginal é o derivado da função de receita. O lucro marginal é o derivado da função de lucro, que se baseia na função de custo e na função de receita.

Definição

• Se$C(x)$ for o custo de produção de$x$ itens, então o custo marginal$MC(x)$ é$MC(x)=C′(x)$.
• Se$R(x)$ for a receita obtida com a venda de$x$ itens, então a receita marginal$MR(x)$ é$MR(x)=R′(x)$.
• Se$P(x)=R(x)−C(x)$ for o lucro obtido com a venda de$x$ itens, então o lucro marginal$MP(x)$ é definido como sendo$MP(x)=P′(x)=MR(x)−MC(x)=R′(x)−C′(x)$.

Podemos aproximar aproximadamente

$$MC(x)=C′(x)=\lim_{h→0}\frac{C(x+h)−C(x)}{h} \nonumber$$

escolhendo um valor apropriado para$h$. Como$x$ representa objetos, um valor razoável e pequeno para$h$ é 1. Assim, ao substituir$h=1$, obtemos a aproximação$MC(x)=C′(x)≈C(x+1)−C(x)$. Consequentemente,$C′(x)$ para um determinado valor,$x$ pode-se pensar como a mudança no custo associada à produção de um item adicional. De forma semelhante,$MR(x)=R′(x)$ aproxima a receita obtida com a venda de um item adicional e$MP(x)=P′(x)$ se aproxima do lucro obtido pela produção e venda de um item adicional.

Exemplo$\PageIndex{6}$: Applying Marginal Revenue

Suponha que o número de jantares de churrasco que podem ser vendidos$x$,, possa estar relacionado ao preço cobrado$p$,, pela equação$p(x)=9−0.03x,0≤x≤300$.

Nesse caso, a receita em dólares obtida com a venda de jantares de$x$ churrasco é dada por

$R(x)=xp(x)=x(9−0.03x)=−0.03x^2+9x\;\text{ for }0≤x≤300$.

Use a função de receita marginal para estimar a receita obtida com a venda do jantar de$101^{\text{st}}$ churrasco. Compare isso com a receita real obtida com a venda deste jantar.

Solução

Primeiro, encontre a função de receita marginal:$MR(x)=R′(x)=−0.06x+9.$

Em seguida, use$R(101)−R(100)$,$R′(100)$ para aproximar, a receita obtida com a venda do$101^{\text{st}}$ jantar. Desde então$R′(100)=3$, a receita obtida com a venda do$101^{\text{st}}$ jantar é de aproximadamente $3.

A receita real obtida com a venda do$101^{\text{st}}$ jantar é

$R(101)−R(100)=602.97−600=2.97,$ou$$2.97.$

A receita marginal é uma estimativa bastante boa nesse caso e tem a vantagem de ser fácil de calcular.

Exercício$\PageIndex{4}$

Suponha que o lucro obtido com a venda de jantares$x$ de peixe frito seja dado por$P(x)=−0.03x^2+8x−50$. Use a função de lucro marginal para estimar o lucro da venda do jantar$101^{\text{st}}$ de peixe frito.

Dica

Use$P′(100)$ para aproximar$P(101)−P(100)$.

Responda

$2

Conceitos-chave

• Usando$f(a+h)≈f(a)+f′(a)h$, é possível estimar$f(a+h)$ dado$f′(a)$$f(a)$ e.
• A taxa de mudança de posição é velocidade e a taxa de mudança de velocidade é aceleração. Velocidade é o valor absoluto, ou magnitude, da velocidade.
• A taxa de crescimento populacional e a população atual podem ser usadas para prever o tamanho de uma população futura.
• As funções de custo marginal, receita marginal e lucro marginal podem ser usadas para prever, respectivamente, o custo de produção de mais um item, a receita obtida com a venda de mais um item e o lucro obtido pela produção e venda de mais um item.

Glossário

aceleração

é a taxa de variação da velocidade, ou seja, a derivada da velocidade

quantidade de alteração

a quantidade de uma função$f(x)$ em um intervalo$[x,x+h] is f(x+h)−f(x)$

taxa média de variação

é uma função$f(x)$ em um intervalo$[x,x+h]$ é$\frac{f(x+h)−f(a)}{b−a}$

custo marginal

é a derivada da função de custo, ou o custo aproximado de produzir mais um item

receita marginal

é o derivado da função de receita, ou a receita aproximada obtida com a venda de mais um item

lucro marginal

é o derivado da função de lucro, ou o lucro aproximado obtido pela produção e venda de mais um item

taxa de crescimento populacional

é a derivada da população em relação ao tempo

velocidade

é o valor absoluto da velocidade, ou seja,$|v(t)|$ é a velocidade de um objeto no momento$t$ cuja velocidade é dada por$v(t)$