3.2: A derivada como função
- Page ID
- 188520
- Defina a função derivada de uma determinada função.
- Faça um gráfico de uma função derivada do gráfico de uma determinada função.
- Declare a conexão entre derivadas e continuidade.
- Descreva três condições para quando uma função não tem uma derivada.
- Explique o significado de uma derivada de ordem superior.
Como vimos, a derivada de uma função em um determinado ponto nos dá a taxa de mudança ou inclinação da reta tangente à função naquele ponto. Se diferenciarmos uma função de posição em um determinado momento, obteremos a velocidade naquele momento. Parece razoável concluir que conhecer a derivada da função em cada ponto produziria informações valiosas sobre o comportamento da função. No entanto, o processo de encontrar a derivada até mesmo em alguns valores usando as técnicas da seção anterior rapidamente se tornaria bastante tedioso. Nesta seção, definimos a função derivada e aprendemos um processo para encontrá-la.
Funções derivadas
A função derivada fornece a derivada de uma função em cada ponto no domínio da função original para a qual a derivada é definida. Podemos definir formalmente uma função derivada da seguinte forma.
\(f\)Seja uma função. A função derivada, denotada por\(f'\), é a função cujo domínio consiste nos valores de\(x\) tal forma que existe o seguinte limite:
\[f'(x)=\lim_{h→0}\frac{f(x+h)−f(x)}{h}. \label{derdef} \]
\(f(x)\)Diz-se que uma função é diferenciável\(a\) se\(f'(a)\) existir. De forma mais geral, diz-se que uma função é diferenciável\(S\) se for diferenciável em cada ponto de um conjunto aberto\(S\), e uma função diferenciável é aquela em que\(f'(x)\) existe em seu domínio.
Nos próximos exemplos, usamos a Equação\ ref {derdef} para encontrar a derivada de uma função.
Encontre a derivada de\(f(x)=\sqrt{x}\).
Solução
Comece diretamente com a definição da função derivada.
Substitua\(f(x+h)=\sqrt{x+h}\) e\(f(x)=\sqrt{x}\) entre\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\).
| \(f'(x)=\displaystyle \lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}⋅\frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}\) | Multiplique o numerador e o denominador por\(\sqrt{x+h}+\sqrt{x}\) sem distribuir no denominador. |
| \(=\displaystyle\lim_{h→0}\frac{h}{h\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Multiplique os numeradores e simplifique. |
| \(=\displaystyle\lim_{h→0}\frac{1}{\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Cancele\(h\) o. |
| \(=\dfrac{1}{2\sqrt{x}}\) | Avalie o limite |
Encontre a derivada da função\(f(x)=x^2−2x\).
Solução
Siga o mesmo procedimento aqui, mas sem precisar multiplicar pelo conjugado.
Substituir\(f(x+h)=(x+h)^2−2(x+h)\) e\(f(x)=x^2−2x\) entrar\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle\lim_{h→0}\frac{((x+h)^2−2(x+h))−(x^2−2x)}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{x^2+2xh+h^2−2x−2h−x^2+2x}{h}\) | Expandir\((x+h)^2−2(x+h)\). |
| \(=\displaystyle\lim_{h→0}\frac{2xh−2h+h^2}{h}\) | Simplifique |
| \(=\displaystyle\lim_{h→0}\frac{h(2x−2+h)}{h}\) | Fator a\(h\) partir do numerador |
| \(=\displaystyle\lim_{h→0}(2x−2+h)\) | Cancele o fator comum de\(h\) |
| \(=2x−2\) | Avalie o limite |
Encontre a derivada de\(f(x)=x^2\).
- Dica
-
Use a Equação\ ref {derdef} e siga o exemplo.
- Responda
-
\(f'(x)=2x\)
Usamos uma variedade de notações diferentes para expressar a derivada de uma função. No exemplo,\(\PageIndex{2}\) mostramos que se\(f(x)=x^2−2x\), então\(f'(x)=2x−2\). Se tivéssemos expressado essa função na forma\(y=x^2−2x\), poderíamos ter expressado a derivada como\(y′=2x−2\) ou\(\dfrac{dy}{dx}=2x−2\). Poderíamos ter transmitido a mesma informação por escrito\(\dfrac{d}{dx}\left(x^2−2x\right)=2x−2\). Assim, para a função\(y=f(x)\), cada uma das seguintes notações representa a derivada de\(f(x)\):
\(f'(x), \quad \dfrac{dy}{dx}, \quad y′,\quad \dfrac{d}{dx}\big(f(x)\big)\).
No lugar de\(f'(a)\), também podemos usar\(\dfrac{dy}{dx}\Big|_{x=a}\). O uso da\(\dfrac{dy}{dx}\) notação (chamada de notação de Leibniz) é bastante comum em engenharia e física. Para entender melhor essa notação, lembre-se de que a derivada de uma função em um ponto é o limite das inclinações das retas secantes à medida que as linhas secantes se aproximam da reta tangente. As inclinações dessas linhas secantes são frequentemente expressas na forma em\(\dfrac{Δy}{Δx}\) que\(Δy\) está a diferença nos\(y\) valores correspondentes à diferença nos\(x\) valores, que são expressos como\(Δx\) (Figura\(\PageIndex{1}\)). Assim, a derivada, que pode ser considerada como a taxa instantânea de variação de em\(y\) relação a\(x\), é expressa como
\(\displaystyle \frac{dy}{dx}= \lim_{Δx→0}\frac{Δy}{Δx}\).
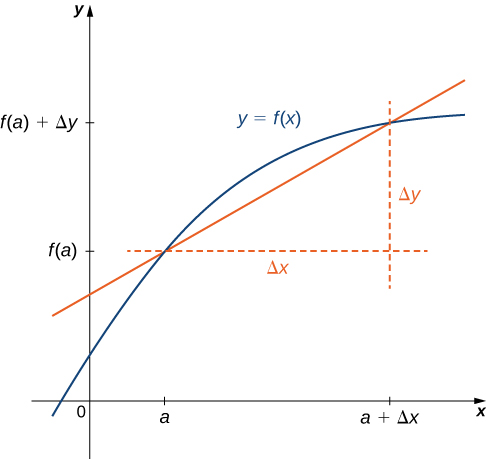
Representação gráfica de uma derivada
Já discutimos como representar graficamente uma função, então, dada a equação de uma função ou a equação de uma função derivada, poderíamos representá-la graficamente. Considerando ambas, esperaríamos ver uma correspondência entre os gráficos dessas duas funções, uma vez que\(f'(x)\) fornece a taxa de mudança de uma função\(f(x)\) (ou inclinação da reta tangente a\(f(x)\)).
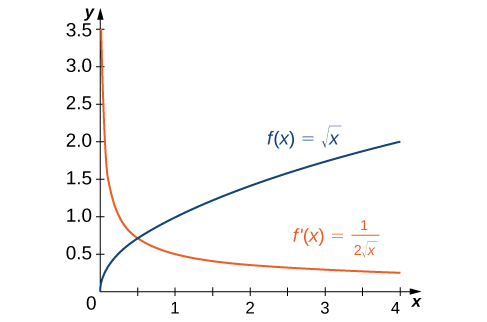
No exemplo\(\PageIndex{1}\),, descobrimos que para\(f(x)=\sqrt{x}\),\(f'(x)=\frac{1}{2\sqrt{x}}\). Se representarmos graficamente essas funções nos mesmos eixos\(\PageIndex{2}\), como na Figura, podemos usar os gráficos para entender a relação entre essas duas funções. Primeiro, notamos que\(f(x)\) está aumentando em todo o seu domínio, o que significa que as inclinações de suas retas tangentes em todos os pontos são positivas. Consequentemente, esperamos todos\(f'(x)>0\) os valores de x em seu domínio. Além disso, à medida que\(x\) aumenta, as inclinações das retas tangentes\(f(x)\) estão diminuindo e esperamos ver uma diminuição correspondente em\(f'(x)\). Também observamos que\(f(0)\) é indefinido e que\(\displaystyle \lim_{x→0^+}f'(x)=+∞\), correspondendo a uma tangente vertical a\(f(x)\) at\(0\).
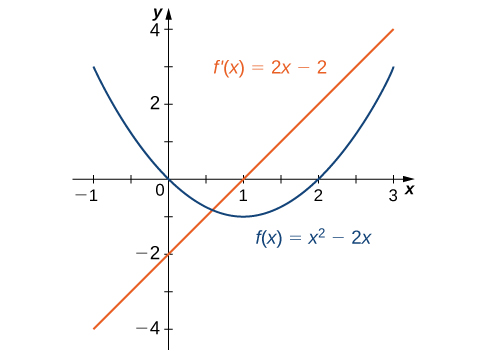
Em exemplo\(\PageIndex{2}\), descobrimos isso para\(f(x)=x^2−2x,\; f'(x)=2x−2\). Os gráficos dessas funções são mostrados na Figura\(\PageIndex{3}\). Observe que\(f(x)\) está diminuindo para\(x<1\). Para esses mesmos valores de\(x\),\(f'(x)<0\). Para valores de\(x>1\),\(f(x)\) está aumentando\(f'(x)>0\) e. Além disso,\(f(x)\) tem uma tangente horizontal em\(x=1\)\(f'(1)=0\) e.
Use o gráfico a seguir de\(f(x)\) para esboçar um gráfico de\(f'(x)\).
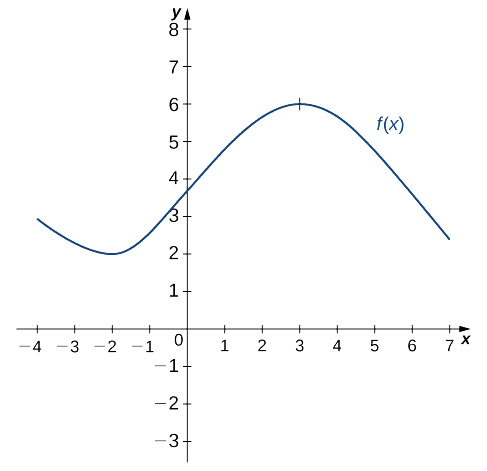
Solução
A solução é mostrada no gráfico a seguir. Observe que\(f(x)\) está aumentando e assim\(f'(x)>0\) por diante\((–2,3)\). Além disso,\(f(x)\) está diminuindo\((−∞,−2)\) e\(f'(x)<0\) assim por diante\((3,+∞)\). Observe também que\(f(x)\) tem tangentes horizontais em\(–2\) e\(3\),\(f'(−2)=0\) e\(f'(3)=0\) e.
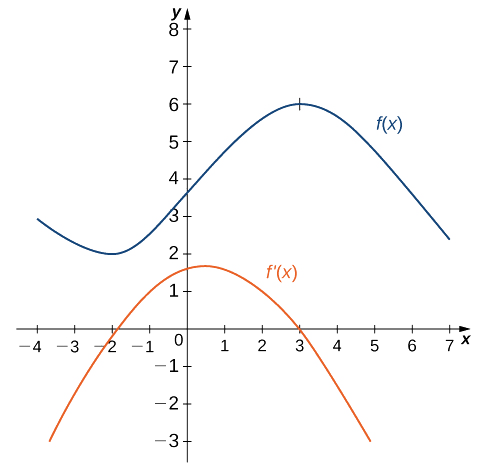
Esboce o gráfico de\(f(x)=x^2−4\). Em que intervalo está o gráfico\(f'(x)\) acima do\(x\) eixo -?
- Dica
-
O gráfico de\(f'(x)\) é positivo onde\(f(x)\) está aumentando.
- Responda
-
\((0,+∞)\)
Derivadas e continuidade
Agora que podemos representar graficamente uma derivada, vamos examinar o comportamento dos gráficos. Primeiro, consideramos a relação entre diferenciabilidade e continuidade. Veremos que se uma função é diferenciável em um ponto, ela deve ser contínua lá; no entanto, uma função que é contínua em um ponto não precisa ser diferenciável nesse ponto. Na verdade, uma função pode ser contínua em um ponto e não ser diferenciável no ponto por uma das várias razões.
\(f(x)\)Seja uma função e\(a\) esteja em seu domínio. Se\(f(x)\) é diferenciável em\(a\), então\(f\) é contínuo em\(a\).
Se\(f(x)\) é diferenciável em\(a\), então\(f'(a)\) existe e, se deixarmos\(h = x - a\), temos\( x = a + h \), e como\(h=x-a\to 0\), podemos ver isso\(x\to a\).
Então
\[ f'(a) = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\nonumber \]
pode ser reescrito como
\(f'(a)=\displaystyle \lim_{x→a}\frac{f(x)−f(a)}{x−a}\).
Queremos mostrar que\(f(x)\) é uma arte contínua,\(a\) mostrando que\(\displaystyle \lim_{x→a}f(x)=f(a).\) Assim,
\ (\ begin {align*}\ estilo de exibição\ lim_ {x→a} f (x) &=\ lim_ {x→a}\;\ big (f (x) −f (a) +f (a)\ grande)\ [4pt]
&=\ lim_ {x→a}\ left (\ frac {f (x) −f (a)} {x−a}. (x−a) +f (a)\ right) & &\ text {Multiplique e divida} (f (x) −f (a))\ text {por} x−a.\\ [4pt]
&=\ left (\ lim_ {x→a}\ frac {f (x) −f (a)} {x−a}\ direita) ‣\ esquerda (\ lim_ {x→a}\; (x−a)\ direita) +\ lim_ {x→a} f (a)\\ [4pt]
&=f' (a) ⋅0+f (a)\\ [4pt]
&=f (a). \ end {align*}\)
Portanto, uma vez que\(f(a)\) é definido e\(\displaystyle \lim_{x→a}f(x)=f(a)\), concluímos que\(f\) é contínuo em\(a\).
□
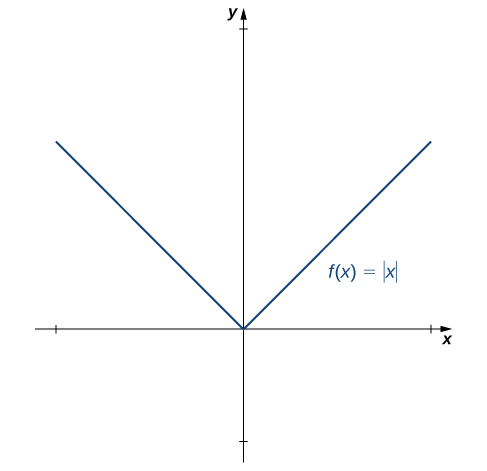
Acabamos de provar que diferenciabilidade implica continuidade, mas agora consideramos se continuidade implica diferenciabilidade. Para determinar uma resposta a essa pergunta, examinamos a função\(f(x)=|x|\). Essa função é contínua em todos os lugares; no entanto,\(f'(0)\) é indefinida. Essa observação nos leva a acreditar que continuidade não implica diferenciabilidade. Vamos explorar mais. Para\(f(x)=|x|\),
\(f'(0)=\displaystyle \lim_{x→0}\frac{f(x)−f(0)}{x−0}= \lim_{x→0}\frac{|x|−|0|}{x−0}= \lim_{x→0}\frac{|x|}{x}\).
Esse limite não existe porque
\(\displaystyle \lim_{x→0^−}\frac{|x|}{x}=−1\)\(\displaystyle \lim_{x→0^+}\frac{|x|}{x}=1\)e.
Veja a Figura\(\PageIndex{4}\).
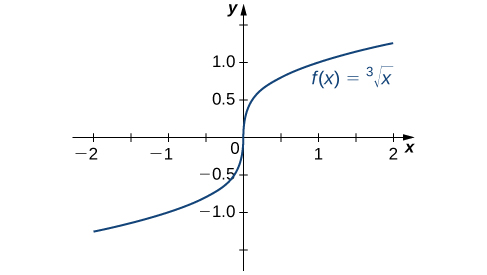
Vamos considerar algumas situações adicionais nas quais uma função contínua não é diferenciável. Considere a função\(f(x)=\sqrt[3]{x}\):
\(f'(0)=\displaystyle \lim_{x→0}\frac{\sqrt[3]{x}−0}{x−0}=\displaystyle \lim_{x→0}\frac{1}{\sqrt[3]{x^2}}=+∞\).
Portanto,\(f'(0)\) não existe. Uma rápida olhada no gráfico de\(f(x)=\sqrt[3]{x}\) esclarece a situação. A função tem uma linha tangente vertical em\(0\) (Figura\(\PageIndex{5}\)).
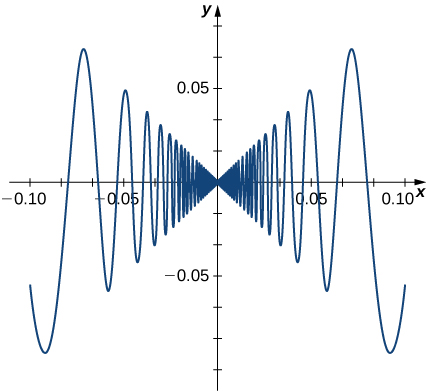
A função\(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & & \text{ if } x=0\end{cases}\) também tem uma derivada que exibe um comportamento interessante em\(0\).
Nós vemos isso
\(f'(0)=\displaystyle \lim_{x→0}\frac{x\sin\left(1/x\right)−0}{x−0}= \lim_{x→0}\sin\left(\frac{1}{x}\right)\).
Esse limite não existe, essencialmente porque as inclinações das linhas secantes mudam continuamente de direção à medida que se aproximam de zero (Figura\(\PageIndex{6}\)).
Em resumo:
- Observamos que se uma função não é contínua, ela não pode ser diferenciável, pois toda função diferenciável deve ser contínua. No entanto, se uma função for contínua, ela ainda pode não ser diferenciável.
- Vimos que isso\(f(x)=|x|\) não era diferenciável\(0\) porque o limite das inclinações das retas tangentes à esquerda e à direita não era o mesmo. Visualmente, isso resultou em um canto nítido no gráfico da função em. A\(0.\) partir disso, concluímos que, para ser diferenciável em um ponto, uma função deve ser “suave” nesse ponto.
- Como vimos no exemplo de\(f(x)=\sqrt[3]{x}\), uma função falha em ser diferenciável em um ponto onde há uma reta tangente vertical.
- Como vimos,\(f(x)=\begin{cases}x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & &\text{ if } x=0\end{cases}\) uma função também pode não ser diferenciável em um ponto de maneiras mais complicadas.
Uma empresa de brinquedos quer projetar uma pista para um carro de brinquedo que começa ao longo de uma curva parabólica e depois se converte em uma linha reta (Figura\(\PageIndex{7}\)). A função que descreve a trilha é ter a forma\(f(x)=\begin{cases}\frac{1}{10}x^2+bx+c, & & \text{ if }x<−10\\−\frac{1}{4}x+\frac{5}{2}, & & \text{ if } x≥−10\end{cases}\) onde\(x\) e\(f(x)\) estão em polegadas. Para que o carro se mova suavemente ao longo da pista, a função\(f(x)\) deve ser contínua e diferenciável em\(−10\). Encontre valores de\(b\) e\(c\) que\(f(x)\) os tornam contínuos e diferenciáveis.
Solução
Para que a função seja contínua em\(x=−10\),\(\displaystyle \lim_{x→10^−}f(x)=f(−10)\). Assim, uma vez que
\(\displaystyle \lim_{x→−10^−}f(x)=\frac{1}{10}(−10)^2−10b+c=10−10b+c\)
e\(f(−10)=5\), devemos ter\(10−10b+c=5\). Equivalentemente, nós temos\(c=10b−5\).
Para que a função seja diferenciável em\(−10\),
\(f'(10)=\displaystyle \lim_{x→−10}\frac{f(x)−f(−10)}{x+10}\)
deve existir. Como\(f(x)\) é definido usando regras diferentes à direita e à esquerda, devemos avaliar esse limite da direita e da esquerda e, em seguida, defini-los iguais entre si:
\ (\ estilo de exibição\ begin {align*}\ lim_ {x→−10^−}\ frac {f (x) −f (−10)} {x+10} &=\ lim_ {x→−10^−}\ frac {\ frac {1} {10} x^2+bx+c−5} {x+10}\\ [4pt]
&=\ lim_ {x→−10^−}\ frac {\ frac {1} {10} x^2+bx+ (10b−5) −5} {x+10} & &\ texto {Substituto} c=10b−5.\\ [4pt]
&=\ lim_ {x→−10^−}\ frac {x^2−100+10bx+ 100b} {10 (x+10)}\\ [4pt]
&=\ lim_ {x→−10^−}\ frac {(x+10) (x−10+10b)} {10 (x+10)} & &\ text {Fator por agrupamento}\\ [4pt]
&=b−2\ end {align*}\).
Nós também temos
\ (\ estilo de exibição\ begin {align*}\ lim_ {x→−10^+}\ frac {f (x) −f (−10)} {x+10} &=\ lim_ {x→−10^+}\ frac {−\ frac {1} {4} x+\ frac {5} {2} −5} {x+10}\\ [4pt]
&=\ lim_ {x→−10^+}\ frac {− (x+10)} {4 (x+10)}\\ [4pt]
&=−\ frac {1} {4}\ end {align*}\).
Isso nos dá\(b−2=−\frac{1}{4}\). Assim\(b=\frac{7}{4}\),\(c=10(\frac{7}{4})−5=\frac{25}{2}\) e.
Encontre valores de a e b que tornam\(f(x)=\begin{cases}ax+b, & & \text{ if } x<3\\x^2, & & \text{ if } x≥3\end{cases}\) ambos contínuos e diferenciáveis em\(3\).
- Dica
-
Use o exemplo\(\PageIndex{4}\) como guia.
- Responda
-
\(a=6\)e\(b=−9\)
Derivados de ordem superior
A derivada de uma função é em si uma função, então podemos encontrar a derivada de uma derivada. Por exemplo, a derivada de uma função de posição é a taxa de mudança de posição ou velocidade. A derivada da velocidade é a taxa de variação da velocidade, que é a aceleração. A nova função obtida pela diferenciação da derivada é chamada de segunda derivada. Além disso, podemos continuar usando derivadas para obter a terceira derivada, a quarta derivada e assim por diante. Coletivamente, eles são chamados de derivativos de ordem superior. A notação para as derivadas de ordem superior de\(y=f(x)\) pode ser expressa em qualquer uma das seguintes formas:
\(f''(x),\; f'''(x),\; f^{(4)}(x),\; …\; ,\; f^{(n)}(x)\)
\(y''(x),\; y'''(x),\; y^{(4)}(x),\; …\; ,\; y^{(n)}(x)\)
\(\dfrac{d^2y}{dx^2},\;\dfrac{d^3y}{dy^3},\;\dfrac{d^4y}{dy^4},\;…\;,\;\dfrac{d^ny}{dy^n}.\)
É interessante notar que a notação para\(\dfrac{d^2y}{dx^2}\) pode ser vista como uma tentativa de se expressar de forma\(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\) mais compacta.
Analogamente,\(\dfrac{d}{dx}\left(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\right)=\dfrac{d}{dx}\left(\dfrac{d^2y}{dx^2}\right)=\dfrac{d^3y}{dx^3}\).
Para\(f(x)=2x^2−3x+1\), encontre\(f''(x)\).
Solução
Primeira descoberta\(f'(x)\).
Substituir\(f(x)=2x^2−3x+1\) e\(f(x+h)=2(x+h)^2−3(x+h)+1\) entrar\(f'(x)=\displaystyle \lim_{h→0}\dfrac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle \lim_{h→0}\frac{(2(x+h)^2−3(x+h)+1)−(2x^2−3x+1)}{h}\) | |
| \(=\displaystyle \lim_{h→0}\frac{4xh+2h^2−3h}{h}\) | Simplifique o numerador. |
| \(=\displaystyle \lim_{h→0}(4x+2h−3)\) | Fatize o\(h\) no numerador e cancele com o\(h\) no denominador. |
| \(=4x−3\) | Pegue o limite. |
Em seguida, encontre\(f''(x)\) usando a derivada de\(f'(x)=4x−3.\)
| \(f''(x)=\displaystyle \lim_{h→0}\frac{f'(x+h)−f'(x)}{h}\) | Use\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\) com\(f ′(x)\) no lugar de\(f(x).\) |
| \(=\displaystyle \lim_{h→0}\frac{(4(x+h)−3)−(4x−3)}{h}\) | Substituir\(f'(x+h)=4(x+h)−3\) e\(f'(x)=4x−3.\) |
| \(=\displaystyle \lim_{h→0}4\) | Simplifique. |
| \(=4\) | Pegue o limite. |
Encontre\(f''(x)\) por\(f(x)=x^2\).
- Dica
-
Encontramos\(f'(x)=2x\) em um posto de controle anterior. Use a Equação\ ref {derdef} para encontrar a derivada de\(f'(x)\)
- Responda
-
\(f''(x)=2\)
A posição de uma partícula ao longo de um eixo de coordenadas no tempo\(t\) (em segundos) é dada por\(s(t)=3t^2−4t+1\) (em metros). Encontre a função que descreve sua aceleração no momento\(t\).
Solução
Desde\(v(t)=s′(t)\) e\(a(t)=v′(t)=s''(t)\), começamos encontrando a derivada de\(s(t)\):
\ (\ estilo de exibição\ begin {align*} s′( t) &=\ lim_ {h→0}\ frac {s (t+h) −s (t)} {h}\\ [4pt]
&=\ lim_ {h→0}\ frac {3 (t+h) ^2−4 (t+h) +1− (3t^2−4t+1} {h}\\ [4pt]
&=6t−4. \ end {align*}\)
Em seguida,
\ (\ displaystyle\ begin {align*} s “(t) &=\ lim_ {h→0}\ frac {s′( t+h) −s′s (t)} {h}\\ [4pt]
&=\ lim_ {h→0}\ frac {6 (t+h) −4− (6t−4)} {h}\\ [4pt]
6. \ end {align*}\)
Assim,\(a=6 \;\text{m/s}^2\).
Para\(s(t)=t^3\), encontre\(a(t).\)
- Dica
-
Use o exemplo\(\PageIndex{6}\) como guia.
- Responda
-
\(a(t)=6t\)
Conceitos-chave
- A derivada de uma função\(f(x)\) é a função cujo valor em\(x\) é\(f'(x)\).
- O gráfico de uma derivada de uma função\(f(x)\) está relacionado ao gráfico de\(f(x)\). Onde\(f(x)\) tem uma reta tangente com inclinação positiva,\(f'(x)>0\). Onde\(f(x)\) tem uma reta tangente com inclinação negativa,\(f'(x)<0\). Onde\(f(x)\) tem uma linha tangente horizontal,\(f'(x)=0.\)
- Se uma função é diferenciável em um ponto, ela é contínua nesse ponto. Uma função não é diferenciável em um ponto se não for contínua no ponto, se tiver uma linha tangente vertical no ponto ou se o gráfico tiver um canto ou cúspide nítido.
- Derivadas de ordem superior são derivadas de derivadas, da segunda derivada para a\(n^{\text{th}}\) derivada.
Equações-chave
- A função derivada
\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\)
Glossário
- função derivada
- fornece a derivada de uma função em cada ponto no domínio da função original para a qual a derivada é definida
- diferenciável em\(a\)
- uma função para a qual\(f'(a)\) existe é diferenciável em\(a\)
- diferenciável em\(S\)
- uma função que\(f'(x)\) existe para cada uma\(x\) no conjunto aberto\(S\) é diferenciável em\(S\)
- função diferenciável
- uma função para a qual\(f'(x)\) existe é uma função diferenciável
- derivada de ordem superior
- uma derivada de uma derivada, da segunda derivada para a\(n^{\text{th}}\) derivada, é chamada de derivada de ordem superior
Contribuidores e atribuições
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) added explanation of the alternative definition of the derivative used in the proof of that differentiability implies continuity.


