3.1E: Exercícios para a Seção 3.1

Last updated
Save as PDF

Page ID: 188507

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para os exercícios 1 a 10, use a equação$ m_{\text{sec}}=\dfrac{f(x)−f(a)}{x−a} $ para encontrar a inclinação da linha secante entre os valores$x_1$ e$x_2$ para cada função$y=f(x)$.

1)$f(x)=4x+7; \quad x_1=2, \quad x_2=5$

Resposta: $m_{\text{sec}}=4$

2)$f(x)=8x−3;\quad x_1=−1,\quad x_2=3$

3)$f(x)=x^2+2x+1;\quad x_1=3,\quad x_2=3.5$

Resposta: $m_{\text{sec}}=8.5$

4)$f(x)=−x^2+x+2;\quad x_1=0.5,\quad x_2=1.5$

5)$f(x)=\dfrac{4}{3x−1};\quad x_1=1,\quad x_2=3$

Resposta: $m_{\text{sec}}=−\frac{3}{4}$

6)$f(x)=\dfrac{x−7}{2x+1};\quad x_1=−2,\quad x_2=0$

7)$f(x)=\sqrt{x};\quad x_1=1,\quad x_2=16$

Resposta: $m_{\text{sec}}=0.2$

8)$f(x)=\sqrt{x−9};\quad x_1=10,\quad x_2=13$

9)$f(x)=x^{1/3}+1;\quad x_1=0,\quad x_2=8$

Resposta: $m_{\text{sec}}=0.25$

10)$f(x)=6x^{2/3}+2x^{1/3};\quad x_1=1,\quad x_2=27$

Para as funções dos exercícios 11 a 20,

a. use a equação$ \displaystyle m_{\text{tan}}=\lim_{h→0}\frac{f(a+h)−f(a)}{h} $ para encontrar a inclinação da reta$m_{\text{tan}}=f′(a)$ tangente e

b. encontre a equação da reta tangente a$f$ at$x=a$.

11)$f(x)=3−4x, \quad a=2$

Resposta: a.$m_{\text{tan}}=−4$
b.$y=−4x+3$

12)$f(x)=\dfrac{x}{5}+6, \quad a=−1$

13)$f(x)=x^2+x, \quad a=1$

Resposta: a.$m_{\text{tan}}=3$
b.$y=3x−1$

14)$f(x)=1−x−x^2, \quad a=0$

15)$f(x)=\dfrac{7}{x}, \quad a=3$

Resposta: a.$m_{\text{tan}}=\frac{−7}{9}$
b.$y=\frac{−7}{9}x+\frac{14}{3}$

16)$f(x)=\sqrt{x+8}, \quad a=1$

17)$f(x)=2−3x^2, \quad a=−2$

Resposta: a.$m_{\text{tan}}=12$
b.$y=12x+14$

18)$f(x)=\dfrac{−3}{x−1}, \quad a=4$

19)$f(x)=\dfrac{2}{x+3}, \quad a=−4$

Resposta: a.$m_{\text{tan}}=−2$
b.$y=−2x−10$

20)$f(x)=\dfrac{3}{x^2}, \quad a=3$

Para as funções$y=f(x)$ nos exercícios 21 a 30, encontre$f′(a)$ usando a equação$ \displaystyle f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a} $.

21)$f(x)=5x+4, \quad a=−1$

Resposta: $f'(-1) = 5$

22)$f(x)=−7x+1, \quad a=3$

23)$f(x)=x^2+9x, \quad a=2$

Resposta: $f'(2) = 13$

24)$f(x)=3x^2−x+2, \quad a=1$

25)$f(x)=\sqrt{x}, \quad a=4$

Resposta: $f'(4) = \frac{1}{4}$

26)$f(x)=\sqrt{x−2}, \quad a=6$

27)$f(x)=\dfrac{1}{x}, \quad a=2$

Resposta: $f'(2) = −\frac{1}{4}$

28)$f(x)=\dfrac{1}{x−3}, \quad a=−1$

29)$f(x)=\dfrac{1}{x^3}, \quad a=1$

Resposta: $f'(1) = -3$

30)$f(x)=\dfrac{1}{\sqrt{x}}, \quad a=4$

Para os exercícios a seguir, dada a função$y=f(x)$,

a. encontre a inclinação da linha secante$PQ$ para cada ponto$Q(x,f(x))$ com o$x$ valor dado na tabela.

b. Use as respostas de a. para estimar o valor da inclinação da reta tangente em$P$.

c. Use a resposta de b. para encontrar a equação da reta tangente até o$f$ ponto$P$.

31) [T]$f(x)=x^2+3x+4, \quad P(1,8)$ (Arredondar para$6$ casas decimais.)

$x$	$Slope m_{PQ}$	$x$	$Slope m_{PQ}$
1.1	(i)	0,9	(vii)
1,01	(ii)	0,99	(viii)
1.001	(iii)	0,999	(ix)
1.0001	(iv)	0,999	(x)
1.00001	(v)	0,9999	(xi)
1.000001	(vi)	0,999999	(xii)

Resposta: $a. (i)5.100000, (ii)5.010000, (iii)5.001000, (iv)5.000100, (v)5.000010, (vi)5.000001, (vii)4.900000, (viii)4.990000, (ix)4.999000, (x)4.999900, (xi)4.999990, (x)4.999999$
b.$m_{\text{tan}}=5$
c.$y=5x+3$

32) [T]$f(x)=\dfrac{x+1}{x^2−1}, \quad P(0,−1)$

$x$	$Slope m_{PQ}$	$x$	$Slope m_{PQ}$
0.1	(i)	−0,1	(vii)
0,01	(ii)	−0,01	(viii)
0,001	(iii)	−0,001	(ix)
0,0001	(iv)	−0,0001	(x)
0,00001	(v)	−0,00001	(xi)
0,000001	(vi)	−0,000001	(xii)

33) [T]$f(x)=10e^{0.5x}, \quad P(0,10)$ (Arredondar para$4$ casas decimais.)

$x$	$Slope m_{PQ}$
−0,1	(i)
−0,01	(ii)
−0,001	(iii)
−0,0001	(iv)
−0,00001	(v)
−0,000001	(vi)

Resposta: a.$(i)4.8771, \;(ii)4.9875, \;(iii)4.9988, \;(iv)4.9999, \;(v)4.9999, \;(vi)4.9999 $
b.$m_{\text{tan}}=5$
c.$y=5x+10$

34) [T]$f(x)=\tan(x), \quad P(π,0)$

$x$	$Slope m_{PQ}$
3.1	(i)
3,14	(ii)
3.141	(iii)
3.1415	(iv)
3.14159	(v)
3.141592	(vi)

[T] Para as seguintes funções de posição$y=s(t)$, um objeto está se movendo ao longo de uma linha reta, onde$t$ está em segundos e$s$ está em metros. Encontre

a. a expressão simplificada para a velocidade média de$t=2$ até$t=2+h$;

b. a velocidade média entre$t=2$ e$t=2+h$, onde$(i)\;h=0.1, \;(ii)\;h=0.01, \;(iii)\;h=0.001$, e$(iv)\;h=0.0001$; e

c. use a resposta de a. para estimar a velocidade instantânea em$t=2$ segundos.

35)$s(t)=\frac{1}{3}t+5$

Resposta: a.$\frac{1}{3}$;
b.$(i)\;\frac{1}{3}$ m/s,$(ii)\;\frac{1}{3}$ m/s,$(iii)\;\frac{1}{3}$ m/s,$(iv)\;\frac{1}{3}$ m/s;
c.$\frac{1}{3}$ m/s

36)$s(t)=t^2−2t$

37)$s(t)=2t^3+3$

Resposta: a.$2(h^2+6h+12)$;
b.$(i)\;25.22$ m/s,$(ii)\; 24.12$ m/s,$(iii)\; 24.01$ m/s,$(iv)\; 24$ m/s;
c.$24$ m/s

38)$s(t)=\dfrac{16}{t^2}−\dfrac{4}{t}$

39) Use o gráfico a seguir para avaliar a.$f′(1)$ e b.$f′(6).$

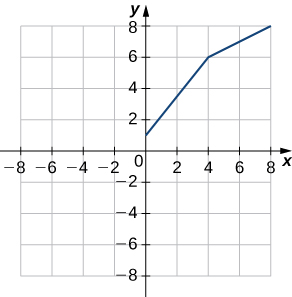
$Este gráfico mostra dois segmentos de linha conectados: um indo de (1, 0) para (4, 6) e o outro indo de (4, 6) para (8, 8).$

Resposta: a.$1.25$; b.$0.5$

40) Use o gráfico a seguir para avaliar a.$f′(−3)$ e b.$f′(1.5)$

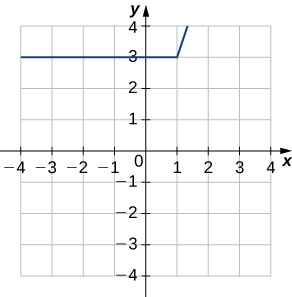
$Este gráfico mostra dois segmentos de linha conectados: um indo de (−4, 3) para (1, 3) e o outro indo de (1, 3) para (1,5, 4).$

Para os exercícios a seguir, use a definição limite de derivada para mostrar que a derivada não existe em$x=a$ para cada uma das funções dadas.

41)$f(x)=x^{1/3}, \quad x=0$

Resposta: $\displaystyle \lim_{x→0^−}\frac{x^{1/3}−0}{x−0}=\lim_{x→0^−}\frac{1}{x^{2/3}}=∞$

42)$f(x)=x^{2/3}, \quad x=0$

43)$f(x)=\begin{cases}1, & \text{if } x<1\\x, & \text{if } x≥1\end{cases}, \quad x=1$

Resposta: $\displaystyle \lim_{x→1^−}\frac{1−1}{x−1}=0≠1=\lim_{x→1^+}\frac{x−1}{x−1}$

44)$f(x)=\dfrac{|x|}{x}, \quad x=0$

45) [T] A posição em pés de um carro de corrida ao longo de uma pista reta após$t$ segundos é modelada pela função$s(t)=8t^2−\frac{1}{16}t^3.$

a. Encontre a velocidade média do veículo nos seguintes intervalos de tempo até quatro casas decimais:

Eu. [...$4, 4.1$]

ii. [$4, 4.01$]

iii. [$4, 4.001$]

iv. [$4, 4.0001$]

b. Use a. para tirar uma conclusão sobre a velocidade instantânea do veículo em$t=4$ segundos.

Resposta: a.$(i)61.7244 ft/s, \;(ii)61.0725 ft/s, \;(iii)61.0072 ft/s, \;(iv)61.0007 ft/s$
b. Em$4$ segundos, o carro de corrida está viajando a uma taxa/velocidade de$61$ pés/s.

46) [T] A distância em pés que uma bola rola por uma inclinação é modelada pela função$s(t)=14t^2$,

onde t é segundos depois que a bola começa a rolar.

a. Encontre a velocidade média da bola nos seguintes intervalos de tempo:

i. [5, 5.1]

ii. [5, 5,01]

iii. [5, 5.001]

iv. [5, 5.0001]

b. Use as respostas de a. para tirar uma conclusão sobre a velocidade instantânea da bola em$t=5$ segundos.

47) Dois veículos começam viajando lado a lado por uma estrada reta. Suas funções de posição, mostradas no gráfico a seguir, são dadas por$s=f(t)$ e$s=g(t)$, onde s é medido em pés e t é medido em segundos.

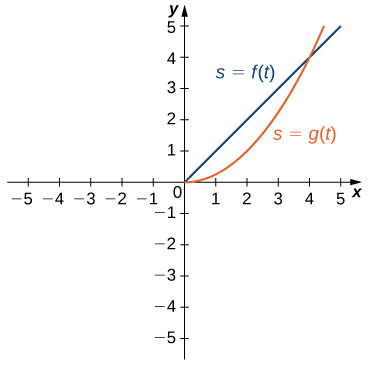
$Duas funções s = g (t) e s = f (t) são representadas graficamente. A primeira função s = g (t) começa em (0, 0) e se curva para cima, passando por aproximadamente (2, 1) até (4, 4). A segunda função s = f (t) é uma linha reta passando por (0, 0) e (4, 4).$

a. Qual veículo viajou mais longe em$t=2$ segundos?

b. Qual é a velocidade aproximada de cada veículo em$t=3$ segundos?

c. Qual veículo está viajando mais rápido em$t=4$ segundos?

d. O que é verdade sobre as posições dos veículos em$t=4$ segundos?

Resposta: a. O veículo representado por$f(t)$, porque percorreu$2$ pés, enquanto$g(t)$ percorreu a$1$ pé.
b. A velocidade de$f(t)$ é constante em$1$ pés/s, enquanto a velocidade de$g(t)$ é de aproximadamente$2$ pés/s.
c. O veículo representado por$g(t)$, com uma velocidade de aproximadamente$4$ pés/s.
d. Ambos viajaram $4$pés em$4$ segundos.

48) [T] O custo total$C(x)$, em centenas de dólares, para produzir$x$ potes de maionese é dado por$C(x)=0.000003x^3+4x+300$.

a. Calcule o custo médio por jarra nos seguintes intervalos:

i. [100, 100,1]

ii. [100, 100,01]

iii. [100, 100,001]

iv. [100, 100,0001]

b. Use as respostas de a. para estimar o custo médio de produção de$100$ frascos de maionese.

49) [T] Para a função$f(x)=x^3−2x^2−11x+12$, faça o seguinte.

a. Use uma calculadora gráfica para representar graficamente$f$ em uma janela de visualização apropriada.

b. Use o recurso ZOOM na calculadora para aproximar os dois valores dos$x=a$ quais$m_{tan}=f′(a)=0$.

Resposta

uma.

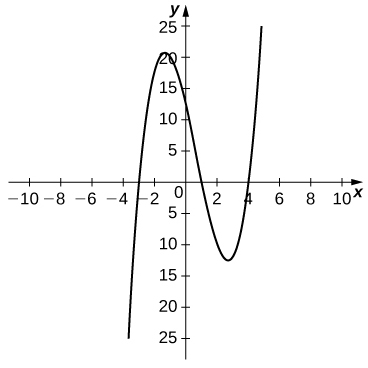
$A função começa no terceiro quadrante, passa pelo eixo x em x = −3, aumenta até um máximo em torno de y = 20, diminui e passa pelo eixo x em x = 1, continua diminuindo ao mínimo em torno de y = −13 e depois aumenta através do eixo x em x = 4, após o qual continua aumentando.$

b.$a≈−1.361,\;2.694$

50) [T] Para a função$f(x)=\dfrac{x}{1+x^2}$, faça o seguinte.

a. Use uma calculadora gráfica para representar graficamente$f$ em uma janela de visualização apropriada.

b. Use o recurso ZOOM na calculadora para aproximar os valores dos$x=a$ quais$m_{\text{tan}}=f′(a)=0$.

51) Suponha que$N(x)$ calcule o número de galões de gás usados por um veículo viajando$x$ milhas. Suponha que o veículo receba$30$ mpg.

a. Encontre uma expressão matemática para$N(x)$.

b. O que é$N(100)$? Explique o significado físico.

c. O que é$N′(100)$? Explique o significado físico.

Resposta: a.$N(x)=\dfrac{x}{30}$
b. ≠$3.3$ galões. Quando o veículo viaja$100$ quilômetros, ele usa$3.3$ galões de gasolina.
$\frac{1}{30}$c. A taxa de consumo de gás em galões por milha que o veículo está atingindo depois de ter percorrido$100$ milhas.

52) [T] Para a função$f(x)=x^4−5x^2+4$, faça o seguinte.

a. Use uma calculadora gráfica para representar graficamente$f$ em uma janela de visualização apropriada.

b. Use a$nDeriv$ função, que encontra numericamente a derivada, em uma calculadora gráfica para estimar$f′(−2),\;f′(−0.5),\;f′(1.7)$,$f′(2.718)$ e.

53) [T] Para a função$f(x)=\dfrac{x^2}{x^2+1}$, faça o seguinte.

a. Use uma calculadora gráfica para representar graficamente$f$ em uma janela de visualização apropriada.

b. Use a$nDeriv$ função em uma calculadora gráfica para encontrar$f′(−4),\;f′(−2),\;f′(2)$,$f′(4)$ e.

Resposta

uma.

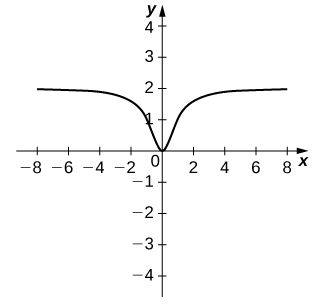
$A função começa no segundo quadrante e diminui suavemente, toca a origem e depois aumenta suavemente.$
b.$−0.028,−0.16,0.16,0.028$

\(x\)	\(Slope m_{PQ}\)	\(x\)	\(Slope m_{PQ}\)
1.1	(i)	0,9	(vii)
1,01	(ii)	0,99	(viii)
1.001	(iii)	0,999	(ix)
1.0001	(iv)	0,999	(x)
1.00001	(v)	0,9999	(xi)
1.000001	(vi)	0,999999	(xii)