3.1: Definindo a derivada

Last updated
Save as PDF

Page ID: 188493

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

objetivos de aprendizagem

Reconheça o significado da tangente a uma curva em um ponto.
Calcule a inclinação de uma reta tangente.
Identifique a derivada como o limite de um quociente de diferença.
Calcule a derivada de uma determinada função em um ponto.
Descreva a velocidade como uma taxa de variação.
Explique a diferença entre a velocidade média e a velocidade instantânea.
Estime a derivada de uma tabela de valores.

Agora que temos uma compreensão conceitual de um limite e a capacidade prática de calcular limites, estabelecemos a base para nosso estudo do cálculo, o ramo da matemática no qual calculamos derivadas e integrais. A maioria dos matemáticos e historiadores concorda que o cálculo foi desenvolvido de forma independente pelo inglês Isaac Newton (1643—1727) e pelo alemão Gottfried Leibniz (1646—1716), cujas imagens aparecem na Figura$\PageIndex{1}$. Quando creditamos a Newton e Leibniz o desenvolvimento do cálculo, estamos realmente nos referindo ao fato de que Newton e Leibniz foram os primeiros a entender a relação entre a derivada e a integral. Ambos os matemáticos se beneficiaram do trabalho de antecessores, como Barrow, Fermat e Cavalieri. A relação inicial entre os dois matemáticos parece ter sido amigável; no entanto, nos anos posteriores, surgiu uma amarga controvérsia sobre qual trabalho teve precedência. Embora pareça provável que Newton, de fato, tenha chegado primeiro às ideias por trás do cálculo, estamos em dívida com Leibniz pela notação que costumamos usar hoje.

Fotos de Newton e Leibniz. — Figura$\PageIndex{1}$: Newton e Leibniz são creditados por desenvolverem o cálculo de forma independente.

Linhas tangentes

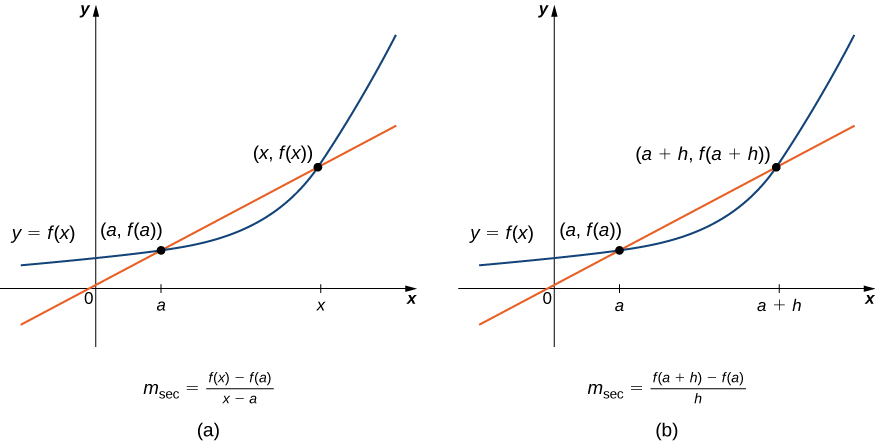
Começamos nosso estudo do cálculo revisitando a noção de retas secantes e retas tangentes. Lembre-se de que usamos a inclinação de uma linha secante para uma função em um ponto$(a,f(a))$ para estimar a taxa de mudança, ou a taxa na qual uma variável muda em relação a outra variável. Podemos obter a inclinação da secante escolhendo um valor de x próximo a e desenhando uma linha através dos pontos$(a,f(a))$ e$(x,f(x))$, conforme mostrado na Figura$\PageIndex{2}$. A inclinação dessa reta é dada por uma equação na forma de um quociente de diferença:

\[m_{sec}=\frac{f(x)−f(a)}{x−a} \nonumber \]

Também podemos calcular a inclinação de uma reta secante para uma função em um valor a usando essa equação e$x$ substituindo por$a+h$, onde$h$ é um valor próximo a a. Podemos então calcular a inclinação da linha através dos pontos$(a,f(a))$$(a+h,f(a+h))$ e. Nesse caso, descobrimos que a linha secante tem uma inclinação dada pelo seguinte quociente de diferença com incremento$h$:

\[m_{sec}=\frac{f(a+h)−f(a)}{a+h−a}=\frac{f(a+h)−f(a)}{h} \nonumber \]

Definição: Quociente de diferença

$f$Seja uma função definida em um intervalo$I$ contendo$a$. Se$x≠a$ estiver dentro$I$, então

\[Q=\frac{f(x)−f(a)}{x−a} \nonumber \]

é um quociente de diferença.

Além disso, se$h≠0$ for escolhido de forma que$a+h$ esteja em$I$, então

\[Q=\frac{f(a+h)−f(a)}{h} \nonumber \]

é um quociente de diferença com incremento$h$.

Essas duas expressões para calcular a inclinação de uma linha secante são ilustradas na Figura$\PageIndex{2}$. Veremos que cada um desses dois métodos para encontrar a inclinação de uma linha secante é valioso. Dependendo da configuração, podemos escolher uma ou outra. A principal consideração em nossa escolha geralmente depende da facilidade de cálculo.

alt — Figura$\PageIndex{2}$: Podemos calcular a inclinação de uma linha secante de duas maneiras.

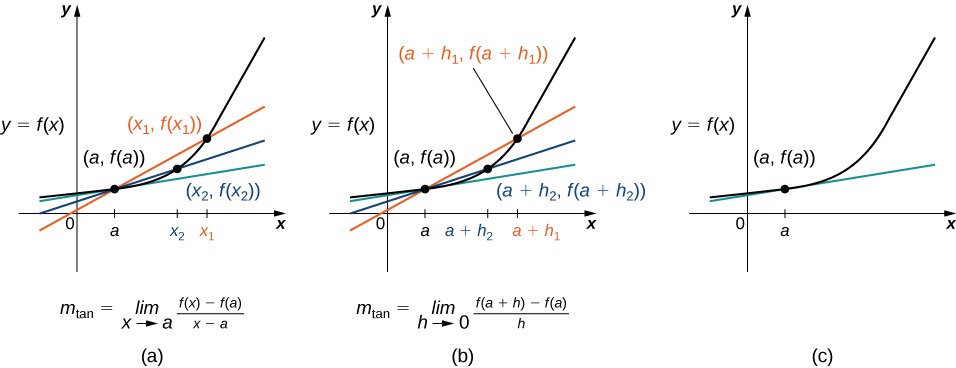
Na Figura,$\PageIndex{3a}$ vemos que, como valores de$x$ aproximação$a$, as inclinações das linhas secantes fornecem melhores estimativas da taxa de mudança da função em$a$. Além disso, as próprias linhas secantes se aproximam da reta tangente à função at$a$, que representa o limite das linhas secantes. Da mesma forma, a Figura$\PageIndex{3b}$ mostra que, à medida que os valores de$h$ se aproximam$0$, as linhas secantes também se aproximam da reta tangente. A inclinação da reta tangente em$a$ é a taxa de variação da função em$a$, conforme mostrado na Figura$\PageIndex{3c}$.

Esta figura consiste em três gráficos rotulados a, b e c. A Figura a mostra o plano de coordenadas cartesiano com 0, a, x2 e x1 marcados em ordem no eixo x. Há uma curva chamada y = f (x) com pontos marcados (a, f (a)), (x2, f (x2)) e (x1, f (x1)). Há três linhas retas: as primeiras cruzes (a, f (a)) e (x1, f (x1)); a segunda cruza (a, f (a)) e (x2, f (x2)); e a terceira toca apenas (a, f (a)), tornando-a a tangente. Na parte inferior do gráfico, a equação mtan = limx → a (f (x) - f (a))/(x - a) é fornecida. A Figura b mostra um gráfico semelhante, mas desta vez a + h2 e a + h1 estão marcados no eixo x em vez de x2 e x1. Consequentemente, a curva chamada y = f (x) passa por (a, f (a)), (a + h2, f (a + h2)) e (a + h1, f (a + h1)) e as linhas retas cruzam o gráfico da mesma forma que na Figura a. Na parte inferior do gráfico, a equação mtan = limh → 0 (f (a + h) - f (a)) /h é fornecido. A Figura c mostra apenas a curva rotulada y = f (x) e sua tangente no ponto (a, f (a)). — Figura$\PageIndex{3}$: As linhas secantes se aproximam da reta tangente (mostrada em verde) quando o segundo ponto se aproxima do primeiro.

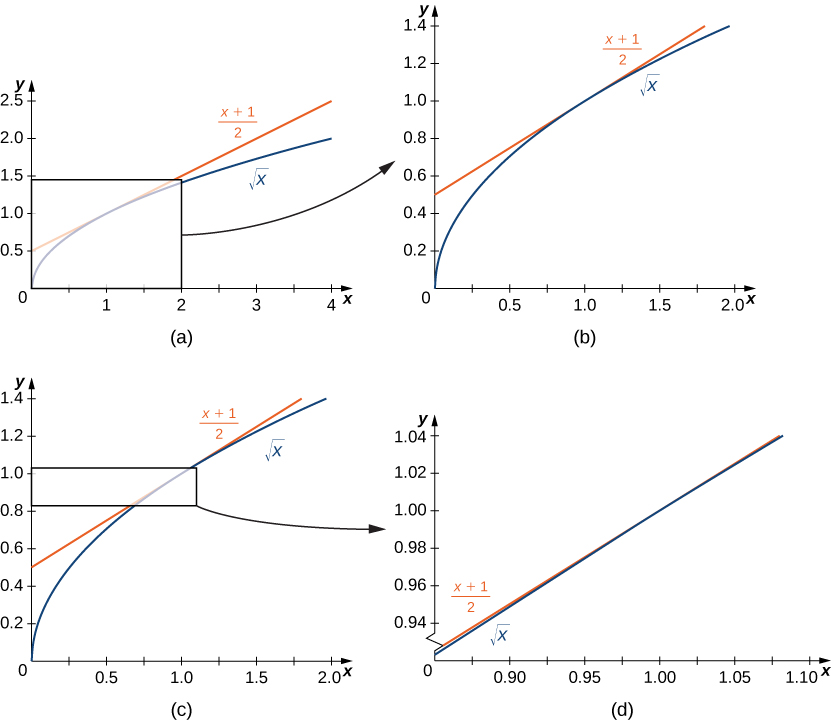
Na Figura,$\PageIndex{4}$ mostramos o gráfico$f(x)=\sqrt{x}$ e sua reta tangente$(1,1)$ em uma série de intervalos mais estreitos em torno de$x=1$. À medida que os intervalos se tornam mais estreitos, o gráfico da função e sua reta tangente parecem coincidir, tornando os valores na reta tangente uma boa aproximação aos valores da função para escolhas$x$ próximas$1$ a. De fato, o gráfico de$f(x)$ si mesmo parece ser localmente linear nas imediações de$x=1$.

Esta figura consiste em quatro gráficos rotulados a, b, c e d. A Figura a mostra os gráficos da raiz quadrada de x e a equação y = (x + 1) /2 com o eixo x indo de 0 a 4 e o eixo y indo de 0 a 2,5. Os gráficos dessas duas funções parecem muito próximos de 1; há uma caixa ao redor da qual esses gráficos olham de perto. A Figura b mostra um close up dessas mesmas duas funções na área da caixa da Figura a, especificamente x indo de 0 a 2 e y indo de 0 a 1,4. A Figura c é o mesmo gráfico da Figura b, mas este tem uma caixa de 0 a 1,1 na coordenada x e 0,8 e 1 na coordenada y. Há uma seta indicando que isso está ampliado na Figura d. A Figura d mostra uma imagem bem próxima da caixa da Figura c, e as duas funções parecem estar se tocando por quase todo o comprimento do gráfico. — Figura$\PageIndex{4}$: Para valores$x$ próximos a$1$, o gráfico$f(x)=\sqrt{x}$ e sua linha tangente parecem coincidir.

Formalmente, podemos definir a reta tangente ao gráfico de uma função da seguinte forma.

Definição: Linha tangente

$f(x)$Seja uma função definida em um intervalo aberto contendo$a$. A reta tangente a$f(x)$ at$a$ é a linha que passa pelo ponto$(a,f(a))$ com inclinação

\[m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{tanline1} \]

desde que esse limite exista.

Equivalentemente, podemos definir a reta tangente$a$ a$f(x)$ at como sendo a linha que passa pelo ponto$(a,f(a))$ com inclinação

\[m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h} \label{tanline2} \]

desde que esse limite exista.

Assim como usamos duas expressões diferentes para definir a inclinação de uma linha secante, usamos duas formas diferentes para definir a inclinação da reta tangente. Neste texto, usamos as duas formas da definição. Como antes, a escolha da definição dependerá da configuração. Agora que definimos formalmente uma reta tangente a uma função em um ponto, podemos usar essa definição para encontrar equações de retas tangentes.

Exemplo$\PageIndex{1}$: Finding a Tangent Line

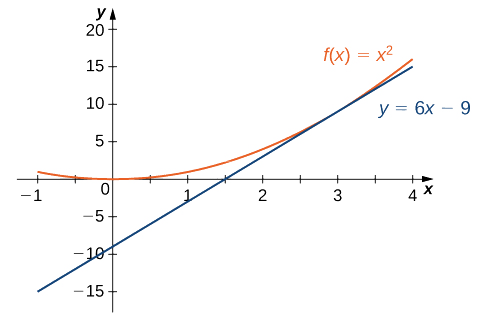
Encontre a equação da reta tangente ao gráfico de$f(x)=x^2$ em$x=3.$

Solução

Primeiro, encontre a inclinação da reta tangente. Neste exemplo, use Equation\ ref {tanline1}.

\ (\ displaystyle\ begin {align*} m_ {tan} &=\ lim_ {x→3}\ frac {f (x) −f (3)} {x−3} & &\ text {Aplique a definição.}\\ [4pt]
&=\ lim_ {x→3}\ frac {x^2−9} {x−3} & &\ text {Substitute} f (x) =x^2\ texto {e} f (3) =9\\ [4pt]
&=\ lim_ {x→3}\ frac {(x−3) (x+3)} {x−3} =\ lim_ {x→3} (x+3) =6 & ; &\ text {Fator o numerador para avaliar o limite.} \ end {align*}\)

Em seguida, encontre um ponto na reta tangente. Como a reta é tangente ao gráfico de$f(x)$ at$x=3$, ela passa pelo ponto$(3,f(3))$. Nós temos$f(3)=9$, então a reta tangente passa pelo ponto$(3,9)$.

Usando a equação ponto-inclinação da reta com a inclinação$m=6$ e o ponto$(3,9)$, obtemos a reta$y−9=6(x−3)$. Simplificando, nós temos$y=6x−9$. O gráfico de$f(x)=x^2$ e sua reta tangente em$3$ são mostrados na Figura$\PageIndex{5}$.

Esta figura consiste nos gráficos de f (x) = x ao quadrado e y = 6x - 9. Os gráficos dessas funções parecem tocar em x = 3. — Figura$\PageIndex{5}$: A reta tangente a$f(x)$ at$x=3$.

Exemplo$\PageIndex{2}$: The Slope of a Tangent Line Revisited

Use a Equação\ ref {tanline2} para encontrar a inclinação da reta tangente ao gráfico de$f(x)=x^2$ at$x=3$.

Solução

As etapas são muito semelhantes às do Example$\PageIndex{1}$. Consulte a Equação\ ref {tanline2} para obter a definição.

\ (\ begin {align*} m_ {tan} &=\ lim_ {h→0}\ frac {f (3+h) −f (3)} {h} & &\ text {Aplique a definição.}\\ [4pt]
&=\ lim_ {h→0}\ frac {(3+h) ^2−9} {h} & &\ text {Substitute} f (3+h) =( 3+h) ^2\ text {e} f (3) =9\\ [4pt]
&=\ lim_ {h→0}\ frac {9+6h+h^2−9} {h} & &\ text {Expandir e simplifique para avaliar o limite.}\\ [4pt]
&=\ lim_ {h→0}\ frac {h (6+h)} {h} =\ lim_ {h→0} (6+h) =6\ end {align*}\)

Obtivemos o mesmo valor para a inclinação da reta tangente usando a outra definição, demonstrando que as fórmulas podem ser trocadas.

Exemplo$\PageIndex{3}$: Finding the Equation of a Tangent Line

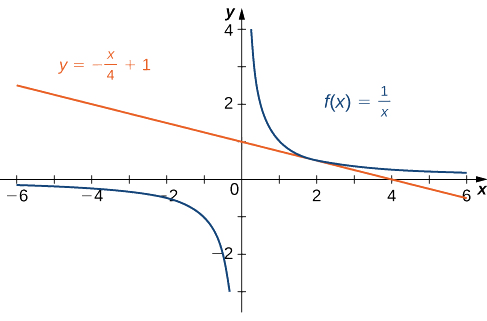
Encontre a equação da reta tangente ao gráfico de$f(x)=1/x$ at$x=2$.

Solução

Podemos usar a Equação\ ref {tanline1}, mas, como vimos, os resultados são os mesmos se usarmos a Equação\ ref {tanline2}.

\ (\ displaystyle\ begin {align*} m_ {tan} &=\ lim_ {x→2}\ frac {f (x) −f (2)} {x−2} & &\ text {Aplique a definição.}\\ [4pt]
&=\ lim_ {x→2}\ frac {\ frac {1} {x} −\ frac {1} {x} −\ frac {1} {x} −\ frac {1} {x} −\ frac {1} {x} −\ frac {1} {x}} {x−2} & &\ text {Substituto} f (x) =\ frac {1} {x}\ texto {e} f (2) =\ frac {1} {2}\\ [4pt]
&=\ lim_ {x→2}\ frac {\ frac {1} {x} −\ frac {1} {2}} {x−2} ‣\ frac {2x} {2x} & &\ text {Multiplique o numerador e o denominador por} 2x\ text {para simplificar frações.}\\ [4pt]
&=\ lim_ {x→2}\ frac {(2−x)} {(x−2) (2−x)} {(x−2) x)} & &\ text {Simplifique.}\\ [4pt]
&=\ lim_ {x→2}\ frac {−1} {2x} & &\ text {Simplifique usando}\ frac {2−x} {x−2} =−1,\ text {for} x≠ 2.\\ [4pt]
&=−\ frac {1} {4} & &\ text {Avalie o limite.} \ end {align*}\)

Agora sabemos que a inclinação da reta tangente é$−\frac{1}{4}$. Para encontrar a equação da reta tangente, também precisamos de um ponto na reta. Nós sabemos disso$f(2)=\frac{1}{2}$. Como a reta tangente passa pelo ponto,$(2,\frac{1}{2})$ podemos usar a equação ponto-inclinação de uma reta para encontrar a equação da reta tangente. Assim, a reta tangente tem a equação$y=−\frac{1}{4}x+1$. Os gráficos de$f(x)=\frac{1}{x}$ e$y=−\frac{1}{4}x+1$ são mostrados na Figura$\PageIndex{6}$.

Esta figura consiste nos gráficos de f (x) = 1/x e y = -x/4 + 1. A parte do gráfico f (x) = 1/x no primeiro quadrante parece tocar o gráfico da outra função em x = 2. — Figura: A$\PageIndex{6}$ linha é tangente a at$f(x)$.$x=2$

Exercício$\PageIndex{1}$

Encontre a inclinação da reta tangente ao gráfico de$f(x)=\sqrt{x}$ at$x=4$.

Dica: Use a Equação\ ref {tanline1} ou a Equação\ ref {tanline2}. Multiplique o numerador e o denominador por um conjugado.

Resposta: $\frac{1}{4}$

A derivada de uma função em um ponto

O tipo de limite que calculamos para encontrar a inclinação da reta tangente a uma função em um ponto ocorre em muitas aplicações em várias disciplinas. Essas aplicações incluem velocidade e aceleração em física, funções de lucro marginal nos negócios e taxas de crescimento em biologia. Esse limite ocorre com tanta frequência que damos a esse valor um nome especial: a derivada. O processo de encontrar uma derivada é chamado de diferenciação.

Definição: Derivada

$f(x)$Seja uma função definida em um intervalo aberto contendo$a$. A derivada da função$f(x)$ at$a$, denotada por$f′(a)$, é definida por

\[f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{der1} \]

desde que esse limite exista.

Alternativamente, também podemos definir a derivada de$f(x)$ at$a$ como

\[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \label{der2} \]

Exemplo$\PageIndex{4}$: Estimating a Derivative

Para$f(x)=x^2$, use uma tabela para estimar$f′(3)$ usando a Equação\ ref {der1}.

Solução

Crie uma tabela usando valores$x$ logo abaixo$3$ e logo acima$3$.

$x$	$\dfrac{x^2−9}{x−3}$
\ (x\)” style="text-align:center; ">2.9	\ (\ dfrac {x^2−9} {x−3}\)” style="text-align:center; ">5.9
\ (x\)” style="text-align:center; ">2,99	\ (\ dfrac {x^2−9} {x−3}\)” style="text-align:center; ">5.99
\ (x\)” style="text-align:center; ">2.999	\ (\ dfrac {x^2−9} {x−3}\)” style="text-align:center; ">5.999
\ (x\)” style="text-align:center; ">3.001	\ (\ dfrac {x^2−9} {x−3}\)” style="text-align:center; ">6.001
\ (x\)” style="text-align:center; ">3.01	\ (\ dfrac {x^2−9} {x−3}\)” style="text-align:center; ">6.01
\ (x\)” style="text-align:center; ">3.1	\ (\ dfrac {x^2−9} {x−3}\)” style="text-align:center; ">6.1

Depois de examinar a tabela, vemos que uma boa estimativa é$f′(3)=6$.

Exercício$\PageIndex{2}$

Para$f(x)=x^2$, use uma tabela para estimar$f′(3)$ usando a Equação\ ref {der2}.

Dica: Avalie$\dfrac{(x+h)^2−x^2}{h}$ em$h=−0.1,\,−0.01,\,−0.001,\,0.001,\,0.01,\,0.1$

Resposta: 6

Exemplo$\PageIndex{6}$: Finding a Derivative

Para$f(x)=3x^2−4x+1$, encontre$f′(2)$ usando Equation\ ref {der1}.

Solução

Substitua a função e o valor fornecidos diretamente na equação.

\ (\ displaystyle\ begin {align*} f′( x) &=\ lim_ {x→2}\ frac {f (x) −f (2)} {x−2} & &\ text {Aplique a definição.}\\ [4pt]
&=\ lim_ {x→2}\ frac {(3x^2−4x+1) −5} {x−2} & &\ text {Substituto} f (x) =3x^2−4x+1\ texto {e} f (2) =5.\\ [4pt]
&=\ lim_ {x→2}\ frac {(x−2) (3x+2)} {x−2} & & amp;\ text {Simplifique e fatore o numerador.}\\ [4pt]
&=\ lim_ {x→2} (3x+2) & &\ text {Cancele o fator comum.}\\ [4pt]
&=8 & &\ text {Avalie o limite.} \ end {align*}\)

Exemplo$\PageIndex{7}$: Revisiting the Derivative

Para$f(x)=3x^2−4x+1$, encontre$f′(2)$ usando Equation\ ref {der2}.

Solução

Usando essa equação, podemos substituir dois valores da função na equação e devemos obter o mesmo valor de Example$\PageIndex{6}$.

\ (\ displaystyle\ begin {align*} f′( 2) &=\ lim_ {h→0}\ frac {f (2+h) −f (2)} {h} & &\ text {Aplique a definição.}\\ [4pt]
&=\ lim_ {h→0}\ frac {(3 (2+h) ^2−4 (2+h) +1) −5} {h} & &\ texto {Substituto} f (2) =5\ texto {e} f (2+h) =3 (2+h) ^2−4 (2+h) +1.\\ [4pt]
&=\ lim_ {h→0}\ frac {3 (4+4h+h^2) -8-4h+1-5} {h} & &\ text {Expanda o numerador.}\\ [4pt]
&=\ lim_ {h→0}\ frac {12+12h+3h^2-12-4h} {h} & &\ text {Distribua e comece a simplificar o numerador.}\\ [4pt]
&=\ lim_ {h→0}\ frac {3h→ ^2+8h} {h} & &\ text {Concluir a simplificação do numerador.}\\ [4pt]
&=\ lim_ {h→0}\ frac {h (3h+8)} {h} & &\ text {Fator o numerador.}\\ [4pt]
&=\ lim_ {h→0} (3h+8) & &\ text {Cancelar o fator comum.}\\ [4pt]
&=8 & &\ text {Avalie o limite.} \ end {align*}\)

Os resultados são os mesmos se usarmos a Equação\ ref {der1} ou a Equação\ ref {der2}.

Exercício$\PageIndex{4}$

Para$f(x)=x^2+3x+2$, encontre$f′(1)$.

Dica: Use a Equação\ ref {der1}, a Equação\ ref {der2} ou tente as duas.

Resposta: $f′(1)=5$

Velocidades e taxas de mudança

Agora que podemos calcular uma derivada, podemos usá-la em aplicações de velocidade. Lembre-se de que se$s(t)$ é a posição de um objeto se movendo ao longo de um eixo coordenado, a velocidade média do objeto em um intervalo de tempo,$[a,t]$ se$t>a$ ou$[t,a]$ se,$t<a$ é dada pelo quociente de diferença

\[v_{ave}=\frac{s(t)−s(a)}{t−a}. \label{avgvel} \]

Como valores de$t$ aproximação$a$, os valores de$v_{ave}$ aproximação são o valor em que chamamos de velocidade instantânea$a$. Ou seja, a velocidade instantânea em$a$, denotada$v(a)$, é dada por

\[v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \label{instvel} \]

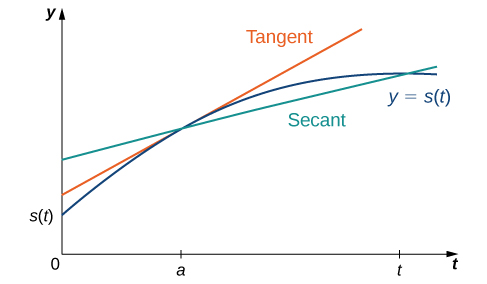
Para entender melhor a relação entre a velocidade média e a velocidade instantânea, veja a Figura$\PageIndex{7}$. Nesta figura, a inclinação da reta tangente (mostrada em vermelho) é a velocidade instantânea do objeto no momento,$t=a$ cuja posição no momento$t$ é dada pela função$s(t)$. A inclinação da linha secante (mostrada em verde) é a velocidade média do objeto ao longo do intervalo de tempo$[a,t]$.

Esta figura consiste no plano de coordenadas cartesiano com 0, a e t1 marcados no eixo t. A função y = s (t) é representada graficamente no primeiro quadrante junto com duas linhas marcadas como tangente e secante. A reta tangente toca y = s (t) em apenas um ponto, (a, s (a)). A linha secante toca y = s (t) em dois pontos: (a, s (a)) e (t1, s (t1)). — Figura$\PageIndex{7}$: A inclinação da linha secante é a velocidade média ao longo do intervalo$[a,t]$. A inclinação da reta tangente é a velocidade instantânea.

Podemos usar a Equação\ ref {instvel} para calcular a velocidade instantânea, ou podemos estimar a velocidade de um objeto em movimento usando uma tabela de valores. Em seguida, podemos confirmar a estimativa usando a Equação\ ref {avgvel}.

Exemplo$\PageIndex{8}$: Estimating Velocity

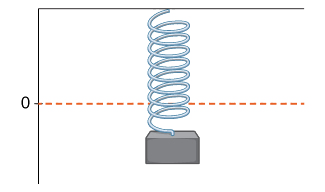
Um peso de chumbo em uma mola está oscilando para cima e para baixo. Sua posição no momento em$t$ relação a uma linha horizontal fixa é dada por$s(t)=\sin t$ (Figura$\PageIndex{8}$). Use uma tabela de valores para estimar$v(0)$. Verifique a estimativa usando a Equação\ ref {instvel}.

Uma foto de uma mola pendurada com um peso na ponta. Há uma linha tracejada horizontal marcada com 0 um pouco acima do peso. — Figura$\PageIndex{8}$: Um peso de chumbo suspenso de uma mola em movimento oscilatório vertical.

Solução

Podemos estimar a velocidade instantânea em$t=0$ computando uma tabela de velocidades médias usando valores de$t$ aproximação$0$, conforme mostrado na Tabela$\PageIndex{2}$.

Tabela$\PageIndex{2}$: Velocidades médias usando valores de$t$ aproximação de 0
$t$	$\frac{\sin t−\sin 0}{t−0}=\frac{\sin t}{t}$
\ (t\)” style="text-align:center; ">−0.1	\ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)” style="text-align:center; ">0.998334166
\ (t\)” style="text-align:center; ">−0.01	\ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)” style="text-align:center; ">0.9999833333
\ (t\)” style="text-align:center; ">−0.001	\ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)” style="text-align:center; ">0.999999833
\ (t\)” style="text-align:center; ">0.001	\ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)” style="text-align:center; ">0.999999833
\ (t\)” style="text-align:center; ">0,01	\ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)” style="text-align:center; ">0.9999833333
\ (t\)” style="text-align:center; ">0.1	\ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)” style="text-align:center; ">0.998334166

Na tabela, vemos que a velocidade média ao longo do intervalo de tempo$[−0.1,0]$ é$0.998334166$, a velocidade média ao longo do intervalo de tempo$[−0.01,0]$ é$0.9999833333$, e assim por diante. Usando essa tabela de valores, parece que uma boa estimativa é$v(0)=1$.

Usando Equation\ ref {instvel}, podemos ver que

\[v(0)=s′(0)=\lim_{t→0}\frac{\sin t−\sin 0}{t−0}=\lim_{t→0}\frac{\sin t}{t}=1. \nonumber \]

Assim, na verdade,$v(0)=1$.

Exercício$\PageIndex{5}$

Uma pedra é lançada de uma altura de$64$ pés. Sua altura acima do solo,$t$ segundos depois, é dada por$s(t)=−16t^2+64,\;0≤t≤2$. Encontre sua velocidade instantânea um$1$ segundo depois de cair, usando a Equação\ ref {instvel}.

Dica: $v(t)=s′(t)$. Siga os exemplos anteriores da derivada usando Equation\ ref {instvel}.

Resposta: −32 pés/s

Como vimos ao longo desta seção, a inclinação de uma reta tangente a uma função e a velocidade instantânea são conceitos relacionados. Cada um é calculado computando uma derivada e cada um mede a taxa instantânea de mudança de uma função ou a taxa de mudança de uma função em qualquer ponto ao longo da função.

Definição: Taxa de variação instantânea

A taxa instantânea de mudança de uma função$f(x)$ em um valor$a$ é sua derivada$f′(a)$.

Exemplo$\PageIndex{9}$: Chapter Opener: Estimating Rate of Change of Velocity

Atingindo uma velocidade máxima de$270.49$ mph, o Hennessey Venom GT é um dos carros mais rápidos do mundo. Nos testes, passou de$0$ para$60$ mph em$3.05$ segundos, de$0$ para$100$ mph em$5.88$ segundos, de$0$ para$200$ mph em$14.51$ segundos, e de$0$ para$229.9$ mph em$19.96$ segundos. Use esses dados para tirar uma conclusão sobre a taxa de mudança de velocidade (ou seja, sua aceleração) à medida que ela se aproxima de$229.9$ mph. A taxa na qual o carro está acelerando parece estar aumentando, diminuindo ou constante?

O mesmo carro esportivo correndo por uma estrada sinuosa desde o início do capítulo. — Figura$\PageIndex{9}$: (crédito: modificação do trabalho pelo Codex41, Flickr)

Solução: Primeiro, observe que$60$ mph =$88$ ft/s,$100$ mph ≈$146.67$ pés/s,$200$ mph ≈$293.33$ pés/s e$229.9$ mph ≈$337.19$ pés/s. Podemos resumir as informações em uma tabela.

Tabela$\PageIndex{3}$: $v(t)$ em diferentes valores de$t$
$t$	$v(t)$
\ (t\) ">0	\ (v (t)\) ">0
\ (t\) ">3,05	\ (v (t)\) ">88
\ (t\) ">5,88	\ (v (t)\) ">147,67
\ (t\) ">14,51	\ (v (t)\) ">293,33
\ (t\) ">19,96	\ (v (t)\) ">337,19

Agora, calcule a aceleração média do carro em pés por segundo em intervalos do formulário à$[t,19.96]$ medida que$t$ se aproxima$19.96$, conforme mostrado na tabela a seguir.

Aceleração média
$t$	$\dfrac{v(t)−v(19.96)}{t−19.96}=\dfrac{v(t)−337.19}{t−19.96}$
\ (t\) ">0,0	\ (\ dfrac {v (t) −v (19,96)} {t−19,96} =\ dfrac {v (t) −337,19} {t−19,96}\) ">16,89
\ (t\) ">3,05	\ (\ dfrac {v (t) −v (19,96)} {t−19,96} =\ dfrac {v (t) −337,19} {t−19,96}\) ">14,74
\ (t\) ">5,88	\ (\ dfrac {v (t) −v (19,96)} {t−19,96} =\ dfrac {v (t) −337,19} {t−19,96}\) ">13,46
\ (t\) ">14,51	\ (\ dfrac {v (t) −v (19,96)} {t−19,96} =\ dfrac {v (t) −337,19} {t−19,96}\) ">8,05

A taxa na qual o carro está acelerando está diminuindo à medida que sua velocidade se aproxima de$229.9$ mph ($337.19$ft/s).

Exemplo$\PageIndex{10}$: Rate of Change of Temperature

Um proprietário ajusta o termostato para que a temperatura na casa comece a cair a partir da$70°F$$9$ tarde, atinja o mínimo$60°$ durante a noite e volte para a$70°$$7$ manhã da manhã seguinte. Suponha que a temperatura na casa seja dada$T(t)=0.4t^2−4t+70$ por for$0≤t≤10$, onde$t$ está o número de horas após a$9$ tarde. Encontre a taxa instantânea de mudança da temperatura à meia-noite.

Solução

Como a meia-noite passa$3$ horas da$9$ tarde, queremos computar$T′(3)$. Consulte a Equação\ ref {der1}.

\ (\ displaystyle\ begin {align*} T′( 3) &=\ lim_ {t→3}\ frac {T (t) −T (3)} {t−3} & &\ text {Aplique a definição.}\\ [4pt]
&=\ lim_ {t→3}\ frac {0.4t^2−4t+70−61.6} {t−3} & &\ text {Substituto} T (t) =0,4t^2−4t+70\ texto {e} T (3) =61,6.\\ [4pt]
&=\ lim_ {t→3}\ frac {0,4t^2−4t+8,4} {t− 3} & &\ text {Simplifique.}\\ [4pt]
&=\ lim_ {t→3}\ frac {0.4 (t−3) (t−7)} {t−3}\\ [4pt]
&=\ lim_ {t→3} 0.4 (t−7) & &\ text {Cancelar.}\\ [4pt]
&=−1,6 & &\ text {Avalie o limite.} \ end {align*}\)

A taxa instantânea de mudança da temperatura à meia-noite é$−1.6°F$ por hora.

Exemplo$\PageIndex{11}$: Rate of Change of Profit

Uma empresa de brinquedos pode vender sistemas de jogos$x$ eletrônicos a um preço de$p=−0.01x+400$ dólares por sistema de jogo. O custo dos$x$ sistemas de fabricação é dado em$C(x)=100x+10,000$ dólares. Encontre a taxa de variação do lucro quando os$10,000$ jogos são produzidos. A empresa de brinquedos deve aumentar ou diminuir a produção?

Solução

O lucro$P(x)$ obtido com a produção de sistemas de$x$ jogos é$R(x)−C(x)$: onde$R(x)$ está a receita obtida com a venda de$x$ jogos. Como a empresa pode vender$x$ jogos$p=−0.01x+400$ por jogo,

$R(x)=xp=x(−0.01x+400)=−0.01x^2+400x$.

Consequentemente,

$P(x)=−0.01x^2+300x−10,000$.

Portanto, avaliar a taxa de variação do lucro dá

\ (\ displaystyle\ begin {align*} P′( 10000) &=\ lim_ {x→10000}\ frac {P (x) −P (10000)} {x−10000}\ [4pt]
&=\ lim_ {x→10000}\ frac {−0,01x^2+300x−10000−1990000} {x−10000} {x−10000}\ [4pt]
&=\ lim_ {x→10000}\ frac {−0,01x^2+300x−2000000} {x−10000}\\ [4pt]
&=100\ end {align*}\).

Desde a taxa de variação do lucro$P′(10,000)>0$ e$P(10,000)>0$, a empresa deve aumentar a produção.

Exercício$\PageIndex{6}$

Uma cafeteria determina que o lucro diário dos scones obtido ao cobrar um dólar por bolinho é$P(s)=−20s^2+150s−10$. Atualmente, a cafeteria cobra$$3.25$ por bolinho. Encontre$P′(3.25)$ a taxa de variação do lucro quando o preço é$$3.25$ e decida se a cafeteria deve ou não considerar aumentar ou diminuir seus preços em scones.

Dica: Use o Exemplo$\PageIndex{11}$ como guia.

Resposta: $P′(3.25)=20>0$; aumentar os preços

Conceitos-chave

A inclinação da reta tangente a uma curva mede a taxa instantânea de variação de uma curva. Podemos calculá-lo encontrando o limite do quociente de diferença ou o quociente de diferença com incremento$h$.
A derivada de uma função$f(x)$ em um valor$a$ é encontrada usando qualquer uma das definições para a inclinação da reta tangente.
A velocidade é a taxa de mudança de posição. Como tal, a velocidade$v(t)$ no tempo$t$ é a derivada da posição$s(t)$ no tempo$t$.
A velocidade média é dada por A velocidade\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \nonumber \] instantânea é dada por\[\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \nonumber \]
Podemos estimar uma derivada usando uma tabela de valores.

Equações-chave

Quociente de diferença

$Q=\dfrac{f(x)−f(a)}{x−a}$

Quociente de diferença com incremento h

$Q=\dfrac{f(a+h)−f(a)}{a+h−a}=\dfrac{f(a+h)−f(a)}{h}$

Inclinação da reta tangente

$\displaystyle m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a}$

$\displaystyle m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h}$

Derivada de f (x) em a

$\displaystyle f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a}$

$\displaystyle f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}$

Velocidade média

$v_{ave}=\dfrac{s(t)−s(a)}{t−a}$

Velocidade instantânea

$\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}$

Glossário

derivado: a inclinação da reta tangente a uma função em um ponto, calculada tomando o limite do quociente de diferença, é a derivada

quociente de diferença

de uma função$f(x)$ at$a$ é dada por

$\dfrac{f(a+h)−f(a)}{h}$ou$\dfrac{f(x)−f(a)}{x−a}$

diferenciação: o processo de obtenção de um derivado

taxa instantânea de mudança: a taxa de variação de uma função em qualquer ponto ao longo da função$a$, também chamada$f′(a)$, ou a derivada da função em$a$

Definição: Quociente de diferença

Definição: Linha tangente

Exemplo\(\PageIndex{1}\): Finding a Tangent Line

Exemplo\(\PageIndex{2}\): The Slope of a Tangent Line Revisited

Exemplo\(\PageIndex{3}\): Finding the Equation of a Tangent Line

Exercício\(\PageIndex{1}\)

Definição: Derivada

Exemplo\(\PageIndex{4}\): Estimating a Derivative

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{6}\): Finding a Derivative

Exemplo\(\PageIndex{7}\): Revisiting the Derivative

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{8}\): Estimating Velocity

Exercício\(\PageIndex{5}\)

Definição: Taxa de variação instantânea

Exemplo\(\PageIndex{9}\): Chapter Opener: Estimating Rate of Change of Velocity

Exemplo\(\PageIndex{10}\): Rate of Change of Temperature

Exemplo\(\PageIndex{11}\): Rate of Change of Profit

Exercício\(\PageIndex{6}\)