2.4: Continuidade

Last updated
Save as PDF

Page ID: 188675

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Explique as três condições para continuidade em um ponto.
Descreva três tipos de descontinuidades.
Defina a continuidade em um intervalo.
Declare o teorema para limites de funções compostas.
Forneça um exemplo do teorema do valor intermediário.

Muitas funções têm a propriedade de que seus gráficos podem ser traçados com um lápis sem levantar o lápis da página. Essas funções são chamadas de contínuas. Outras funções têm pontos nos quais ocorre uma quebra no gráfico, mas satisfazem essa propriedade em intervalos contidos em seus domínios. Eles são contínuos nesses intervalos e dizem que apresentam uma descontinuidade no ponto em que ocorre uma interrupção.

Começamos nossa investigação sobre continuidade explorando o que significa para uma função ter continuidade em um ponto. Intuitivamente, uma função é contínua em um determinado ponto se não houver quebra em seu gráfico nesse ponto.

Continuidade em um ponto

Antes de analisarmos uma definição formal do que significa para uma função ser contínua em um ponto, vamos considerar várias funções que não atendem à nossa noção intuitiva do que significa ser contínua em um ponto. Em seguida, criamos uma lista de condições que evitam tais falhas.

Nossa primeira função de interesse é mostrada na Figura\(\PageIndex{1}\). Vemos que o gráfico de\(f(x)\) tem um furo em\(a\). Na verdade,\(f(a)\) é indefinido. No mínimo,\(f(x)\) para ser contínuo em\(a\), precisamos da seguinte condição:

i.\(f(a)\) é definido

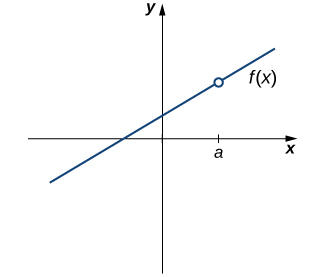
Um gráfico de uma função linear crescente f (x) que cruza o eixo x do quadrante três ao quadrante dois e que cruza o eixo y do quadrante dois ao quadrante um. Um ponto maior que zero é marcado no eixo x. O ponto na função f (x) acima de a é um círculo aberto; a função não está definida em a. — Figura\(\PageIndex{1}\): A função não\(f(x)\) é contínua em\(a\) porque\(f(a)\) é indefinida.

No entanto, como vemos na Figura\(\PageIndex{2}\), essa condição por si só é insuficiente para garantir a continuidade no momento\(a\). Embora\(f(a)\) esteja definida, a função tem uma lacuna em\(a\). Neste exemplo, a lacuna existe porque\(\displaystyle \lim_{x→a}f(x)\) não existe. Devemos adicionar outra condição para continuidade em\(a\) — a saber,

ii. \(\displaystyle \lim_{x→a}f(x)\)existe

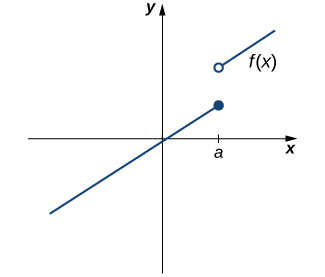
O gráfico de uma função por partes f (x) com duas partes. A primeira parte é uma função linear crescente que cruza do quadrante três para o quadrante um na origem. Um ponto maior que zero é marcado no eixo x. Em fa. neste segmento, há um círculo sólido. O outro segmento também é uma função linear crescente. Ela existe no quadrante um para valores de x maiores que a. Em x=a, esse segmento tem um círculo aberto. — Figura\(\PageIndex{2}\): A função não\(f(x)\) é contínua em\(a\) porque\(\displaystyle \lim_{x→a}f(x)\) não existe.

No entanto, como vemos na Figura\(\PageIndex{3}\), essas duas condições por si só não garantem a continuidade em um determinado ponto. A função nesta figura satisfaz as duas primeiras condições, mas ainda não é contínua em\(a\). Devemos adicionar uma terceira condição à nossa lista:

iii. \(\displaystyle \lim_{x→a}f(x)=f(a)\)

O gráfico de uma função por partes com duas partes. A primeira parte é uma função linear crescente que cruza o eixo x do quadrante três ao quadrante dois e que cruza o eixo y do quadrante dois ao quadrante um. Um ponto maior que zero é marcado no eixo x. Neste ponto, há um círculo aberto na função linear. A segunda parte é um ponto em x=a acima da linha. — Figura\(\PageIndex{3}\): A função não\(f(x)\) é contínua\(a\) porque\(\displaystyle \lim_{x→a}f(x)≠f(a)\).

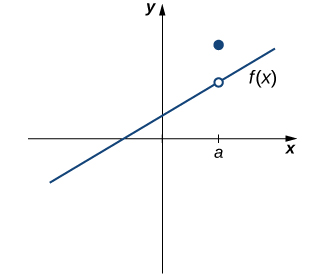
Agora juntamos nossa lista de condições e formamos uma definição de continuidade em um ponto.

Definição: Contínuo em um ponto

Uma função\(f(x)\) é contínua em um ponto \(a\)se e somente se as três condições a seguir forem satisfeitas:

\(f(a)\)é definido
\(\displaystyle \lim_{x→a}f(x)\)existe
\(\displaystyle \lim_{x→a}f(x)=f(a)\)

Uma função é descontínua em um ponto\(a\) se não for contínua em\(a\).

O procedimento a seguir pode ser usado para analisar a continuidade de uma função em um ponto usando essa definição.

Estratégia de resolução de problemas: determinando a continuidade em um ponto

Verifique se\(f(a)\) está definido. Se\(f(a)\) for indefinido, não precisamos ir mais longe. A função não é contínua em\(a.\) Se\(f(a)\) for definida, continue até a etapa 2.
Computar\(\displaystyle \lim_{x→a}f(x)\). Em alguns casos, talvez precisemos fazer isso primeiro computando\(\displaystyle \lim_{x→a^−}f(x)\)\(\displaystyle \lim_{x→a^+}f(x)\) e. Se\(\displaystyle \lim_{x→a}f(x)\) não existe (ou seja, não é um número real), a função não é contínua em\(a\) e o problema está resolvido. Se\(\displaystyle \lim_{x→a}f(x)\) existir, continue com a etapa 3.
Compare\(f(a)\)\(\displaystyle \lim_{x→a}f(x)\) e. Se\(\displaystyle \lim_{x→a}f(x)≠f(a)\), então a função não é contínua em\(a.\) If\(\displaystyle \lim_{x→a}f(x)=f(a)\), então a função é contínua em\(a.\)

Os próximos três exemplos demonstram como aplicar essa definição para determinar se uma função é contínua em um determinado ponto. Esses exemplos ilustram situações em que cada uma das condições de continuidade na definição é bem-sucedida ou falha.

Exemplo\(\PageIndex{1A}\): Determining Continuity at a Point, Condition 1

Usando a definição, determine se a função\(f(x)=\dfrac{x^2−4}{x−2}\) é contínua em\(x=2\). Justifique a conclusão.

Solução

Vamos começar tentando calcular\(f(2)\). Podemos ver isso\(f(2)=0/0\), que é indefinido. Portanto,\(f(x)=\dfrac{x^2−4}{x−2}\) é descontínuo em\(2\) porque\(f(2)\) é indefinido. O gráfico de\(f(x)\) é mostrado na Figura\(\PageIndex{4}\).

Um gráfico da função dada. Há uma linha que cruza o eixo x do quadrante três ao quadrante dois e que cruza o eixo y do quadrante dois ao quadrante um. Em um ponto no quadrante um, há um círculo aberto onde a função não está definida. — Figura\(\PageIndex{4}\): A função\(f(x)\) é descontínua em\(2\) porque\(f(2)\) é indefinida.

Exemplo\(\PageIndex{1B}\): Determining Continuity at a Point, Condition 2

Usando a definição, determine se a função\(f(x)=\begin{cases}−x^2+4, & \mathrm{if} \; x≤3 \\ 4x−8, & \mathrm{if} \; x>3\end{cases}\) é contínua em\(x=3\). Justifique a conclusão.

Solução

Vamos começar tentando calcular\(f(3)\).

\(f(3)=−(3^2)+4=−5\).

Assim,\(f(3)\) está definido. Em seguida, calculamos\(\displaystyle \lim_{x→3}f(x)\). Para fazer isso, precisamos computar\(\displaystyle \lim_{x→3^−}f(x)\) e\( \displaystyle \lim_{x→3^+}f(x)\):

\(\displaystyle \lim_{x→3^−}f(x)=−(3^2)+4=−5\)

\(\displaystyle \lim_{x→3^+}f(x)=4(3)−8=4\).

Portanto,\(\displaystyle \lim_{x→3}f(x)\) não existe. Assim, não\(f(x)\) é contínuo em 3. O gráfico de\(f(x)\) é mostrado na Figura\(\PageIndex{5}\).

Um gráfico de uma determinada função por partes, que tem duas partes. A primeira é uma parábola de abertura descendente que é simétrica em relação ao eixo y. Seu vértice está no eixo y, maior que zero. Há um círculo fechado na parábola para x=3. A segunda parte é uma função linear crescente no primeiro quadrante, que existe para valores de x — Figura\(\PageIndex{5}\): A função não\(f(x)\) é contínua em 3 porque\(\displaystyle \lim_{x→3}f(x)\) não existe.

Exemplo\(\PageIndex{1C}\): Determining Continuity at a Point, Condition 3

Usando a definição, determine se a função\(f(x)=\begin{cases}\frac{\sin x}{x}, & \text{if } x≠0\\1, & \text{if } x=0\end{cases}\) é contínua em\(x=0\).

Solução

Primeiro, observe que

\(f(0)=1\)

Em seguida,

\(\displaystyle \lim_{x→0}f(x)=\lim_{x→0}\frac{\sin x}{x}=1\).

Por último, compare\(f(0)\)\(\displaystyle \lim_{x→0}f(x)\) e. Nós vemos isso

\(\displaystyle f(0)=1=\lim_{x→0}f(x)\).

Como todas as três condições na definição de continuidade são satisfeitas,\(f(x)\) é contínuo em\(x=0\).

Exercício\(\PageIndex{1}\)

Usando a definição, determine se a função\(f(x)=\begin{cases}2x+1, & \text{if }x<1\\2, & \text{if }x=1\\ −x+4, & \text{if }x>1\end{cases}\) é contínua em\(x=1\). Se a função não for contínua em 1, indique a condição para continuidade em um ponto que não se mantenha.

Dica: Verifique cada condição da definição.

Resposta: \(f\)não é contínuo\(1\) porque\(\displaystyle f(1)=2≠3=\lim_{x→1}f(x)\).

Ao aplicar a definição de continuidade e teoremas previamente estabelecidos sobre a avaliação de limites, podemos afirmar o seguinte teorema.

Teorema\(\PageIndex{1}\): Continuity of Polynomials and Rational Functions

Polinômios e funções racionais são contínuos em cada ponto de seus domínios.

Prova

Anteriormente, mostramos que se\(p(x)\) e\(q(x)\) são polinômios,\(\displaystyle \lim_{x→a}p(x)=p(a)\) para cada polinômio\(p(x)\) e\(\displaystyle \lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}\) tão longos quanto\(q(a)≠0\). Portanto, polinômios e funções racionais são contínuos em seus domínios.

□

Agora aplicamos o Teorema\(\PageIndex{1}\) para determinar os pontos nos quais uma determinada função racional é contínua.

Exemplo\(\PageIndex{2}\):Continuity of a Rational Function

Para quais valores de x são\(f(x)=\dfrac{x+1}{x−5}\) contínuos?

Solução

A função racional\(f(x)=\dfrac{x+1}{x−5}\) é contínua para cada valor de\(x\), exceto\(x=5\).

Exercício\(\PageIndex{2}\)

Para quais valores de\(x\) é\(f(x)=3x^4−4x^2\) contínuo?

Dica: Use a Continuidade de Polinômios e Funções Racionais mencionadas acima.

Resposta: \(f(x)\)é contínuo em cada número real.

Tipos de descontinuidades

Como vimos em Exemplo\(\PageIndex{1A}\) e Exemplo\(\PageIndex{1B}\), as descontinuidades assumem várias aparências diferentes. Classificamos os tipos de descontinuidades que vimos até agora como descontinuidades removíveis, descontinuidades infinitas ou descontinuidades de salto. Intuitivamente, uma descontinuidade removível é uma descontinuidade para a qual há um furo no gráfico, uma descontinuidade de salto é uma descontinuidade não infinita para a qual as seções da função não se encontram e uma descontinuidade infinita é uma descontinuidade localizada em um assíntota vertical. A figura\(\PageIndex{6}\) ilustra as diferenças nesses tipos de descontinuidades. Embora esses termos forneçam uma maneira prática de descrever três tipos comuns de descontinuidades, lembre-se de que nem todas as descontinuidades se encaixam perfeitamente nessas categorias.

Três gráficos, cada um mostrando uma descontinuidade diferente. A primeira é a descontinuidade removível. Aqui, a função dada é uma linha com inclinação positiva. Em um ponto x=a, onde a — Figura\(\PageIndex{6}\): As descontinuidades são classificadas como (a) removíveis, (b) salto ou (c) infinitas.

Essas três descontinuidades são formalmente definidas da seguinte forma:

Definição

Se\(f(x)\) é descontínuo\(a,\) então

1. \(f\)tem uma descontinuidade removível\(a\) quando\(\displaystyle \lim_{x→a}f(x)\) existe. (Nota: Quando afirmamos que\(\displaystyle \lim_{x→a}f(x)\) existe, queremos dizer onde\(L\) está um número real.)\(\displaystyle \lim_{x→a}f(x)=L\)

2. \(f\)tem uma descontinuidade de salto em\(a\) se\(\displaystyle \lim_{x→a^−}f(x)\) e\(\displaystyle \lim_{x→a^+}f(x)\) ambos existem, mas\(\displaystyle \lim_{x→a^−}f(x)≠lim_{x→a^+}f(x)\). (Nota: Quando afirmamos isso\(\displaystyle \lim_{x→a^−}f(x)\) e\(\displaystyle \lim_{x→a^+}f(x)\) ambos existem, queremos dizer que ambos têm valor real e que nenhum deles assume os valores\(±∞\).)

3. \(f\)tem uma descontinuidade infinita em\(a\) if\(\displaystyle \lim_{x→a^−}f(x)=±∞\) ou\(\displaystyle \lim_{x→a^+}f(x)=±∞\).

Exemplo\(\PageIndex{3}\): Classifying a Discontinuity

No exemplo,\(\PageIndex{1A},\) mostramos que\(f(x)=\dfrac{x^2−4}{x−2}\) é descontínuo em\(x=2\). Classifique essa descontinuidade como removível, de salto ou infinita.

Solução

Para classificar a descontinuidade em,\(2\) devemos avaliar\(\displaystyle \lim_{x→2}f(x)\):

\ (\ estilo de exibição\ begin {align*}\ lim_ {x→2} f (x) &=\ lim_ {x→2}\ frac {x^2−4} {x−2}\\ [4pt]
&=\ lim_ {x→2}\ frac {(x−2) (x+2)} {x−2}\\ [4pt]
&=\ lim_ {x→2} (x+2)\\ [4 pontos]
&=4. \ end {align*}\)

Uma vez que\(f\) é descontínuo\(2\) e\(\displaystyle \lim_{x→2}f(x)\) existe,\(f\) tem uma descontinuidade removível em\(x=2\).

Exemplo\(\PageIndex{4}\): Classifying a Discontinuity

No exemplo\(\PageIndex{1B}\), mostramos que\(f(x)=\begin{cases}−x^2+4, &\text{if }x≤3\\4x−8, &\text{if }x>3\end{cases}\) é descontínuo em\(x=3\). Classifique essa descontinuidade como removível, de salto ou infinita.

Solução

Anteriormente, mostramos que\(f\) é descontínuo em\(3\) porque\(\displaystyle \lim_{x→3}f(x)\) não existe. No entanto, uma vez\(\displaystyle \lim_{x→3^−}f(x)=−5\) que\(\displaystyle \lim_{x→3^+}f(x)=4\) ambos existem, concluímos que a função tem uma descontinuidade de salto em\(3\).

Exemplo\(\PageIndex{5}\): Classifying a Discontinuity

Determine se\(f(x)=\dfrac{x+2}{x+1}\) é contínuo em\(−1\). Se a função for descontínua em\(−1\), classifique a descontinuidade como removível, de salto ou infinita.

Solução

O valor da função\(f(−1)\) é indefinido. Portanto, a função não é contínua em\(−1\). Para determinar o tipo de descontinuidade, devemos determinar o limite em\(−1\). Nós vemos isso\(\displaystyle \lim_{x→−1^−}\frac{x+2}{x+1}=−∞\)\(\displaystyle \lim_{x→−1^+}\frac{x+2}{x+1}=+∞\) e. Portanto, a função tem uma descontinuidade infinita em\(−1\).

Exercício\(\PageIndex{3}\)

Pois\(f(x)=\begin{cases}x^2, &\text{if }x≠1\\3, & \text{if }x=1\end{cases}\), decida se\(f\) é contínuo em\(1\). Se não\(f\) for contínuo em\(1\), classifique a descontinuidade como removível, de salto ou infinita.

Dica: Considere as definições dos vários tipos de descontinuidade mencionados acima. Se a função for descontínua em\(1\), veja\(\displaystyle \lim_{x→1}f(x)\)

Resposta: Descontínuo em\(1\); removível

Continuidade ao longo de um intervalo

Agora que exploramos o conceito de continuidade em um determinado momento, estendemos essa ideia à continuidade em um intervalo. À medida que desenvolvemos essa ideia para diferentes tipos de intervalos, pode ser útil ter em mente a ideia intuitiva de que uma função é contínua em um intervalo se pudermos usar um lápis para traçar a função entre quaisquer dois pontos no intervalo sem levantar o lápis do papel. Em preparação para definir a continuidade em um intervalo, começamos examinando a definição do que significa para uma função ser contínua da direita em um ponto e contínua da esquerda em um ponto.

Definição: Continuidade da direita e da esquerda

\(f(x)\)Diz-se que uma função é contínua da direita em\(a\) if\(\displaystyle \lim_{x→a^+}f(x)=f(a)\).

\(f(x)\)Diz-se que uma função é contínua da esquerda em\(a\) if\(\displaystyle \lim_{x→a^−}f(x)=f(a)\)

Uma função é contínua em um intervalo aberto se for contínua em todos os pontos do intervalo. Uma função\(f(x)\) é contínua em um intervalo fechado do formulário\([a,b]\) se for contínua em todos os pontos\((a,b)\) e for contínua da direita em\(a\) e for contínua da esquerda em\(b.\) Analogamente, uma função\(f(x)\) é contínua em um intervalo da forma \((a,b]\)se for contínuo\((a,b)\) e for contínuo da esquerda em\(b.\) Continuidade sobre outros tipos de intervalos são definidos de forma semelhante.

Exigir isso\(\displaystyle \lim_{x→a^+}f(x)=f(a)\) e\(\displaystyle \lim_{x→b^−}f(x)=f(b)\) garante que possamos traçar o gráfico da função de um ponto\((a,f(a))\) a outro\((b,f(b))\) sem levantar o lápis. Se, por exemplo\(\displaystyle \lim_{x→a^+}f(x)≠f(a)\), precisássemos levantar nosso lápis para pular\(f(a)\) para o gráfico do resto da função\((a,b]\).

Exemplo\(\PageIndex{6}\): Continuity on an Interval

Indique o (s) intervalo (s) em que a função\(f(x)=\dfrac{x−1}{x^2+2x}\) é contínua.

Solução

Como\(f(x)=\dfrac{x−1}{x^2+2x}\) é uma função racional, ela é contínua em todos os pontos de seu domínio. O domínio de\(f(x)\) é o conjunto\((−∞,−2)∪(−2,0)∪(0,+∞)\). Assim,\(f(x)\) é contínuo em cada um dos intervalos\((−∞,−2),(−2,0)\),\((0,+∞)\) e.

Exemplo\(\PageIndex{7}\): Continuity over an Interval

Indique o (s) intervalo (s) em que a função\(f(x)=\sqrt{4−x^2}\) é contínua.

Solução

A partir das leis de limite, sabemos que\(\displaystyle \lim_{x→a}\sqrt{4−x^2}=\sqrt{4−a^2}\) para todos os valores de uma polegada\((−2,2)\). Também sabemos que\(\displaystyle \lim_{x→−2^+}\sqrt{4−x^2}=0\) existe e\(\displaystyle \lim_{x→2^−}\sqrt{4−x^2}=0\) existe. Portanto,\(f(x)\) é contínuo ao longo do intervalo\([−2,2]\).

Exercício\(\PageIndex{4}\)

Indique o (s) intervalo (s) em que a função\(f(x)=\sqrt{x+3}\) é contínua.

Dica: Use o exemplo\(\PageIndex{7}\) como guia.

Resposta: \([−3,+∞)\)

O teorema nos\(\PageIndex{2}\) permite expandir nossa capacidade de calcular limites. Em particular, esse teorema, em última análise, nos permite demonstrar que as funções trigonométricas são contínuas em seus domínios.

Teorema\(\PageIndex{2}\): Composite Function Theorem

Se\(f(x)\) for contínuo em\(L\) e\(\displaystyle \lim_{x→a}g(x)=L\), então

\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L).\)

Antes de passarmos para o Exemplo,\(\PageIndex{8},\) lembre-se de que, anteriormente, na seção sobre leis de limites, mostramos\(\displaystyle \lim_{x→0}\cos x=1=\cos(0)\). Consequentemente, sabemos que\(f(x)=\cos x\) é contínuo em\(0\). No exemplo,\(\PageIndex{8},\) vemos como combinar esse resultado com o teorema da função composta.

Exemplo\(\PageIndex{8}\): Limit of a Composite Cosine Function

Avalie\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)\).

Solução

A função dada é uma composição de\(\cos x\)\(x−\frac{π}{2}\) e. Como\(\displaystyle \lim_{x→π/2}\left(x−\frac{π}{2}\right)=0\) e\(\cos x\) é contínuo em\(0\), podemos aplicar o teorema da função composta. Assim,

\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)=\cos\left(\lim_{x→π/2}\left(x−\frac{π}{2}\right)\right)=\cos(0)=1.\)

Exercício\(\PageIndex{4}\):

Avalie\(\displaystyle \lim_{x→π}\sin(x−π)\).

Dica: \(f(x)=\sin x\)é contínuo em\(0\). Use o exemplo\(\PageIndex{8}\) como guia.

Resposta: \(0\)

A prova do próximo teorema usa o teorema da função composta, bem como a continuidade de\(f(x)=\sin x\) e\(g(x)=\cos x\) no ponto\(0\) para mostrar que as funções trigonométricas são contínuas em todos os seus domínios.

Teorema\(\PageIndex{3}\): Continuity of Trigonometric Functions

As funções trigonométricas são contínuas em todos os seus domínios.

Prova

Começamos demonstrando que isso\(\cos x\) é contínuo em cada número real. Para fazer isso, devemos mostrar que,\(\displaystyle \lim_{x→a}\cos x=\cos a\) para todos os valores de\(a\).

\ (\ displaystyle\ begin {align*}\ lim_ {x→a}\ cos x &=\ lim_ {x→a}\ cos ((x−a) +a) & &\ text {Reescrever} x=x−a+a.\\ [4pt]
&=\ lim_ {x→a} (\ cos (x−a)\ cos (x−a)\ cos a−\ sin (x−a)\ sin a) & &\ text {Aplique a identidade para o cosseno da soma de dois ângulos.}\\ [4pt]
&=\ cos (\ lim_ {x→a} (x−a ))\ cos a−\ sin (\ lim_ {x→a} (x−a))\ sin a & &\ text {Desde}\ lim_ {x→a} (x−a) =0,\ text {e}\ sin x\ text {e}\ cos x\ text {são contínuos em} 0.\\ [4pt]
&=\ cos (0)\ − a−\ sin (0))\ sin a & &\ text {Evaluate}\ cos (0)\ text {e}\ sin (0)\ text {e simplifique.}\\ [4pt]
&= 1‣\ cos a −0\ sin a=\ cos a.\ end {align*}\)

A prova que\(\sin x\) é contínua em cada número real é análoga. Como as funções trigonométricas restantes podem ser expressas em termos de\(\sin x\) e\(\cos x\), sua continuidade segue da lei do limite de quociente.

□

Como você pode ver, o teorema da função composta é inestimável para demonstrar a continuidade das funções trigonométricas. À medida que continuamos nosso estudo de cálculo, revisitamos esse teorema muitas vezes.

O teorema do valor intermediário

Funções que são contínuas em intervalos do formulário\([a,b]\), onde\(a\) e\(b\) são números reais, exibem muitas propriedades úteis. Ao longo de nosso estudo de cálculo, encontraremos muitos teoremas poderosos sobre tais funções. O primeiro desses teoremas é o Teorema do Valor Intermediário.

O teorema do valor intermediário

\(f\)Seja contínuo em um intervalo fechado e limitado\([a,b]\). Se\(z\) for qualquer número real entre\(f(a)\) e\(f(b)\), então há um número\([a,b]\) satisfatório\(c\)\(f(c)=z\) na Figura\(\PageIndex{7}\).

Exemplo\(\PageIndex{9}\): Application of the Intermediate Value Theorem

Mostre que\(f(x)=x−\cos x\) tem pelo menos um zero.

Solução

Como\(f(x)=x−\cos x\) é contínuo\((−∞,+∞)\), ele é contínuo em qualquer intervalo fechado do formulário\([a,b]\). Se você puder encontrar um intervalo\([a,b]\) como esse\(f(a)\) e\(f(b)\) tiver sinais opostos, você pode usar o Teorema do Valor Intermediário para concluir que deve haver um número\(c\) real\((a,b)\) que satisfaça\(f(c)=0\). Note que

\(f(0)=0−\cos(0)=−1<0\)

\(f(\frac{π}{2})=\frac{π}{2}−\cos\frac{π}{2}=\frac{π}{2}>0\).

Usando o Teorema do Valor Intermediário, podemos ver que deve haver um número\(c\) real\([0,π/2]\) que satisfaça\(f(c)=0\). Portanto,\(f(x)=x−\cos x\) tem pelo menos um zero.

Exemplo\(\PageIndex{10}\): When Can You Apply the Intermediate Value Theorem?

Se\(f(x)\) for contínuo sobre\([0,2],f(0)>0\) e\(f(2)>0\), podemos usar o Teorema do Valor Intermediário para concluir que não\(f(x)\) tem zeros no intervalo\([0,2]\)? Explique.

Solução

Não. O Teorema do Valor Intermediário só nos permite concluir que podemos encontrar um valor entre\(f(0)\) e\(f(2)\); não nos permite concluir que não podemos encontrar outros valores. Para ver isso com mais clareza, considere a função\(f(x)=(x−1)^2\). Satisfaz\(f(0)=1>0,f(2)=1>0\),\(f(1)=0\) e.

Exemplo\(\PageIndex{11}\): When Can You Apply the Intermediate Value Theorem?

Para\(f(x)=1/x,f(−1)=−1<0\)\(f(1)=1>0\) e. Podemos concluir que\(f(x)\) tem um zero no intervalo\([−1,1]\)?

Solução

Não. A função não é contínua\([−1,1]\). O Teorema do Valor Intermediário não se aplica aqui.

Exercício\(\PageIndex{5}\)

Mostre que\(f(x)=x^3−x^2−3x+1\) tem um zero no intervalo\([0,1]\).

Dica: Encontre\(f(0)\)\(f(1)\) e. Aplique o teorema do valor intermediário.

Resposta: \(f(0)=1>0,\;f(1)=−2<0;\;f(x)\)termina continuamente\([0,1]\). Deve ter um zero nesse intervalo.

Conceitos chave

Para que uma função seja contínua em um ponto, ela deve ser definida nesse ponto, seu limite deve existir no ponto e o valor da função nesse ponto deve ser igual ao valor do limite naquele ponto.
As descontinuidades podem ser classificadas como removíveis, de salto ou infinitas.
Uma função é contínua em um intervalo aberto se for contínua em todos os pontos do intervalo. É contínuo em um intervalo fechado se for contínuo em todos os pontos de seu interior e contínuo em seus pontos finais.
O teorema da função composta afirma: Se\(f(x)\) é contínuo em L e\(\displaystyle \lim_{x→a}g(x)=L\), então\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L)\).

O Teorema do Valor Intermediário garante que, se uma função for contínua em um intervalo fechado, a função assume todos os valores entre os valores em suas extremidades.

Glossário

continuidade em um ponto: Uma função\(f(x)\) é contínua em um ponto\(a\) se e somente se as três condições a seguir forem satisfeitas: (1)\(f(a)\) é definida, (2)\(\displaystyle \lim_{x→a}f(x)\) existe e (3)\(\displaystyle \lim{x→a}f(x)=f(a)\)

continuidade da esquerda: Uma função é contínua da esquerda em\(b\) if\(\displaystyle \lim_{x→b^−}f(x)=f(b)\)

continuidade da direita: Uma função é contínua da direita em\(a\) if\(\displaystyle \lim_{x→a^+}f(x)=f(a)\)

continuidade em um intervalo: uma função que pode ser traçada com um lápis sem levantar o lápis; uma função é contínua em um intervalo aberto se for contínua em todos os pontos do intervalo; uma função\(f(x)\) é contínua em um intervalo fechado do formulário [\(a,b\)] se for contínua em todos os pontos de (\(a,b\)), e é contínuo da direita para\(a\) e da esquerda em\(b\)

descontinuidade em um ponto: Uma função é descontínua em um ponto ou tem uma descontinuidade em um ponto se não for contínua no ponto

descontinuidade infinita: Uma descontinuidade infinita ocorre em um ponto\(a\) se\(\displaystyle \lim_{x→a^−}f(x)=±∞\) ou\(\displaystyle \lim_{x→a^+}f(x)=±∞\)

Teorema do valor intermediário: \(f\)Seja contínuo em um intervalo limitado fechado [\(a,b\)] se\(z\) houver algum número real entre\(f(a)\) e\(f(b)\), então há um número\(c\) em [\(a,b\)] satisfatório\(f(c)=z\)

descontinuidade do salto: Uma descontinuidade de salto ocorre em um ponto\(a\) se\(\displaystyle \lim_{x→a^−}f(x)\) e\(\displaystyle \lim_{x→a^+}f(x)\) ambos existem, mas\(\displaystyle \lim_{x→a^−}f(x)≠\lim_{x→a^+}f(x)\)

descontinuidade removível: Uma descontinuidade removível ocorre em um ponto,\(a\) se\(f(x)\) é descontínua em\(a\), mas\(\displaystyle \lim_{x→a}f(x)\) existe