Skip to main content
Global

2.3E: Exercícios para a Seção 2.3

  1. Last updated
  2. Save as PDF
  • Page ID
    188637

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 4, use as leis de limite para avaliar cada limite. Justifique cada etapa indicando a (s) lei (s) de limite apropriada (s).

    1)\(\displaystyle \lim_{x→0}\,(4x^2−2x+3)\)

    Resposta

    Use a lei múltipla constante e a lei da diferença:

    \(\displaystyle \lim_{x→0}\,(4x^2−2x+3)=4\lim_{x→0}x^2−2\lim_{x→0}x+\lim_{x→0}3=0 + 0 + 3=3\)

    2)\(\displaystyle \lim_{x→1}\frac{x^3+3x^2+5}{4−7x}\)

    3)\(\displaystyle \lim_{x→−2}\sqrt{x^2−6x+3}\)

    Resposta
    Use a lei raiz:\(\displaystyle \lim_{x→−2}\sqrt{x^2−6x+3}=\sqrt{\lim_{x→−2}(x^2−6x+3)}=\sqrt{19}\)

    4)\(\displaystyle \lim_{x→−1}(9x+1)^2\)

    Nos exercícios 5 a 10, use a substituição direta para avaliar o limite de cada função contínua.

    5)\(\displaystyle \lim_{x→7}x^2\)

    Resposta
    \(\displaystyle \lim_{x→7}x^2\;=\;49\)

    6)\(\displaystyle \lim_{x→−2}(4x^2−1)\)

    7)\(\displaystyle \lim_{x→0}\frac{1}{1+\sin x}\)

    Resposta
    \(\displaystyle \lim_{x→0}\frac{1}{1+\sin x}\;=\;1\)

    8)\(\displaystyle \lim_{x→2}e^{2x−x^2}\)

    9)\(\displaystyle \lim_{x→1}\frac{2−7x}{x+6}\)

    Resposta
    \(\displaystyle \lim_{x→1}\frac{2−7x}{x+6}\;=\;−\frac{5}{7}\)

    10)\(\displaystyle \lim_{x→3}\ln e^{3x}\)

    Nos exercícios 11 a 20, use a substituição direta para mostrar que cada limite leva à forma indeterminada\(0/0\). Em seguida, avalie o limite analiticamente.

    11)\(\displaystyle \lim_{x→4}\frac{x^2−16}{x−4}\)

    Resposta
    \(\displaystyle \text{When }x = 4, \quad\frac{x^2−16}{x−4}=\frac{16−16}{4−4}=\frac{0}{0};\)

    então,\(\displaystyle \lim_{x→4}\frac{x^2−16}{x−4}= \lim_{x→4}\frac{(x+4)(x−4)}{x−4}=\lim_{x→4}(x+4) = 4+4 =8\)

    12)\(\displaystyle \lim_{x→2}\frac{x−2}{x^2−2x}\)

    13)\(\displaystyle \lim_{x→6}\frac{3x−18}{2x−12}\)

    Resposta
    \(\displaystyle \text{When }x = 6, \quad\frac{3x−18}{2x−12}=\frac{18−18}{12−12}=\frac{0}{0};\)

    então,\(\displaystyle \lim_{x→6}\frac{3x−18}{2x− 12}=\lim_{x→6}\frac{3(x−6)}{2(x−6)}=\lim_{x→6}\frac{3}{2}=\frac{3}{2}\)

    14)\(\displaystyle \lim_{h→0}\frac{(1+h)^2−1}{h}\)

    15)\(\displaystyle \lim_{t→9}\frac{t−9}{\sqrt{t}−3}\)

    Resposta
    \(\displaystyle \text{When }t = 9, \quad\frac{t−9}{\sqrt{t}−3}=\frac{9−9}{3−3}=\frac{0}{0};\)

    então,\(\displaystyle \lim_{t→9}\frac{t−9}{\sqrt{t}−3} =\lim_{t→9}\frac{t−9}{\sqrt{t}−3}\frac{\sqrt{t}+3}{\sqrt{t}+3}=\lim_{t→9}\frac{(t−9)(\sqrt{t}+3)}{t - 9}=\lim_{t→9}(\sqrt{t}+3)=\sqrt{9}+3=6\)

    16)\(\displaystyle \lim_{h→0}\frac{\dfrac{1}{a+h}−\dfrac{1}{a}}{h}\), onde\(a\) é uma constante de valor real

    17)\(\displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}\)

    Resposta
    \(\displaystyle \text{When }θ = π, \quad\frac{\sin θ}{\tan θ}=\frac{\sin π}{\tan π}=\frac{0}{0};\)

    então,\(\displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}=\lim_{θ→ π}\frac{\sin θ}{\frac{\sin θ}{\cos θ}}=\lim_{θ→π}\cos θ=\cos π=−1\)

    18)\(\displaystyle \lim_{x→1}\frac{x^3−1}{x^2−1}\)

    19)\(\displaystyle \lim_{x→1/2}\frac{2x^2+3x−2}{2x−1}\)

    Resposta
    \(\displaystyle \text{When }x=1/2, \quad\frac{2x^2+3x−2}{2x−1}=\frac{\frac{1}{2}+\frac{3}{2}−2}{1−1}=\frac{0}{0};\)

    então,\(\displaystyle \lim_{x→ 1/2}\frac{2x^2+3x−2}{2x−1}=\lim_{x→1/2}\frac{(2x−1)(x+2)}{2x−1}=\lim_{x→1/2}(x+2)=\frac{1}{2}+2=\frac{5}{2}\)

    20)\(\displaystyle \lim_{x→−3}\frac{\sqrt{x+4}−1}{x+3}\)

    Nos exercícios 21 a 24, use a substituição direta para obter uma expressão indefinida. Em seguida, use o método usado no Exemplo 9 desta seção para simplificar a função e determinar o limite.

    21)\(\displaystyle \lim_{x→−2^−}\frac{2x^2+7x−4}{x^2+x−2}\)

    Resposta
    \(−∞\)

    22)\(\displaystyle \lim_{x→−2^+}\frac{2x^2+7x−4}{x^2+x−2}\)

    23)\(\displaystyle \lim_{x→1^−}\frac{2x^2+7x−4}{x^2+x−2}\)

    Resposta
    \(−∞\)

    24)\(\displaystyle \lim_{x→1^+}\frac{2x^2+7x−4}{x^2+x−2}\)

    Nos exercícios 25 a 32, suponha que\(\displaystyle \lim_{x→6}f(x)=4,\quad \lim_{x→6}g(x)=9\), \(\displaystyle \lim_{x→6}h(x)=6\)e. Use esses três fatos e as leis de limite para avaliar cada limite.

    25)\(\displaystyle \lim_{x→6}2f(x)g(x)\)

    Resposta
    \(\displaystyle \lim_{x→6}2f(x)g(x)=2\left(\lim_{x→6}f(x)\right)\left(\lim_{x→6}g(x)\right)=2 (4)(9)=72\)

    26)\(\displaystyle \lim_{x→6}\frac{g(x)−1}{f(x)}\)

    27)\(\displaystyle \lim_{x→6}\left(f(x)+\frac{1}{3}g(x)\right)\)

    Resposta
    \(\displaystyle \lim_{x→6}\left(f(x)+\frac{1}{3}g(x)\right)=\lim_{x→6}f(x)+\frac{1}{3}\lim_{x→6}g(x)=4+\frac{1}{3}(9)=7\)

    28)\(\displaystyle \lim_{x→6}\frac{\big(h(x)\big)^3}{2}\)

    29)\(\displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}\)

    Resposta
    \(\displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}=\sqrt{\lim_{x→6}g(x)−\lim_{x→6}f(x)}=\sqrt{9-4}=\sqrt{5}\)

    30)\(\displaystyle \lim_{x→6}x⋅h(x)\)

    31)\(\displaystyle \lim_{x→6}[(x+1)⋅f(x)]\)

    Resposta
    \(\displaystyle \lim_{x→6}[(x+1)f(x)]=\left(\lim_{x→6}(x+1)\right)\left(\lim_{x→6}f(x)\right)=7(4)=28\)

    32)\(\displaystyle \lim_{x→6}(f(x)⋅g(x)−h(x))\)

    [T] Nos exercícios 33 a 35, use uma calculadora para desenhar o gráfico de cada função definida por partes e estude o gráfico para avaliar os limites dados.

    33)\(f(x)=\begin{cases}x^2, & x≤3\\ x+4, & x>3\end{cases}\)

    uma.\(\displaystyle \lim_{x→3^−}f(x)\)

    b.\(\displaystyle \lim_{x→3^+}f(x)\)

    Resposta

    O gráfico de uma função por partes com dois segmentos. A primeira é a parábola x^2, que existe para x<=3. O vértice está na origem, ele se abre para cima e há um círculo fechado na extremidade (3,9). O segundo segmento é a linha x+4, que é uma função linear existente para x 3. Há um círculo aberto em (3, 7) e a inclinação é 1." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_03_202.jpeg">

    a.\(9\); b.\( 7\)

    34)\(g(x)=\begin{cases}x^3−1, & x≤0\\1, & x>0\end{cases}\)

    uma.\(\displaystyle \lim_{x→0^−}g(x)\)

    b.\(\displaystyle \lim_{x→0^+}g(x)\)

    35)\(h(x)=\begin{cases}x^2−2x+1, & x<2\\3−x, & x≥2\end{cases}\)

    uma.\(\displaystyle \lim_{x→2^−}h(x)\)

    b.\(\displaystyle \lim_{x→2^+}h(x)\)

    Nos exercícios 36 a 43, use os gráficos a seguir e as leis de limite para avaliar cada limite.

    Dois gráficos de funções por partes. A parte superior é f (x), que tem dois segmentos lineares. A primeira é uma linha com inclinação negativa existente para x < -3. Ele vai em direção ao ponto (-3,0) em x= -3. O próximo tem inclinação crescente e vai até o ponto (-3, -2) em x=-3. Ela existe para x -3. Outros pontos-chave são (0, 1), (-5,2), (1,2), (-7, 4) e (-9,6). A função inferior por partes tem um segmento linear e um segmento curvo. O segmento linear existe para x < -3 e tem inclinação decrescente. Vai para (-3, -2) em x=-3. O segmento curvo parece ser a metade direita de uma parábola de abertura descendente. Ele vai para o ponto de vértice (-3,2) em x=-3. Ele cruza o eixo y um pouco abaixo de y=-2. Outros pontos-chave são (0, -7/3), (-5,0), (1, -5), (-7, 2) e (-9, 4)." style="width: 456px; height: 935px;" width="456px" height="935px" src="https://math.libretexts.org/@api/dek...02_03_201.jpeg">

    36)\(\displaystyle \lim_{x→−3^+}(f(x)+g(x))\)

    37)\(\displaystyle \lim_{x→−3^−}(f(x)−3g(x))\)

    Resposta
    \(\displaystyle \lim_{x→−3^−}(f(x)−3g(x))=\lim_{x→−3^−}f(x)−3\lim_{x→−3^−}g(x)=0+6=6\)

    38)\(\displaystyle \lim_{x→0}\frac{f(x)g(x)}{3}\)

    39)\(\displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}\)

    Resposta
    \(\displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}=\frac{2+\left(\displaystyle \lim_{x→−5}g(x)\right)}{\displaystyle \lim_{x→−5}f(x)}=\frac{2+0}{2}=1\)

    40)\(\displaystyle \lim_{x→1}(f(x))^2\)

    41)\(\displaystyle \lim_{x→1}\sqrt[3]{f(x)−g(x)}\)

    Resposta
    \(\displaystyle \lim_{x→1}\sqrt[3]{f(x)−g(x)}=\sqrt[3]{\lim_{x→1}f(x)−\lim_{x→1}g(x)}=\sqrt[3]{2+5}=\sqrt[3]{7}\)

    (42)\(\displaystyle \lim_{x→−7}(x⋅g(x))\)

    43)\(\displaystyle \lim_{x→−9}[x⋅f(x)+2⋅g(x)]\)

    Resposta
    \(\displaystyle \lim_{x→−9}(xf(x)+2g(x))=\left(\lim_{x→−9}x\right)\left(\lim_{x→−9}f(x)\right)+2\lim_{x→−9}g(x)=(−9)(6)+2(4)=−46\)

    Para os exercícios 44 a 46, avalie o limite usando o teorema da compressão. Use uma calculadora para representar graficamente\(f(x),\;g(x)\) as funções e\(h(x)\) quando possível.

    44) [T] Verdadeiro ou falso? Se\(2x−1≤g(x)≤x^2−2x+3\), então\(\displaystyle \lim_{x→2}g(x)=0\).

    45) [T]\(\displaystyle \lim_{θ→0}θ^2\cos\left(\frac{1}{θ}\right)\)

    Resposta

    O limite é zero.

    O gráfico de três funções sobre o domínio [-1,1], colorido em vermelho, verde e azul da seguinte forma: vermelho: theta^2, verde: theta^2 * cos (1/teta) e azul: - (theta^2). As funções vermelha e azul se abrem para cima e para baixo, respectivamente, como parábolas com vértices na origem. A função verde está presa entre as duas.

    46)\(\displaystyle \lim_{x→0}f(x)\), onde\(f(x)=\begin{cases}0, & x\text{ rational}\\ x^2, & x\text{ irrrational}\end{cases}\)

    47) [T] Na física, a magnitude de um campo elétrico gerado por uma carga pontual a uma distância\(r\) no vácuo é governada pela lei de Coulomb:\(E(r)=\dfrac{q}{4πε_0r^2}\), onde\(E\) representa a magnitude do campo elétrico,\(q\) é a carga da partícula,\(r\) é a distância entre o partícula e onde a força do campo é medida, e\(\dfrac{1}{4πε_0}\) é a constante de Coulomb:\(8.988×109N⋅m^2/C^2\).

    a. Use uma calculadora gráfica para representar graficamente\(E(r)\), desde que a carga da partícula seja\(q=10^{−10}\).

    b. Avalie\(\displaystyle \lim_{r→0^+}E(r)\). Qual é o significado físico dessa quantidade? É fisicamente relevante? Por que você está avaliando da direita?

    Resposta

    uma.

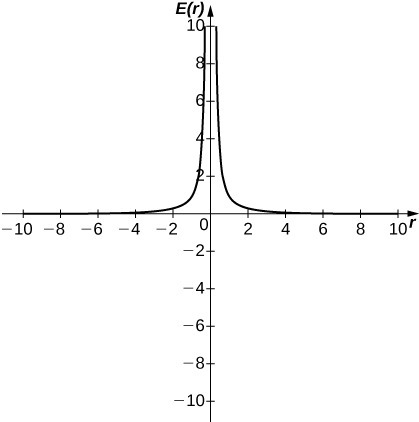
    Um gráfico de uma função com duas curvas. O primeiro está no quadrante dois e se curva assintoticamente para o infinito ao longo do eixo y e para 0 ao longo do eixo x, à medida que x vai para o infinito negativo. O segundo está no quadrante um e se curva assintoticamente para o infinito ao longo do eixo y e para 0 ao longo do eixo x quando x vai para o infinito.

    b. ∞. A magnitude do campo elétrico quando você se aproxima da partícula q se torna infinita. Não faz sentido físico avaliar a distância negativa.

    48) [T] A densidade de um objeto é dada por sua massa dividida por seu volume:\(ρ=m/V.\)

    a. Use uma calculadora para representar graficamente o volume em função da densidade\((V=m/ρ)\), supondo que você esteja examinando algo de massa\(8\) kg (\(m=8\)).

    b. Avalie\(\displaystyle \lim_{x→0^+}V(\rho)\) e explique o significado físico.