2.3: As leis de limite

Last updated
Save as PDF

Page ID: 188618

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

objetivos de aprendizagem

Reconheça as leis básicas de limite.
Use as leis de limite para avaliar o limite de uma função.
Avalie o limite de uma função fatorando.
Use as leis de limite para avaliar o limite de uma função polinomial ou racional.
Avalie o limite de uma função fatorando ou usando conjugados.
Avalie o limite de uma função usando o teorema de compressão.

Na seção anterior, avaliamos os limites examinando gráficos ou construindo uma tabela de valores. Nesta seção, estabelecemos leis para calcular limites e aprendemos como aplicá-las. No Projeto Estudantil no final desta seção, você tem a oportunidade de aplicar essas leis de limite para derivar a fórmula para a área de um círculo, adaptando um método desenvolvido pelo matemático grego Arquimedes. Começamos reafirmando dois resultados de limite úteis da seção anterior. Esses dois resultados, junto com as leis de limites, servem como base para o cálculo de muitos limites.

Avaliando limites com as leis de limites

As duas primeiras leis de limite foram estabelecidas anteriormente e as repetimos aqui. Esses resultados básicos, junto com as outras leis de limite, nos permitem avaliar os limites de muitas funções algébricas.

Limite básico de resultados

Para qualquer número real\(a\) e qualquer constante\(c\),

\(\displaystyle \lim_{x→a}x=a\)
\(\displaystyle \lim_{x→a}c=c\)

Exemplo\(\PageIndex{1}\): Evaluating a Basic Limit

Avalie cada um dos limites a seguir usando “Resultados de limite básicos”.

\(\displaystyle \lim_{x→2}x\)
\(\displaystyle \lim_{x→2}5\)

Solução

O limite de\(x\) conforme\(x\) se\(a\) aproxima é\(a\):\(\displaystyle \lim_{x→2}x=2\).
O limite de uma constante é aquela constante:\(\displaystyle \lim_{x→2}5=5\).

Agora vamos dar uma olhada nas leis de limites, nas propriedades individuais dos limites. As provas que essas leis sustentam são omitidas aqui.

Leis de limite

Deixe\(f(x)\) e\(g(x)\) seja definido para tudo\(x≠a\) em algum intervalo aberto contendo\(a\). \(L\)Suponha que\(M\) sejam números reais como\(\displaystyle \lim_{x→a}f(x)=L\)\(\displaystyle \lim_{x→a}g(x)=M\) e. \(c\)Seja uma constante. Então, cada uma das seguintes afirmações é válida:

Lei de soma para limites:

\[\displaystyle \lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M \nonumber \]

Lei de diferença para limites:

\[\displaystyle \lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M \nonumber \]

Lei múltipla constante para limites:

\[\displaystyle \lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]

Lei de produtos para limites:

\[\displaystyle \lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M \nonumber \]

Lei do quociente para limites:

\[\displaystyle \lim_{x→a}\frac{f(x)}{g(x)}=\frac{\displaystyle \lim_{x→a}f(x)}{\displaystyle \lim_{x→a}g(x)}=\frac{L}{M} \nonumber \]

para\(M≠0\).

Lei de potência para limites:

\[\displaystyle \lim_{x→a}\big(f(x)\big)^n=\big(\lim_{x→a}f(x)\big)^n=L^n \nonumber \]

para cada número inteiro positivo\(n\).

Lei raiz para limites:

\[\displaystyle \lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a} f(x)}=\sqrt[n]{L} \nonumber \]

para todos\(L\),\(n\) é estranho e para\(L≥0\) se\(n\) é par.

Agora praticamos a aplicação dessas leis de limite para avaliar um limite.

Exemplo\(\PageIndex{2A}\): Evaluating a Limit Using Limit Laws

Use as leis de limite para avaliar\[\lim_{x→−3}(4x+2). \nonumber \]

Solução

Vamos aplicar as leis de limite uma etapa de cada vez para ter certeza de que entendemos como elas funcionam. Precisamos ter em mente a exigência de que, em cada aplicação de uma lei de limites, os novos limites devem existir para que a lei de limites seja aplicada.

\[\begin{align*} \lim_{x→−3}(4x+2) &= \lim_{x→−3} 4x + \lim_{x→−3} 2 & & \text{Apply the sum law.}\\[4pt] &= 4⋅\lim_{x→−3} x + \lim_{x→−3} 2 & & \text{Apply the constant multiple law.}\\[4pt] &= 4⋅(−3)+2=−10. & & \text{Apply the basic limit results and simplify.} \end{align*}\]

Exemplo\(\PageIndex{2B}\): Using Limit Laws Repeatedly

Use as leis de limite para avaliar\[\lim_{x→2}\frac{2x^2−3x+1}{x^3+4}. \nonumber \]

Solução

Para encontrar esse limite, precisamos aplicar as leis de limite várias vezes. Novamente, precisamos ter em mente que, ao reescrevermos o limite em termos de outros limites, cada novo limite deve existir para que a lei de limites seja aplicada.

\ [\ begin {align*}\ lim_ {x→2}\ frac {2x^2−3x+1} {x^3+4} &=\ frac {\ displaystyle\ lim_ {x→2} (2x^2−3x+1)} {\ displaystyle\ lim_ {x→2} (x^3+4)} & &\ text {Aplicar a cota lei, certifique-se de que} (2) ^3+4△ 0.\\ [4pt]
&=\ frac {\ displaystyle 2‣\ lim_ {x→2} x^2−3△\ lim_ {x→2} x+\ lim_ {x→2} 1} {\ displaystyle\ lim_ {x→ 2} x^3+\ lim_ {x→2} 4} & &\ text {Aplique a lei da soma e a lei múltipla constante.}\\ [4pt]
&=\ frac {\ displaystyle 2:02\ left (\ lim_ {x→2} x\ right) ^2−3\ lim_ {x→2} x+\ lim_ {x→2} 1} {\ displaystyle\ left (\ lim_ {x→2} x\ right) ^3+\ lim_ {x→2} 4} & &\ text {Aplique a lei de potência.}\\ [4pt]
&=\ frac {2 (4) −3 (2) +1} {(2) ^3+4} =\ frac {1} {4}. & &\ text {Aplique as leis básicas de limite e simplifique.} \ end {align*}\]

Exercício\(\PageIndex{2}\)

Use as leis de limite para avaliar\(\displaystyle \lim_{x→6}(2x−1)\sqrt{x+4}\). Em cada etapa, indique a lei de limite aplicada.

Dica: Comece aplicando a lei do produto.

Responda: \(11\sqrt{10}\)

Limites de funções polinomiais e racionais

Você provavelmente já percebeu que, em cada um dos exemplos anteriores, aconteceu que\(\displaystyle \lim_{x→a}f(x)=f(a)\). Isso nem sempre é verdade, mas vale para todos os polinômios de qualquer escolha de\(a\) e para todas as funções racionais em todos os valores\(a\) para os quais a função racional está definida.

Limites de funções polinomiais e racionais

Seja\(p(x)\) e\(q(x)\) seja funções polinomiais. \(a\)Seja um número real. Então,

\[\lim_{x→a}p(x)=p(a) \nonumber \]

\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)} \nonumber \]

quando\(q(a)≠0\).

Para ver se esse teorema é válido, considere o polinômio

\[p(x)=c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0. \nonumber \]

Ao aplicar as leis de soma, múltiplo constante e potência, acabamos com

\[ \begin{align*} \lim_{x→a}p(x) &= \lim_{x→a}(c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0) \\[4pt] &= c_n\left(\lim_{x→a}x\right)^n+c_{n−1}\left(\lim_{x→a}x\right)^{n−1}+⋯+c_1\left(\lim_{x→a}x\right)+\lim_{x→a}c_0 \\[4pt] &= c_na^n+c_{n−1}a^{n−1}+⋯+c_1a+c_0 \\[4pt] &= p(a) \end{align*}\]

Agora decorre da lei do quociente que se\(p(x)\) e\(q(x)\) são polinômios para os quais\(q(a)≠0\),

depois

\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}. \nonumber \]

Exemplo\(\PageIndex{3}\): Evaluating a Limit of a Rational Function

Avalie\(\displaystyle \lim_{x→3}\frac{2x^2−3x+1}{5x+4}\) o.

Solução

Como 3 está no domínio da função racional\(f(x)=\displaystyle \frac{2x^2−3x+1}{5x+4}\), podemos calcular o limite substituindo 3 por\(x\) na função. Assim,

\[\lim_{x→3}\frac{2x^2−3x+1}{5x+4}=\frac{10}{19}. \nonumber \]

Exercício\(\PageIndex{3}\)

Avalie\(\displaystyle \lim_{x→−2}(3x^3−2x+7)\).

Dica: Use LIMITES DE FUNÇÕES POLINOMIAIS E RACIONAIS como referência

Responda: −13

Técnicas adicionais de avaliação de limites

Como vimos, podemos avaliar facilmente os limites dos polinômios e os limites de algumas (mas não de todas) funções racionais por substituição direta. No entanto, como vimos na seção introdutória sobre limites, certamente é\(\displaystyle \lim_{x→a}f(x)\) possível existir quando\(f(a)\) está indefinido. A observação a seguir nos permite avaliar muitos limites desse tipo:

Se for para todos\(x≠a,\;f(x)=g(x)\) em algum intervalo aberto contendo\(a\), então

\[\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x). \nonumber \]

Para entender melhor essa ideia, considere o limite\(\displaystyle \lim_{x→1}\dfrac{x^2−1}{x−1}\).

A função

\[f(x)=\dfrac{x^2−1}{x−1}=\dfrac{(x−1)(x+1)}{x−1}\nonumber \]

e a função\(g(x)=x+1\) é idêntica para todos os valores de\(x≠1\). Os gráficos dessas duas funções são mostrados na Figura\(\PageIndex{1}\).

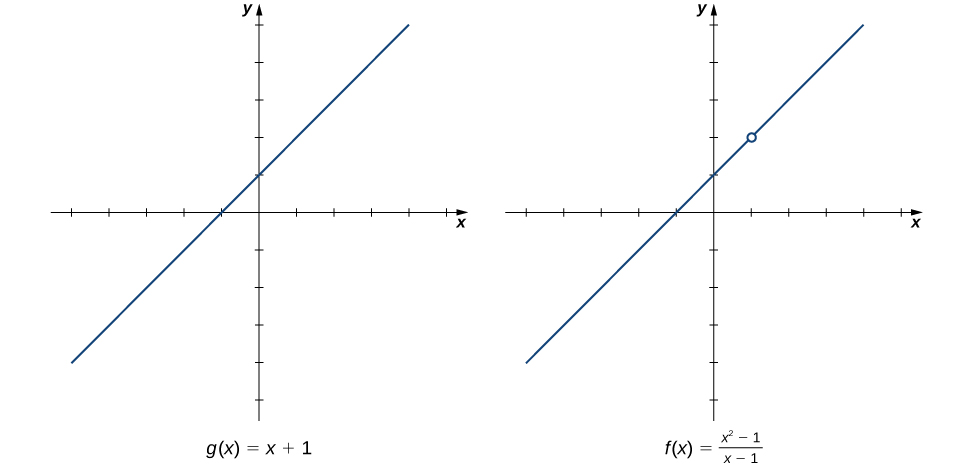
Dois gráficos lado a lado. O primeiro é um gráfico de g (x) = x + 1, uma função linear com intercepto y em (0,1) e intercepto x em (-1,0). O segundo é um gráfico de f (x) = (x^2 — 1)/(x — 1). Este gráfico é idêntico ao primeiro para todos os x, não igual a 1, pois há um círculo aberto em (1,2) no segundo gráfico. — Figura\(\PageIndex{1}\): Os gráficos de\(f(x)\) e\(g(x)\) são idênticos para todos\(x≠1\). Seus limites em 1 são iguais.

Nós vemos isso

\[\lim_{x→1}\dfrac{x^2−1}{x−1}=\lim_{x→1}\dfrac{(x−1)(x+1)}{x−1}=\lim_{x→1}\,(x+1)=2.\nonumber \]

O limite tem a forma\(\displaystyle \lim_{x→a}f(x)/g(x)\), onde\(\displaystyle\lim_{x→a}f(x)=0\)\(\displaystyle\lim_{x→a}g(x)=0\) e. (Nesse caso, dizemos que\(f(x)/g(x)\) tem a forma indeterminada\(0/0\).) A estratégia de resolução de problemas a seguir fornece um esboço geral para avaliar limites desse tipo.

Estratégia de resolução de problemas: calcular um limite quando\(f(x)/g(x)\) has the Indeterminate Form \(0/0\)

Primeiro, precisamos garantir que nossa função tenha a forma apropriada e não possa ser avaliada imediatamente usando as leis de limite.
Em seguida, precisamos encontrar uma função que seja igual a\(h(x)=f(x)/g(x)\) for all\(x≠a\) em algum intervalo contendo a. Para fazer isso, talvez precisemos tentar uma ou mais das seguintes etapas:
1. Se\(f(x)\) e\(g(x)\) forem polinômios, devemos fatorar cada função e cancelar quaisquer fatores comuns.
2. Se o numerador ou denominador contiver uma diferença envolvendo uma raiz quadrada, devemos tentar multiplicar o numerador e o denominador pelo conjugado da expressão envolvendo a raiz quadrada.
3. Se\(f(x)/g(x)\) for uma fração complexa, começamos por simplificá-la.
Por fim, aplicamos as leis de limite.

Os próximos exemplos demonstram o uso dessa estratégia de solução de problemas. O exemplo\(\PageIndex{4}\) ilustra a técnica de fatorar e cancelar; o exemplo\(\PageIndex{5}\) mostra a multiplicação por um conjugado. No exemplo\(\PageIndex{6}\), analisamos a simplificação de uma fração complexa.

Exemplo\(\PageIndex{4}\): Evaluating a Limit by Factoring and Canceling

Avalie\(\displaystyle\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}\).

Solução

Etapa 1. A função\(f(x)=\dfrac{x^2−3x}{2x^2−5x−3}\) é indefinida para\(x=3\). Na verdade, se substituirmos 3 na função que obtemos\(0/0\), que é indefinida. Fatorar e cancelar é uma boa estratégia:

\[\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}=\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}\nonumber \]

Etapa 2. Para todos\(x≠3,\dfrac{x^2−3x}{2x^2−5x−3}=\dfrac{x}{2x+1}\). Portanto,

\[\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}=\lim_{x→3}\dfrac{x}{2x+1}.\nonumber \]

Etapa 3. Avalie usando as leis de limite:

\[\lim_{x→3}\dfrac{x}{2x+1}=\dfrac{3}{7}.\nonumber \]

Exercício\(\PageIndex{4}\)

Avalie\(\displaystyle \lim_{x→−3}\dfrac{x^2+4x+3}{x^2−9}\).

Dica: Siga as etapas da estratégia de solução de problemas

Responda: \(\dfrac{1}{3}\)

Exemplo\(\PageIndex{5}\): Evaluating a Limit by Multiplying by a Conjugate

Avalie\( \displaystyle \lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}\).

Solução

Etapa 1. \( \displaystyle \dfrac{\sqrt{x+2}−1}{x+1}\)tem a forma\(0/0\) em −1. Vamos começar multiplicando por\(\sqrt{x+2}+1\), o conjugado de\(\sqrt{x+2}−1\), no numerador e no denominador:

\[\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}=\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}⋅\dfrac{\sqrt{x+2}+1}{\sqrt{x+2}+1}.\nonumber \]

Etapa 2. Em seguida, multiplicamos o numerador. Não multiplicamos o denominador porque esperamos que o valor\((x+1)\) no denominador seja cancelado no final:

\[=\lim_{x→−1}\dfrac{x+1}{(x+1)(\sqrt{x+2}+1)}.\nonumber \]

Etapa 3. Em seguida, cancelamos:

\[= \lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}.\nonumber \]

Etapa 4. Por fim, aplicamos as leis de limite:

\[\lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}=\dfrac{1}{2}.\nonumber \]

Exercício\(\PageIndex{5}\)

Avalie\( \displaystyle \lim_{x→5}\dfrac{\sqrt{x−1}−2}{x−5}\).

Dica: Siga as etapas da estratégia de solução de problemas

Responda: \(\dfrac{1}{4}\)

Exemplo\(\PageIndex{6}\): Evaluating a Limit by Simplifying a Complex Fraction

Avalie\( \displaystyle \lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\).

Solução

Etapa 1. \(\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\)tem o formulário\(0/0\) em 1. Simplificamos a fração algébrica multiplicando por\(2(x+1)/2(x+1)\):

\[\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}=\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}⋅\dfrac{2(x+1)}{2(x+1)}.\nonumber \]

Etapa 2. Em seguida, multiplicamos por meio dos numeradores. Não multiplique os denominadores porque queremos poder cancelar o fator\((x−1)\):

\[=\lim_{x→1}\dfrac{2−(x+1)}{2(x−1)(x+1)}.\nonumber \]

Etapa 3. Em seguida, simplificamos o numerador:

\[=\lim_{x→1}\dfrac{−x+1}{2(x−1)(x+1)}.\nonumber \]

Etapa 4. Agora, calculamos −1 do numerador:

\[=\lim_{x→1}\dfrac{−(x−1)}{2(x−1)(x+1)}.\nonumber \]

Etapa 5. Em seguida, cancelamos os fatores comuns de\((x−1)\):

\[=\lim_{x→1}\dfrac{−1}{2(x+1)}.\nonumber \]

Etapa 6. Por fim, avaliamos usando as leis de limite:

\[\lim_{x→1}\dfrac{−1}{2(x+1)}=−\dfrac{1}{4}.\nonumber \]

Exercício\(\PageIndex{6}\)

Avalie\( \displaystyle \lim_{x→−3}\dfrac{\dfrac{1}{x+2}+1}{x+3}\).

Dica: Siga as etapas da estratégia de solução de problemas

Responda: −1

\(\PageIndex{7}\)O exemplo não se encaixa perfeitamente em nenhum dos padrões estabelecidos nos exemplos anteriores. No entanto, com um pouco de criatividade, ainda podemos usar essas mesmas técnicas.

Exemplo\(\PageIndex{7}\): Evaluating a Limit When the Limit Laws Do Not Apply

Avalie\( \displaystyle \lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)\).

Solução:

Ambos\(1/x\) e\(5/x(x−5)\) não conseguem ter um limite em zero. Como nenhuma das duas funções tem um limite em zero, não podemos aplicar a lei da soma para limites; devemos usar uma estratégia diferente. Nesse caso, encontramos o limite realizando a adição e aplicando uma de nossas estratégias anteriores. Observe que

\[\dfrac{1}{x}+\dfrac{5}{x(x−5)}=\dfrac{x−5+5}{x(x−5)}=\dfrac{x}{x(x−5)}.\nonumber \]

Assim,

\[\lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)=\lim_{x→0}\dfrac{x}{x(x−5)}=\lim_{x→0}\dfrac{1}{x−5}=−\dfrac{1}{5}.\nonumber \]

Exercício\(\PageIndex{7}\)

Avalie\( \displaystyle \lim_{x→3}\left(\dfrac{1}{x−3}−\dfrac{4}{x^2−2x−3}\right)\).

Dica: Use a mesma técnica do Example\(\PageIndex{7}\). Não se esqueça de considerar\(x^2−2x−3\) antes de obter um denominador comum.

Responda: \(\dfrac{1}{4}\)

Vamos agora rever os limites unilaterais. Modificações simples nas leis de limites nos permitem aplicá-las a limites unilaterais. Por exemplo, para aplicar as leis de limite a um limite do formulário\(\displaystyle \lim_{x→a^−}h(x)\), exigimos que\(h(x)\) a função seja definida em um intervalo aberto do formulário\((b,a)\); para um limite do formulário\(\displaystyle \lim_{x→a^+}h(x)\), exigimos que\(h(x)\) a função seja definida em um intervalo aberto do formulário\((a,c)\). O exemplo\(\PageIndex{8A}\) ilustra esse ponto.

Exemplo\(\PageIndex{8A}\): Evaluating a One-Sided Limit Using the Limit Laws

Avalie cada um dos limites a seguir, se possível.

\(\displaystyle \lim_{x→3^−}\sqrt{x−3}\)
\( \displaystyle \lim_{x→3^+}\sqrt{x−3}\)

Solução

A figura\(\PageIndex{2}\) ilustra a função\(f(x)=\sqrt{x−3}\) e ajuda na nossa compreensão desses limites.

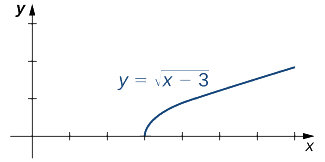
Um gráfico da função f (x) = sqrt (x-3). Visualmente, a função se parece com a metade superior de uma parábola que se abre para a direita com o vértice em (3,0). — Figura\(\PageIndex{2}\): O gráfico mostra a função\(f(x)=\sqrt{x−3}\).

a. A função\(f(x)=\sqrt{x−3}\) é definida ao longo do intervalo\([3,+∞)\). Como essa função não está definida à esquerda de 3, não podemos aplicar as leis de limite para calcular\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\). Na verdade, uma vez que\(f(x)=\sqrt{x−3}\) é indefinido à esquerda de 3,\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\) não existe.

b. Uma vez que\(f(x)=\sqrt{x−3}\) é definido à direita de 3, as leis de limite se aplicam\(\displaystyle\lim_{x→3^+}\sqrt{x−3}\) a. Ao aplicar essas leis de limite, obtemos\(\displaystyle\lim_{x→3^+}\sqrt{x−3}=0\).

No exemplo,\(\PageIndex{8B}\) examinamos os limites unilaterais de uma função definida por partes e usamos esses limites para tirar uma conclusão sobre um limite bilateral da mesma função.

Exemplo\(\PageIndex{8B}\): Evaluating a Two-Sided Limit Using the Limit Laws

Para\(f(x)=\begin{cases}4x−3, & \mathrm{if} \; x<2 \\ (x−3)^2, & \mathrm{if} \; x≥2\end{cases}\), avalie cada um dos seguintes limites:

\(\displaystyle \lim_{x→2^−}f(x)\)
\(\displaystyle \lim_{x→2^+}f(x)\)
\(\displaystyle \lim_{x→2}f(x)\)

Solução

A figura\(\PageIndex{3}\) ilustra a função\(f(x)\) e ajuda na nossa compreensão desses limites.

O gráfico de uma função por partes com dois segmentos. Para x<2, a função é linear com a equação 4x-3. Há um círculo aberto em (2,5). O segundo segmento é uma parábola e existe para x — Figura\(\PageIndex{3}\): Este gráfico mostra uma função\(f(x)\).

a. Uma vez que,\(f(x)=4x−3\) para todos\(x\)\((−∞,2)\),\(f(x)\) substitua o limite por\(4x−3\) e aplique as leis de limite:

\[\lim_{x→2^−}f(x)=\lim_{x→2^−}(4x−3)=5\nonumber \]

b. Uma vez que,\(f(x)=(x−3)^2\) para todos\(x\)\((2,+∞)\),\(f(x)\) substitua o limite por\((x−3)^2\) e aplique as leis de limite:

\[\lim_{x→2^+}f(x)=\lim_{x→2^−}(x−3)^2=1. \nonumber \]

c. Desde\(\displaystyle \lim_{x→2^−}f(x)=5\) e\(\displaystyle \lim_{x→2^+}f(x)=1\), concluímos que isso\(\displaystyle \lim_{x→2}f(x)\) não existe.

Exercício\(\PageIndex{8}\)

Faça um gráfico\(f(x)=\begin{cases}−x−2, & \mathrm{if} \; x<−1\\ 2, & \mathrm{if} \; x=−1 \\ x^3, & \mathrm{if} \; x>−1\end{cases}\) e avalie\(\displaystyle \lim_{x→−1^−}f(x)\).

Dica: Use o método em Exemplo\(\PageIndex{8B}\) para avaliar o limite.

Responda

O gráfico de uma função por partes com três segmentos. A primeira é uma função linear, -x-2, para x<-1. O intercepto x está em (-2,0) e há um círculo aberto em (-1, -1). O próximo segmento é simplesmente o ponto (-1, 2). O terceiro segmento é a função x^3 para x -1, que cruzou o eixo x e o eixo y na origem." src="https://math.libretexts.org/@api/dek...02_03_004.jpeg">

\[\lim_{x→−1^−}f(x)=−1\nonumber \]

Agora voltamos nossa atenção para avaliar um limite do formulário\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}\), onde\(\displaystyle \lim_{x→a}f(x)=K\), onde\(K≠0\)\(\displaystyle \lim_{x→a}g(x)=0\) e. Ou seja,\(f(x)/g(x)\) tem o formulário\(K/0,K≠0\) em\(a\).

Exemplo\(\PageIndex{9}\): Evaluating a Limit of the Form \(K/0,\,K≠0\) Using the Limit Laws

Avalie\(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x^2−2x}\).

Solução

Etapa 1. Depois de substituir\(x=2\), vemos que esse limite tem a forma\(−1/0\). Ou seja, à medida que\(x\) se aproxima\(2\) da esquerda, o numerador se aproxima\(−1\); e o denominador se aproxima\(0\). Consequentemente, a magnitude de\(\dfrac{x−3}{x(x−2)} \) se torna infinita. Para ter uma ideia melhor de qual é o limite, precisamos fatorar o denominador:

\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=\lim_{x→2^−}\dfrac{x−3}{x(x−2)} \nonumber \]

Etapa 2. Como\(x−2\) é a única parte do denominador que é zero quando 2 é substituído, então nos separamos\(1/(x−2)\) do resto da função:

\[=\lim_{x→2^−}\dfrac{x−3}{x}⋅\dfrac{1}{x−2} \nonumber \]

Etapa 3. Usando as Leis de Limite, podemos escrever:

\[=\left(\lim_{x→2^−}\dfrac{x−3}{x}\right)\cdot\left(\lim_{x→2^−}\dfrac{1}{x−2}\right). \nonumber \]

Etapa 4. \(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x}=−\dfrac{1}{2}\)\(\displaystyle \lim_{x→2^−}\dfrac{1}{x−2}=−∞\)e. Portanto, o produto de\((x−3)/x\) e\(1/(x−2)\) tem um limite de\(+∞\):

\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=+∞. \nonumber \]

Exercício\(\PageIndex{9}\)

Avalie\(\displaystyle \lim_{x→1}\dfrac{x+2}{(x−1)^2}\).

Solução: Use os métodos do Example\(\PageIndex{9}\).

Responda: \(+∞\)

O teorema de Squeeze

As técnicas que desenvolvemos até agora funcionam muito bem para funções algébricas, mas ainda não conseguimos avaliar os limites de funções trigonométricas muito básicas. O próximo teorema, chamado de teorema de compressão, se mostra muito útil para estabelecer limites trigonométricos básicos. Esse teorema nos permite calcular limites “comprimindo” uma função, com um limite em um ponto\(a\) desconhecido, entre duas funções com um limite conhecido comum em\(a\). A figura\(\PageIndex{4}\) ilustra essa ideia.

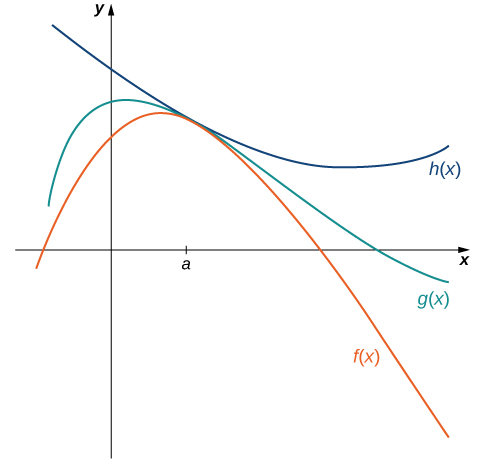
Um gráfico de três funções em um pequeno intervalo. Todas as três funções se curvam. Nesse intervalo, a função g (x) fica presa entre as funções h (x), que fornece maiores valores de y para os mesmos valores de x, e f (x), que fornece valores y menores para os mesmos valores x. Todas as funções se aproximam do mesmo limite quando x=a. — Figura\(\PageIndex{4}\): O Teorema de Squeeze se aplica quando\(f(x)≤g(x)≤h(x)\)\(\displaystyle \lim_{x→a}f(x)=\lim_{x→a}h(x)\) e.

O teorema do aperto

Seja\(f(x),g(x)\), e\(h(x)\) seja definido para tudo\(x≠a\) em um intervalo aberto contendo\(a\). Se

\[f(x)≤g(x)≤h(x) \nonumber \]

para todos\(x≠a\) em um intervalo aberto contendo\(a\) e

\[\lim_{x→a}f(x)=L=\lim_{x→a}h(x) \nonumber \]

onde\(L\) está um número real, então\(\displaystyle \lim_{x→a}g(x)=L.\)

Exemplo\(\PageIndex{10}\): Applying the Squeeze Theorem

Aplique o teorema da compressão para avaliar\(\displaystyle \lim_{x→0} x \cos x\).

Solução

Porque,\(−1≤\cos x≤1\) para todos\(x\), temos\(−x≤x \cos x≤x\) para\(x≥0\) e\(−x≥x \cos x ≥ x\) para\(x≤0\) (se\(x\) for negativo, a direção das desigualdades muda quando multiplicamos). \(\displaystyle \lim_{x→0}(−x)=0=\lim_{x→0}x\)Pois, a partir do teorema da compressão, obtemos\(\displaystyle \lim_{x→0}x \cos x=0\). Os gráficos de\(f(x)=−x,\;g(x)=x\cos x\), e\(h(x)=x\) são mostrados na Figura\(\PageIndex{5}\).

O gráfico de três funções: h (x) = x, f (x) = -x e g (x) = xcos (x). A primeira, h (x) = x, é uma função linear com inclinação de 1 passando pela origem. A segunda, f (x), também é uma função linear com inclinação de −1; passando pela origem. O terceiro, g (x) = xcos (x), se curva entre os dois e passa pela origem. Ele se abre para cima para x — Figura\(\PageIndex{5}\): Os gráficos de\(f(x),\,g(x)\), e\(h(x)\) são mostrados ao redor do ponto\(x=0\).

Exercício\(\PageIndex{10}\)

Use o teorema da compressão para avaliar\(\displaystyle \lim_{x→0}x^2 \sin\dfrac{1}{x}\).

Dica: Use o fato de que\(−x^2≤x^2\sin (1/x) ≤ x^2\) para ajudá-lo a encontrar duas funções que\(x^2\sin (1/x)\) estejam espremidas entre elas.

Responda: 0

Agora usamos o teorema da compressão para abordar vários limites muito importantes. Embora essa discussão seja um pouco longa, esses limites são inestimáveis para o desenvolvimento do material na próxima seção e no próximo capítulo. O primeiro desses limites é\(\displaystyle \lim_{θ→0}\sin θ\). Considere o círculo unitário mostrado na Figura\(\PageIndex{6}\). Na figura, vemos que\(\sin θ\) é a\(y\) coordenada -no círculo unitário e corresponde ao segmento de linha mostrado em azul. A medida radiana do ângulo\(θ\) é o comprimento do arco que ele subtende no círculo unitário. Portanto, vemos que, pois\(0<θ<\dfrac{π}{2},\) temos\(0<\sin θ<θ.\)

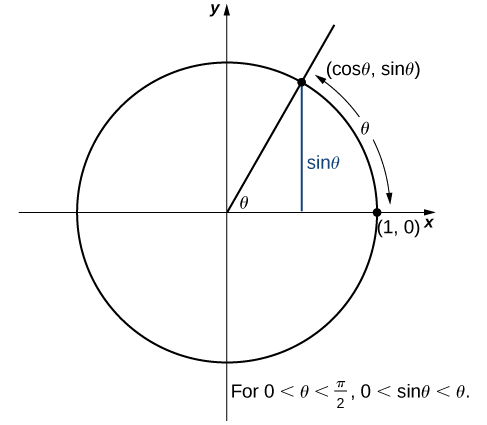
Um diagrama do círculo unitário no plano x, y — é um círculo com raio 1 e centro na origem. Um ponto específico (cos (teta), sin (teta)) é rotulado no quadrante 1 na borda do círculo. Esse ponto é um vértice de um triângulo reto dentro do círculo, com outros vértices na origem e (cos (theta), 0). Assim, os comprimentos dos lados são cos (teta) para a base e sin (teta) para a altura, onde teta é o ângulo criado pela hipotenusa e pela base. A medida radiana do ângulo teta é o comprimento do arco que ele subtende no círculo unitário. O diagrama mostra que para 0 < theta < pi/2, 0 < sin (theta) < teta. — Figura\(\PageIndex{6}\): A função seno é mostrada como uma linha no círculo unitário.

Porque\(\displaystyle \lim_{θ→0^+}0=0\) e\(\displaystyle \lim_{x→0^+}θ=0\), usando o teorema da compressão, concluímos que

\[\lim_{θ→0^+}\sin θ=0.\nonumber \]

Para ver isso\(\displaystyle \lim_{θ→0^−}\sin θ=0\) também, observe isso por\(−\dfrac{π}{2}<θ<0,0<−θ<\dfrac{π}{2}\) e, portanto,\(0<\sin(−θ)<−θ\). Consequentemente,\(0<−\sin θ<−θ\). Daqui resulta isso\(0>\sin θ>θ\). Uma aplicação do teorema da compressão produz o limite desejado. Assim, uma vez que\(\displaystyle \lim_{θ→0^+}\sin θ=0\) e\(\displaystyle \lim_{θ→0^−}\sin θ=0\),

\[\lim_{θ→0}\sin θ=0\nonumber \]

Em seguida, usando a identidade\(\cos θ=\sqrt{1−\sin^2θ}\) para\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\), vemos que

\[\lim_{θ→0}\cos θ=\lim_{θ→0}\sqrt{1−\sin^2θ}=1.\nonumber \]

Agora, examinamos um limite que desempenha um papel importante nos capítulos posteriores, a saber,\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}\). Para avaliar esse limite, usamos o círculo unitário na Figura\(\PageIndex{7}\). Observe que esta figura adiciona um triângulo adicional à Figura\(\PageIndex{6}\). Vemos que o comprimento do lado oposto\(θ\) nesse novo triângulo é\(\tan θ\). Assim, vemos isso para\(0<θ<\dfrac{π}{2}\), nós temos\(\sin θ<θ<\tanθ\).

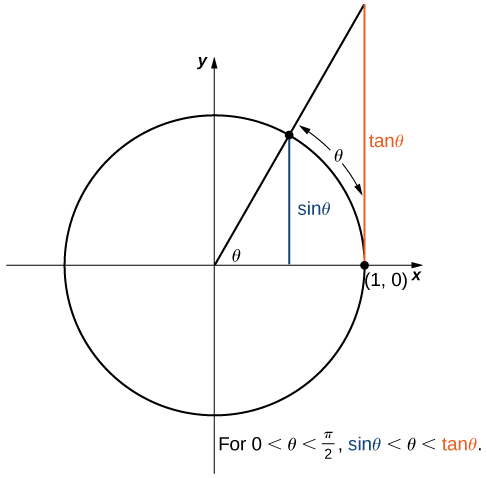
O mesmo diagrama do anterior. No entanto, o triângulo é expandido. A base agora é da origem até (1,0). A altura vai de (1,0) a (1, tan (theta)). A hipotenusa vai da origem até (1, tan (teta)). Como tal, a altura agora é bronzeada (teta). Isso mostra que para 0 < theta < pi/2, sin (theta) < theta < tan (teta). — Figura\(\PageIndex{7}\): As funções seno e tangente são mostradas como linhas no círculo unitário.

Ao dividir por\(\sin θ\) em todas as partes da desigualdade, obtemos

\[1<\dfrac{θ}{\sin θ}<\dfrac{1}{\cos θ}.\nonumber \]

Equivalentemente, temos

\[1>\dfrac{\sin θ}{θ}>\cos θ.\nonumber \]

Desde então\(\displaystyle \lim_{θ→0^+}1=1=\lim_{θ→0^+}\cos θ\), concluímos que\(\displaystyle \lim_{θ→0^+}\dfrac{\sin θ}{θ}=1\), pelo teorema da compressão. Ao aplicar uma manipulação semelhante à usada para demonstrar isso\(\displaystyle \lim_{θ→0^−}\sin θ=0\), podemos mostrar isso\(\displaystyle \lim_{θ→0^−}\dfrac{\sin θ}{θ}=1\). Assim,

\[\lim_{θ→0}\dfrac{\sin θ}{θ}=1. \nonumber \]

No exemplo\(\PageIndex{11}\), usamos esse limite para estabelecer\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0\). Esse limite também se mostra útil em capítulos posteriores.

Exemplo\(\PageIndex{11}\): Evaluating an Important Trigonometric Limit

Avalie\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}\).

Solução

Na primeira etapa, multiplicamos pelo conjugado para que possamos usar uma identidade trigonométrica para converter o cosseno no numerador em um seno:

\ [\ begin {align*}\ lim_ {θ→0}\ dfrac {1−\ cos θ} {θ} &=\ estilo de exibição\ lim_ {θ→0}\ dfrac {1−\ cos θ} {θ},\ dfrac {1+\ cos θ} {1+\ cos θ}\\ [4pt]
&=\ lim_ {θ→0}\ dfrac {1−\ cos^2θ} {θ (1+\ cos θ)}\\ [4pt]
&=\ lim_ {θ→0}\ dfrac {\ sin^2θ} {θ (1+\ cos θ)}\\ [4pt]
&=\ lim_ {θ→0}\ dfrac {\ sin θ } {θ} ‣\ dfrac {\ sin θ} {1+\ cos θ}\\ [4pt]
&=\ left (\ lim_ {θ→0}\ dfrac {\ sin θ} {θ}\ direita)\ cdot\ left (\ lim_ {θ→0}\ dfrac {\ sin θ} {1+\ cos θ}\ direita)\\ [4pt]
= 12\ dfrac {0} {2} =0. \ end {align*}\]

Portanto,

\[\lim_{θ→0}\dfrac{1−\cos θ}{θ}=0. \nonumber \]

Exercício\(\PageIndex{11}\)

Avalie\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{\sin θ}\).

Dica: Multiplique o numerador e o denominador por\(1+\cos θ\).

Responda: 0

Derivando a fórmula para a área de um círculo

Algumas das fórmulas geométricas que consideramos certas hoje foram derivadas pela primeira vez por métodos que antecipam alguns dos métodos de cálculo. O matemático grego Arquimedes (cerca de 287 a 212; a.C.) foi particularmente inventivo, usando polígonos inscritos em círculos para aproximar a área do círculo à medida que o número de lados do polígono aumentava. Ele nunca teve a ideia de um limite, mas podemos usar essa ideia para ver o que suas construções geométricas poderiam ter previsto sobre o limite.

Podemos estimar a área de um círculo computando a área de um polígono regular inscrito. Pense no polígono regular como sendo feito de\(n\) triângulos. Ao considerar o limite conforme o ângulo do vértice desses triângulos vai para zero, você pode obter a área do círculo. Para ver isso, execute as seguintes etapas:

1. Expresse a altura\(h\) e a base\(b\) do triângulo isósceles na Figura\(\PageIndex{8}\) em termos de\(θ\)\(r\) e.

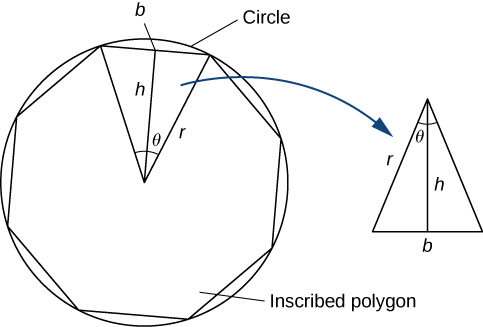
Um diagrama de um círculo com um polígono inscrito — ou seja, um octógono. Um triângulo isósceles é desenhado com um dos lados do octógono como base e o centro do círculo/octógono como vértice superior. A altura h vai do centro da base b até o centro, e cada uma das pernas também é raio r do círculo. O ângulo criado pela altura h e uma das pernas r é rotulado como teta. — Figura\(\PageIndex{8}\)

2. Usando as expressões que você obteve na etapa 1, expresse a área do triângulo isósceles em termos de\(θ\)\(r\) e.

(Substitua\(\frac{1}{2}\sin θ\) por\(\sin\left(\frac{θ}{2}\right)\cos\left(\frac{θ}{2}\right)\) em sua expressão.)

3. Se um polígono regular de\(n\) -face estiver inscrito em um círculo de raio\(r\), encontre uma relação entre\(θ\)\(n\) e. Resolva isso para\(n\). Lembre-se de que há\(2π\) radianos em um círculo. (Use radianos, não graus.)

4. Encontre uma expressão para a área do\(n\) polígono lateral em termos de\(r\)\(θ\) e.

5. Para encontrar uma fórmula para a área do círculo, encontre o limite da expressão na etapa\(θ\) 4 até zero. (Dica:\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}=1)\).

A técnica de estimar áreas de regiões usando polígonos é revisitada em Introdução à Integração.

Conceitos chave

As leis de limite nos permitem avaliar os limites das funções sem precisar passar por processos passo a passo a cada vez.
Para polinômios e funções racionais,\[\lim_{x→a}f(x)=f(a). \nonumber \]
Você pode avaliar o limite de uma função fatorando e cancelando, multiplicando por um conjugado ou simplificando uma fração complexa.
O teorema da compressão permite que você encontre o limite de uma função se a função for sempre maior que uma função e menor que outra função com limites conhecidos.

Equações chave

Limite básico de resultados

\[\lim_{x→a}x=a \quad \quad \lim_{x→a}c=c \nonumber \]

Limites importantes

\[ \lim_{θ→0}\sin θ=0 \nonumber \]

\[ \lim_{θ→0}\cos θ=1 \nonumber \]

\[ \lim_{θ→0}\dfrac{\sin θ}{θ}=1 \nonumber \]

\[ \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0 \nonumber \]

Glossário

lei múltipla constante para limites: a lei de limites\[\lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]

lei de diferença para limites: a lei de limites\[\lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M\nonumber \]

leis de limite: as propriedades individuais dos limites; para cada uma das leis individuais, seja\(f(x)\) e\(g(x)\) seja definido para\(x≠a\) todo o intervalo aberto contendo a; suponha que L e M sejam números reais, de modo que\(\lim_{x→a}f(x)=L\) e\(\lim_{x→a}g(x)=M\); seja c uma constante

lei de potência para limites: a lei limite\[\lim_{x→a}(f(x))^n=(\lim_{x→a}f(x))^n=L^n\nonumber \] para cada número inteiro positivo n

lei de produtos para limites: a lei de limites\[\lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M\nonumber \]

lei do quociente para limites: a lei de limite\(\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{\lim_{x→a}f(x)}{\lim_{x→a}g(x)}=\dfrac{L}{M}\) para M△ 0

lei raiz para limites: a lei limite\(\lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a}f(x)}=\sqrt[n]{L}\) para todo L se n for ímpar e para\(L≥0\) se n for par

teorema de compressão: afirma que se,\(f(x)≤g(x)≤h(x)\) para todos,\(x≠a\) em um intervalo aberto contendo a e\(\lim_{x→a}f(x)=L=\lim_ {x→a}h(x)\) onde L é um número real, então\(\lim_{x→a}g(x)=L\)

lei de soma para limites: A lei de limites\(\lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M\)