2.1: Uma prévia do cálculo

Last updated
Save as PDF

Page ID: 188617

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Descreva o problema da tangente e como ele levou à ideia de uma derivada.
Explique como a ideia de um limite está envolvida na solução do problema da tangente.
Reconheça uma tangente a uma curva em um ponto como o limite das linhas secantes.
Identifique a velocidade instantânea como o limite da velocidade média em um pequeno intervalo de tempo.
Descreva o problema da área e como ele foi resolvido pela integral.
Explique como a ideia de um limite está envolvida na solução do problema da área.
Reconheça como as ideias de limite, derivada e integral levaram aos estudos de séries infinitas e cálculo multivariável.

Ao embarcarmos em nosso estudo de cálculo, veremos como seu desenvolvimento surgiu a partir de soluções comuns para problemas práticos em áreas como a física da engenharia, como o problema de viagens espaciais apresentado na abertura do capítulo. Dois problemas principais levaram à formulação inicial do cálculo: (1) o problema da tangente, ou como determinar a inclinação de uma reta tangente a uma curva em um ponto; e (2) o problema da área, ou como determinar a área sob uma curva.

O problema da tangente e o cálculo diferencial

A taxa de mudança é um dos conceitos mais críticos do cálculo. Começamos nossa investigação das taxas de variação observando os gráficos das três linhas e\(f(x)=−2x−3,\; g(x)=\dfrac{1}{2}x+1\)\(h(x)=2\), mostrados na Figura\(\PageIndex{1}\).

Três gráficos em linha reta. Um, rotulado como “f (x) = -2x - 3", diminui, cruzando o eixo x em -1,5 e o eixo y em -3; outro, rotulado como “g (x) = x/2 + 1”, aumenta, cruzando o eixo x em -2 e o eixo y em 1; o terceiro, rotulado como “h (x) = 2”, é plano na coordenada y 2 — Figura\(\PageIndex{1}\): A taxa de variação de uma função linear é constante em cada um desses três gráficos, com a constante determinada pela inclinação.

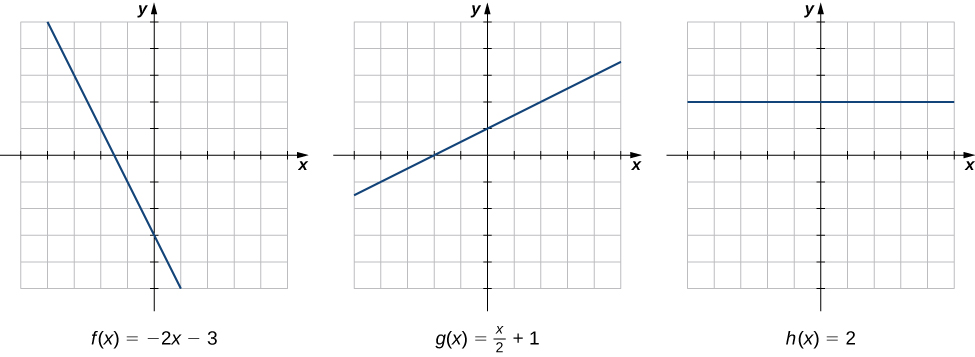
À medida que nos movemos da esquerda para a direita ao longo do gráfico de\(f(x)=−2x−3\), vemos que o gráfico diminui a uma taxa constante. Para cada\(1\) unidade que nos movemos para a direita ao longo do\(x\) eixo\(y\) -, a coordenada -diminui em\(2\) unidades. Essa taxa de mudança é determinada pela inclinação (\(−2\)) da linha. Da mesma forma, a inclinação de\(1/2\) na função nos\(g(x)\) diz que para cada mudança na\(x\)\(1\) unidade há uma mudança correspondente na\(y\)\(1/2\) unidade. A função\(h(x)=2\) tem uma inclinação de zero, indicando que os valores da função permanecem constantes. Vemos que a inclinação de cada função linear indica a taxa de variação da função.

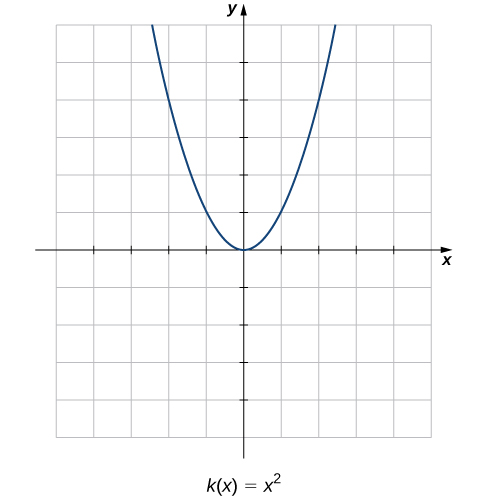
Compare os gráficos dessas três funções com o gráfico de\(k(x)=x^2\) (Figura\(\PageIndex{2}\)). O gráfico de\(k(x)=x^2\) começa da esquerda diminuindo rapidamente, depois começa a diminuir mais lentamente e se nivelar e, finalmente, começa a aumentar — lentamente no início, seguido por uma taxa crescente de aumento à medida que se move em direção à direita. Ao contrário de uma função linear, nenhum número representa a taxa de variação dessa função. Naturalmente, perguntamos: Como medimos a taxa de variação de uma função não linear?

Um gráfico da parábola k (x) = x^2, que se abre e tem seu vértice na origem. — Figura\(\PageIndex{2}\): A função\(k(x)=x^2\) não tem uma taxa de variação constante.

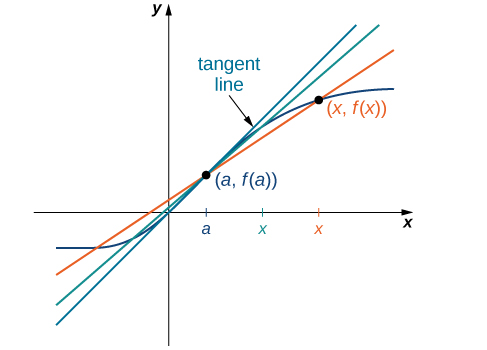
Podemos aproximar a taxa de variação de uma função\(f(x)\) em um ponto\((a,f(a))\) de seu gráfico pegando outro ponto\((x,f(x))\) no gráfico de\(f(x)\), desenhando uma linha através dos dois pontos e calculando a inclinação da linha resultante. Essa linha é chamada de linha secante. A figura\(\PageIndex{3}\) mostra uma linha secante para uma função\(f(x)\) em um ponto\((a,f(a))\).

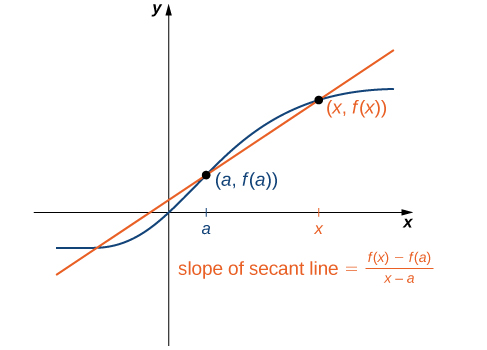
Um gráfico mostrando uma função curva genérica passando pelos pontos (0,0), (a, fa.) e (x, f (x)). Uma linha reta chamada linha secante é traçada através dos pontos (a, fa.) e (x, f (x)), indo abaixo da função curva entre a e x e indo acima da função curva em valores maiores que x ou menores que a. A função curva e a linha secante se cruzam mais uma vez em algum ponto do terceiro quadrante. A inclinação da linha secante é (f (x) — fa.)/(x — a). — Figura\(\PageIndex{3}\): A inclinação de uma linha secante através de um ponto\((a,f(a))\) estima a taxa de variação da função no ponto\((a,f(a))\).

Definimos formalmente uma linha secante da seguinte forma:

Definição: Linha secante

A secante da função\(f(x)\) através dos pontos\((a,f(a))\) e\((x,f(x))\) é a linha que passa por esses pontos. Sua inclinação é dada por

\[m_{sec}=\dfrac{f(x)−f(a)}{x−a}. \label{secantslope} \]

A precisão de aproximar a taxa de mudança da função com uma linha secante depende da proximidade\(x\) de\(a\). Como vemos na Figura\(\PageIndex{4}\), se\(x\) estiver mais perto de\(a\), a inclinação da linha secante é uma medida melhor da taxa de variação de\(f(x)\) at\(a\).

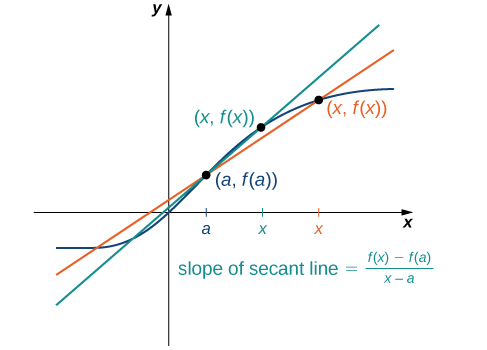
Esse gráfico é o mesmo da linha secante anterior e do gráfico genérico de função curva. No entanto, outro ponto x é adicionado, desta vez traçado mais próximo de a no eixo x. Como tal, outra linha secante é traçada através dos pontos (a, fa.) e a nova, mais próxima (x, f (x)). A linha fica muito mais próxima da função curva genérica ao redor (a, fa.). A inclinação dessa linha secante tornou-se uma melhor aproximação da taxa de mudança da função genérica. — Figura\(\PageIndex{4}\): À medida que\(x\) se aproxima\(a\), a inclinação da linha secante se torna uma melhor aproximação da taxa de mudança da função\(f(x)\) em\(a\).

As próprias linhas secantes se aproximam de uma linha que é chamada de tangente à função\(f(x)\) at\(a\) (Figura\(\PageIndex{5}\)). A inclinação da reta tangente ao gráfico em\(a\) mede a taxa de mudança da função em\(a\). Esse valor também representa a derivada da função\(f(x)\) at\(a\), ou a taxa de variação da função at\(a\). Essa derivada é denotada por\(f′(a)\). O cálculo diferencial é o campo do cálculo relacionado ao estudo das derivadas e suas aplicações.

Este gráfico é uma continuação dos dois anteriores. Desta vez, o gráfico contém a função curva, as duas linhas secantes e uma linha tangente. Quando x se aproxima de a, as linhas secantes se aproximam da reta tangente. — Figura\(\PageIndex{5}\): Resolvendo o problema da tangente: À medida que\(x\) se aproxima\(a\), as linhas secantes se aproximam da reta tangente.

\(\PageIndex{1}\)O exemplo ilustra como encontrar inclinações de linhas secantes. Essas inclinações estimam a inclinação da reta tangente ou, equivalentemente, a taxa de variação da função no ponto em que as inclinações são calculadas.

Exemplo\(\PageIndex{1}\): Finding Slopes of Secant Lines

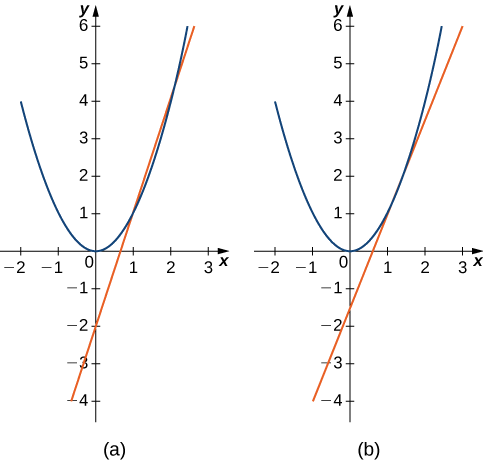
Estime a inclinação da reta tangente (taxa de variação) para\(f(x)=x^2\) at\(x=1\) encontrando inclinações de linhas secantes através\((1,1)\) de cada um dos seguintes pontos no gráfico de\(f(x)=x^2\).

\((2,4)\)
\(\left(\dfrac{3}{2},\dfrac{9}{4}\right)\)

Solução:

Use a fórmula para a inclinação de uma linha secante (Equação\ ref {secantslope}).

\(m_{sec}=\dfrac{4−1}{2−1}=3\)
\(m_{sec}=\dfrac{\dfrac{9}{4}−1}{\dfrac{3}{2}−1}=\dfrac{5}{2}=2.5\)

O ponto na parte b. está mais próximo do ponto\((1,1)\), então a inclinação de\(2.5\) está mais próxima da inclinação da reta tangente. Uma boa estimativa para a inclinação da tangente estaria na faixa de\(2\) até\(2.5\) (Figura\(\PageIndex{6}\)).

Dois gráficos da parábola f (x) = x^2 são mostrados. O primeiro tem uma linha secante traçada, cruzando a parábola em (1,1) e (2,4). A segunda tem uma linha secante traçada, cruzando a parábola em (1,1) e (3/2, 9/4). Essas linhas fornecem aproximações sucessivamente mais próximas da reta tangente à função at (1,1). — Figura\(\PageIndex{6}\): As linhas secantes\((1,1)\) até\(f(x)=x^2\) (a)\((2,4)\) e (b)\((\dfrac{3}{2},\dfrac{9}{4})\) fornecem aproximações sucessivamente mais próximas da reta tangente a\(f(x)=x^2\) at\((1,1)\).

Exercício\(\PageIndex{1}\)

Estime a inclinação da reta tangente (taxa de variação) para\(f(x)=x^2\) at\(x=1\) encontrando as inclinações das linhas secantes\((1,1)\) e o ponto\((\dfrac{5}{4},\dfrac{25}{16})\) no gráfico de\(f(x)=x^2\).

Resposta: \(2.25\)

Continuamos nossa investigação explorando uma questão relacionada. Tendo em mente que a velocidade pode ser considerada como a taxa de mudança de posição, suponha que tenhamos uma função,\(s(t)\), que forneça a posição de um objeto ao longo de um eixo de coordenadas a qualquer momento\(t\). Podemos usar essas mesmas ideias para criar uma definição razoável da velocidade instantânea em um determinado momento?\(t=a?\) Começamos aproximando a velocidade instantânea com uma velocidade média. Primeiro, lembre-se de que a velocidade de um objeto viajando a uma taxa constante é a razão entre a distância percorrida e o tempo que ele percorreu. Definimos a velocidade média de um objeto ao longo de um período de tempo como sendo a mudança em sua posição dividida pela duração do período de tempo.

Definição: Velocidade média

\(s(t)\)Seja a posição de um objeto se movendo ao longo de um eixo de coordenadas ao mesmo tempo\(t\). A velocidade média do objeto em um intervalo de tempo\([a,t]\) onde\(a<t\) (ou\([t,a]\) se\(t<a)\) é

\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \label{avgvel} \]

Conforme\(t\) escolhido mais perto de\(a\), a velocidade média se aproxima da velocidade instantânea. Observe que encontrar a velocidade média de uma função de posição em um intervalo de tempo é essencialmente o mesmo que encontrar a inclinação de uma linha secante em relação a uma função. Além disso, para encontrar a inclinação de uma reta tangente em um ponto\(a\), deixamos que\(x\) os valores -se\(a\) aproximem na inclinação da reta secante. Da mesma forma, para encontrar a velocidade instantânea no momento\(a\), deixamos que\(t\) os valores -se\(a\) aproximem na velocidade média. Esse processo de deixar\(x\) ou\(t\) abordar\(a\) uma expressão é chamado de estabelecimento de um limite. Assim, podemos definir a velocidade instantânea da seguinte forma.

Definição: Velocidade instantânea

Para uma função de posição\(s(t)\), a velocidade instantânea de cada vez\(t=a\) é o valor pelo qual as velocidades médias se aproximam em intervalos da forma\([a,t]\) e à\([t,a]\) medida que os valores de\(t\) se aproximam\(a\), desde que tal valor exista.

\(\PageIndex{2}\)O exemplo ilustra esse conceito de limites e velocidade média.

Exemplo\(\PageIndex{2}\): Finding Average Velocity

Uma pedra é lançada de uma altura de 64 pés. É determinado que sua altura (em pés) acima do solo t segundos depois (para\(0≤t≤2\)) é dada por\(s(t)=−16t^2+64\). Encontre a velocidade média da rocha em cada um dos intervalos de tempo fornecidos. Use essas informações para adivinhar a velocidade instantânea da rocha no momento\(t=0.5\).

[\(0.49,0.5\)]
[\(0.5,0.51\)]

Solução

Substitua os dados na Equação\ ref {avgvel} para definir a velocidade média.

\[v_{ave}=\dfrac{s(0.49)−s(0.5)}{0.49−0.5}=−15.84 \nonumber \]
\[v_{ave}=\dfrac{s(0.51)−s(0.5)}{0.51−0.5}=−16.016 \nonumber \]

A velocidade instantânea está em algum lugar entre −15,84 e −16,16 pés/seg. Uma boa suposição pode ser −16 pés/seg.

Exercício\(\PageIndex{2}\)

Um objeto se move ao longo de um eixo de coordenadas para que sua posição no momento\(t\) seja dada por\(s(t)=t^3\). Estime sua velocidade instantânea no momento\(t=2\) computando sua velocidade média ao longo do intervalo de tempo [\(2,2.001\)].

Dica: Use a Equação\ ref {avgvel} com\(v_{ave}=\dfrac{s(2.001)−s(2)}{2.001−2}\).

Resposta: 12.006001

O problema da área e o cálculo integral

Agora voltamos nossa atenção para uma pergunta clássica do cálculo. Muitas quantidades em física — por exemplo, quantidades de trabalho — podem ser interpretadas como a área sob uma curva. Isso nos leva a fazer a pergunta: Como podemos encontrar a área entre o gráfico de uma função e o\(x\) eixo -em um intervalo (Figura\(\PageIndex{7}\))?

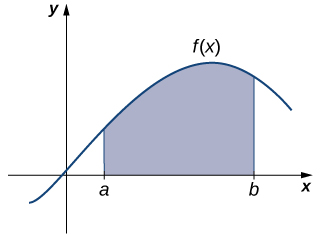
É mostrado um gráfico de uma função curva genérica f (x) em forma de colina no quadrante um. Uma área sob a função é sombreada acima do eixo x e entre x=a e x=b. — Figura\(\PageIndex{7}\): O problema da área: Como encontramos a área da região sombreada?

Como na resposta às nossas perguntas anteriores sobre velocidade, primeiro tentamos aproximar a solução. Aproximamos a área dividindo o intervalo\([a,b]\) em intervalos menores na forma de retângulos. A aproximação da área vem da soma das áreas desses retângulos (Figura\(\PageIndex{8}\)).

O gráfico é o mesmo da imagem anterior, com uma diferença. Em vez da área completamente sombreada sob a função curva, o intervalo [a, b] é dividido em intervalos menores na forma de retângulos. Os retângulos têm a mesma largura pequena. A altura de cada retângulo é a altura da função no ponto médio da base desse retângulo específico. — Figura\(\PageIndex{8}\): A área da região abaixo da curva é aproximada pela soma das áreas de retângulos finos.

À medida que as larguras dos retângulos se tornam menores (se aproximam de zero), a soma das áreas dos retângulos se aproxima da área entre o gráfico de\(f(x)\) e o\(x\) eixo -ao longo do intervalo\([a,b]\). Mais uma vez, nos encontramos atingindo um limite. Limites desse tipo servem como base para a definição da integral definida. O cálculo integral é o estudo das integrais e suas aplicações.

Exemplo\(\PageIndex{3}\): Estimation Using Rectangles

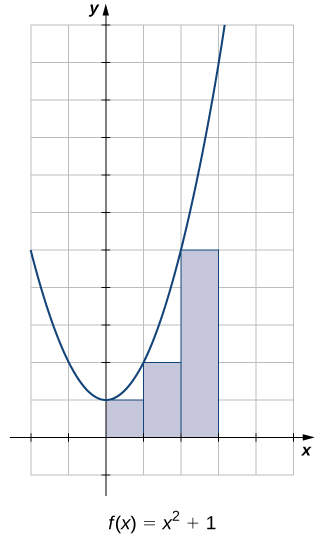
Estime a área entre o\(x\) eixo -e o gráfico do\(f(x)=x^2+1\) intervalo\([0,3]\) usando os três retângulos mostrados na Figura\(\PageIndex{9}\).

Gráfico de uma parábola se abrindo para cima com o ponto mais baixo em (0,1). Um retângulo de altura 1 que se estende de x=0 a x=1 toca a parábola no ponto (0,1); um retângulo de altura 2 de x=1 a x=2 a toca no ponto (1,2); um retângulo de altura 5 de x=2 a x=3 a toca no ponto (2,5) — Figura\(\PageIndex{9}\): A área da região abaixo da curva de\(f(x)=x^2+1\) pode ser estimada usando retângulos.

Solução

As áreas dos três retângulos são 1 unidade ², 2 unidades ² e 5 unidades ². Usando esses retângulos, nossa estimativa de área é de 8 unidades ².

Exercício\(\PageIndex{3}\)

Estime a área entre o\(x\) eixo -e o gráfico do\(f(x)=x^2+1\) intervalo\([0,3]\) usando os três retângulos mostrados na Figura\(\PageIndex{10}\).

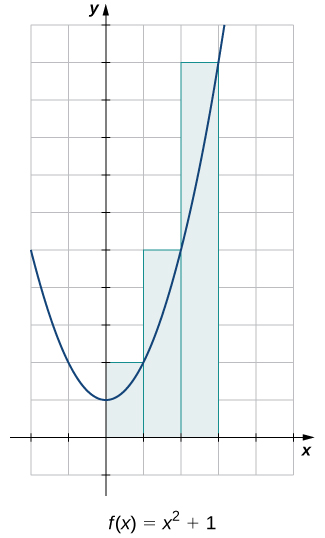
Gráfico de uma parábola se abrindo para cima, com seu ponto mais baixo no ponto (0,1). Um retângulo de altura 2 e que se estende de x=0 a x=1 toca a parábola no ponto (1,2); um retângulo de altura 5 de x=1 a x=2 a toca no ponto (2,5); um retângulo de altura 10 de x=2 a x=3 o toca no ponto (3,10) — Figura\(\PageIndex{10}\): A área da região abaixo da curva de\(f(x)=x^2+1\) pode ser estimada usando retângulos.

Dica: Use o exemplo\(\PageIndex{3}\) como guia

Resposta: 17\(\mathrm{unit}^2\)

Outros aspectos do cálculo

Até agora, estudamos funções de apenas uma variável. Essas funções podem ser representadas visualmente usando gráficos em duas dimensões; no entanto, não há uma boa razão para restringir nossa investigação a duas dimensões. Suponha, por exemplo, que em vez de determinar a velocidade de um objeto se movendo ao longo de um eixo coordenado, desejemos determinar a velocidade de uma rocha disparada de uma catapulta em um determinado momento ou de um avião se movendo em três dimensões. Talvez queiramos representar graficamente funções de valor real de duas variáveis ou determinar volumes de sólidos do tipo mostrado na Figura\(\PageIndex{11}\). Esses são apenas alguns dos tipos de perguntas que podem ser feitas e respondidas usando o cálculo multivariável. Informalmente, o cálculo multivariável pode ser caracterizado como o estudo do cálculo de funções de duas ou mais variáveis. No entanto, antes de explorar essas e outras ideias, devemos primeiro estabelecer uma base para o estudo do cálculo em uma variável, explorando o conceito de limite.

Um diagrama no espaço tridimensional, sobre os eixos x, y e z, onde z = f (x, y). A base é o eixo x, y e a altura é o eixo z. A base é um retângulo contido no plano do eixo x, y. A parte superior é uma superfície de altura variável com cantos localizados diretamente acima dos do retângulo no plano x, y.. O ponto mais alto está acima do canto em x=0, y=0. O ponto mais baixo está na esquina em algum lugar no primeiro quadrante do plano x, y. Os outros dois pontos têm aproximadamente a mesma altura e estão localizados acima dos cantos nos eixos x e y. As linhas são desenhadas conectando os cantos do retângulo aos da superfície. — Figura\(\PageIndex{11}\): Podemos usar o cálculo multivariável para encontrar o volume entre uma superfície definida por uma função de duas variáveis e um plano.

Conceitos chave

O cálculo diferencial surgiu da tentativa de resolver o problema de determinar a inclinação de uma reta tangente a uma curva em um ponto. A inclinação da reta tangente indica a taxa de variação da função, também chamada de derivada. O cálculo de uma derivada requer encontrar um limite.
O cálculo integral surgiu da tentativa de resolver o problema de encontrar a área de uma região entre o gráfico de uma função e o\(x\) eixo. Podemos aproximar a área dividindo-a em retângulos finos e somando as áreas desses retângulos. Essa soma leva ao valor de uma função chamada integral. A integral também é calculada encontrando um limite e, de fato, está relacionada à derivada de uma função.
O cálculo multivariável nos permite resolver problemas no espaço tridimensional, incluindo determinar o movimento no espaço e encontrar volumes de sólidos.

Equações chave

Inclinação de uma linha secante

\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

Velocidade média ao longo do intervalo [a, t]

\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

Glossário

velocidade média: a mudança na posição de um objeto dividida pela duração de um período de tempo; a velocidade média de um objeto em um intervalo de tempo [\(t,a\)] (if\(t<a\) ou [\(a,t\)] if\(t>a\)), com uma posição dada por\(s(t)\), isto é\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

cálculo diferencial: o campo do cálculo preocupado com o estudo das derivadas e suas aplicações

velocidade instantânea: A velocidade instantânea de um objeto com uma função de posição dada por\(s(t)\) é o valor pelo qual as velocidades médias em intervalos de forma [\(t,a\)] e [\(a,t\)] se aproximam à medida que os valores de\(t\) se aproximam\(a\), desde que tal valor exista

cálculo integral: o estudo das integrais e suas aplicações

limite: o processo de permitir que x ou t se aproximem de a em uma expressão; o limite de uma função\(f(x)\) como\(x\) abordagens\(a\) é o valor que\(f(x)\) se aproxima como\(x\) abordagens\(a\)

cálculo multivariável: o estudo do cálculo de funções de duas ou mais variáveis

secante: Uma linha secante para uma função\(f(x)\) em\(a\) é uma linha que passa pelo ponto (\(a,f(a)\)) e outro ponto na função; a inclinação da linha secante é dada por\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

tangente: Uma linha tangente ao gráfico de uma função em um ponto (\(a,f(a)\)) é a linha pela qual as linhas secantes através de (\(a,f(a)\)) se aproximam à medida que são levadas através de pontos na função com\(x\) valores -que se aproximam\(a\); a inclinação da reta tangente a um gráfico\(a\) mede a taxa de mudança de a função em\(a\)