1.5: Funções exponenciais e logarítmicas
- Page ID
- 188602
- Identifique a forma de uma função exponencial.
- Explique a diferença entre os gráficos de\(x^{b}\)\(b^{x}\) e.
- Reconheça a importância do número\(e\).
- Identifique a forma de uma função logarítmica.
- Explique a relação entre as funções exponenciais e logarítmicas.
- Descreva como calcular um logaritmo para uma base diferente.
- Identifique as funções hiperbólicas, seus gráficos e identidades básicas.
Nesta seção, examinamos as funções exponenciais e logarítmicas. Usamos as propriedades dessas funções para resolver equações envolvendo termos exponenciais ou logarítmicos e estudamos o significado e a importância do número\(e\). Também definimos funções hiperbólicas e hiperbólicas inversas, que envolvem combinações de funções exponenciais e logarítmicas. (Observe que apresentamos definições alternativas de funções exponenciais e logarítmicas no capítulo Aplicações de Integrações e provamos que as funções têm as mesmas propriedades com qualquer uma das definições.)
Funções exponenciais
As funções exponenciais surgem em muitas aplicações. Um exemplo comum é o crescimento populacional. Por exemplo, se uma população começa com\(P_0\) indivíduos e depois cresce a uma taxa anual de\(2\%\), sua população após 1 ano é
\[P(1)=P_0+0.02P_0=P_0(1+0.02)=P_0(1.02).\nonumber \]
Sua população após 2 anos é
\[P(2)=P(1)+0.02P(1)=P(1)(1.02)=P_0(1.02)^2.\nonumber \]
Em geral, sua população após\(t\) anos é
\[P(t)=P_0(1.02)^t,\nonumber \]
que é uma função exponencial. De forma mais geral, qualquer função da forma\(f(x)=b^x\), onde\(b>0\),\(b≠1\), é uma função exponencial com base\(b\) e expoente As funções\(x.\) exponenciais têm bases constantes e expoentes variáveis. Observe que uma função da forma\(f(x)=x^b\) para alguma constante não\(b\) é uma função exponencial, mas uma função de potência.
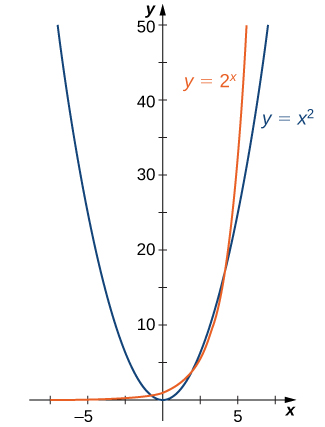
Para ver a diferença entre uma função exponencial e uma função de potência, comparamos as funções\(y=x^2\)\(y=2^x\) e. Na Tabela\(\PageIndex{1}\), vemos que ambos\(2^x\) e nos\(x^2\) aproximamos do infinito como\(x→∞\). Eventualmente, no entanto,\(2^x\) torna-se maior\(x^2\) e cresce mais rapidamente como\(x→∞\). Na direção oposta, como\(x→−∞\)\(x^2→∞\), enquanto\(2^x→0\). A linha\(y=0\) é uma assíntota horizontal para\(y=2^x\).
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(x^2\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| \(2^x\) | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
Na Figura\(\PageIndex{1}\), representamos graficamente os dois\(y=x^2\) e\(y=2^x\) mostramos como os gráficos diferem.
Cálculo de funções exponenciais
Lembre-se das propriedades dos expoentes: Se\(x\) for um número inteiro positivo, definimos\(b^x=b⋅b⋯b\) (com\(x\) fatores de\(b\)). Se\(x\) for um inteiro negativo, então\(x=−y\) para algum inteiro positivo\(y\), e definimos\(b^x=b^{−y}=1/b^y\). Além disso,\(b^0\) é definido como\(1\). Se\(x\) for um número racional, então\(x=p/q\), onde\(p\) e\(q\) são números inteiros\(b^x=b^{p/q}=\sqrt[q]{b^p}\) e. Por exemplo,\(9^{3/2}=\sqrt{9^3}=\left(\sqrt{9}\right)^3=27\). No entanto, como é\(b^x\) definido se\(x\) é um número irracional? Por exemplo, o que queremos dizer com\(2^{\sqrt{2}}\)? Essa é uma pergunta muito complexa para respondermos totalmente agora; no entanto, podemos fazer uma aproximação.
| \(x\) | 1.4 | 1,41 | 1.414 | 1.4142 | 1.41421 | 1.414213 |
|---|---|---|---|---|---|---|
| \(2^x\) | 2.639 | 2.65737 | 2.66475 | 2.65119 | 2.665138 | 2.665143 |
Na Tabela\(\PageIndex{2}\), listamos alguns números racionais que se aproximam\(\sqrt{2}\), e os valores de\(2^x\) para cada número racional também\(x\) são apresentados. Afirmamos que, se escolhermos números\(x\) racionais cada vez mais próximos\(\sqrt{2}\), os valores de\(2^x\) se aproximam cada vez mais de algum número\(L\). Definimos esse número\(L\) como sendo\(2^{\sqrt{2}}\).
Suponha que se saiba que uma determinada população de bactérias dobre de tamanho a cada\(4\) hora. Se uma cultura começa com\(1000\) bactérias, o número de bactérias após o\(4\) expediente é\(n(4)=1000⋅2\). O número de bactérias após o\(8\) expediente é\(n(8)=n(4)⋅2=1000⋅2^2\). Em geral, o número de bactérias após o\(4m\) expediente é\(n(4m)=1000⋅2^m\). Deixando\(t=4m\), vemos que o número de bactérias após t horas é\(n(t)=1000⋅2^{t/4}\). Encontre o número de bactérias após\(6\) horas,\(10\) horas e\(24\) horas.
Solução
O número de bactérias após 6 horas é dado por
\[n(6)=1000⋅2^{6/4}≈2828\, \text{bacteria}. \nonumber \]
O número de bactérias após o\(10\) expediente é dado por
\[n(10)=1000⋅2^{10/4}≈5657\, \text{bacteria}. \nonumber \]
O número de bactérias após o\(24\) expediente é dado pelas\(n(24)=1000⋅2^6=64,000\) bactérias.
Dada a função exponencial\(f(x)=100⋅3^{x/2}\),\(f(4)\) calcule\(f(10)\) e.
- Responda
-
\(f(4)=900\)
\(f(10)=24,300\).
Representação gráfica de funções exponenciais
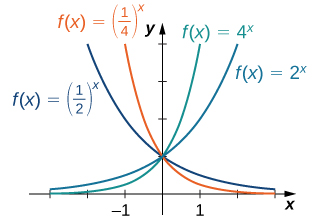
Para qualquer base\(b>0\),\(b≠1\), a função exponencial\(f(x)=b^x\) é definida para todos os números reais\(x\)\(b^x>0\) e. Portanto, o domínio de\(f(x)=b^x\) é\((−∞,∞)\) e o intervalo é\((0,∞)\). Para representar graficamente\(b^x\), notamos que\(b^x\) for\(b>1\), está aumentando em\((−∞,∞)\) e\(b^x→∞\) como\(x→∞\), enquanto\(b^x→0\) as\(x→−∞\). Por outro lado, if\(0<b<1\),\(f(x)=b^x\) está diminuindo em\((−∞,∞)\) e\(b^x→0\) enquanto\(x→∞\)\(b^x→∞\) enquanto\(x→−∞\) (Figura\(\PageIndex{2}\)).
Observe que as funções exponenciais satisfazem as leis gerais dos expoentes. Para lembrá-lo dessas leis, nós as declaramos como regras.
Para quaisquer constantes\(a>0\)\(b>0\), e para todas\(x\) e\(y,\)
- \[b^x⋅b^y=b^{x+y} \nonumber \]
- \[\dfrac{b^x}{b^y}=b^{x−y} \nonumber \]
- \[(b^x)^y=b^{xy} \nonumber \]
- \[(ab)^x=a^xb^x \nonumber \]
- \[\dfrac{a^x}{b^x}=\left(\dfrac{a}{b}\right)^x \nonumber \]
Use as leis dos expoentes para simplificar cada uma das seguintes expressões.
- \(\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}\)
- \(\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}\)
Solução
a. Podemos simplificar da seguinte forma:
\[\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}=\dfrac{2^3(x^{2/3})^3}{4^2(x^{−1/3})^2}= \dfrac{8x^2}{16x^{−2/3}} =\dfrac{x^2x^{2/3}}{2}=\dfrac{x^{8/3}}{2}. \nonumber \]
b. Podemos simplificar da seguinte forma:
\[\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}=\dfrac{(x^3)^2(y^{−1})^2}{x^{−2}(y^2)^{−2}}=\dfrac{x^6y^{−2}}{x^{−2}y^{−4}} =x^6x^2y^{−2}y^4=x^8y^2. \nonumber \]
Use as leis dos expoentes para simplificar\(\dfrac{6x^{−3}y^2}{12x^{−4}y^5}\).
- Dica
-
\(x^a/x^b=x^{a-b}\)
- Responda
-
\(x/(2y^3)\)
O número e
Um tipo especial de função exponencial aparece com frequência em aplicações do mundo real. Para descrevê-lo, considere o seguinte exemplo de crescimento exponencial, que surge da composição de juros em uma conta poupança. Suponha que uma pessoa\(P\) invista dólares em uma conta poupança com uma taxa de juros anual\(r\), composta anualmente. A quantidade de dinheiro após 1 ano é
\(A(1)=P+rP=P(1+r)\).
A quantidade de dinheiro depois de\(2\) anos é
\(A(2)=A(1)+rA(1)=P(1+r)+rP(1+r)=P(1+r)^2\).
De forma mais geral, o valor após\(t\) anos é
\(A(t)=P(1+r)^t\).
Se o dinheiro for composto 2 vezes por ano, a quantia de dinheiro após meio ano é
\(A\left(\dfrac{1}{2}\right)=P+\left(\dfrac{r}{2}\right)P=P\left(1+\left(\dfrac{r}{2}\right)\right)\).
A quantidade de dinheiro após o\(1\) ano é
\(A(1)=A\left(\dfrac{1}{2}\right)+\left(\dfrac{r}{2}\right)A \left(\dfrac{1}{2}\right)=P\left(1+\dfrac{r}{2}\right)+\dfrac{r}{2}\left(\left(P(1+\dfrac{r}{2}\right)\right)=P\left(1+\dfrac{r}{2}\right)^2.\)
Depois de\(t\) anos, a quantidade de dinheiro na conta é
\(A(t)=P\left(1+\dfrac{r}{2}\right)^{2t}\).
De forma mais geral, se o dinheiro for composto\(n\) vezes por ano, a quantia de dinheiro na conta após\(t\) anos é dada pela função
\(A(t)=P\left(1+\dfrac{r}{n}\right)^{nt}.\)
O que acontece?\(n→∞?\) Para responder a essa pergunta, deixamos\(m=n/r\) e escrevemos
\(\left(1+\dfrac{r}{n}\right)^{nt}=\left(1+\dfrac{1}{m}\right)^{mrt},\)
e examine o comportamento de\((1+1/m)^m\) as\(m→∞\), usando uma tabela de valores (Tabela\(\PageIndex{3}\)).
| \(m\) | 10 | 100 | 1000 | 10.000 | 100.000 | 1.000.000 |
|---|---|---|---|---|---|---|
| \(\left(1+\dfrac{1}{m}\right)^m\) | 2.5937 | 2.7048 | 2.7 1692 | 2.7 1815 | 2.7 18268 | 2.718280 |
Olhando para esta tabela, parece que\((1+1/m)^m\) está se aproximando de um número entre\(2.7\) e\(2.8\) como\(m→∞\). De fato,\((1+1/m)^m\) se aproxima de algum número como\(m→∞\). Ligamos para esse número\(e\). Até seis casas decimais de precisão,
\[e≈2.718282. \nonumber \]
A letra\(e\) foi usada pela primeira vez para representar esse número pelo matemático suíço Leonhard Euler durante a década de 1720. Embora Euler não tenha descoberto o número, ele mostrou muitas conexões importantes entre\(e\) as funções logarítmicas. Ainda usamos a notação\(e\) hoje para homenagear o trabalho de Euler porque ela aparece em muitas áreas da matemática e porque podemos usá-la em muitas aplicações práticas.
Voltando ao nosso exemplo de conta poupança, podemos concluir que se uma pessoa coloca\(P\) dólares em uma conta a uma taxa de juros anual\(r\), composta continuamente, então\(A(t)=Pe^{rt}\). Essa função pode ser familiar. Como as funções que envolvem base\(e\) surgem frequentemente em aplicações, chamamos\(f(x)=e^x\) a função de função exponencial natural. Essa função não é apenas interessante por causa da definição do número\(e\), mas também, conforme discutido a seguir, seu gráfico tem uma propriedade importante.
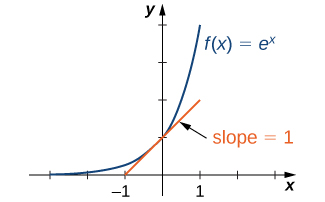
Desde então\(e>1\), sabemos que\(f(x) = e^x\) está aumentando\((−∞,∞)\). Na Figura\(\PageIndex{3}\), mostramos um gráfico de\(f(x)=e^x\) junto com uma reta tangente ao gráfico de\(f\) at\(x=0\). Damos uma definição precisa de reta tangente no próximo capítulo; mas, informalmente, dizemos que uma reta tangente a um gráfico de\(f\) at\(x=a\) é uma linha que passa pelo ponto\((a,f(a))\) e tem a mesma “inclinação” desse\(f\) ponto. A função\(f(x)=e^x\) é a única função exponencial\(b^x\) com linha tangente em\(x=0\) que tem uma inclinação de\(1.\) Como vemos mais adiante no texto, ter essa propriedade torna a função exponencial natural a função exponencial mais simples de usar em muitos casos.
Suponha que\($500\) seja investido em uma conta a uma taxa de juros anual de\(r=5.5\%\), composta continuamente.
- Vamos\(t\) indicar o número de anos após o investimento inicial e\(A(t)\) indicar a quantidade de dinheiro na conta no momento\(t\). Encontre uma fórmula para\(A(t)\).
- Encontre a quantia em dinheiro na conta depois de\(10\) anos e depois de\(20\) anos.
Solução
a. Se os\(P\) dólares forem investidos em uma conta a uma taxa de juros anual\(r\), composta continuamente, então\(A(t)=Pe^{rt}\). Aqui\(P=$500\)\(r=0.055\) e. Portanto,\(A(t)=500e^{0.055t}\).
b. Depois de\(10\) anos, a quantidade de dinheiro na conta é
\(A(10)=500e^{0.055⋅10}=500e^{0.55}≈$866.63\).
Depois de\(20\) anos, a quantidade de dinheiro na conta é
\(A(20)=500e^{0.055⋅20}=500e^{1.1}≈$1,502.08\).
Se\($750\) for investido em uma conta a uma taxa de juros anual de\(4\%\), composta continuamente, encontre uma fórmula para a quantidade de dinheiro na conta após\(t\) anos. Encontre a quantidade de dinheiro depois de\(30\) anos.
- Dica
-
\(A(t)=Pe^{rt}\)
- Responda
-
\(A(t)=750e^{0.04t}\). Depois de\(30\) anos, haverá aproximadamente\($2,490.09\).
Funções logarítmicas
Usando nossa compreensão das funções exponenciais, podemos discutir suas inversas, que são as funções logarítmicas. Eles são úteis quando precisamos considerar qualquer fenômeno que varie em uma ampla faixa de valores, como a escala de pH em química ou decibéis nos níveis de som.
A função exponencial\(f(x)=b^x\) é individual, com domínio\((−∞,∞)\) e alcance\((0,∞)\). Portanto, ele tem uma função inversa, chamada de função logarítmica com base\(b\). Para qualquer um\(b>0,\, b≠1\), a função logarítmica com base\(b\), indicada\(\log_b\), tem domínio\((0,∞)\) e alcance\((−∞,∞)\) e satisfaz
\[\log_b(x)=y \nonumber \]
se e somente se\(b^y=x\).
Por exemplo,
\[\log_2(8)=3\nonumber \]
uma vez que\(2^3=8\),
\[\log_{10}\left(\dfrac{1}{100}\right)=−2 \nonumber \]
uma vez que\(10^{−2}=\dfrac{1}{10^2}=\dfrac{1}{100}\),
\[\log_b(1)=0 \nonumber \]
desde\(b^0=1\) qualquer base\(b>0\).
Além disso, uma vez que\(y=\log_b(x)\) e\(y=b^x\) são funções inversas,
\[\log_b(b^x)=x \nonumber \]
e
\[b^{\log_b(x)}=x. \nonumber \]
A função logarítmica mais usada é a função\(\log_e\). Como essa função usa o natural\(e\) como base, ela é chamada de logaritmo natural. Aqui usamos a notação\(\ln (x)\) ou\(\ln x\) para significar\(\log_e(x)\). Por exemplo,
\[ \begin{align*} \ln (e) &=\log_e(e)=1 \\[4pt] \ln (e^3) &=\log_e(e^3)=3 \\[4pt] \ln (1) &=\log_e(1)=0. \end{align*}\]
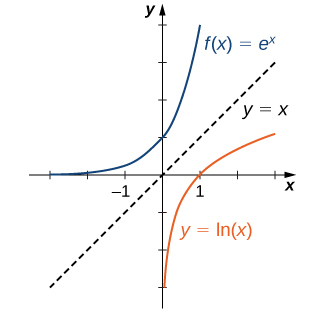
Como as funções\(f(x)=e^x\) e\(g(x)=\ln (x)\) são inversas uma da outra,
\(\ln (e^x)=x\)e\(e^{\ln x}=x\),
e seus gráficos são simétricos em relação à linha\(y=x\) (Figura\(\PageIndex{4}\)).
Em geral, para qualquer base\(b>0\)\(b≠1\), a função\(g(x)=\log_b(x)\) é simétrica em relação à linha\(y=x\) com a função\(f(x)=b^x\). Usando esse fato e os gráficos das funções exponenciais, representamos graficamente funções\(\log_b\) para vários valores de\(b>1\) (Figura\(\PageIndex{5}\)).
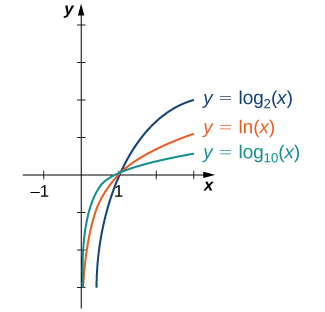
Antes de resolver algumas equações envolvendo funções exponenciais e logarítmicas, vamos revisar as propriedades básicas dos logaritmos.
Se\(a,\,b,\,c>0,\,b≠1\), e\(r\) for qualquer número real, então
- Propriedade do produto
\[\log_b(ac)=\log_b(a)+\log_b(c) \label{productprop} \]
- Propriedade do quociente
\[\log_b \left(\dfrac{a}{c} \right)=\log_b(a)−\log_b(c) \label{quotientprop} \]
- Propriedade de poder
\[\log_b(a^r)=r\log_b(a) \label{powerprop} \]
Resolva cada uma das seguintes equações para\(x\).
- \(5^x=2\)
- \(e^x+6e^{−x}=5\)
Solução
a. Aplicando a função de logaritmo natural em ambos os lados da equação, temos
\(\ln 5^x=\ln 2\).
Usando a propriedade de potência dos logaritmos,
\(x\ln 5=\ln 2.\)
Portanto,
\[x= \dfrac{\ln 2}{\ln 5}. \nonumber \]
b. Multiplicando os dois lados da equação por\(e^x\), chegamos à equação
\(e^{2x}+6=5e^x\).
Reescrevendo essa equação como
\(e^{2x}−5e^x+6=0\),
podemos então reescrevê-la como uma equação quadrática em\(e^x\):
\((e^x)^2−5(e^x)+6=0.\)
Agora podemos resolver a equação quadrática. Fatorando essa equação, obtemos
\((e^x−3)(e^x−2)=0.\)
Portanto, as soluções satisfazem\(e^x=3\)\(e^x=2\) e. Tomar o logaritmo natural de ambos os lados nos dá as soluções\(x=\ln 3,\ln 2\).
Resolver
\[e^{2x}/(3+e^{2x})=1/2. \nonumber \]
- Dica
-
Primeiro resolva a equação para\(e^{2x}\)
- Responda
-
\(x=\dfrac{\ln 3}{2}\).
Resolva cada uma das seguintes equações para\(x\).
- \(\ln \left(\dfrac{1}{x}\right)=4\)
- \(\log_{10}\sqrt{x}+\log_{10}x=2\)
- \(\ln (2x)−3\ln (x^2)=0\)
Solução
a. Pela definição da função logarítmica natural,
\(\ln \left(\dfrac{1}{x} \right)=4\)
- se e somente se\(e^4=\dfrac{1}{x}\).
Portanto, a solução é\(x=1/e^4\).
b. Usando as propriedades de produto (Equação\ ref {productprop}) e potência (Equação\ ref {powerprop}) das funções logarítmicas, reescreva o lado esquerdo da equação como
\[\begin{align*} \log_{10}\sqrt{x} + \log_{10}x &= \log_{10} x \sqrt{x} \\[4pt] &= \log_{10}x^{3/2} \\[4pt] &= \dfrac{3}{2}\log_{10}x. \end{align*}\]
Portanto, a equação pode ser reescrita como
\(\dfrac{3}{2}\log_{10}x=2\)
ou
\(\log_{10}x=\dfrac{4}{3}\).
A solução é\(x=10^{4/3}=10\sqrt[3]{10}\).
c. Usando a propriedade de potência (Equação\ ref {powerprop}) de funções logarítmicas, podemos reescrever a equação como\(\ln (2x)−\ln (x^6)=0\).
Usando a propriedade do quociente (Equation\ ref {quotientprop}), isso se torna
\(\ln \left(\dfrac{2}{x^5}\right)=0\)
Portanto\(2/x^5=1\), o que implica\(x=\sqrt[5]{2}\). Devemos então verificar se há soluções estranhas.
Resolver\(\ln (x^3)−4\ln (x)=1\).
- Dica
-
Primeiro, use a propriedade de potência e, em seguida, use a propriedade do produto dos logaritmos.
- Responda
-
\(x=\dfrac{1}{e}\)
Ao avaliar uma função logarítmica com uma calculadora, você deve ter notado que as únicas opções são\(\log_{10}\) ou\(\log\), chamado de logaritmo comum, ou\(\ln\), que é o logaritmo natural. No entanto, funções exponenciais e funções logarítmicas podem ser expressas em termos de qualquer base desejada\(b\). Se você precisar usar uma calculadora para avaliar uma expressão com uma base diferente, você pode aplicar primeiro as fórmulas de mudança de base. Usando essa mudança de base, normalmente escrevemos uma determinada função exponencial ou logarítmica em termos das funções exponenciais naturais e logarítmicas naturais.
Deixe\(a>0,\,b>0\),\(a≠1,\,b≠1\) e.
1. \(a^x=b^{x \log_ba}\)para qualquer número real\(x\).
Se\(b=e\), essa equação se reduz para\(a^x=e^{x \log_ea}=e^{x \ln a}\).
2. \(\log_ax=\dfrac{\log_bx}{\log_ba}\)para qualquer número real\(x>0\).
Se\(b=e\), essa equação se reduz para\(\log_ax=\dfrac{\ln x}{\ln a}\).
Para a primeira fórmula de mudança de base, começamos fazendo uso da propriedade de potência das funções logarítmicas. Sabemos disso para qualquer base\(b>0,\, b≠1\),\(\log_b(a^x)=x \log_ba\). Portanto,
\(b^{\log_b(a^x)}\)=\(b^{x \log_ba}\).
Além disso, sabemos disso\(b^x\) e\(\log_b(x)\) somos funções inversas. Portanto,
\(b^{\log_b(a^x)}=a^x\).
Combinando essas duas últimas igualdades, concluímos que\(a^x=b^{x \log_ba}\).
Para provar a segunda propriedade, mostramos que
\((\log_ba)⋅(\log_ax)=\log_bx.\)
Deixe\(u=\log_ba,v=\log_ax\),\(w=\log_bx\) e. Vamos mostrar isso\(u⋅v=w\). Pela definição de funções logarítmicas, sabemos disso\(b^u=a,\, a^v=x\),\(b^w=x\) e. A partir das equações anteriores, vemos que
\(b^{uv}=(b^u)^v=a^v=x=b^w.\)
Portanto,\(b^{uv}=b^w\). Como as funções exponenciais são individuais, podemos concluir isso\(u⋅v=w\).
\(\square\)
Use um utilitário de cálculo para avaliar\(\log_37\) com a fórmula de mudança de base apresentada anteriormente.
Solução
Use a segunda equação com\(a=3\) e\(b=e\):\(\log_37=\dfrac{\ln 7}{\ln 3}≈1.77124\).
Use a fórmula de mudança de base e um utilitário de cálculo para avaliar\(\log_46\).
- Dica
-
Use a mudança de base para reescrever essa expressão em termos de expressões envolvendo a função de logaritmo natural.
- Responda
-
\(\log_46 = \dfrac{\ln 6}{\ln 4} \approx 1.29248\)
Em 1935, Charles Richter desenvolveu uma escala (agora conhecida como escala Richter) para medir a magnitude de um terremoto. A escala é uma escala logarítmica de base 10 e pode ser descrita da seguinte forma: Considere um terremoto com magnitude\(R_1\) na escala Richter e um segundo terremoto com magnitude\(R_2\) na escala Richter. Suponha\(R_1>R_2\), o que significa que o terremoto de magnitude\(R_1\) é mais forte, mas quanto mais forte é que o outro terremoto?

Uma forma de medir a intensidade de um terremoto é usar um sismógrafo para medir a amplitude das ondas do terremoto. Se\(A_1\) for a amplitude medida para o primeiro terremoto e\(A_2\) a amplitude medida para o segundo terremoto, então as amplitudes e magnitudes dos dois terremotos satisfazem a seguinte equação:
\(R_1−R_2=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Considere um terremoto que mede 8 na escala Richter e um terremoto que mede 7 na escala Richter. Em seguida,
\(8−7=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Portanto,
\(\log_{10}\left(\dfrac{A1}{A2}\right)=1\),
o que implica\(A_1/A_2=10\) ou\(A_1=10A_2\). Como\(A_1\) tem 10 vezes o tamanho de\(A_2\), dizemos que o primeiro terremoto é 10 vezes mais intenso que o segundo terremoto. Por outro lado, se um terremoto mede 8 na escala Richter e outro mede 6, então a intensidade relativa dos dois terremotos satisfaz a equação
\(\log_{10}\left(\dfrac{A1}{A2}\right)=8−6=2\).
Portanto,\(A_1=100A_2\). Ou seja, o primeiro terremoto é 100 vezes mais intenso que o segundo terremoto.
Como podemos usar funções logarítmicas para comparar a gravidade relativa do terremoto de magnitude 9 no Japão em 2011 com o terremoto de magnitude 7,3 no Haiti em 2010?
Solução
Para comparar os terremotos no Japão e no Haiti, podemos usar uma equação apresentada anteriormente:
\(9−7.3=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Portanto\(A_1/A_2=10^{1.7}\), e concluímos que o terremoto no Japão foi aproximadamente 50 vezes mais intenso do que o terremoto no Haiti.
Compare a gravidade relativa de um\(8.4\) terremoto de magnitude com um\(7.4\) terremoto de magnitude.
- Dica
-
\(R_1−R_2=\log_{10}(A1/A2)\).
- Responda
-
O\(8.4\) terremoto de magnitude é aproximadamente\(10\) duas vezes mais severo que o\(7.4\) terremoto de magnitude.
Funções hiperbólicas
As funções hiperbólicas são definidas em termos de certas combinações de\(e^x\)\(e^{−x}\) e. Essas funções surgem naturalmente em várias aplicações de engenharia e física, incluindo o estudo das ondas de água e das vibrações das membranas elásticas. Outro uso comum de uma função hiperbólica é a representação de uma corrente ou cabo suspenso, também conhecido como catenária (Figura\(\PageIndex{7}\)). Se introduzirmos um sistema de coordenadas para que o ponto baixo da cadeia fique ao longo do\(y\) eixo -, podemos descrever a altura da cadeia em termos de uma função hiperbólica. Primeiro, definimos as funções hiperbólicas.

Cosseno hiperbólico
\(\cosh x=\dfrac{e^x+e^{−x}}{2}\)
Seno hiperbólico
\(\sinh x=\dfrac{e^x−e^{−x}}{2}\)
Tangente hiperbólica
\(\tanh x=\dfrac{\sinh x}{\cosh x}=\dfrac{e^x−e^{−x}}{e^x+e^{−x}}\)
Cossecante hiperbólico
\(\operatorname{csch}x=\dfrac{1}{\sinh x}=\dfrac{2}{e^x−e^{−x}}\)
Secante hiperbólico
\(\operatorname{sech}x=\dfrac{1}{\cosh x}=\dfrac{2}{e^x+e^{−x}}\)
Cotangente hiperbólico
\(\coth x=\dfrac{\cosh x}{\sinh x}=\dfrac{e^x+e^{−x}}{e^x−e^{−x}}\)
O nome\(\cosh\) rima com “caramba”, enquanto o nome\(\sinh\) se pronuncia “cinch”. \(\operatorname{Tanh}, \,\operatorname{sech}, \, \operatorname{csch},\)e\(\coth\) são pronunciados “tanch”, “seech”, “coseech” e “cotanch”, respectivamente.
Usando a definição\(\cosh(x)\) e os princípios da física, pode-se mostrar que a altura de uma corrente suspensa, como a da Figura\(\PageIndex{8}\), pode ser descrita pela função\(h(x)=a\cosh(x/a) + c\) para certas constantes\(a\)\(c\) e.
Mas por que essas funções são chamadas de funções hiperbólicas? Para responder a essa pergunta, considere a quantidade\(\cosh^2 t − \sinh^2 t\). Usando a definição de\(\cosh\) e\(\sinh\), vemos que
\[\cosh^2 t − \sinh^2 t=\dfrac{e^{2t}+2+e^{−2t}}{4}−\dfrac{e^{2t}−2+e^{−2t}}{4}=1. \nonumber \]
Essa identidade é o análogo da identidade trigonométrica\(\cos^2 t + \sin^2 t=1\). Aqui, dado um valor\(t\), o ponto\((x,y)=(\cosh t,\,\sinh t)\) está na hipérbole unitária\(x^2−y^2=1\) (Figura\(\PageIndex{8}\)).
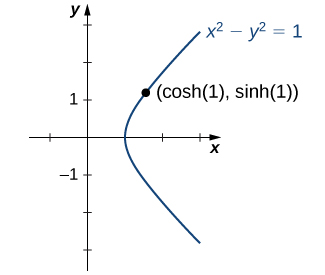
Gráficos de funções hiperbólicas
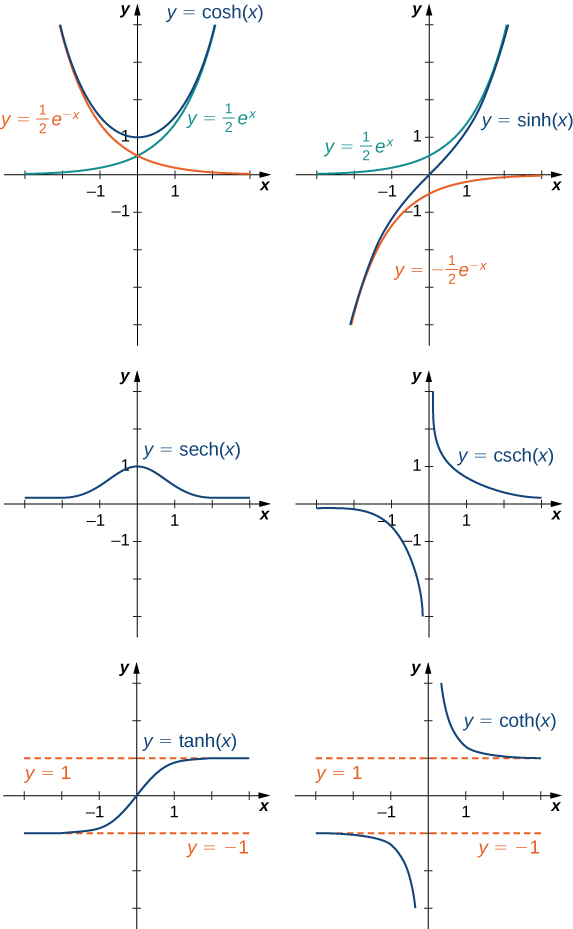
Para representar graficamente\(\cosh x\) e\(\sinh x\), usamos o fato de que ambas as funções se aproximam\((1/2)e^x\) como\(x→∞\), desde\(e^{−x}→0\) as\(x→∞\). Como\(x→−∞,\cosh x\) abordagens\(1/2e^{−x}\), enquanto\(\sinh x\) abordagens\(−1/2e^{−x}\). Portanto, usando os gráficos de\(1/2e^x,1/2e^{−x}\), e\(−1/2e^{−x}\) como guias, graficamos\(\cosh x\)\(\sinh x\) e. Para representar graficamente\(\tanh x\), usamos o fato de que\(\tanh(0)=0\)\(x\),\(−1<\tanh(x)<1\) para todos\(x→∞\),\(\tanh x→1\) como e\(\tanh x→−1\) como\(x→−∞\). Os gráficos das outras três funções hiperbólicas podem ser esboçados usando os gráficos de\(\cosh x\)\(\sinh x\), e\(\tanh x\) (Figura\(\PageIndex{9}\)).
Identidades envolvendo funções hiperbólicas
A identidade\(\cosh^2 t−\sinh^2 t = 1\), mostrada na Figura\(\PageIndex{8}\), é uma das várias identidades que envolvem as funções hiperbólicas, algumas das quais estão listadas a seguir. As primeiras quatro propriedades decorrem facilmente das definições de seno hiperbólico e cosseno hiperbólico. Exceto por algumas diferenças nos sinais, a maioria dessas propriedades é análoga às identidades das funções trigonométricas.
- \(\cosh(−x)=\cosh x\)
- \(\sinh(−x)=−\sinh x\)
- \(\cosh x+\sinh x=e^x\)
- \(\cosh x−\sinh x=e^{−x}\)
- \(\cosh^2 x−\sinh^2 x=1\)
- \(1−\tanh^2 x=\operatorname{sech}^2 x\)
- \(\coth^2 x −1=\operatorname{csch}^2 x\)
- \(\sinh(x±y)=\sinh x \cosh y ± \cosh x \sinh y\)
- \(\cosh(x±y)=\cosh x \cosh y ± \sinh x \sinh y\)
- Simplifique\(\sinh(5\ln x)\).
- Se\(\sinh x=3/4\), encontre os valores das cinco funções hiperbólicas restantes.
Solução:
a. Usando a definição da\(\sinh\) função, escrevemos
\(\sinh(5\ln x)=\dfrac{e^{5\ln x}−e^{−5\ln x}}{2}=\dfrac{e^{\ln (x^5)}−e^{\ln (x^{−5})}}{2}=\dfrac{x^5−x^{−5}}{2}.\)
b. Usando a identidade\(\cosh^2 x − \sinh^2 x=1\), vemos que
\(\cosh^2 x=1+\left(\frac{3}{4}\right)^2=\dfrac{25}{16}.\)
Já que,\(\cosh x≥1\) para todos\(x\), devemos ter\(\cosh x=5/4\). Então, usando as definições para as outras funções hiperbólicas, concluímos que\(\tanh x=3/5,\operatorname{csch}x=4/3,\operatorname{sech}x=4/5\),\(\coth x=5/3\) e.
Simplifique\(\cosh(2\ln x)\).
- Dica
-
Use a definição da\(\cosh\) função e a propriedade de potência das funções logarítmicas.
- Responda
-
\((x^2+x^{−2})/2\)
Funções hiperbólicas inversas
A partir dos gráficos das funções hiperbólicas, vemos que todas elas são individuais, exceto\(\cosh x\)\(\operatorname{sech}x\) e. Se restringirmos os domínios dessas duas funções ao intervalo\([0,∞),\), todas as funções hiperbólicas serão individuais e poderemos definir as funções hiperbólicas inversas. Como as próprias funções hiperbólicas envolvem funções exponenciais, as funções hiperbólicas inversas envolvem funções logarítmicas.
\ [\ begin {align*} &\ sinh^ {−1} x =\ operatorname {arcsinh} x=\ ln\ left (x+\ sqrt {x^2+1}\ direita) &\ cosh^ {−1} x =\ operatorname {arccosh} x=\ ln\ left (x+\ sqrt {x^2−1}\ direita)\\ [4pt]
&\ tanh^ {−1} x=\ operatorname {arctanh} x=\ dfrac {1} {2}\ ln\ left (\ dfrac {1+x} {1−x}\ direita) & &\ coth^ {−1} x =\ nome do operador {arccot} x=\ frac {1} {2}\ ln\ left (\ dfrac {x+1} {x−1}\ direita)\\ [4pt]
&\ operatorname {sech} ^ {−1} x=\ operatorname {arcsech} x=\ ln\ left (\ dfrac {1+\ sqrt {1−x^2} {x}\ right) & &\ operatorname {csch} ^ {−1} x=\ operatorname {arccsch} x=\ ln\ left (\ dfrac {1} {x} +\ dfrac {\ sqrt {1+x^2}} {|x|}\ direita)\ end { alinhamento*}\]
Vamos ver como derivar a primeira equação. Os outros seguem da mesma forma. Suponha\(y=\sinh^{−1}x\). Então,\(x=\sinh y\) e, pela definição da função senoidal hiperbólica,\(x=\dfrac{e^y−e^{−y}}{2}\). Portanto,
\(e^y−2x−e^{−y}=0.\)
Multiplicando essa equação por\(e^y\), obtemos
\(e^{2y}−2xe^y−1=0\).
Isso pode ser resolvido como uma equação quadrática, com a solução
\(e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}=x±\sqrt{x^2+1}\).
Pois\(e^y>0\), a única solução é aquela com sinal positivo. Aplicando o logaritmo natural aos dois lados da equação, concluímos que
\(y=\ln (x+\sqrt{x^2+1}).\)
Avalie cada uma das expressões a seguir.
\(\sinh^{−1}(2)\)
\(\tanh^{−1}(1/4)\)
Solução:
\[\sinh^{−1}(2)=\ln (2+\sqrt{2^2+1})=\ln (2+\sqrt{5})≈1.4436\nonumber \]
\[\tanh^{−1}(1/4)=\frac{1}{2}\ln \left(\dfrac{1+1/4}{1−1/4}\right)=\frac{1}{2}\ln \left(\dfrac{5/4}{3/4}\right)=\frac{1}{2}\ln \left(\dfrac{5}{3}\right)≈0.2554\nonumber \]
Avalie\(\tanh^{−1}(1/2)\).
- Dica
-
Use a definição\(\tanh^{−1}x\) e simplifique.
- Responda
-
\(\dfrac{1}{2}\ln (3)≈0.5493\).
Conceitos-chave
- A função exponencial\(y=b^x\) está aumentando if\(b>1\) e diminuindo if\(0<b<1\). Seu domínio é\((−∞,∞)\) e seu alcance é\((0,∞)\).
- A função logarítmica\(y=\log_b(x)\) é o inverso de\(y=b^x\). Seu domínio é\((0,∞)\) e seu alcance é\((−∞,∞).\)
- A função exponencial natural é\(y=e^x\) e a função logarítmica natural é\(y=\ln x=\log_ex.\)
- Dada uma função exponencial ou função logarítmica na base\(a\), podemos fazer uma mudança de base para converter essa função em qualquer base\(b>0\). Normalmente\(b≠1.\) convertemos em base\(e\).
- As funções hiperbólicas envolvem combinações das funções exponenciais\(e^x\) e,\(e^{−x}.\) como resultado, as funções hiperbólicas inversas envolvem o logaritmo natural.
Glossário
- base
- o número\(b\) na função exponencial\(f(x)=b^x\) e a função logarítmica\(f(x)=\log_bx\)
- expoente
- o valor\(x\) na expressão\(b^x\)
- funções hiperbólicas
- as funções denotadas\(\sinh,\,\cosh,\,\operatorname{tanh},\,\operatorname{csch},\,\operatorname{sech},\) e\(\coth\), que envolvem certas combinações de\(e^x\) e\(e^{−x}\)
- funções hiperbólicas inversas
- os inversos das funções hiperbólicas onde\(\cosh\) e\( \operatorname{sech}\) estão restritos ao domínio\([0,∞)\); cada uma dessas funções pode ser expressa em termos de uma composição da função logarítmica natural e uma função algébrica
- função exponencial natural
- a função\(f(x)=e^x\)
- logaritmo natural
- a função\(\ln x=\log_ex\)
- número e
- à\(m\) medida que aumenta, a quantidade\((1+(1/m)^m\) se aproxima de algum número real; definimos que o número real seja\(e;\) o valor de\(e\) aproximadamente\(2.718282\)


